Suppose this distribution represents the probabilities of

Last updated: 10/24/2023

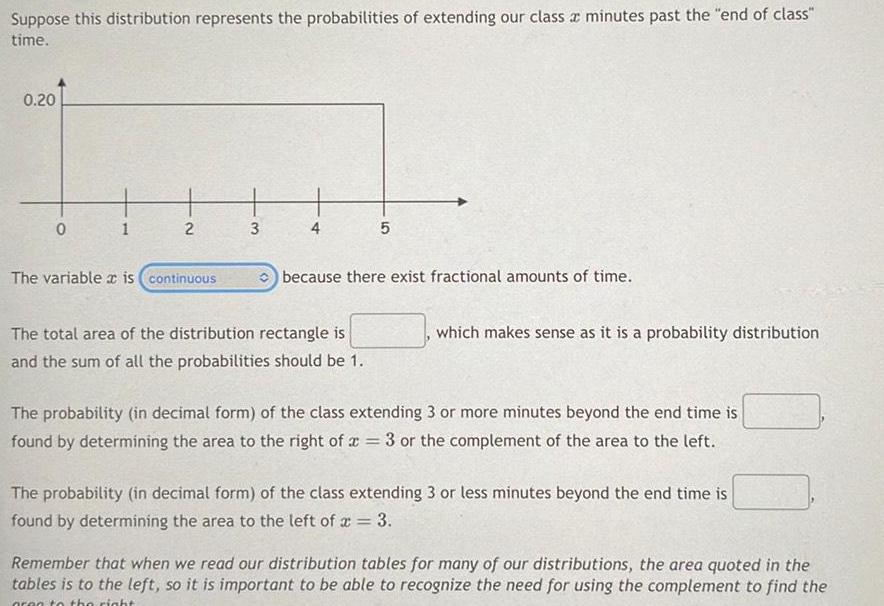
Suppose this distribution represents the probabilities of extending our class a minutes past the end of class time 0 20 0 1 2 The variable is continuous 3 4 5 because there exist fractional amounts of time The total area of the distribution rectangle is and the sum of all the probabilities should be 1 which makes sense as it is a probability distribution The probability in decimal form of the class extending 3 or more minutes beyond the end time is found by determining the area to the right of a 3 or the complement of the area to the left The probability in decimal form of the class extending 3 or less minutes beyond the end time is found by determining the area to the left of x 3 Remember that when we read our distribution tables for many of our distributions the area quoted in the tables is to the left so it is important to be able to recognize the need for using the complement to find the area to the right