The moment generating function of the random variable X

Last updated: 6/29/2023

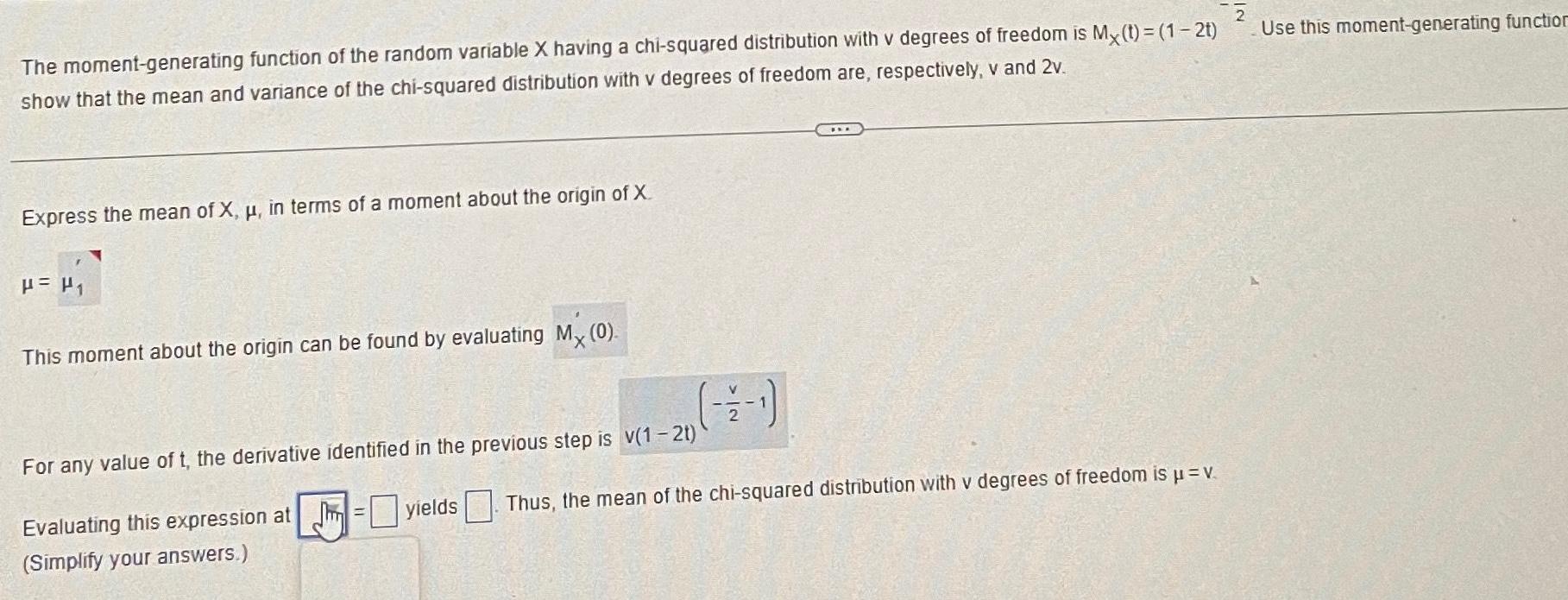
The moment generating function of the random variable X having a chi squared distribution with v degrees of freedom is Mx t 1 2t show that the mean and variance of the chi squared distribution with v degrees of freedom are respectively v and 2v Express the mean of X u in terms of a moment about the origin of X P This moment about the origin can be found by evaluating My 0 For any value of t the derivative identified in the previous step is v 1 2t Evaluating this expression at Simplify your answers yields Thus the mean of the chi squared distribution with v degrees of freedom is v Use this moment generating function