The solutions x y of the equation x2 16y2 16 form an ellipse as pictured below Consider the point P as pictured with x

Question

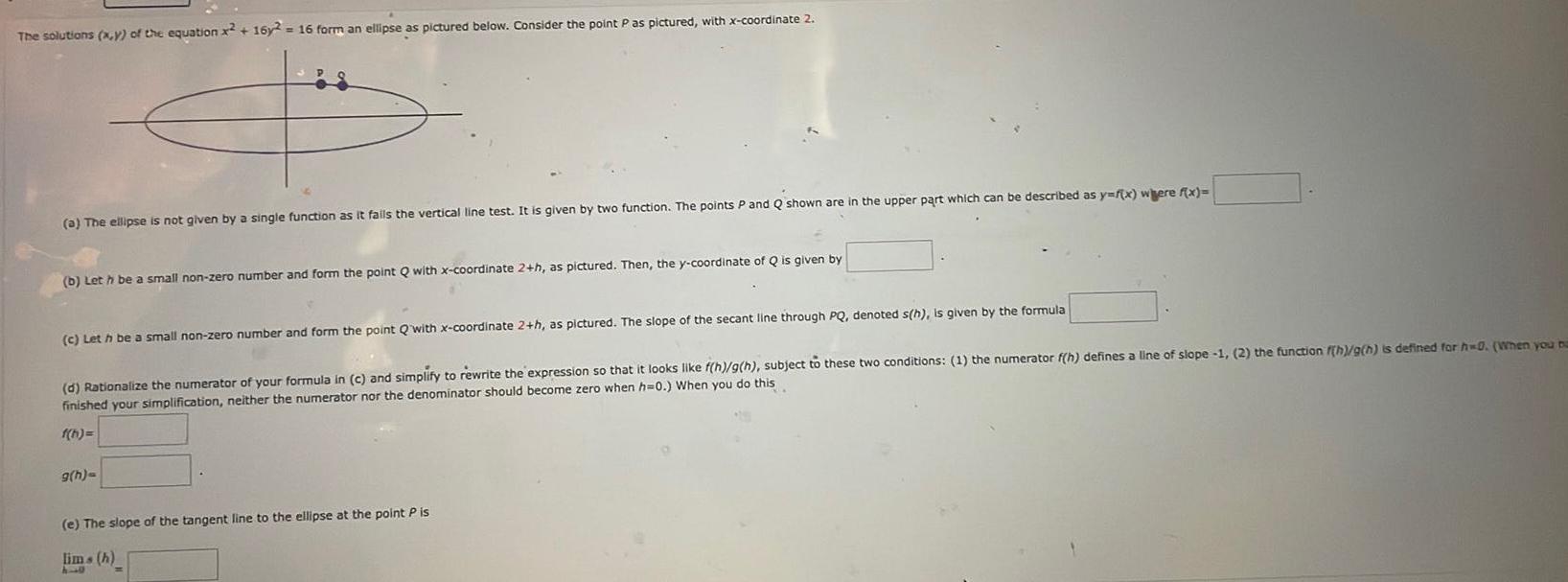
The solutions x y of the equation x2 16y2 16 form an ellipse as pictured below Consider the point P as pictured with x coordinate 2 a The ellipse is not given by a single function as it fails the vertical line test It is given by two function The points P and Q shown are in the upper part which can be described as y f x were f x b Let h be a small non zero number and form the point Q with x coordinate 2 h as pictured Then the y coordinate of Q is given by c Let h be a small non zero number and form the point Qwith x coordinate 2 h as pictured The slope of the secant line through PQ denoted s h is given by the formula d Rationalize the numerator of your formula in c and simplify to rewrite the expression so that it looks like f h g h subject to these two conditions 1 the numerator f h defines a line of slope 1 2 the function f h g h is defined for h 0 When you bu finished your simplification neither the numerator nor the denominator should become zero when h 0 When you do this 1 h g h e The slope of the tangent line to the ellipse at the point P is lims h 110

Kunduz · Accepted Answer

Click to see the answer