Your manufacturing plant produces air bags and it known that

Last updated: 4/17/2023

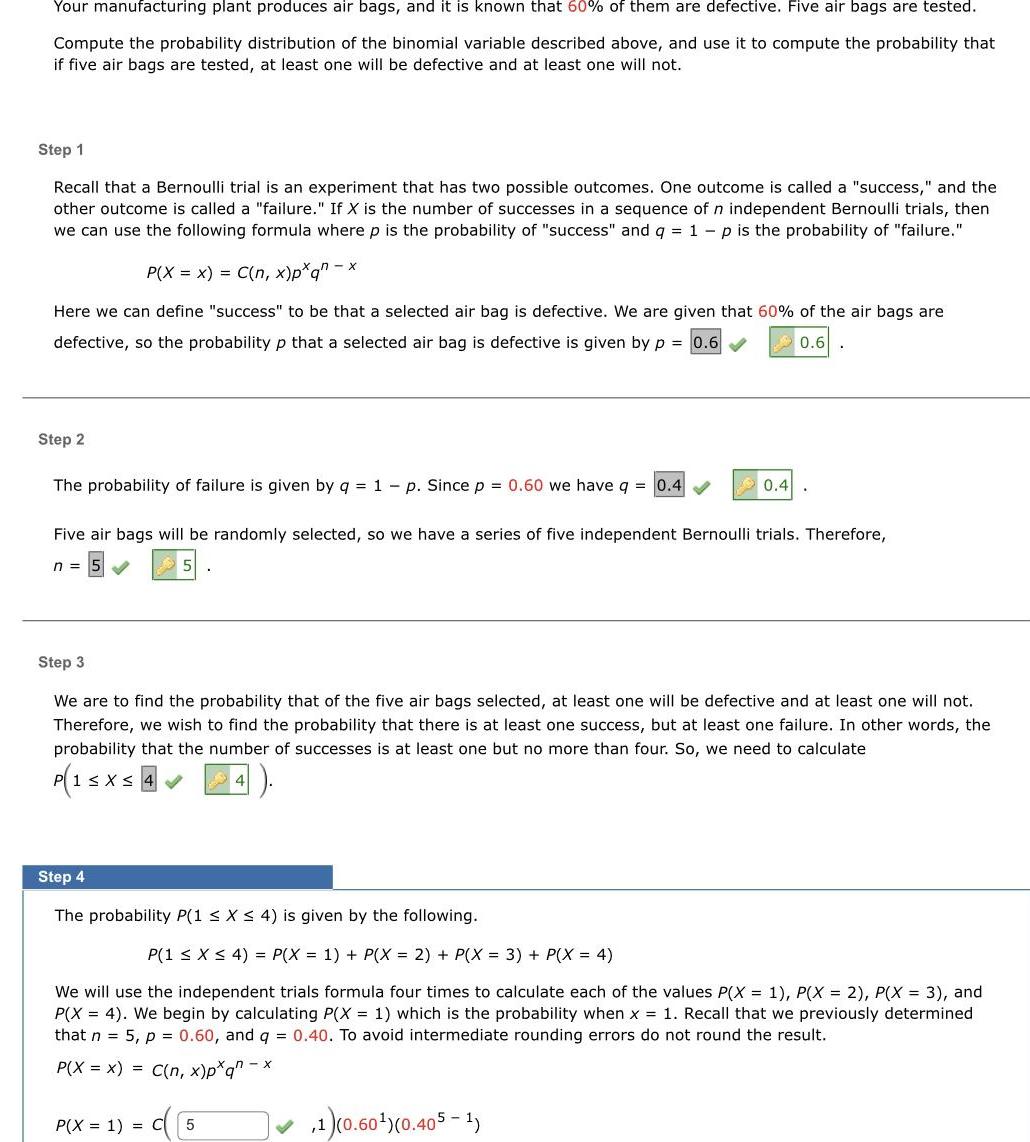
Your manufacturing plant produces air bags and it known that 60 of them are defective Five air bags are tested Compute the probability distribution of the binomial variable described above and use it to compute the probability that if five air bags are tested at least one will be defective and at least one will not Step 1 Recall that a Bernoulli trial is an experiment that has two possible outcomes One outcome is called a success and the other outcome is called a failure If X is the number of successes in a sequence of n independent Bernoulli trials then we can use the following formula where p is the probability of success and q 1 p is the probability of failure P X x C n x p q x Here we can define success to be that a selected air bag is defective We are given that 60 of the air bags are defective so the probability p that a selected air bag is defective is given by p 0 6 0 6 Step 2 The probability of failure is given by q 1 p Since p 0 60 we have q 0 4 n Five air bags will be randomly selected so we have a series of five independent Bernoulli trials Therefore Step 4 The probability P 1 x 4 is given by the following Step 3 We are to find the probability that of the five air bags selected at least one will be defective and at least one will not Therefore we wish to find the probability that there is at least one success but at least one failure In other words the probability that the number of successes is at least one but no more than four So we need to calculate 1 x 4 0 4 P X 1 C P 1 x 4 P X 1 P X 2 P X 3 P X 4 We will use the independent trials formula four times to calculate each of the values P X 1 P X 2 P X 3 and P X 4 We begin by calculating P X 1 which is the probability when x 1 Recall that we previously determined that n 5 p 0 60 and q 0 40 To avoid intermediate rounding errors do not round the result P X x C n x pxq x 5 1 0 60 0 405 1