Sinüs Nedir?
Sinüs, trigonometrinin bir konseptidir ve matematikte kullanılır. Genellikle açı ölçülerini ifade etmek için kullanılan bir fonksiyondur. Sinüs fonksiyonu, bir dik üçgenin bir açısının karşısındaki kenarın hipotenüse olan oranını ifade eder.
Örneğin, dik üçgenin bir açısını θ olarak adlandıralım. Bu açının karşısındaki kenara “karşı kenar” denir, hipotenüse denk gelen kenara ise “hipotenüs” denir. Sinüs fonksiyonu şu şekilde ifade edilir:
sin(θ) = karşı kenar / hipotenüs
Bu formül, bir açının sinüs değerini hesaplamak için kullanılır. Sinüs fonksiyonu genellikle trigonometrik hesaplamalarda, fizik problemlerinde, mühendislik uygulamalarında ve diğer matematiksel alanlarda kullanılır. Sinüs fonksiyonunun değerleri genellikle -1 ile 1 arasında değişir.
Sinüs Teoremi Özellikleri
Sinüs teoremine göre bir üçgende her kenarın uzunluğu ile bu kenarın karşısındaki açının sinüs değeri arasındaki oran üç kenar için de aynıdır.
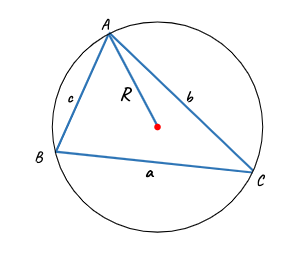
Şekilde verilen üçgende a / sinA = b / sinB = c / sinC = 2R olarak hesaplanır.
Sinüs Teoremi Ne İçin Kullanılır?
Sinüs teoremi genellikle iki açı ve iki kenar verildiğinde üçgenin bilinmeyen kenar uzunluğunu bulmak için ya da çevrel çember ile ilgili bilgiler verildiğinde kullanılır.
Sinüs Alan Formülü
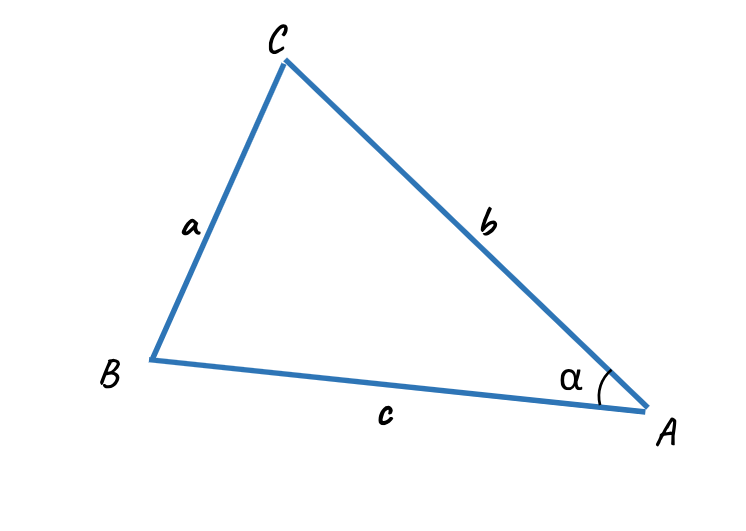
Şekildeki üçgenin alanını belirten sin alan formülü:
A(ABC) = 1/2 * a * b * sinC
A(ABC) = 1/2 * b * c * sinA
A(ABC) = 1/2 * a * c * sinB
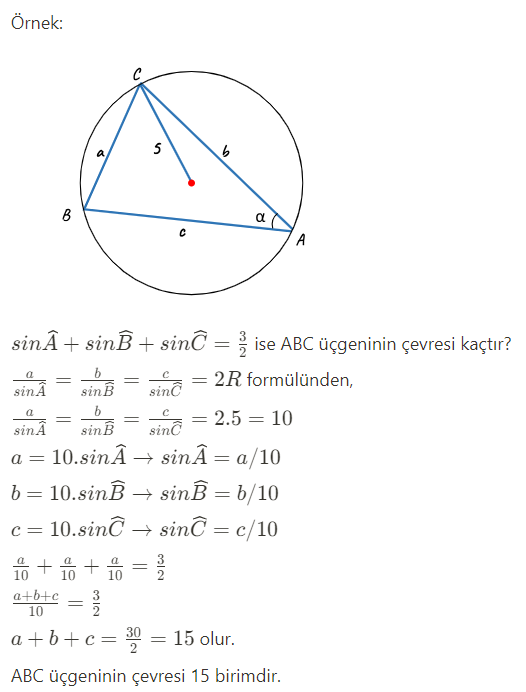
Sinüs Teoremi Soruları Nasıl Çözülür?
Sinüs vs. Kosinüs Arasındaki Farklar
Sinüs ve kosinüs, trigonometrik fonksiyonlar olup birbirlerine benzer özelliklere sahiptirler, ancak bazı temel farklar vardır:
- Tanımlar:
- Sinüs (sin): sin(θ) = karşı kenar / hipotenüs
- Kosinüs (cos): cos(θ) = komşu kenar / hipotenüs
- İfade Edilen Açılar:
- Sinüs, bir açının karşısındaki kenarın hipotenüse olan oranını ifade eder.
- Kosinüs, bir açının bitişik kenarının hipotenüse olan oranını ifade eder.
- Bağıntı:
- sin(θ) = cos(2π−θ)
- Yani, bir açının sinüs değeri, o açının bütünler açısının kosinüs değerine eşittir.
- Değer Aralığı:
- Her iki fonksiyonun değerleri -1 ile 1 arasındadır. Ancak, açılar farklı olduğu sürece, sinüs ve kosinüs değerleri genellikle farklıdır.
- Faz Farkı:
- Sinüs ve kosinüs fonksiyonları arasında 90 derecelik bir faz farkı vardır. Yani, sin(θ)=cos(θ−2π).
- Grafikler:
- Sinüs fonksiyonu, y=sin(x) grafiği, x-eksenine göre 2π radyan kaymış bir kosinüs grafiği ile aynıdır.
Bu farklar, trigonometri alanında bu iki fonksiyonun nasıl kullanıldığını ve birbirleriyle nasıl ilişkilendiğini anlamak için önemlidir. Sinüs ve kosinüs fonksiyonları, birçok fiziksel ve matematiksel bağlamda kullanılır ve birbirlerine olan bu temel ilişki, trigonometrik hesaplamalarda önemli bir rol oynar.
Dik Üçgen Nedir?
Dik üçgen, bir üçgenin bir açısının tam olarak 90 derece olduğu özel bir üçgendir. Bu açı, üçgenin bir köşesinde bulunan dik açıdır. Dik üçgenin karşısındaki kenar, dik açının karşısındaki kenar olarak adlandırılır ve bu kenara hipotenüs denir. Dik üçgenin diğer iki kenarı ise dik açının bitişik olduğu kenarlar olarak adlandırılır.
Birim Çember Nedir?
Birim çember, merkezi orijin (0,0)(0,0) ve yarıçapı 1 olan bir çembere denir. Matematiksel olarak, birim çember şu denklemi karşılar:
x² + y² = 1
Burada x ve y çember üzerindeki bir noktanın koordinatlarıdır. Birim çember genellikle koordinat düzleminde çizilir ve trigonometrik fonksiyonlarla ilgili konseptleri görselleştirmek için kullanılır.
Birim çember, trigonometrik fonksiyonların (sinüs ve kosinüs gibi) grafiklerini anlamak, trigonometrik hesaplamalarda kullanmak için önemlidir. Ayrıca, karmaşık sayılar ve matematiksel analiz gibi konularda da kullanılan temel bir geometrik yapıdır.

