Türev Nedir?
Türevin kelime anlamı Türk Dil Kurumu’na göre “türemiş veya üretilmiş şey” demektir. Matematikteki türev ise “değişken artması sıfıra giderken, fonksiyonun artmasının değişken artmasına oranı limiti” olarak tanımlanır.
Sabit Fonksiyonun Türevi
Sabit fonksiyonların türevi 0’dır. Yani; f(x)=c ve c ϵ R için f'(x) = 0 olur.
Örnek: f(x) = 12 olsun. Bu durumda sabit fonksiyon olduğu için her noktasındaki türevi 0’dır.
f'(x) = 0 yazılır.
Üslü Fonksiyonların Türevi
N ϵ R olmak üzere f(x) = x^n ise f'(x) = n. x^{n-1} yazılır. Yani üslü fonksiyonlarda türev alırken terimin kuvveti, terimin başına katsayı olarak gelir ve terimin kuvveti 1 azaltılır.
Örnek: f(x) = x^4 ise f'(x) = 4. x^{4-1} = 4.x^3 olur.
Eğer fonksiyonumuz katsayılı olarak verilirse de çözmek çok kolay. c ϵ R bir sabit sayı olmak üzere fonksiyon c.f(x) şeklinde verildiğinde fonksiyonun türevi c . f’(x) olur.
Örnek: f(x) = 7.x^3 ise f'(x) = 7.3. x^{3-1} = 21.x^2 olur.
İki Fonksiyonun Toplamının Türevi
İki fonksiyonun toplamının türevi [f(x) + g(x)]’ = f’(x) + g’(x) şeklindedir. f ve g fonksiyonları x noktasında türevli iki fonksiyon olmak üzere, f + g fonksiyonu da x noktasında türevlidir.
İki Fonksiyonun Çarpımının Türevi
f(x) ve g(x), x noktasında türevli iki fonksiyon olmak üzere; çarpım türevi
[f(x) . g(x)]’ = f’(x) . g(x) + f(x) . g’(x) şeklinde yazılır. Ve bu elde ettiğimiz çarpım fonksiyonu da x noktasında türevlidir denir.
Not: “birincinin türevi çarpı ikinci + ikincinin türevi çarpı ikinci” diyerek formülü daha kolay hatırlayabilirsin.

İki Fonksiyonun Bölümünün Türevi
f ve g, x noktasında türevli olan iki fonksiyon ve g(x) ≠ 0 olmak üzere,
f(x) / g(x) fonksiyonunun da bölmenin türevi x noktasında alınabilir. Bu iki fonksiyonun bölüm türevi aşağıdaki formül ile bulunur:
[f'(x).g(x)-f(x).g'(x)] / g²(x)

İki Fonksiyonun Farkının Türevi
İki fonksiyonun farkının türevi [f(x) – g(x)]’ = f’(x) – g’(x) şeklindedir. İki fonksiyonun farkının türevi alınırken verilen fonksiyonların ayrı ayrı türevleri alınır ve çıkarma işlemi uygulanır.
Köklü Fonksiyonların Türevi
Köklü şekilde verilen fonksiyonlarda kökün türevini almanın yolu bu fonksiyonları üslü halde yazmaktır.
Örneğin, kök x in türevi bulunurken ilk olarak köklü sayı üslü halde yazılır.
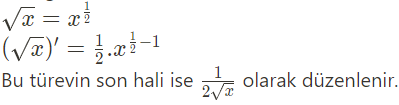
Mutlak Değer Fonksiyonunun Türevi
Mutlak değer fonksiyonunda mutlak değerin içini sıfır yapan değerler fonksiyonun kritik noktalarıdır. Bu kritik noktalarda sağdan ve soldan türev incelenmelidir.
Kritik noktaların dışındaki noktalarda türev alırken mutlak değerin içindeki ifadenin işaretine göre dışarı çıkarıldıktan sonra türev alınır ve türevi sorulan nokta bu aşamadan sonra yerine yazılır.
Bileşke Fonksiyonun Türevi
y = f(x) = (hog)(x) ise, bileşke türev
y’ = f’(x) = h’(g(x)) . g’(x) olur. Burada önemli nokta ‘’için türevi’’ni yani g’(x)’i unutmamaktır.

Zincir Kuralı
y, u değişkenine bağlı
u, v değişkenine bağlı,
v, x değişkenine bağlı türevlenebilen fonksiyonlardır.
y = f(u), u = g(v), v = h(x) olmak üzere;
dy / dx = dy / du * du / dv * dv / dx biçiminde yazılır. Bu kurala zincir kuralı denir.

Ters Fonksiyonun Türevi
Bir f(x) fonksiyonunun tersinin türevi (f^-1)'(y)= 1/f'(x) şeklinde gösterilir.
Logaritmik Fonksiyonların Türevi
f: R → R^+ ve a sayısı 1’den farklı pozitif bir reel sayı olmak üzere,

Üstel Fonksiyonların Türevi
f fonksiyonu a^x formatında bir üstel fonksiyonu olsun. Üstel fonksiyonun türevi f'(x) = a^x * lna şeklinde gösterilir.
Eğer üstel kısımda bir g(x) fonksiyonu varsa; yani f(x) = a^g(x) formatında bir fonksiyonsa f'(x) = a^g(x) * lna * g'(x) olur.
Trigonometrik Fonksiyonların Türevi
Trigonometrik fonksiyonlar türevlerinin tanımlı olduğu aralıklarda,
y = f(x) = sinx ise y’ = cosx
sinx türevi cosx’tir.
y = f(x) = cosx ise y’ = -sinx
cosx türevi eksi sinx’tir.
y = f(x) = tanx ise y’ = sec²x
tan türevi sec karedir.
y = f(x) = cotx ise y’ = -csc²x
cotx türevi eksi csc kare x’tir.
y = f(x) = secx ise y’ = secx . tanx
secx türevi secx çarpı tanx’tir.
y = f(x) = cscx ise y’ = -cscx . cotx
cscx türevi eksi cscx çarpı cotx’tir.
Parçalı Fonksiyonların Türevi
Parçalı fonksiyonlarda türev alırken fonksiyonun kritik noktalarında sağdan ve soldan türevler incelenmelidir.
Parçalı fonksiyon kritik noktalarında sürekli olmalıdır. Aksi halde bu noktalarda türevi yoktur.
Parçalı fonksiyonun kritik noktalarında sağdan ve soldan türev birbirine eşit olmalıdır. Aksi halde bu noktalarda türevi yoktur.

