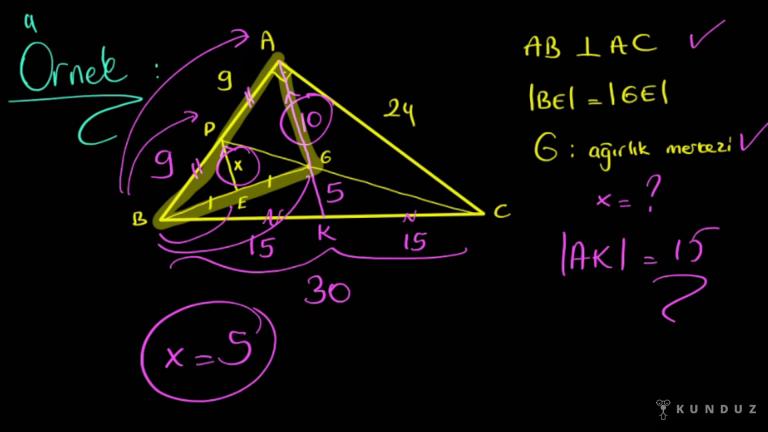
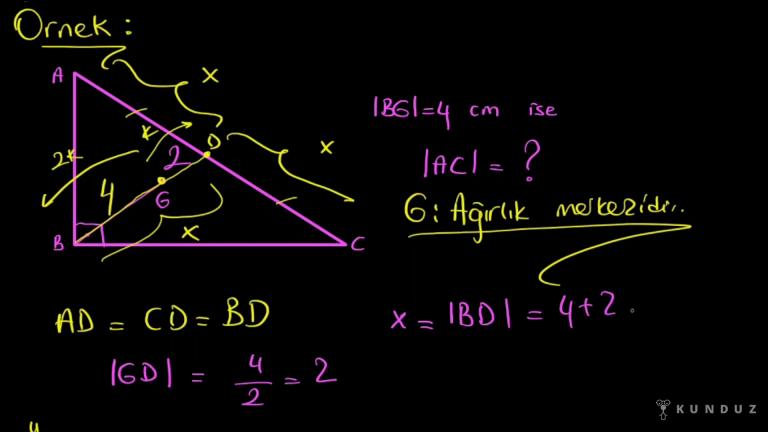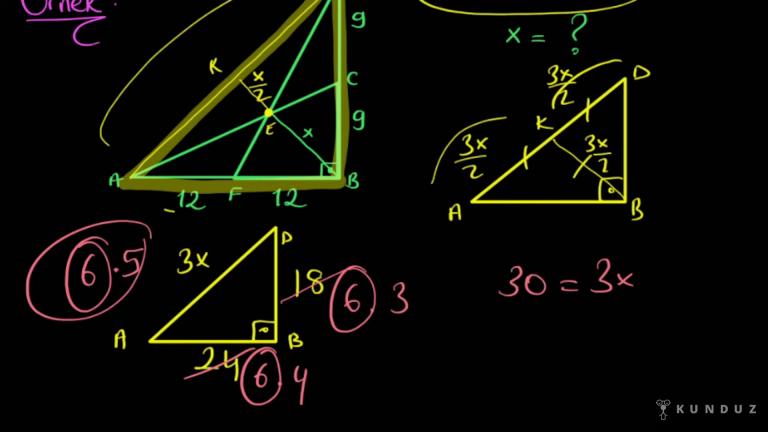Merhabalar, konumuz kenar ortay kenar orta anlamaktan bahsedeceğiz, bunun bazı özel durumlarını, uzunluk hesaplarını anlatacağım.
Bazı yerlerin nasıl bulunduğunu yine dilim döndüğünce sizlere aktarmaya çalışacağım.
Birkaç gösterim üzerinden bunları neden kullandığımız da açıklarım.
Sizlere başlayalım.
Nedir bu kenar ortay?
Adı üstünde kenar.
Ortalam haktan bahsediyoruz.
Özel bir durum olduğu için sizlere aktarıyoruz.
Nasıl açıyı ortak sayıp özel bir durum olan açı ortayı açıklıyor, sag kenarı da ortadan kesen doğru parçalarının özel durumlarını sizlere açıklayacağız.
Tabiki de bir köşeden karşısındaki kenarın ortasına çizilen doğru parçasına kenar ortay diyoruz.
Kenarın herhangi bir yerinden yani buradan şuradan alınan ayÄ yakın olan bir yerden bahsetmiyoruz.
Yani buradan şuranın ortasına çizmekten bahsetmiyoruz.
Köşeden çözeceksiniz.
Yani burada gördüğünüz A'ya ait kenar ortay ve A olarak isimlendiriliyor.
B eden bir çizgi çektiniz.
Yani şöyle bir beden.
Burayı ortalamanın 3 çektiniz.
Bu gördüğünüz ve B olacaktı.
Bu gördüğünüz de edersek yani B dediğime de ve B diyecektik.
C denmiş diyecektiniz ve C edecektiniz yani.
Bunun özel durumu ne?
Neden anlatıyorsun bunu hoca e geleyim.
İlk ve en önemli özel durumumuz ağırlık merkezleri arkadaşlar.
Ağırlık merkezini anlatalım.
Kenar orta ayların kesişim merkezini ağırlık merkezi adını veriyoruz.
Yani siz üç tane kenar ortay çı derseniz ortak bir yerde kesilirler.
Ya da iki tane kenar ortak çizer iseniz ağa'dan ya da beden çizdiniz.
Diğer iki kenar orta in kesişim noktasından üçüncü geçmek zorundadır arkadaşlar.
O yüzden diyoruz üçü bir noktada kesişir.
Üçgenin iç açı ortasında nasıl kesişim merkezini yani iç teğet çemberinin önemli olarak aktardığı isek bu da o önemdedir.
Ağırlık merkezi sadece bu ders dahilinde değil, ayrıca mesela fizik dersinde de kullanımı olan bir konudur.
Detaylıca bilmemiz elzemdir.
Ağırlık merkezi dediğimiz denge merkezidir.
Siz bir üçgen de denge arıyorsanız ağırlık merkezinde o dengeyi bulabilirsiniz.
O üçgenin alanının ya da ağırlığını, merkezini mi arıyorsunuz?
İşte bu noktaya gelirsiniz.
Mesela üçgen şeklinde bir heykel yaptınız.
Bunu öyle düşünün.
Asmak, bir sergilemek istiyorsunuz.
İşte ağırlık merkezini bilmelisiniz ki nasıl dengede dengede duracağını tahmin edebilirsiniz arkadaşlar.
Şimdi ağırlık merkezi de kendi içinde bir özel duruma tabidir.
Nedir bu ağırlık?
Merkezi kenar ortay üzerinde herhangi bir yer de değildir.
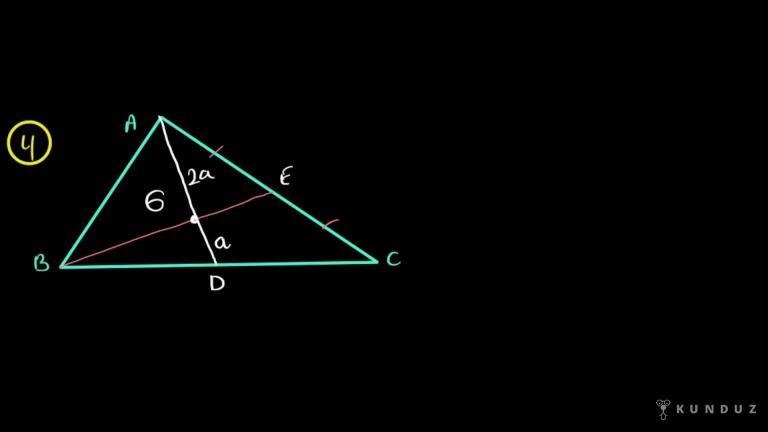
Zaten öyle olsa büyük bir ihtimalle sizi anlatmanızı konu ağırlık merkezi kenar ortayı köşeye uzaklığı iki birim olacak şekilde, kenara uzaklığı da 1 birim olacak şekilde böler.
Ne demek istiyorum?
Ağa'dan bir kenar ortay mi çizdiniz?
İşte ağırlık merkezini arıyoruz.
Konumuz o.
Diyorum ki ağırlık merkezi bu.
Çizdiğiniz bu kenar ayın üzerinde kenara 1 birim olacak şekilde, köşeye de 2 birim olacak şekilde uzaklıktadır.
Ya da aynı şekilde beyden çizdiniz B eden bu kenar ortalanan B değil çizdiniz bu ve beydir veyahut kenar ortağıdır.
İşte diyorum ki burada ağırlık merkezini mi arıyorsunuz?
Yani şunun olmadığını düşünün.
Ağırlık merkezi nerededir diye arıyoruz arkadaşlar.
Fazla sildik.
Diyeceğim ki işte ke köşeye uzaklığı 2 birim yani buradan 2 birim geleceğim.
Buradan bir birim geleceğim ve ağırlık merkezine ulaşacak.
E bunu nasıl yaparım?
Ölçer'in Burayı üçe bölelim buradan o bir bölücü gelirim.
Demek ki burası kesinlikle ağırlık merkezidir derim.
Böyle aklınızda kalabilir.
Yani bunları anlatalım.
Peki hocam ben nasıl bulacağım bu ağırlık merkezini derseniz, işte şimdi sırada anlatacaklarım tam size göre.
Sana üçgen şeklinde mesela küçük bir arsa planı verseler nasıl bulacaksın ağırlık merkezini?
Elinde sadece metre var diyelim.
Hadi bakalım söyleyeyim bir.
Yani bunun anlatım yolları var.
Hepsini anlatacağım.
Teker teker üstünden gidelim.
Bir tane kenar seçiyorsun.
Bunları metreyle ölçüyor.
Sün iki tanesi hiç pardon iki tane kenar seçiyorsunuz ve bunları metreyle ölçüyor.
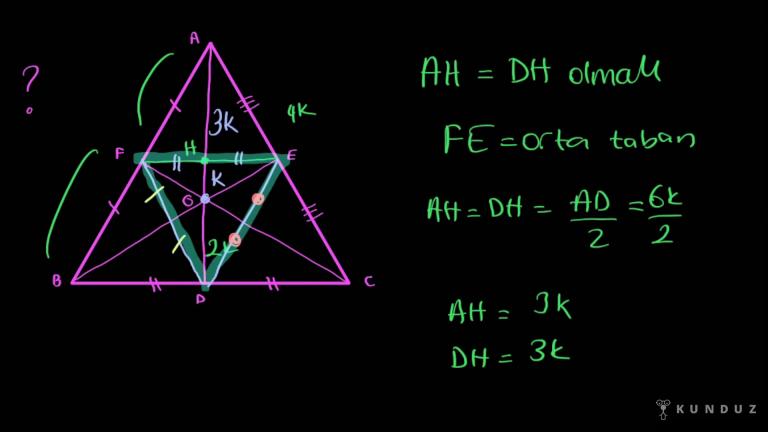
Mesela burada BBC'yi ve Ağca'yı metre ile ölçü Örs'ün sonra bu kenarlarını, orta noktalarını bulup işaret.
Bbc'nin orta noktası bu olsun, A.
C'nin orta noktası burası olsun.
Hedeflerimizde verelim.
Tv 3 sonra bu orta noktaları ve köşeleri birleştir.
O zaman burayla burayı birleştiriyor, tüm burayla burayı birleştiriyor.
İşte diyorum ki bunların kesişecek yer kesinlikle ağırlık merkezidir.
Neden buradan çizdiğim kenar orta yoldur.
Buradan çizdiğim kenar orta yoldur.
Çünkü kenarlarının ortalarını buldum ve köşeli birleştirdim.
Demek ki kenar orta yaptım.
O zaman B ve adÄ kenar ortağıdır.
İşte bunların kesişim noktası ağırlık merkezimiz olur.
Arkadaşlar birinci bulma yolu budur.
Peki başka yollarımız yok mu?
Var tabiki de bir 1 tane kenarını ortasını bulun.
Tamam BBC'nin ortasını aldım köşe ile birleştir yani.
Yine kenar orta ayımızı çizdik tamam.
Şöyle orta aldığımızı da gösterelim.
Kenar orta ölçü ne demek istiyorum?
Hak verdim ademi ölçü diyorum.
Git Metreyle Ağa'dan başla, dereye yolunu al ve öç.
Sonra diyoruz ki işte ağırlık merkezi kenara.
Bu ölçünün üçte biri kenar.
Burası ise buradan üçte bir uzaklıkta.
Bu ölçünün dediğim de toplam Aden'in üçte biri.
Köşeden de üçte ikisi uzakta olan noktadır.
Yani burası da iki kere burasına key edersem taviz tabikide.
İşte aradığım nokta buradadır.
Yani diyeceğim ki bir kenara ortay çiziyorum.
Ondan sonra ölçtüğü kenar ortay uzunluğunun bir bölümünü alıp bir böyle üçüyle kenardan uzak taşıyorum.
Iki bölüm üçüyle de köşeden uzaklaşarak G noktasına geliyorum.
Doğru yani doğru parçası üzerinde kenar orta üzerine gidiyoruz.
Bitti mi?
Bitmedi, devam ediyoruz.
Eğer köşelerden çizilen iki doğru parçası birbirini.
Tabana bir köşeye 2 birim uzaklıkta bölecek şekilde kesişiyor.
Bunların kesişim yeri yine ağırlık merkezidir.
Bakın burada ilk başta bunları kenar orta olduğu söylenmedi.
Tamam, köşelerden çizilen iki doğru parçası birbirini tabana bir köşeye iki birim uzaklıkta.
Hemen yazalım bir tane çizdim.
Bakın kenar ortada olduğunu söylemiyorum.
Diyorum ki ikinciyi de çiziyorum, çizdim.
Dedim ki bu T'yi iki T olarak bölündü.
Diğer parçam K2 KE olarak bölündü.
Bunların kenar ortası olduğuna dair hiçbir bilgim yok.
Sadece birbirleriyle kesildikten sonra aldıkları oranları yazdım.
T'ye 2, tekkeye 2 ke olarak bölünmüş.
O zaman diyeceğim ki burada gördüğünüz G noktası kesinlikle ağırlık merkezi dir.
Arkadaşlar bir bulma yolu da budur.
Üstte anlattığım gibi kenar orta çizmeye gerek yok yani.
Bunlar tabii bu oranı sağladıkları için kenar orta yolluyorlar da kenar ortaya olduklarını ben başta bilmiyordum.
Tamam mı?
Soru bana vermemişti ya da yaşadığım olay bunu bana göstermemişti.
Ama bu iki doğru parçasının birbiriyle yaptığı oranlar işte bana ağırlık merkezi olduğunu ispatlar nitelikte.
O yüzden bunu böyle anlattık arkadaşlar.
Yani buradan sonra artık bu oranı gördükten sonra bunların kenar orta olduğunu biliyorum.
Bunları ben yazabilirim.
Son olarak bunların kenar ortağı olduğunu gördüm ve bunların bu işittiğini yazabilirim.
Son olarak geçelim.
Bir kenara ortay çizdiniz diyelim.
Şuradan Bey'den başlayalım.
Kenar ortayı çizdik tamam.
İkinci adımda diyeceğiz ki kenar ortası çizdik.
Çizgimizi gösterelim diğer çizdiğiniz parça.
Eğer onu yine bir ve iki oranında bire iki oranında kesiyor ise yani ne demek istiyorum?
Ağdan bir tane çizdiniz bakın kenar orta çizdiniz demiyorum adam bir doğru parçası çizdiniz karşı kenara giden tamam diyorum ki işte bu.
Eğer burayı ağaya iki bölüm varsa bu nokta ağırlık merkezidir.
Bakın ilk çizdim kenar ortağıydı.
Tamam onun olduğunu gösterdim ama ikinci çizdiğim yani A de Şüheda E'ye verelim.
Adä kenar ortay olarak belirtilmedi.
Ne dedim 1'e 2 oranında böldü ama B.
Ile beraber birbirlerini.
O zaman diyeceğim ki G noktası yani bunların kesişimi kesinlikle ağırlık merkezidir.
Yani yine bir ağırlık merkezi bulma yolu bu.
Pardon bu denilebilir.
Merkezidir Tamam.
Bazı yerlerin nasıl bulunduğunu yine dilim döndüğünce sizlere aktarmaya çalışacağım.
Birkaç gösterim üzerinden bunları neden kullandığımız da açıklarım.
Sizlere başlayalım.
Nedir bu kenar ortay?
Adı üstünde kenar.
Ortalam haktan bahsediyoruz.
Özel bir durum olduğu için sizlere aktarıyoruz.
Nasıl açıyı ortak sayıp özel bir durum olan açı ortayı açıklıyor, sag kenarı da ortadan kesen doğru parçalarının özel durumlarını sizlere açıklayacağız.
Tabiki de bir köşeden karşısındaki kenarın ortasına çizilen doğru parçasına kenar ortay diyoruz.
Kenarın herhangi bir yerinden yani buradan şuradan alınan ayÄ yakın olan bir yerden bahsetmiyoruz.
Yani buradan şuranın ortasına çizmekten bahsetmiyoruz.
Köşeden çözeceksiniz.
Yani burada gördüğünüz A'ya ait kenar ortay ve A olarak isimlendiriliyor.
B eden bir çizgi çektiniz.
Yani şöyle bir beden.
Burayı ortalamanın 3 çektiniz.
Bu gördüğünüz ve B olacaktı.
Bu gördüğünüz de edersek yani B dediğime de ve B diyecektik.
C denmiş diyecektiniz ve C edecektiniz yani.
Bunun özel durumu ne?
Neden anlatıyorsun bunu hoca e geleyim.
İlk ve en önemli özel durumumuz ağırlık merkezleri arkadaşlar.
Ağırlık merkezini anlatalım.
Kenar orta ayların kesişim merkezini ağırlık merkezi adını veriyoruz.
Yani siz üç tane kenar ortay çı derseniz ortak bir yerde kesilirler.
Ya da iki tane kenar ortak çizer iseniz ağa'dan ya da beden çizdiniz.
Diğer iki kenar orta in kesişim noktasından üçüncü geçmek zorundadır arkadaşlar.
O yüzden diyoruz üçü bir noktada kesişir.
Üçgenin iç açı ortasında nasıl kesişim merkezini yani iç teğet çemberinin önemli olarak aktardığı isek bu da o önemdedir.
Ağırlık merkezi sadece bu ders dahilinde değil, ayrıca mesela fizik dersinde de kullanımı olan bir konudur.
Detaylıca bilmemiz elzemdir.
Ağırlık merkezi dediğimiz denge merkezidir.
Siz bir üçgen de denge arıyorsanız ağırlık merkezinde o dengeyi bulabilirsiniz.
O üçgenin alanının ya da ağırlığını, merkezini mi arıyorsunuz?
İşte bu noktaya gelirsiniz.
Mesela üçgen şeklinde bir heykel yaptınız.
Bunu öyle düşünün.
Asmak, bir sergilemek istiyorsunuz.
İşte ağırlık merkezini bilmelisiniz ki nasıl dengede dengede duracağını tahmin edebilirsiniz arkadaşlar.
Şimdi ağırlık merkezi de kendi içinde bir özel duruma tabidir.
Nedir bu ağırlık?
Merkezi kenar ortay üzerinde herhangi bir yer de değildir.
Zaten öyle olsa büyük bir ihtimalle sizi anlatmanızı konu ağırlık merkezi kenar ortayı köşeye uzaklığı iki birim olacak şekilde, kenara uzaklığı da 1 birim olacak şekilde böler.
Ne demek istiyorum?
Ağa'dan bir kenar ortay mi çizdiniz?
İşte ağırlık merkezini arıyoruz.
Konumuz o.
Diyorum ki ağırlık merkezi bu.
Çizdiğiniz bu kenar ayın üzerinde kenara 1 birim olacak şekilde, köşeye de 2 birim olacak şekilde uzaklıktadır.
Ya da aynı şekilde beyden çizdiniz B eden bu kenar ortalanan B değil çizdiniz bu ve beydir veyahut kenar ortağıdır.
İşte diyorum ki burada ağırlık merkezini mi arıyorsunuz?
Yani şunun olmadığını düşünün.
Ağırlık merkezi nerededir diye arıyoruz arkadaşlar.
Fazla sildik.
Diyeceğim ki işte ke köşeye uzaklığı 2 birim yani buradan 2 birim geleceğim.
Buradan bir birim geleceğim ve ağırlık merkezine ulaşacak.
E bunu nasıl yaparım?
Ölçer'in Burayı üçe bölelim buradan o bir bölücü gelirim.
Demek ki burası kesinlikle ağırlık merkezidir derim.
Böyle aklınızda kalabilir.
Yani bunları anlatalım.
Peki hocam ben nasıl bulacağım bu ağırlık merkezini derseniz, işte şimdi sırada anlatacaklarım tam size göre.
Sana üçgen şeklinde mesela küçük bir arsa planı verseler nasıl bulacaksın ağırlık merkezini?
Elinde sadece metre var diyelim.
Hadi bakalım söyleyeyim bir.
Yani bunun anlatım yolları var.
Hepsini anlatacağım.
Teker teker üstünden gidelim.
Bir tane kenar seçiyorsun.
Bunları metreyle ölçüyor.
Sün iki tanesi hiç pardon iki tane kenar seçiyorsunuz ve bunları metreyle ölçüyor.
Mesela burada BBC'yi ve Ağca'yı metre ile ölçü Örs'ün sonra bu kenarlarını, orta noktalarını bulup işaret.
Bbc'nin orta noktası bu olsun, A.
C'nin orta noktası burası olsun.
Hedeflerimizde verelim.
Tv 3 sonra bu orta noktaları ve köşeleri birleştir.
O zaman burayla burayı birleştiriyor, tüm burayla burayı birleştiriyor.
İşte diyorum ki bunların kesişecek yer kesinlikle ağırlık merkezidir.
Neden buradan çizdiğim kenar orta yoldur.
Buradan çizdiğim kenar orta yoldur.
Çünkü kenarlarının ortalarını buldum ve köşeli birleştirdim.
Demek ki kenar orta yaptım.
O zaman B ve adÄ kenar ortağıdır.
İşte bunların kesişim noktası ağırlık merkezimiz olur.
Arkadaşlar birinci bulma yolu budur.
Peki başka yollarımız yok mu?
Var tabiki de bir 1 tane kenarını ortasını bulun.
Tamam BBC'nin ortasını aldım köşe ile birleştir yani.
Yine kenar orta ayımızı çizdik tamam.
Şöyle orta aldığımızı da gösterelim.
Kenar orta ölçü ne demek istiyorum?
Hak verdim ademi ölçü diyorum.
Git Metreyle Ağa'dan başla, dereye yolunu al ve öç.
Sonra diyoruz ki işte ağırlık merkezi kenara.
Bu ölçünün üçte biri kenar.
Burası ise buradan üçte bir uzaklıkta.
Bu ölçünün dediğim de toplam Aden'in üçte biri.
Köşeden de üçte ikisi uzakta olan noktadır.
Yani burası da iki kere burasına key edersem taviz tabikide.
İşte aradığım nokta buradadır.
Yani diyeceğim ki bir kenara ortay çiziyorum.
Ondan sonra ölçtüğü kenar ortay uzunluğunun bir bölümünü alıp bir böyle üçüyle kenardan uzak taşıyorum.
Iki bölüm üçüyle de köşeden uzaklaşarak G noktasına geliyorum.
Doğru yani doğru parçası üzerinde kenar orta üzerine gidiyoruz.
Bitti mi?
Bitmedi, devam ediyoruz.
Eğer köşelerden çizilen iki doğru parçası birbirini.
Tabana bir köşeye 2 birim uzaklıkta bölecek şekilde kesişiyor.
Bunların kesişim yeri yine ağırlık merkezidir.
Bakın burada ilk başta bunları kenar orta olduğu söylenmedi.
Tamam, köşelerden çizilen iki doğru parçası birbirini tabana bir köşeye iki birim uzaklıkta.
Hemen yazalım bir tane çizdim.
Bakın kenar ortada olduğunu söylemiyorum.
Diyorum ki ikinciyi de çiziyorum, çizdim.
Dedim ki bu T'yi iki T olarak bölündü.
Diğer parçam K2 KE olarak bölündü.
Bunların kenar ortası olduğuna dair hiçbir bilgim yok.
Sadece birbirleriyle kesildikten sonra aldıkları oranları yazdım.
T'ye 2, tekkeye 2 ke olarak bölünmüş.
O zaman diyeceğim ki burada gördüğünüz G noktası kesinlikle ağırlık merkezi dir.
Arkadaşlar bir bulma yolu da budur.
Üstte anlattığım gibi kenar orta çizmeye gerek yok yani.
Bunlar tabii bu oranı sağladıkları için kenar orta yolluyorlar da kenar ortaya olduklarını ben başta bilmiyordum.
Tamam mı?
Soru bana vermemişti ya da yaşadığım olay bunu bana göstermemişti.
Ama bu iki doğru parçasının birbiriyle yaptığı oranlar işte bana ağırlık merkezi olduğunu ispatlar nitelikte.
O yüzden bunu böyle anlattık arkadaşlar.
Yani buradan sonra artık bu oranı gördükten sonra bunların kenar orta olduğunu biliyorum.
Bunları ben yazabilirim.
Son olarak bunların kenar ortağı olduğunu gördüm ve bunların bu işittiğini yazabilirim.
Son olarak geçelim.
Bir kenara ortay çizdiniz diyelim.
Şuradan Bey'den başlayalım.
Kenar ortayı çizdik tamam.
İkinci adımda diyeceğiz ki kenar ortası çizdik.
Çizgimizi gösterelim diğer çizdiğiniz parça.
Eğer onu yine bir ve iki oranında bire iki oranında kesiyor ise yani ne demek istiyorum?
Ağdan bir tane çizdiniz bakın kenar orta çizdiniz demiyorum adam bir doğru parçası çizdiniz karşı kenara giden tamam diyorum ki işte bu.
Eğer burayı ağaya iki bölüm varsa bu nokta ağırlık merkezidir.
Bakın ilk çizdim kenar ortağıydı.
Tamam onun olduğunu gösterdim ama ikinci çizdiğim yani A de Şüheda E'ye verelim.
Adä kenar ortay olarak belirtilmedi.
Ne dedim 1'e 2 oranında böldü ama B.
Ile beraber birbirlerini.
O zaman diyeceğim ki G noktası yani bunların kesişimi kesinlikle ağırlık merkezidir.
Yani yine bir ağırlık merkezi bulma yolu bu.
Pardon bu denilebilir.
Merkezidir Tamam.
Sıkça Sorulan Sorular
Kenarortay nedir?
Bir üçgende bir köşeyi karşısındaki kenarın orta noktasına birleştiren doğru parçasına o kenara ait kenarortay denir.
AD = VA : A köşesinden çıkan kenarortay
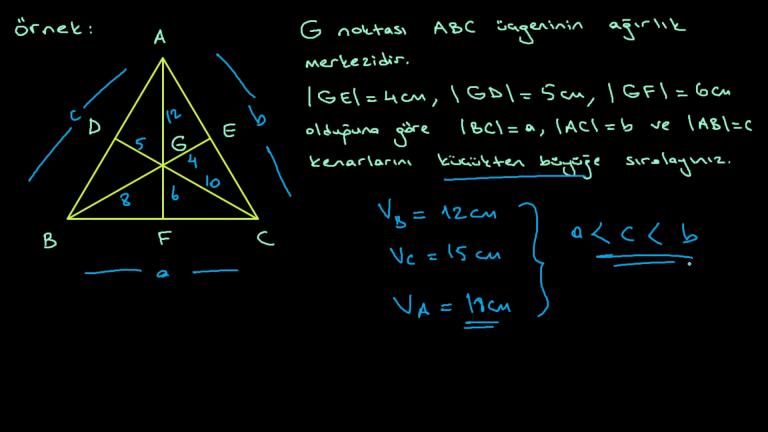
Ağırlık merkezi nedir?
Bir üçgenin kenarortayları bir noktada kesişir. Bu nokta üçgenin ağırlık merkezidir. G noktası, ABC üçgeninin ağırlık merkezi olur.
AD : A köşesine ait kenarortay
FC : C köşesine ait kenarortay
BE : B köşesine ait kenarortay
Ağırlık merkezi kenarortayları köşeye uzaklığı 2 birim, kenara uzaklığı 1 birim olacak şekilde böler.
|AG| = 2.|GD|
|CG| = 2.|GF|
|BD| = 2.|GE| olur.