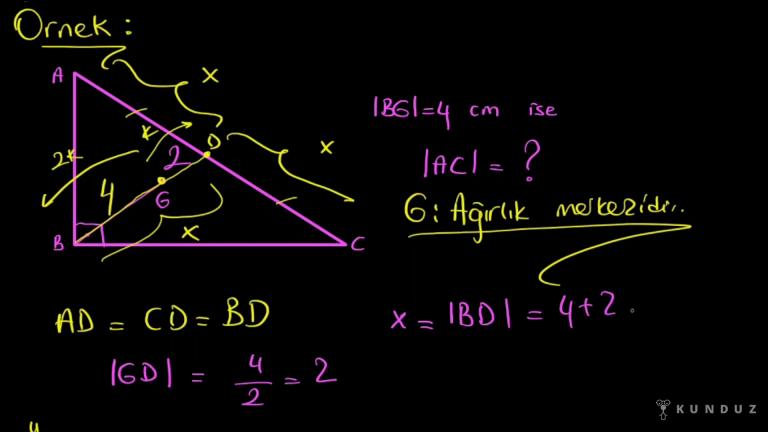Merhabalar, kenarortay konusunda son olarak orta tabanı açıklamak istiyorum.
Siz bir üçgende iki kenarın orta noktasını birleştirirseniz orta taban elde edersiniz.
Gördünüz gibi AB'nin orta noktası D AC'nin orta noktası E, bunların birleşimi orta tabandır.
Bu orta tabanın belirli özellikleri vardır.
Bir, orta taban kesişmediği bu diğer kenara paraleldir.
Yani DE paraleldir BC yazarız.
İki, orta taban yine kesişmediği diğer kenarının uzunluğunun yarısı kadardır.
Yani siz BC'ye 2k derseniz orta taban uzunluğu onun yarısı olur.
Yine anlattık anlattık da bunların hepsi benzerliğe dayanıyor.
Neden benzerliğe dayanıyor açıklayalım.
Üçgenimi çizdim büyük üçgenim ABC'yi çizdim, içinde bir yer aldım, dedim ki bunun orta noktası, bunun orta noktası bu; birleştirdim.
Niye orta taban niye bunlar paralel niye bunların arasında bir iki oran var, diyor.
Şimdi burada A açım alfa olsun, bunları yazdım.
a'yı a bölsün, b'yi b bölsün; bunları da yazdık.
ADE üçgeni ve ABC üçgenine ayrı ayrı bakıyorum a kenarı b kenarı alfa.
2a kenarı iki 2b kenarı alfa, yazdım.
İki üç kere bakıyorum şimdi benzerlik var mı?
A köşesinin açıları aynı mı; alfa alfa, aynı.
Peki iki üçgende karşılıklı kenarlar oranı birbirine eşit mi?
Bakıyorum a bölü b bakıyorum 2a bölü 2b, burada da a bölü b. Demek ki bu oran aynı ve aralarındaki açı eşitse kesinlikle bunlar benzerdir diyoruz.
İşte bu benzerlikten dolayı gelişen kuralları anlatıyoruz size arkadaşlar.
Şimdi paralelliği halen göstermedik.
Madem oran var aralarında nasıl bir oran var; karşılıklı kenarların uzunlukları oranı a bölü 2a, b bölü 2b.
Gördüğünüz gibi a bölü 2a sadeleşir b bölü 2b sadeleşir, 1/2 oran var. Yani diyorum ki bu bunun iki katıdır resmen.
Onu demeye çalışıyorum resmen bu oran bana.
Yani ben buraya C dersem burası bana 2c olmalı 1'e 2 oranı sağlamalıyım çünkü diğerlerinde de o oran var. c'ye 2c olmalı yani siz buraya c dersiniz buraya zaten.
Orta taban kesişmediği diğer kenarın yarısı kadardır, dedim bitti.
Şimdi paralellik neden geldi?
Açılardan gelecek o da.
Bir, burada a'yı gören açma beta desem burada da karşılıklı olarak kenarı gören açıya geçmem lazım.
a'nın karşılıklı olarak buradaki eşiti nedir 2a, demek ki buraya gelip beta yazacağım.
Aynı şekilde B'yi gören teta olsun gel buraya teta'yı yaz.
Hangi açı karşılıklı olarak 2b olmalı o zaman onun karşısında b köşesi var oraya yazdım.
Açıları şimdi büyük üçgene bir döşeyelim b burası beta burası teta ve beta.
Şimdi bu durumun gerçekleşebilmesi için bana ne gerekli arkadaşlar, paralellik gerekli. Paralellikte gördüğünüz gibi yöndeş açılar paralel doğrularda yöndeş açılardan dolayı bu paralelliği de böyle.
Benzerlikten dolayı yine gelişmiş bir kural, tamamı ile bunun üzerinde gerçekleştirilmiş bir kural anlattık arkadaşlar. Şimdi özel olarak yine bir kuraldan bahsedelim.
DE orta taban ise yine ABC'yi çizdim, D noktası orta nokta, E noktası orta nokta bunları birleştirdim DE orta tabandır, tamam.
Tavanın karşısındaki köşeden yani A'dan buradan çıkan doğru parçaları eşit bölünür.
Orta taban tarafından öyle dersen daha iyi olur.
Burada gördüğünüz AN'yi çizdiğiniz anda DE bunu ortadan keser.
Neden?
Çünkü bu oran şu orana eşit olmalı.
Neden?
Çünkü benzerlik var, çünkü paralellik var.
Burada paralellik anlattık demek ki bundan dolayı buradaki oran şuradaki orana eşit olmalı.
Bundan dolayı aynı şekilde yani yerinizi değiştirebilirsiniz.
İsterseniz AP yapın AL eşittir PL olmalı çünkü DE orta taban.
Buradaki oran içeride de sağlanmalı.
Burada sadece bunları göstermek açısından bunları da buraya eklemek istedim.
Burada orta tabanı da dahil olduğu bir kuralı daha aktaracağım sizlere arkadaşlar.
312 kural olarak da aktarılabiliyor bazen arkadaşlar. Gördüğünüz gibi burada 312 kuralı dediğim şey arkadaşlar şurada k'lerin başındaki kat sayılardan geliyor.
Yani burada 312 dememin sebebi 3 burada, bir k burada, 2k burada.
Yani burada, aslında böyle bir durumda şurada gördüğünüz uzunlukların alacakları kat sayı oranlarından bahsediyoruz. Nedir bu?
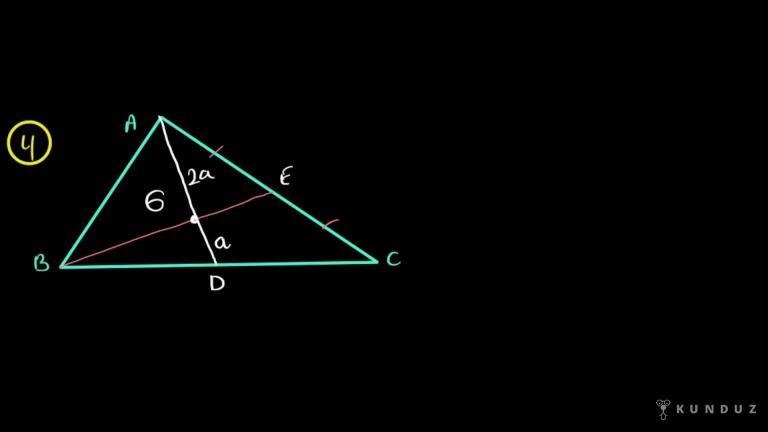
Şunu açıklamak istiyorum: Burada kuralın nasıl geldiğini açıklamak istiyorum. Gelelim buraya; bir üçgen alıyorum, kenarortayları çiziyorum, G noktası yani kesişim yeri ağırlık merkezim oluyor.
Daha sonra ben GD'ye 2k desem, biliyorum ki G ağırlık merkezi olduğu için köşeye iki birim uzaklıkta olacak burası 4k olacak.
Yani AG dediğim 4k, GD dediğim 2k.
2k dememin sebebi tamamen rakamsal olarak rahat hareket edebilmek, yani bir sebebi yok.
Daha sonra diyelim ki bu FB'yi birleştirmek istiyorum.
Şimdi ben FB'yi birleştirirsem neyi yapmış olurum, neyi çizmiş olurum?
Orta tabanı çizmiş olurum.
Şimdi orta tabanı çizersem ne olacak üstte anlattığım kural gibi.
Buradaki oran 1/1 mi, o zaman buradaki oran da 1/1 olmalı neyin eşitliğini yazdım?
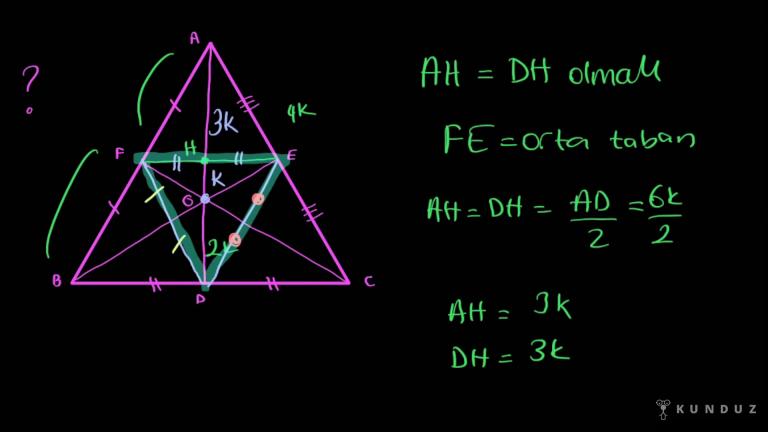
Şurada göstereyim, şu noktaya harf verelim H noktası olsun.
AH eşittir DH olmalı.
Neden olmalı?
Çünkü FE orta tabandır. Orta taban gördüğünüz gibi bu içeride çizdiğim AD'yi ortadan kesmeli.
Yani AH eşittir HD olmalı. Peki bunların ikisinin toplam uzunluğu neydi arkadaşlar?
Şu 4k'yi şöyle göstereyim bari, neyin eşitliği peki, AD'nin yarısı.
Ben AD'yi biliyorum 2K 4K daha 6k idi, 6k bölü 2 .Yani AH'ye de 3k yazacağım, DH'ye de 3k yazacağım, bu kadar.
Şimdi bunları yazarsam peki neler kalıyor elimde?
Geçiyorum DH'ye 3k yazıyorum, DH dedim şu mesafe.
2k burası ise kaldı buraya k.
AH'ye 3k yazıyorum.
Burası zaten onu gösteriyor 3k.
İşte üçgende kenarortay ya da ağırlık merkezi ile bir işlem yaptıysanız arkadaşlar bu şekli aklınızda tutmanız da fayda var.
Bunun içerisinde orta tabanın dahil olduğunu unutmayınız arkadaşlar. Orta tabanın dahilliği çok önemli.
Orta tabanı çizdikten sonra ağırlık merkezi, köşe ve kenar ortay diğer kenara değildi noktalar arasındaki orandan bahsediyoruz.
312 kuralı bunu anlatıyor arkadaşlar.
Burada ufak bir ekleme daha yapalım; bütün kenarların orta noktalarını birleştirirsem, bakın F D E bunlar orta noktalardı birleştirdim diyorum.
Sonra diyorum ki şu üçgene bakınız, FDE'den kastım, diyorum ki bu işte bakınız.
Bu üçgenin ağırlık merkezi büyük üçgenin ağırlık merkezi ile de aynıdır.
Ama neden aynıdır?
Burası buraya eşit değil midir, evet eşit.
Burası buraya eşit değil midir, evet eşit.
Şu nokta şu parça şu parçaya eşit değil midir, evet eşittir. Şimdi bu eşitlikten dolayı çünkü aslında burada çizdiğim FDE de orta tabandır.
O yüzden buradaki oran şuraya da yansır.
Aynı şekilde isterseniz burayı zaten yaptık, isterseniz böyle bakınız buradaki eşitlikler oradan gelmektedir yine. Şimdi FDE üçgenine baktığım anda diyeceğim ki: Ya bu da kenarortay, şu da kenarortay, Bu DH de kenarortay.
Üç tane kenarortaysa demek ki bunların kesişim yeri kesinlikle küçük üçgende de yine G, büyükte zaten G idi küçükte de G olduğunu göstermek istiyorum. Yani bunu göstermek istememin tek sebebi orta noktaları birleştirdiğim anda bu orta noktalarını birleştirdim üçgenin ağırlık merkezi büyük üçgenin de ağırlık merkezi ile aynıdır.
Siz bir üçgende iki kenarın orta noktasını birleştirirseniz orta taban elde edersiniz.
Gördünüz gibi AB'nin orta noktası D AC'nin orta noktası E, bunların birleşimi orta tabandır.
Bu orta tabanın belirli özellikleri vardır.
Bir, orta taban kesişmediği bu diğer kenara paraleldir.
Yani DE paraleldir BC yazarız.
İki, orta taban yine kesişmediği diğer kenarının uzunluğunun yarısı kadardır.
Yani siz BC'ye 2k derseniz orta taban uzunluğu onun yarısı olur.
Yine anlattık anlattık da bunların hepsi benzerliğe dayanıyor.
Neden benzerliğe dayanıyor açıklayalım.
Üçgenimi çizdim büyük üçgenim ABC'yi çizdim, içinde bir yer aldım, dedim ki bunun orta noktası, bunun orta noktası bu; birleştirdim.
Niye orta taban niye bunlar paralel niye bunların arasında bir iki oran var, diyor.
Şimdi burada A açım alfa olsun, bunları yazdım.
a'yı a bölsün, b'yi b bölsün; bunları da yazdık.
ADE üçgeni ve ABC üçgenine ayrı ayrı bakıyorum a kenarı b kenarı alfa.
2a kenarı iki 2b kenarı alfa, yazdım.
İki üç kere bakıyorum şimdi benzerlik var mı?
A köşesinin açıları aynı mı; alfa alfa, aynı.
Peki iki üçgende karşılıklı kenarlar oranı birbirine eşit mi?
Bakıyorum a bölü b bakıyorum 2a bölü 2b, burada da a bölü b. Demek ki bu oran aynı ve aralarındaki açı eşitse kesinlikle bunlar benzerdir diyoruz.
İşte bu benzerlikten dolayı gelişen kuralları anlatıyoruz size arkadaşlar.
Şimdi paralelliği halen göstermedik.
Madem oran var aralarında nasıl bir oran var; karşılıklı kenarların uzunlukları oranı a bölü 2a, b bölü 2b.
Gördüğünüz gibi a bölü 2a sadeleşir b bölü 2b sadeleşir, 1/2 oran var. Yani diyorum ki bu bunun iki katıdır resmen.
Onu demeye çalışıyorum resmen bu oran bana.
Yani ben buraya C dersem burası bana 2c olmalı 1'e 2 oranı sağlamalıyım çünkü diğerlerinde de o oran var. c'ye 2c olmalı yani siz buraya c dersiniz buraya zaten.
Orta taban kesişmediği diğer kenarın yarısı kadardır, dedim bitti.
Şimdi paralellik neden geldi?
Açılardan gelecek o da.
Bir, burada a'yı gören açma beta desem burada da karşılıklı olarak kenarı gören açıya geçmem lazım.
a'nın karşılıklı olarak buradaki eşiti nedir 2a, demek ki buraya gelip beta yazacağım.
Aynı şekilde B'yi gören teta olsun gel buraya teta'yı yaz.
Hangi açı karşılıklı olarak 2b olmalı o zaman onun karşısında b köşesi var oraya yazdım.
Açıları şimdi büyük üçgene bir döşeyelim b burası beta burası teta ve beta.
Şimdi bu durumun gerçekleşebilmesi için bana ne gerekli arkadaşlar, paralellik gerekli. Paralellikte gördüğünüz gibi yöndeş açılar paralel doğrularda yöndeş açılardan dolayı bu paralelliği de böyle.
Benzerlikten dolayı yine gelişmiş bir kural, tamamı ile bunun üzerinde gerçekleştirilmiş bir kural anlattık arkadaşlar. Şimdi özel olarak yine bir kuraldan bahsedelim.
DE orta taban ise yine ABC'yi çizdim, D noktası orta nokta, E noktası orta nokta bunları birleştirdim DE orta tabandır, tamam.
Tavanın karşısındaki köşeden yani A'dan buradan çıkan doğru parçaları eşit bölünür.
Orta taban tarafından öyle dersen daha iyi olur.
Burada gördüğünüz AN'yi çizdiğiniz anda DE bunu ortadan keser.
Neden?
Çünkü bu oran şu orana eşit olmalı.
Neden?
Çünkü benzerlik var, çünkü paralellik var.
Burada paralellik anlattık demek ki bundan dolayı buradaki oran şuradaki orana eşit olmalı.
Bundan dolayı aynı şekilde yani yerinizi değiştirebilirsiniz.
İsterseniz AP yapın AL eşittir PL olmalı çünkü DE orta taban.
Buradaki oran içeride de sağlanmalı.
Burada sadece bunları göstermek açısından bunları da buraya eklemek istedim.
Burada orta tabanı da dahil olduğu bir kuralı daha aktaracağım sizlere arkadaşlar.
312 kural olarak da aktarılabiliyor bazen arkadaşlar. Gördüğünüz gibi burada 312 kuralı dediğim şey arkadaşlar şurada k'lerin başındaki kat sayılardan geliyor.
Yani burada 312 dememin sebebi 3 burada, bir k burada, 2k burada.
Yani burada, aslında böyle bir durumda şurada gördüğünüz uzunlukların alacakları kat sayı oranlarından bahsediyoruz. Nedir bu?
Şunu açıklamak istiyorum: Burada kuralın nasıl geldiğini açıklamak istiyorum. Gelelim buraya; bir üçgen alıyorum, kenarortayları çiziyorum, G noktası yani kesişim yeri ağırlık merkezim oluyor.
Daha sonra ben GD'ye 2k desem, biliyorum ki G ağırlık merkezi olduğu için köşeye iki birim uzaklıkta olacak burası 4k olacak.
Yani AG dediğim 4k, GD dediğim 2k.
2k dememin sebebi tamamen rakamsal olarak rahat hareket edebilmek, yani bir sebebi yok.
Daha sonra diyelim ki bu FB'yi birleştirmek istiyorum.
Şimdi ben FB'yi birleştirirsem neyi yapmış olurum, neyi çizmiş olurum?
Orta tabanı çizmiş olurum.
Şimdi orta tabanı çizersem ne olacak üstte anlattığım kural gibi.
Buradaki oran 1/1 mi, o zaman buradaki oran da 1/1 olmalı neyin eşitliğini yazdım?
Şurada göstereyim, şu noktaya harf verelim H noktası olsun.
AH eşittir DH olmalı.
Neden olmalı?
Çünkü FE orta tabandır. Orta taban gördüğünüz gibi bu içeride çizdiğim AD'yi ortadan kesmeli.
Yani AH eşittir HD olmalı. Peki bunların ikisinin toplam uzunluğu neydi arkadaşlar?
Şu 4k'yi şöyle göstereyim bari, neyin eşitliği peki, AD'nin yarısı.
Ben AD'yi biliyorum 2K 4K daha 6k idi, 6k bölü 2 .Yani AH'ye de 3k yazacağım, DH'ye de 3k yazacağım, bu kadar.
Şimdi bunları yazarsam peki neler kalıyor elimde?
Geçiyorum DH'ye 3k yazıyorum, DH dedim şu mesafe.
2k burası ise kaldı buraya k.
AH'ye 3k yazıyorum.
Burası zaten onu gösteriyor 3k.
İşte üçgende kenarortay ya da ağırlık merkezi ile bir işlem yaptıysanız arkadaşlar bu şekli aklınızda tutmanız da fayda var.
Bunun içerisinde orta tabanın dahil olduğunu unutmayınız arkadaşlar. Orta tabanın dahilliği çok önemli.
Orta tabanı çizdikten sonra ağırlık merkezi, köşe ve kenar ortay diğer kenara değildi noktalar arasındaki orandan bahsediyoruz.
312 kuralı bunu anlatıyor arkadaşlar.
Burada ufak bir ekleme daha yapalım; bütün kenarların orta noktalarını birleştirirsem, bakın F D E bunlar orta noktalardı birleştirdim diyorum.
Sonra diyorum ki şu üçgene bakınız, FDE'den kastım, diyorum ki bu işte bakınız.
Bu üçgenin ağırlık merkezi büyük üçgenin ağırlık merkezi ile de aynıdır.
Ama neden aynıdır?
Burası buraya eşit değil midir, evet eşit.
Burası buraya eşit değil midir, evet eşit.
Şu nokta şu parça şu parçaya eşit değil midir, evet eşittir. Şimdi bu eşitlikten dolayı çünkü aslında burada çizdiğim FDE de orta tabandır.
O yüzden buradaki oran şuraya da yansır.
Aynı şekilde isterseniz burayı zaten yaptık, isterseniz böyle bakınız buradaki eşitlikler oradan gelmektedir yine. Şimdi FDE üçgenine baktığım anda diyeceğim ki: Ya bu da kenarortay, şu da kenarortay, Bu DH de kenarortay.
Üç tane kenarortaysa demek ki bunların kesişim yeri kesinlikle küçük üçgende de yine G, büyükte zaten G idi küçükte de G olduğunu göstermek istiyorum. Yani bunu göstermek istememin tek sebebi orta noktaları birleştirdiğim anda bu orta noktalarını birleştirdim üçgenin ağırlık merkezi büyük üçgenin de ağırlık merkezi ile aynıdır.
Sıkça Sorulan Sorular
Orta taban nedir?
Üçgende herhangi iki kenarın orta noktalarını birleştiren doğru parçasına orta taban denir.
Orta taban ve orta noktası alınmayan diğer kenar birbirine paraleldir ve orta tabanın uzunluğu benzerlikten dolayı kenarın yarısı kadar olur.
D noktası AB kenarının orta noktası
E noktası AC kenarının orta noktası ise;
DE // BC
|BC| = 2.|DE|