TYT‘nin, LGS’nin yani çoğu sınavın önemli konularından EBOB EKOK konusu için temel kuralları ve yöntemleri öğrendikten sonra bolca pratik yapman gerekiyor? Aynı zamanda diğer Matematik konularının içinde de geçebildiği için bu konuyu iyice kavramanı tavsiye ediyoruz. Soru çözmeye başladıktan sonra bu konunun sana çok kolay geleceğine eminiz! Kunduz ekibinden Nurseli, EBOB EKOK konu anlatımı yazısı ile karşında!
EBOB-EKOK konusunun 2019-2020 lise müfredatında yer alan kazanımları şu şekildedir:
Tam sayılarda EBOB ve EKOK ile ilgili uygulamalar yapar.
- Gerçek hayat problemlerine yer verilir.
- Elektronik tablolarda bulunan EBOB ve EKOK fonksiyonlarından yararlanılır.
EBOB EKOK Nedir?
EBOB, En Büyük Ortak Bölen kavramının ve EKOK ise En Küçük Ortak Kat kavramının kısaltması olarak karşımıza çıkıyor. a ve b sayısının en büyük ortak böleni kısaca EBOB(a,b) ve en küçük ortak katı EKOK(a,b) şeklinde gösterilir.
EBOB Özellikleri
a, b, c tamsayıları için c hem a’yı hem b’yi bölüyorsa c’ye a ile b’nin bir ortak böleni denebilir. Hem a’yı hem b’yi kalansız bölen birçok sayı bulabiliriz, bölme işlemi özelliklerini incelemek istersen Bölme Bölünebilme yazımızı inceleyebilirsin!
İşte seçtiğimiz bu iki sayıyı kalansız bölen sayıların en büyüğüne EBOB(a, b) denir.
- c herhangi bir tamsayı olmak üzere; EBOB(c⋅a, c⋅b) = c⋅EBOB(a, b)’dir.
- EBOB(a/d, b/d) = 1 ise d = EBOB(a, b) olur.
- EBOB(a, b) = 1 ise a ve b’ye aralarında asal veya birbirine asal sayılar denir.
- EBOB(a, b) = EBOB(a, c) ise
- EBOB(a2,b2) = EBOB(a2,c2) ve
- EBOB(a, b) = EBOB(a, b, c) olur.
- EBOB(a, b, c) = EBOB(EBOB(a, b), EBOB(a, c))
- EBOB(a, b) = 1 ise EBOB(a2, ab, b2) = 1 olur.
- EBOB(a, b) = EBOB(–a, b) = EBOB(a, –b) = EBOB(–a, –b)
EKOK Özellikleri
- a ve b sıfırdan farklı tamsayılar olsun. a ve b’nin en küçük pozitif ortak katına a ve b’nin en küçük ortak katı denir ve a ve b nin bir katı k ise EKOK(a, b) daima k’yı böler.
- a ve b pozitif tamsayılar olmak üzere; EBOB(a, b)⋅EKOK(a, b) = a⋅b’dir.
Önemli Formüller
En büyük ortak bölen ve en küçük ortak kat konusu altında birçok soru tipi karşına çıkabilir. Sana bu farklı soru tiplerinde EBOB hesaplama ve EKOK hesaplama yaparken yararlı olacağına inandığım birkaç formül vereceğim.
- Eni ve boyu bilinen dikdörtgenleri bir araya getirerek bir kare oluşturman istenebilir. Kenarları a ve b olan dikdörtgenlerden bir kare oluşturabilmek için en az gerekli olan dikdörtgen sayısı aşağıdaki formülle bulunur. En az dikdörtgen derken göreceği gibi EKOK kullandık, fark ettin mi?
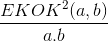
- Küp oluşturmak için ise formülümüz biraz farklı. Farklı ayrıtları a, b ve c olan dikdörtgen prizmaları bir araya getirerek bir küp oluşturmamız istenirse en az gerekli olan prizma sayısı aşağıdaki gibidir:
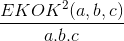
- “Şekilde ebatları verilen dikdörtgen tarlaya eşit aralıklarla ağaç dikilecektir.” cümlesiyle başlayan sorular hepimize tanıdık gelmiştir. İşte bu sorularda kilit formül şöyle: Eşit aralıklı olmak ve köşelere de gelmek koşuluyla gereken en az ağaç sayısı ise aşağıdaki gibi olur:

☀️☀️☀️
Diğer tüm TYT Matematik konuları gibi, EBOB EKOK konusunu tam olarak anlamak için de bol bol soru çözümü yapmak da çok önemli. Çözemediğin sorulara yanıt bulmak istiyorsan sınava hazırlık sürecinde Kunduz hep yanında! Profesyonel eğitmenler tarafından hazırlanan Soru Çözümü, binlerce soru ve çözümden oluşan Soru Bankası hizmetlerimizden faydalanabilirsin.





