Mantık Nedir?
Mantık, bilginin yapısını inceleyen, doğru ile yanlış arasındaki akıl yürütmenin ayrımını yapan disiplindir. Önceleri bir felsefe dalıyken daha sonra kendi başına bir bilim dalı olmuştur. Matematik ve bilgisayar biliminin de parçası haline gelmiştir.
Önerme Nedir?
Doğruluğu veya yanlışlığı kesin hüküm bildiren ifadelere önerme denir. Önermeler kişiden kişiye değişmeyen ve kanıtlanabilen ifadelerdir. Soru, istek ve emir cümleleri önerme olamaz.
Örneğin;
“2’nin karesi 4’tür” cümlesi bir önermedir, çünkü doğruluğu kanıtlayabiliyoruz.
“Bir ay 25 gündür” cümlesi bir önermedir, çünkü yanlışlığını kanıtlayabiliyoruz.
“İyi geceler” ifadesi bir önerme değildir, çünkü doğru veya yanlış bir ifade belirtmez.
Önerme Türleri
- Basit Önerme
- Bileşik Önerme
- Denk Önermeler
- Koşullu Önerme
- Açık Önerme
Basit Önerme
Önermelerin doğruluk değeri D ve Y harfleri, 1 ve 0 sayıları ile belirtilir. Önerme doğru ise doğruluk değeri D veya 1, yanlış ise doğruluk değeri Y veya 0 olur. Bu önerme çeşileri tek yargı belirttiği için basit önermedir.
Bileşik Önerme
İki veya daha fazla önermenin “ve”, “veya”, “ya da”, “ise”, “ancak ve ancak” gibi bağlaçlar ile bağlanarak elde edilen önermeye bileşik önerme denir.
Örneğin;
“2 çift sayıdır”
“2 asal sayıdır”
önermelerini “ve” bağlacı ile bağlayarak “2 çift ve asal sayıdır” bileşik önermesini elde edebiliriz.
Denk Önermeler
Doğruluk değerleri aynı olan iki önermeye denk önermeler denir.

İki önermenin doğruluk değeri aynı ise biz bu önermelere denk önermeler deriz.
Örneğin;
p: Bir yıl 10 aydır.
q: Tam sayılar kümesi rasyonel sayılar kümesini kapsar.
p önermesi yanlış bir önerme olduğu için doğruluk değeri 0’dır.
Her rasyonel sayı bir tam sayı değildir, bu yüzden tam sayılar kümesi rasyonel sayılar kümesini kapsamaz. q önermesi yanlış bir önermedir.
p ve q önermelerinin doğruluk değeri eşit olduğu için denk önermeler diyebiliriz.
Koşullu Önerme
p ve q önermelerinin “ise” bağlacı ⟹ ile bağlanmasıyla oluşturulan bileşik önermeye koşullu önerme denir. İse bağlacı ile kurulan koşullu önermeler p ise q diye okunur.
Açık Önerme
İçinde en az bir değişken bulunan ve değişkenlere verilen değerlere göre doğru ya da yanlış olan önermelere açık önerme denir.
Açık önermeyi doğru yapan değerler kümesine açık önermenin doğruluk kümesi denir.
Bir Önermenin Değili (Olumsuzu)
Önermenin değili verilen önermenin olumsuzunu ifade eder.
p önermesinin değili p’ şeklinde gösterilir.
Örneğin;
“p: Ankara Türkiye’nin başkentidir” önermesi verilmiş olsun. Bu önermenin değili yani olumsuzu
“p’: Ankara Türkiye’nin başkenti değildir. “ şeklinde ifade edilir.
Önerme ve Doğruluk Değeri
Doğru ya da yanlış kesin hüküm bildiren ifadelere önerme denir. Önermeler genellikle p, q, r. s…. gibi küçük harflerle gösterilir. Eğer bir önerme doğru ise önermenin doğruluk değeri 1, yanlış ise doğruluk değeri 0 dir.
Önerme Denkliği
Doğruluk değerleri aynı olan önermelere denk (eşdeğer) önermeler denir.
Doğruluk Tablosu
| p | q | p /\ q | p \/ q | p => q | p <=> q |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 |
“veya (\/)” Bağlacının Özellikleri
- Tek kuvvet özelliği
- Değişme özelliği
- Birleşme özelliği
- Dağılma özelliği
Tek Kuvvet Özelliği
Bir önermenin kendisini ile “veya” bağlacı kullanarak kurulan bileşik önerme önermenin kendisine eşittir.
Değişme Özelliği

Birleşme Özelliği

Dağılma Özelliği

De Morgan Kuralları
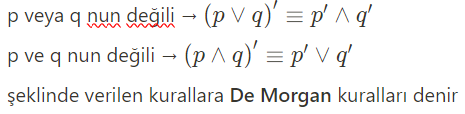
İse Bağlacı (=>)
p ile q önermesinin ise bağlacı ile bağlanarak oluşan bileşik önermeye koşullu önerme denir.
Koşullu önerme p => q şeklinde gösterilir.
p => q koşullu önermesi; p doğru q yanlış iken yanlış, diğer durumlarda ise doğrudur.
Ancak ve Ancak Bağlacı (<=>)
p ile q önermelerinin ancak ve ancak bağlacı ile bağlanarak elde edilen bileşik önermeye iki yönlü koşullu önerme denir.
p <=> q iki yönlü koşullu önermesi p ile q’nun doğruluk değeri denk iken doğru, farklı iken yanlıştır.
Her Niceleyicisi (Evrensel Niceleyici)
Önüne geldiği elamanların tamamını ifade eden niceleyiciye evrensel niceleyici denir.

Bazı Niceleyicisi
Bazı niceleyicisi bir kümenin en az bir elamanını ifade ettiği için her niceleyicisine varlıksal niceleyici denir.

İspat Yöntemleri
- Doğrudan ispat yöntemi
- Olmayana ergi yöntemi
- Aksine örnek yöntemi
- Çelişki yöntemi
Tanım, Aksiyom, Teorem ve İspat Kavramları
Bir teriminin özelliklerini tanımlı, tanımsız terimler kullanarak açıklayan ifadeye tanım denir.
İyi bir tanımda olması gereken özellikler;
Anlamı bilinen sözcükler, tanımlı ya da tanımsız terimler kullanılarak yapılır.
Anlaşılır, tutarlı ve kesin ifadeler kullanılmalıdır.
örneğin;
“1 ve kendisinden başka pozitif tam sayı böleni olmayan sayılara asal sayı nedir.”
Doğruluğu ispatlanamayan, ispata gerek duyulmaksızın doğruluğu kabul edilen önermelere aksiyom denir.
örneğin;
“İki noktadan bir doğru geçer.”
Doğruluğu ispatlanabilen önermelere teorem denir.
İspatlanmayan bir ifade matematiksel olarak doğru kabul edilmez. Matematiksek ispat önermedeki varsayımlardan yola çıkarak doğruluğu bilinen mantıksal çıkarımlar ile adım adım önermede iddia edilen sonuca ulaşma yoludur. Bunun için farklı ispat yöntemleri kullanılabilir.
Peki bu ispat yöntemleri nelerdir?
- Doğrudan ispat yöntemi
- Olmayana ergi yöntemi
- Aksine örnek yöntemi
- Çelişki yöntemi

