Vektör Nedir?
Bir sayı ve birimin yanında doğrultu, yön ve uygulama noktası da bilinen niceliklere vektör denir. Vektörler yönlendirilmiş doğru parçası şeklinde gösterilir.
Vektörel büyüklük kavramının tam olarak ifade edilmesi, dört niceliğinin belirtilmesi ile mümkündür:
- Başlangıç noktası (uygulama noktası)
- Doğrultusu
- Yönü
- Şiddeti (Büyüklüğü)
Vektörlerin Özellikleri
- Doğrultusu, yönü ve şiddeti aynı olan vektörlere eşit vektör denir.
- Yalnız yönü değişen vektörün işareti de değişir. Vektörel büyüklükler, başındaki (+) ve (-) işaretlerine göre yön belirtir. Büyüklüğü ve doğrultusu aynı yöne zıt olan vektörlere zıt vektör denir.
- Bir vektörün skaler bir sayı ile çarpımı ya da bölümü yine vektörel büyüklük olmaktadır. Vektörün başındaki skaler sayılar büyüklük belirtir.
- Bir vektör başka bir yere taşınırken yönü, doğrultusu, şiddeti değiştirilmez.
- İki vektörün toplamı ya da farkı yine bir vektördür.
- Vektörlerde toplamada değişme özelliği vardır.
Vektörlerin Toplanması
Vektörlerin toplanması üç yöntemle olur. Bunlar:
- Paralel kenar metodu
- Uç uca ekleme metodu
- Bileşenlere ayırma metodu
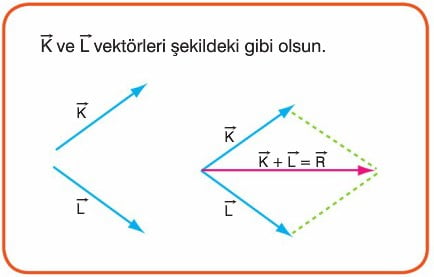
Paralel Kenar Metodu
Başlangıç noktası aynı olan vektörler paralel kenara tamamlanır. Başlangıç noktası ile kesim noktasını birleştiren vektör, toplam vektörü verir.
İkiden fazla vektörün toplanması paralel kenar metoduna göre yapılırken önce rastgele iki vektörün toplamı yapılır, sonra toplam vektör ile diğer vektör paralel kenar metoduna göre yapılarak işlem devam ettirilir.
Uç Uca Ekleme Metodu
Vektörler den biri rastgele seçilip diğer vektörlerin doğrultusu, yönü ve şiddeti değiştirilmeden sıra ile ucuca eklenir. Birinci vektörün başlangıç noktası ile son vektörün ucuna doğru toplam vektör çizilir.

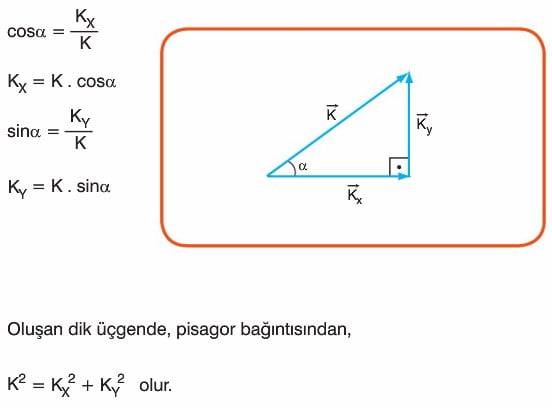
Bileşenlere Ayırma Metodu
Bir vektörün bileşenleri o vektörün x ve y düzlemlerindeki izdüşümüdür.
Eşit Vektörler
Eğer iki vektörün doğrultusu, yönü ve büyüklüğü aynı ise bunlara eşit vektörler ya da özdeş vektörler denir. Eşit vektörlerin uygulama noktaları farklı olabilir.
Zıt Vektörler
Eğer iki vektörün doğrultuları ve büyüklükleri aynı ama yönleri zıt ise bunlara zıt vektörler denir. Zıt vektörlerin de uygulama noktaları farklı olabilir.
Vektörün Skalerle Çarpımı
Bir vektörü pozitif skaler bir nicelikle (yani sayıyla çarpmak) vektörün büyüklüğünü çarpıldığı sayıyla orantılı olarak değiştirir.
Vektörler ve Kartezyen Koordinat Düzleminde Gösterilmesi
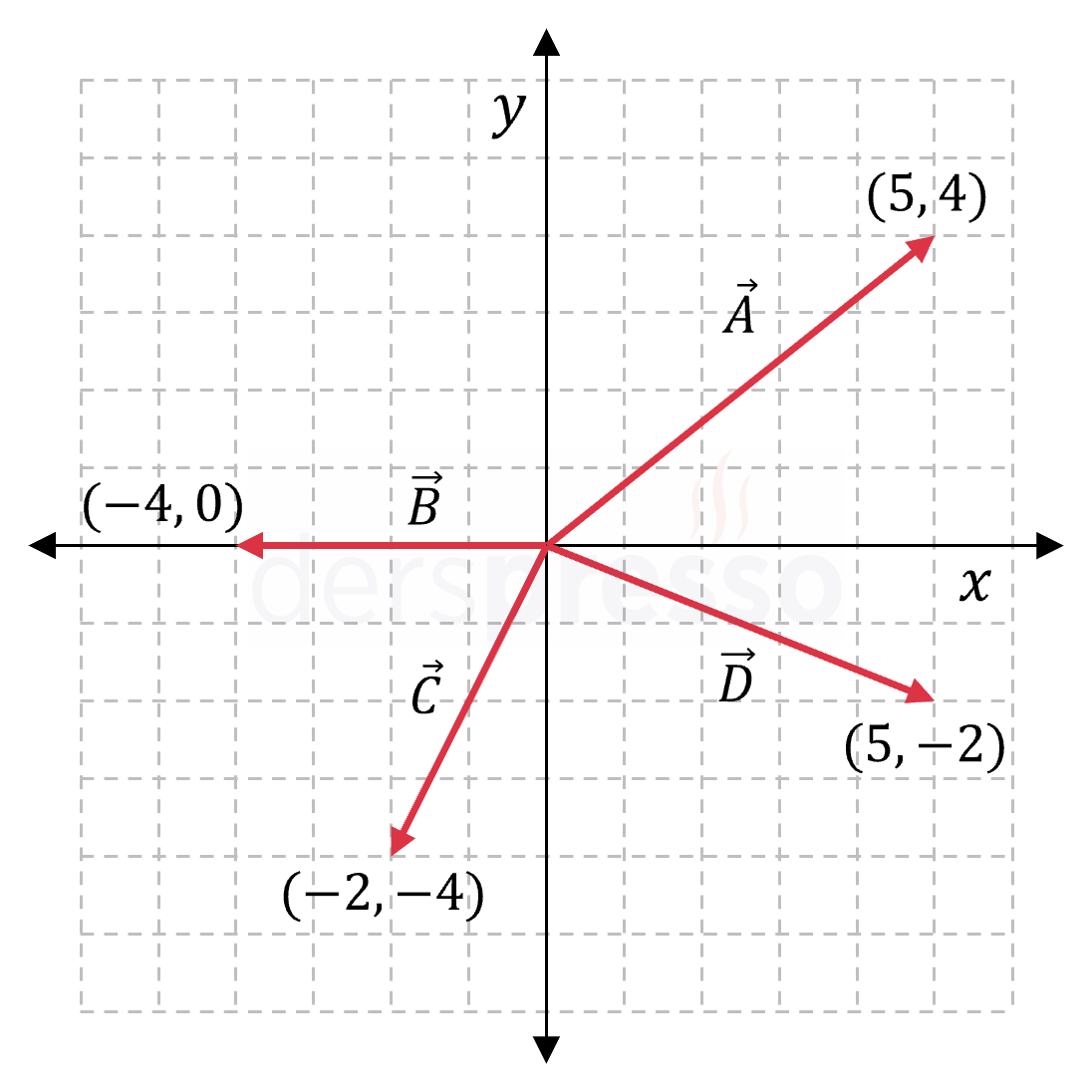
Fizik biliminin pek çok dalı, uzaydaki yerleşim düzeniyle ilgilenir. Bir cismin hareketini matematiksel olarak açıklayabilmek için, o cismin konumunu tanımlamak gerekir. Bu tanımlama koordinat sisteminin kullanılması ile sağlanır. Yatay ve düşey eksenlerin kesiştiği noktanın orijin olarak alındığı koordinat sistemine “kartezyen koordinat sistemi” ya da “dik koordinat sistemi” denir. Bir vektörü, iki boyutlu dik koordinat sisteminde göstermek için vektörün bitiş noktasının (x,y) koordinatı belirtilir ve orijinden o noktaya ok çizilir.
Vektörlere Özel Durumlar
- Aynı yöndeki vektörlerin bileşkesi, büyüklüklerin toplamına eşittir.
- Zıt yöndeki vektörlerin bileşekesi, vektörlerin büyüklüklerinin farkına eşittir.
- Aralarındaki açı 60ᵒ olan eşit büyüklükteki vektörlerin bileşkesinin büyüklüğü, vektörlerden birinin büyüklüğünün √3 katıdır.
- Aralarındaki açı 90ᵒ olan vektörlerin bileşkesinin büyüklüğü Pisagor ile bulunur.
- Aralarındaki açı 120ᵒ olan eşit büyüklükteki vektörlerin bileşkesinin büyüklüğü vektörlerden birinin büyüklüğüne eşittir.
Bileşke Vektörler ve Kosinüs Teoremi
Büyüklükleri F1 ve F2 olan iki vektör arasında α kadar açı varsa, bileşke vektörün büyüklüğü:
R2 = F12+ F22 + 2. F1.F2.cosα bağıntısı ile hesaplanır. Kosinüs Teoremi sayesinde bu eşitliği elde ederiz.
- Bileşke vektör, büyük vektöre daha yakındır.
- İki vektörün bileşkesinin en büyük değeri vektörler aynı yönde iken elde edilir. En büyük bileşke, vektörlerin büyüklüklerinin toplamına eşittir.
- İki vektörün bileşkesin en küçük değeri vektörler zıt yönde iken elde edilir. En küçük bileşke, vektörlerin büyüklüklerinin farkına eşittir.
- A+B ≥ R ≥ |A-B|
- İki vektörün arasındaki açı arttıkça bileşke azalır.

