Welcome to our comprehensive guide on acute angles! In this article, we will delve into the definition, formula, degrees, images, applications, and examples of acute angles. Whether you’re a math enthusiast, a student, or simply curious about geometry, this guide will provide you with a thorough understanding of acute angles. So let’s dive in!
An Introduction to the Acute Angle
In the world of geometry, angles play a fundamental role. An angle is formed when two rays meet at a common endpoint, known as the vertex. The measure of an angle determines its classification. One such classification is the acute angle.
What is an Angle?
Before we explore acute angles in detail, let’s briefly understand what an angle is. An angle is a geometric figure formed by two rays or line segments that share a common endpoint called the vertex. The rays or line segments are known as the arms of the angle. Angles are measured in degrees using a protractor.
What is the Acute Angle?
An acute angle is an angle that measures less than 90 degrees. The term “acute” originates from the Latin word “acutus,” which means “sharp” or “pointed.” This terminology refers to the sharpness or narrowness of the angle. In other words, an acute angle is “sharp” or “narrow,” with its two arms meeting at a point that is less than a right angle.
Acute Angle Degree
The degree of an acute angle is always less than 90 degrees. Examples of acute angles include 30 degrees, 45 degrees, 60 degrees, and 75 degrees. These angles are all considered acute because they are smaller than a right angle. An acute angle can be represented in degrees using the symbol “°”.
Acute Angle Images
To visualize acute angles, let’s take a look at some images. In the first image, an angle measuring 40 degrees is depicted. The second image shows an angle measuring 60 degrees. These images help us understand the concept of acute angles visually, emphasizing their sharpness and narrowness.

Acute Angle Formula
The formula to determine if an angle is acute involves comparing its measure to 90 degrees. If the measure of an angle is less than 90 degrees, it is classified as acute. Mathematically, the formula can be expressed as:
Angle Measure < 90°
This formula allows us to quickly identify whether an angle is acute or not by comparing its measure to the right angle.
Acute Angle Triangle
An acute triangle is a type of triangle where all three interior angles are acute angles, meaning they measure less than 90 degrees. In other words, the angles of an acute triangle are “sharp” or “narrow.” Examples of acute triangles include equilateral triangles, where all three angles measure 60 degrees, and scalene triangles with three different acute angles.
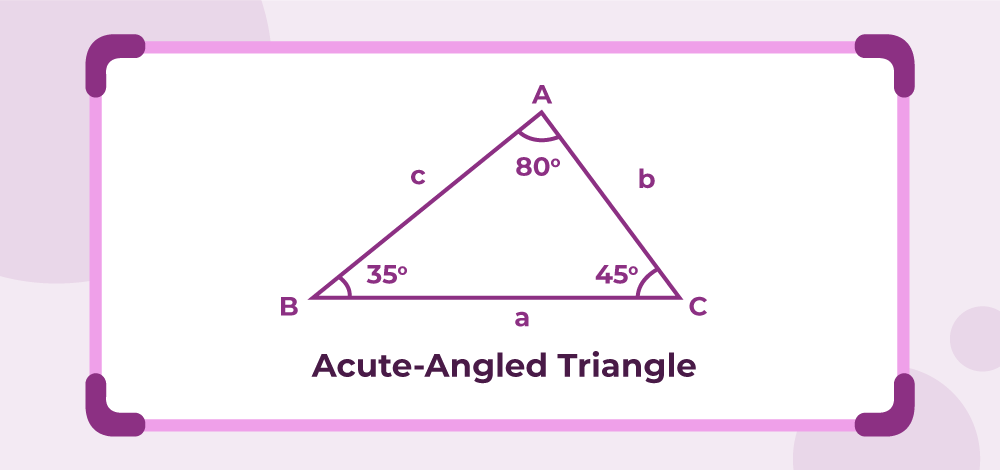
Properties of Acute Triangles
Acute triangles possess several interesting properties. Let’s explore some of them:
- The sum of the interior angles of an acute triangle is always 180 degrees.
- The sides of an acute triangle satisfy the following inequalities:
- a² + b² > c²
- b² + c² > a²
- c² + a² > b² where a, b, and c represent the lengths of the sides of the triangle.
These properties help us identify and analyze acute triangles, providing valuable insights into their geometric characteristics.
Shapes of Acute Angles
Acute angles can be found in various geometric shapes. Let’s explore two common shapes where acute angles are present:
Acute Angle Parallelogram
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. In a parallelogram, two pairs of opposite angles are congruent, meaning they have the same measures. Therefore, a parallelogram contains two acute angles and two obtuse angles.
Acute Angle Trapezoid
A trapezoid is a quadrilateral with only one pair of opposite sides that are parallel. In a trapezoid, the non-parallel sides are called legs, while the parallel sides are called bases. An acute trapezoid is a trapezoid where both interior angles created by the longer base and the legs are acute angles.
Acute Angle vs. Obtuse Angle
Now, let’s compare acute angles with another type of angle called an obtuse angle. An obtuse angle is an angle that measures greater than 90 degrees but less than 180 degrees. In contrast, an acute angle measures less than 90 degrees. The following table summarizes the differences between acute and obtuse angles:
| Acute Angle | Obtuse Angle |
|---|---|
| Measures less than 90 degrees | Measures more than 90 degrees but less than 180 degrees |
| Appears sharp or narrow | Appears wide or broad |
| Common in various geometric shapes | Less common in geometric shapes |
As illustrated in the table, acute angles are “sharp” or “narrow” angles, while obtuse angles are “blunt” or “wide” angles. The distinction between these two types of angles is based on their measurements.
Types of Angles
Angles can be classified into several types based on their measurements. Let’s explore some of the major types:
- Acute Angle: An angle that measures less than 90 degrees.
- Right Angle: An angle that measures exactly 90 degrees.
- Obtuse Angle: An angle that measures greater than 90 degrees but less than 180 degrees.
- Straight Angle: An angle that measures exactly 180 degrees.
- Reflex Angle: An angle that measures greater than 180 degrees but less than 360 degrees.
- Complete Angle: An angle that measures exactly 360 degrees.
These types of angles provide a framework for understanding and categorizing various angle measurements.
Solved Examples on Acute Angle
To further solidify our understanding of acute angles, let’s work through some solved examples:
Example 1: Find the measure of an angle that is one-fourth of a right angle.
Solution: A right angle measures 90 degrees. To find one-fourth of a right angle, we divide 90 by 4:
90° / 4 = 22.5°
Therefore, the measure of the angle is 22.5 degrees.
Example 2: Determine whether an angle measuring 100 degrees is acute or obtuse.
Solution: An acute angle measures less than 90 degrees. Since 100 degrees is greater than 90 degrees, the angle is not acute. Instead, it is classified as an obtuse angle.
These examples showcase how we can apply our knowledge of acute angles to solve real-world problems.
How Kunduz Can Help You Learn Acute Angles?
At Kunduz, we understand the importance of mastering mathematical concepts like acute angles. That’s why we offer a wide range of resources and educational materials to help you learn and excel in geometry. Our experienced teachers and comprehensive curriculum provide step-by-step guidance, ensuring a solid foundation in acute angles and other mathematical topics.
Join Kunduz today and embark on an exciting learning journey that will empower you with the knowledge and skills to tackle any geometry challenge!
