In the realm of algebra, a binomial is defined as a polynomial with two terms that are being summed together. It is a fundamental concept that plays a crucial role in various mathematical and statistical applications. Understanding the properties and operations of binomials is essential in solving equations, performing calculations, and analyzing data.
What is a Binomial?
A binomial is a specific type of polynomial that consists of two terms connected by either addition or subtraction. Each term in a binomial can contain variables, constants, coefficients, and exponents. The terms are separated by arithmetic operators, such as “+” for addition and “-” for subtraction. The simplest form of a binomial is expressed as ax + b, where “a” and “b” represent coefficients and “x” represents a variable.
What are Polynomials?
Before delving deeper into binomials, it is important to have a clear understanding of polynomials. A polynomial is an algebraic expression that consists of one or more terms. These terms can contain variables, constants, coefficients, and exponents. Polynomials are categorized based on the number of terms they contain, such as monomials (one term), binomials (two terms), trinomials (three terms), and polynomials (more than three terms).

Examples of Binomial
To further illustrate the concept of binomials, let’s consider some examples:
- 3x + 2y: In this binomial, the terms are 3x and 2y, with “3” and “2” as coefficients and “x” and “y” as variables.
- 5a2 – 7b: This binomial consists of the terms 5a2 and -7b, with “5” and “-7” as the coefficients and “a” and “b” as the variables.
- x + y: Here, the terms are x and y, with “1” as the coefficient for both terms.
Types of Algebraic Expressions
Algebraic expressions can be categorized into different types based on the number of terms they contain. These types include monomials, binomials, trinomials, polynomials, and multinomials.
Monomial
A monomial is an algebraic expression that consists of only one term. It can contain variables, constants, coefficients, and exponents. Some examples of monomials are 3x, 2y2, and 5xy.
Binomial
A binomial is an algebraic expression that consists of two terms. These terms can contain variables, constants, coefficients, and exponents. Examples of binomial expressions include 4×2 – 3y, 2a + 5b, and x2 + 2x.
Trinomial
A trinomial is an algebraic expression that consists of three terms. It follows the same pattern as a binomial, but with an additional term. Examples of trinomial expressions include 2×3 + 3×2 – 4x, y2 + 5y – 1, and 3a + 2b – c.
Polynomial
A polynomial is an algebraic expression that consists of one, two, or more terms. It is a general term that encompasses monomials, binomials, and trinomials. Examples of polynomial expressions include 2×4 + 3×2 – 5, 4a3 – 2a2 + 7a – 1, and x5 – 5×3 + 4×2 – 2x.
Multinomial
A multinomial is an algebraic expression that consists of more than three terms. It is an extension of the polynomial concept and can contain any number of terms. Examples of multinomial expressions include 2×5 – 3×3 + 4×2 – 5x + 1, 3a4 – 2a3 + 7a2 – 4a + 5, and x6 – 5×4 + 2×3 – 3×2 + 4x – 1.
Binomial Coefficient
The binomial coefficient is a positive integer that represents the coefficient of terms in a binomial expansion. It is derived from the binomial theorem, which expands the expression (a + b)n or (x + y)n. The binomial coefficient is denoted as nCk, where “n” represents the power of the binomial and “k” represents the term number in the expansion. The formula to calculate the binomial coefficient is:
nCk = n! / (k! * (n – k)!)
Here, “!” denotes the factorial of a number. The binomial coefficient represents the number of ways to choose k items from a set of n items. For example, in the expansion of (x + 1)3, the binomial coefficients are 1, 3, 3, and 1.
Binomial Equation
A binomial equation is an equation that contains one or more binomials. It can be a simple equation with two binomial expressions or a more complex equation with multiple binomials. Solving binomial equations involves various algebraic techniques, such as factoring, expanding, and simplifying the expressions. The solutions to the equation are the values of the variables that make the equation true.
Operations on Binomials
Binomials can undergo various operations, including factorization, addition, subtraction, multiplication, raising to the nth power, and converting to lower-order binomials. These operations allow us to manipulate binomials and solve equations involving binomials.
Factorization
Factorization is the process of expressing a binomial as a product of its factors. It involves finding the common factors between the terms of the binomial and rewriting it in a simplified form. Factorization is useful in simplifying expressions, solving equations, and factoring quadratic equations.
Addition
Adding binomials involves combining like terms by adding the coefficients of the corresponding terms. Only terms with the same variables and exponents can be added. The result is a new binomial expression with simplified terms.
Subtraction
Subtracting binomials follows the same principle as addition, but instead of adding the coefficients, we subtract them. Again, only terms with the same variables and exponents can be subtracted. The result is a new binomial expression with simplified terms.
Multiplication
Multiplying binomials requires the application of the distributive property. Each term of the first binomial is multiplied by each term of the second binomial, resulting in four terms. Simplification is then done by combining like terms.
Raising to nth Power
Raising a binomial to the nth power involves expanding the binomial using the binomial theorem. The binomial theorem provides a formula for expanding (a + b)n, where “n” represents the power and “a” and “b” represent the terms of the binomial. The expansion results in a series of terms, each with a specific coefficient and power of the terms.
Converting to Lower-Order Binomials
Converting a higher-order binomial to lower-order binomials involves factoring out common terms or applying specific identities, such as the difference of squares or the sum of cubes. By simplifying a binomial, we can express it as a product of binomials with lower powers.
Binomial Expansion
Binomial expansion is the process of expanding a binomial expression raised to a power. It involves applying the binomial theorem to find the coefficients and powers of the terms in the expansion. The binomial theorem provides a formula for expanding (a + b)n, where “n” represents the power and “a” and “b” represent the terms of the binomial.
Binomial Formula
The binomial formula is an algebraic formula that calculates the value of a binomial coefficient. It is derived from the binomial theorem and provides a direct way to calculate the binomial coefficient without expanding the entire binomial expression. The formula for the binomial coefficient is:
nCk = n! / (k! * (n – k)!)
This formula allows us to find the number of ways to choose k items from a set of n items, without having to expand the entire binomial expression.
Binomial Distribution
The binomial distribution is a probability distribution that models the number of successes in a fixed number of independent Bernoulli trials. It is characterized by two parameters: the number of trials “n” and the probability of success “p” for each trial. The binomial distribution is widely used in statistics and probability theory to analyze and predict the outcomes of binary experiments.
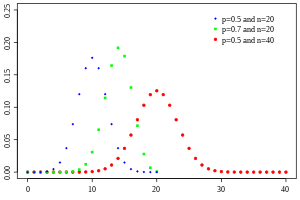
Properties of Binomial
The binomial distribution has several important properties that make it useful in practical applications. These properties include the expected value, variance, higher moments, mode, median, and tail bounds. Understanding these properties allows us to make predictions and draw conclusions based on the binomial distribution.
Expected Value and Variance
The expected value of a binomial distribution is the mean or average number of successes in a fixed number of trials. It is calculated by multiplying the number of trials “n” by the probability of success “p”. The variance measures the spread or dispersion of the distribution and is calculated by multiplying the number of trials “n” by the probability of success “p” and the probability of failure “1-p”.
Higher Moments
The higher moments of a binomial distribution measure additional properties of the distribution, such as skewness and kurtosis. These moments provide insights into the shape and symmetry of the distribution.
Mode
The mode of a binomial distribution is the value or values that occur with the highest frequency. In the case of a binomial distribution, the mode is the most probable number of successes in a fixed number of trials.
Median
The median of a binomial distribution is the middle value that separates the lower and upper halves of the distribution. It represents the value that is equally likely to be above or below the median.
Tail Bounds
Tail bounds provide upper and lower bounds for the probabilities in the tails of the binomial distribution. These bounds are useful for estimating the likelihood of extreme events or rare occurrences.
How Kunduz Can Help You Learn Binomials?
Kunduz is a comprehensive online learning platform that offers a wide range of educational resources and interactive lessons to help students learn and understand binomial distributions. Through engaging tutorials, practice problems, and real-world examples, Kunduz provides a supportive learning environment that caters to individual needs and promotes academic success. Whether you are a beginner or an advanced learner, Kunduz has the tools and resources to help you master the concepts of binomial distributions and excel in your studies.
By utilizing Kunduz’s user-friendly interface and expertly designed curriculum, students can easily grasp the fundamental principles of binomial distributions and confidently apply them to various mathematical and statistical problems. With Kunduz, learning about binomial distributions becomes an enjoyable and rewarding experience, enabling students to develop a solid foundation in mathematics and statistics.
