Change of Base Formula: What Is Change of Base Formula? Concepts and Derivation

As mathematics students, you may have noticed that our scientific calculators have “log” and “ln” buttons but rarely a logarithmic key for different bases. Yet, logarithmic problems often involve bases other than 10 and e. How, then, do we calculate logarithms with different bases? This is where the change of base formula comes into play. This mathematical tool is indispensable for understanding and solving a range of logarithmic problems. In this comprehensive guide, we will delve into the concepts, derivation, and applications of the change of base formula.

An Introduction to Change of Base Formula

Logarithms and their bases are fundamental components of mathematical calculations. However, most scientific calculators only offer options for logarithms with bases 10 (log) and e (ln). The change of base formula is a crucial tool that enables us to calculate logarithms with bases other than 10 and e. This formula is a property of logarithms and is widely used for the simplification and solving of logarithmic problems.

What is Change of Base Formula?

The change of base formula is a mathematical rule that allows us to express a logarithm in one base as a logarithm in another base. It is an effective method to rewrite a logarithm of a number with a given base as the ratio of two logarithms, each with a different base than the original logarithm. This formula is the key to changing the base of a logarithm, making it easier to work with and evaluate.

The change of base formula can be represented as follows:

log_ba = log_ca / log_cb

In this formula:

The argument of the logarithm in the numerator is the same as the argument of the original logarithm.
The argument of the logarithm in the denominator matches the base of the original logarithm.
Both logarithms in the numerator and denominator must share the same base, which can be any positive number other than 1.

A variant of this formula is also used extensively in solving logarithmic problems:

log_ba · log_cb = log_ca

Change of Base Formula Derivation

The change of base formula seems deceptively simple, but it’s based on the fundamental properties of logarithms. Let’s delve into the steps involved in deriving this formula.

Let’s assume that log_ba = p, log_ca = q, and log_cb = r. When we convert these to their exponential forms, we get a = b^p, a = c^q, and b = c^r.

From the first two equations, we have b^p = c^q. Substituting b = c^r (which is from the third equation) here, we get:

(c^r)^p = c^q

Applying the property of exponents, a^mn = a^mn, we obtain:

c^rp = c^q

This leads us to pr = q, and then p = q / r.

Substituting the values of p, q, and r, we arrive at the change of base formula:

log_ba = log_ca / log_cb

Log Change of Base Formula Proof

While the derivation gives us an intuitive understanding of the formula, its formal proof provides a more rigorous foundation.

Assume log_ba = p, log_ca = q, and log_cb = r. Converting these into exponential form, we get a = b^p, a = c^q, and b = c^r.

From the first two equations, we have b^p = c^q. Substituting b = c^r (from the third equation) into this, we get:

(c^r)^p = c^q

By leveraging the property of exponents, a^mn = a^mn, we obtain:

c^rp = c^q

This implies that pr = q, and consequently, p = q / r.

Substituting the values of p, q, and r, we arrive at the log change of base formula:

log_ba = log_ca / log_cb

Properties of Log Change of Base Formula

The change of base formula, log_ba = log_ca / log_cb, has some key properties:

It allows us to convert logarithms from one base to another, making calculations simpler.
The formula is applicable only to logarithms with positive bases.
Both the numerator and denominator of the formula represent logarithms with the same base c.
The formula can be used to simplify complex logarithmic expressions.

Applications of Log Change of Base Formula

The change of base formula is a versatile tool with a multitude of applications:

Solving exponential equations: The formula allows us to convert exponential equations with different bases into a common base, simplifying the equation and making it easier to solve for the unknown variable.
Calculating logarithmic values: At times, we need to evaluate logarithmic functions with different bases. The change of base formula allows us to convert these functions into a base that is easier to work with.
Simplifying expressions: The formula can be used to simplify expressions involving logarithms with different bases.
Converting between different units: In certain scientific applications, we may need to convert between different units of measurement that use logarithmic scales. The change of base formula allows us to do this.
Financial calculations: The formula is also used in finance to calculate interest rates, loan payments, and other financial quantities expressed using logarithmic scales.

How to Change the Base of a Log?

When it comes to changing the base of a logarithm, it’s a straightforward process. We can use the change of base formula, log_ba = log_ca / log_cb, to rewrite a logarithm with base b as a logarithm with base c. Here are the steps:

Start by writing the logarithm as a ratio of two logarithms with base c.
In the numerator, write the logarithm of the original argument with base c.
In the denominator, write the logarithm of the original base with base c.
Simplify the ratio if possible or evaluate it using a calculator.

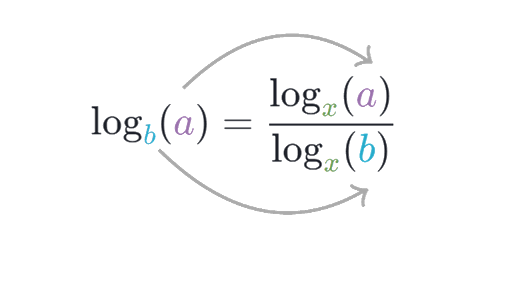
Solved Examples on Change of Base Formula

Let us solve a few examples to understand the application of the change of base formula better:

Example 1: Evaluate the value of log₆₄8 using the change of base formula.

Solution:

We will apply the change of base formula (by changing the base to 10). Note that log₁₀ is the same as log.

log₆₄8 = log₁₀8 / log₁₀64 = log 8 / log 64 = log 8 / log 8² = log 8 / 2 log 8 = 1 / 2

So, log₆₄8 = 1/2.

Example 2: Calculate log₉8.

Solution:

We cannot calculate log₉8 directly, so we apply the change of base formula to change the base to 10 so it can be calculated easily.

log₉8 = log₁₀8 / log₁₀9 = log 8 / log 9 ≈ 0.903 / 0.954 ≈ 0.946

So, log₉8 ≈ 0.946.

Example 3: Evaluate the value of log₃2 · log₄3 · log₅4.

Solution:

Here, we have to use the change of base formula in the multiplication form which is, log_ba · log_cb = log_ca. We apply this formula twice to evaluate the given logarithmic expression.

log₃2 · log₄3 = log₄2

Substituting this value in the given expression, we get:

log₄2 · log₅4 = log₅2

Therefore, log₃2 · log₄3 · log₅4 = log₅2.

How Kunduz Can Help You Learn Change of Base Formula?

While the change of base formula is an essential tool in mathematics, understanding and applying it can be challenging for many students. Kunduz is an efficient and reliable learning platform that provides comprehensive and clear explanations of the change of base formula and its applications. By using Kunduz, you can gain a deep understanding of this formula and enhance your problem-solving skills in logarithms. With Kunduz, mastering the change of base formula is within your reach!