Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. One of the fundamental concepts in trigonometry is the half angle formula. In this article, we will explore the derivation of the half angle formula and discuss its various identities.
An Introduction to Half Angle Formula
In trigonometry, the half angle formula is used to find the values of trigonometric ratios for angles apart from the well-known values of 0°, 30°, 45°, 60°, 90°, and 180°. It allows us to determine the exact values of trigonometric functions for angles such as 15°, 22.5°, and others.
What is a Half Angle?
A half angle is simply half of a given angle. For example, if we have an angle of 60°, its half angle would be 30°. Half angles are derived from double angle formulas, which are in turn derived from the angle sum and difference formulas of trigonometry.
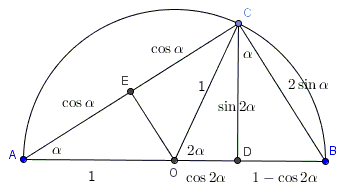
What is the Half Angle Formula?
The half angle formula is a trigonometric identity that relates the trigonometric functions of a given angle to the trigonometric functions of its half angle. There are three main half angle formulas: one for sine, one for cosine, and one for tangent.
Half Angle Formulas
Half Angle Formulas Derivation Using Double Angle Formulas
The half angle formulas can be derived using the double angle formulas. The double angle formulas for sine, cosine, and tangent are as follows:
- sin 2x = 2 sin x cos x
- cos 2x = cos² x – sin² x
- tan 2x = 2 tan x / (1 – tan² x)
By substituting x with x/2 in the above formulas, we can derive the half angle formulas:
- sin(x/2) = ± [(1 – cos x)/2]^1/2
- cos(x/2) = ± [(1 + cos x)/2]^1/2
- tan(x/2) = (1 – cos x)/sin x
Half Angle Formula for Sine Function
To derive the half angle formula for the sine function, we start with the double angle formula for cosine:
cos 2θ = 1 – 2sin² θ
By substituting θ with θ/2, we get:
cosθ = 1 – 2sin² (θ/2)
Solving for sin (θ/2), we have:
sin² (θ/2) = (1 – cosθ)/2
Taking the square root of both sides, we obtain the half angle formula for sine:
sin (θ/2) = ± [(1 – cosθ)/2]^1/2
Half Angle Formula for Cosine Function
To derive the half angle formula for the cosine function, we start with the double angle formula for cosine:
cos 2θ = 2cos² θ – 1
By substituting θ with θ/2, we get:
cosθ = 2cos² (θ/2) – 1
Solving for cos (θ/2), we have:
cos² (θ/2) = (1 + cosθ)/2
Taking the square root of both sides, we obtain the half angle formula for cosine:
cos (θ/2) = ± [(1 + cosθ)/2]^1/2
Half Angle Formula for Tangent Function
To derive the half angle formula for the tangent function, we start with the formula:
tan θ = sin θ / cos θ
By substituting θ with θ/2 and using the half angle formulas for sine and cosine, we get:
tan (θ/2) = sin (θ/2) / cos (θ/2)
Substituting the half angle formulas for sine and cosine, we obtain the half angle formula for tangent:
tan (θ/2) = (1 – cosθ)/sinθ
Half Angle Formula Using Semiperimeter
Another way to derive the half angle formulas is by using the semiperimeter of a triangle. Let’s consider a triangle ABC with sides a, b, and c and semiperimeter s.
The half angle formulas in terms of the sides of a triangle are as follows:
- sin (A/2) = √[(s – b) (s – c)/bc]
- cos (A/2) = √[s (s – a)/bc]
- tan (A/2) = √[(s – b) (s – c)/bc] / √[s (s – a)/bc]
These formulas allow us to find the values of trigonometric functions for half angles using the side lengths of a triangle.
Half Angle Identities
The half angle formulas give rise to various half angle identities. These identities are useful in solving trigonometric equations and proving trigonometric identities. Here are some of the half angle identities derived from the formulas:
- sin² (θ/2) + cos² (θ/2) = 1
- 1 + tan² (θ/2) = sec² (θ/2)
These identities can be used to simplify trigonometric expressions and solve equations involving half angles.
Double‐Angle and Half‐Angle Identities
The double-angle and half-angle identities are closely related and can be derived from each other. The double-angle identities are derived by substituting θ with 2θ in the half angle formulas, while the half-angle identities are derived by substituting θ with θ/2 in the double-angle formulas.
The double-angle identities for sine, cosine, and tangent are as follows:
- sin 2θ = 2 sin θ cos θ
- cos 2θ = cos² θ – sin² θ
- tan 2θ = 2 tan θ / (1 – tan² θ)
By substituting θ with θ/2 in the double-angle identities, we can derive the half-angle identities.
How to Use the Half-Angle Formula to Solve Equations
The half-angle formula can be used to solve trigonometric equations involving half angles. To solve an equation using the half-angle formula, follow these steps:
- Identify the equation that needs to be solved.
- Apply the half-angle formula to express the trigonometric function in terms of the half angle.
- Simplify the equation using algebraic manipulations.
- Solve the resulting equation for the half angle.
- Use the relationship between the half angle and the original angle to find the solutions to the equation.
Solved Examples on Half Angle Formula
Let’s work through a few examples to illustrate how the half-angle formula can be used to find the values of trigonometric functions for half angles.
Example 1: Find the value of sin (15°).
Solution: Using the half-angle formula for sine, we have:
sin (15°) = ± [(1 – cos 30°)/2]^1/2
sin (15°) = ± [(1 – √3/2)/2]^1/2
sin (15°) = ± [(2 – √3)/4]^1/2
Therefore, the value of sin (15°) is ± [(2 – √3)/4]^1/2.
Example 2: Find the value of cos (22.5°).
Solution: Using the half-angle formula for cosine, we have:
cos (22.5°) = ± [(1 + cos 45°)/2]^1/2
cos (22.5°) = ± [(1 + √2/2)/2]^1/2
cos (22.5°) = ± [(2 + √2)/4]^1/2
Therefore, the value of cos (22.5°) is ± [(2 + √2)/4]^1/2.
Example 3: Find the value of tan (30°).
Solution: Using the half-angle formula for tangent, we have:
tan (30°) = (1 – cos 60°)/sin 60°
tan (30°) = (1 – 1/2)/(√3/2)
tan (30°) = (1/2)/(√3/2)
tan (30°) = 1/√3
Therefore, the value of tan (30°) is 1/√3.
How Kunduz Can Help You Learn Half Angle Formula?
Kunduz is an online learning platform that provides comprehensive resources and tutorials to help students learn and understand various mathematical concepts, including the half angle formula. With Kunduz, you can access step-by-step explanations, solved examples, practice problems, and interactive quizzes to test your knowledge and reinforce your understanding of the half angle formula. Whether you need assistance with homework or want to improve your math skills, Kunduz is here to support you on your learning journey.
If you want to learn more trigonometry information, you can also visit our Pythagorean theorem and Differentiation of Trigonometric Functions pages.
