The gas constant, also known as the ideal gas constant or universal gas constant, plays a crucial role in the study of gases in physics and chemistry. It is denoted by the symbol R and is expressed in units of energy per temperature increment per mole. The gas constant value is equivalent to the Boltzmann constant, but it is expressed as the pressure-volume product instead of energy per increment of temperature per particle.
Gases are one of the most important states of matter, known for their high compressibility and the ability to uniformly distribute pressure on all sides. They have no definite shape or volume, instead adapting to the shape of the container they occupy. Gases are also highly miscible, as there is negligible interaction between intermolecular forces.
To understand the behavior of gases under different conditions, several laws have been formulated based on experimental studies. These laws govern the characteristic traits of all gases and are fundamental to understanding the gas constant.
What is the Ideal Gas Constant?
The ideal gas constant, denoted by R, is a proportionality constant used to relate the energy scale to the temperature scale when considering one mole of particles at a defined temperature. It is the combination of Boyle’s law, Avogadro’s number, Charles’s law, and Gay-Lussac’s law. The ideal gas constant is a physical constant that appears in many fundamental equations in the physical sciences.
In the ideal gas law, which is a combination of Boyle’s law, Charles’s law, and Avogadro’s law, the gas constant plays a crucial role. The ideal gas law is expressed as PV = nRT, where P is the pressure, V is the volume, n is the number of moles, T is the temperature, and R is the gas constant.
The gas constant can also be found in the Nernst equation, which relates the reduction potential of a half-cell to the standard electrode potential. The gas constant is a fundamental factor in numerous principles and laws of physics, serving as a key component in various equations.

What is the Value of R in Atm?
The value of the gas constant depends on the units used for pressure, volume, and temperature. Prior to 2019, the common value for the gas constant in atm was R = 0.0821 liter·atm/mol·K. However, after the redefinition of SI base units in 2019, the gas constant now has an exact value of R = 8.31446261815324 J·K−1·mol−1.
The gas constant can be expressed in various units, depending on its application. Some of the gas constant values in different units are as follows:
| Gas Constant Value | Units |
|---|---|
| 8.3144598(48) | J⋅K−1⋅mol−1 |
| 8.3144598(48)×10^3 | amu·m²·s⁻²·K⁻¹ |
| 8.3144598(48)×10^−2 | L·bar·K⁻¹·mol−1 |
| 8.3144598(48) | m^3·Pa·K⁻¹·mol−1 |
| 162.363577(36) | L·Torr·K⁻¹·mol−1 |
| 11.9872036(11)×10^−3 | kcal·K⁻¹·mol−1 |
| 8.2057338(47)×10^−5 | m^3·atm·K⁻¹·mol−1 |
| 0.082057338(47) | L·atm·K⁻¹·mol−1 |
Gas Constant Value
The gas constant, also known as the ideal gas constant or universal gas constant, is a physical constant that appears in many fundamental equations in the physical sciences. Its value depends on the units used for pressure, volume, and temperature.
The gas constant value is R = 8.3144598(48) J⋅K−1⋅mol−1. The digits inside the parentheses represent the uncertainty in the measurement of the gas constant value. This value is based on the redefined SI base units, which were implemented in 2019.
The gas constant can be expressed in various units, such as amu·m²·s⁻²·K⁻¹, L·bar·K⁻¹·mol−1, m^3·Pa·K⁻¹·mol−1, L·Torr·K⁻¹·mol−1, kcal·K⁻¹·mol−1, m^3·atm·K⁻¹·mol−1, and L·atm·K⁻¹·mol−1. These different units allow for the gas constant to be used in diverse applications across different scientific disciplines.
Specific Gas Constant
The specific gas constant, denoted as Rspecific, is the ratio of the molar gas constant (R) to the molar mass (M) of a gas or gas mixture. It is a property specific to a particular gas or mixture.
Mathematically, the specific gas constant can be expressed as:
Rspecific = R/M
The specific gas constant is a useful quantity in various applications, as it allows for calculations specific to a particular gas or mixture. By dividing the molar gas constant by the molar mass, scientists and engineers can obtain a value that is tailored to the specific properties of the gas or mixture they are working with.

Dimensions
The gas constant (R) can be expressed in terms of its dimensions. Using the ideal gas equation PV = nRT, we can derive the dimensional expression for R.
From the equation PV = nRT, we know that:
R = PV/nT
Taking into account the dimensions of pressure, volume, number of moles, and temperature, we can express the dimensions of R as:
R = (force/area) x (volume/(amount x temperature))
Since area and volume can be expressed in terms of length, we have:
R = (force/length²) x (length^3/(amount x temperature))
Simplifying further, we find:
R = (force x length) / (amount x temperature)
Since force times length is equal to work, we can rewrite the equation as:
R = work / (amount x temperature)
Thus, the gas constant can be interpreted as work per degree per mole.
Relationship with the Boltzmann constant
The gas constant (R) is equivalent to the Boltzmann constant (k), but expressed in different units. The Boltzmann constant relates the energy scale in physics to the temperature scale for a single particle, while the gas constant relates the energy scale to the temperature scale for a mole of particles.
The relationship between R and k can be expressed as:
R = NA x k
Where NA is Avogadro’s constant.
By combining the Boltzmann constant and Avogadro’s constant, we can derive the value of the gas constant. Since the redefinition of SI base units in 2019, both Avogadro’s constant and the Boltzmann constant have exact numerical values when expressed in SI units. As a consequence, the SI value of the molar gas constant is exactly 8.31446261815324 J·K⁻¹·mol−1.
Measurement and Replacement with Defined Value
The most precise measurement of the gas constant has been obtained through experiments involving the speed of sound in argon at the temperature of the triple point of water. By extrapolating the speed of sound to the zero-pressure limit, the value of R can be determined.
However, since the redefinition of SI base units in 2019, the gas constant has an exact defined value. It is now defined in terms of other exactly defined physical constants, namely Avogadro’s constant and the Boltzmann constant.
This redefinition ensures that the value of the gas constant is fixed and does not rely on experimental measurements. The defined value of the gas constant in SI units is exactly 8.31446261815324 J·K⁻¹·mol−1.
:max_bytes(150000):strip_icc()/521928855-56a132c45f9b58b7d0bcf732.jpg)
Why R Is Used for the Gas Constant?
The symbol R is commonly used to represent the gas constant, but its origin is unclear. Some have suggested that it might be appropriate to name the symbol R the Regnault constant in honor of the French chemist Henri Victor Regnault, whose accurate experimental data were used to calculate the early value of the constant.
However, it is known that the gas constant was introduced independently by A.F. Horstmann, a student of Rudolf Clausius, and Dmitri Mendeleev. Mendeleev, known for his extensive measurements of the properties of gases, calculated the gas constant with high precision, within 0.3% of its modern value.
The choice of the symbol R for the gas constant is likely based on historical convention and practicality, as it has become widely recognized and accepted in scientific literature.
R in the U.S. Standard Atmosphere
In the U.S. Standard Atmosphere, the gas constant for atmospheric conditions is given as R = 8.31432 joules mol−1·K⁻¹. This value is specific to the U.S. Standard Atmosphere and is used in various applications by organizations such as NASA, NOAA, and the USAF.
The gas constant in the U.S. Standard Atmosphere is an essential parameter for atmospheric modeling and calculations related to air pressure, temperature, and density at different altitudes.
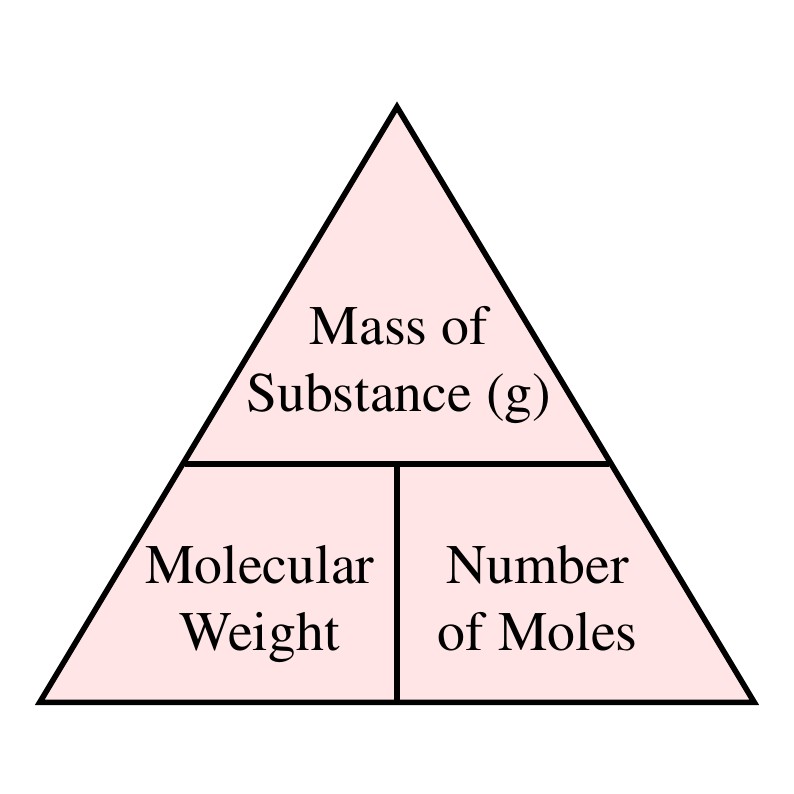
Mol and Molecular Weight
When working with gases, the concepts of moles and molecular weight are important. A mole (mol) is a unit of measurement used to express the amount of a substance. It is defined as the amount of a substance that contains the same number of particles as there are atoms in 12 grams of carbon-12.
The molecular weight of a substance is the sum of the atomic weights of all the atoms in a molecule. It is expressed in atomic mass units (amu) or grams per mole (g/mol). The molecular weight is an important factor when calculating the specific gas constant (Rspecific), which is the ratio of the molar gas constant (R) to the molecular weight (M) of a gas or gas mixture.
Universal Gas Constant and Ideal Gas Law
The universal gas constant (R) is a fundamental component of the ideal gas law. The ideal gas law is a combination of Boyle’s law, Charles’s law, and Avogadro’s law. It describes the behavior of an ideal gas, which is a theoretical gas that follows these three fundamental laws.
The ideal gas law can be expressed as PV = nRT, where P is the pressure, V is the volume, n is the number of moles, T is the temperature, and R is the gas constant. It implies the relation between these four variables and describes the state of any gas.
The ideal gas law is widely used in various applications, such as calculating the pressure, volume, or temperature of a gas under different conditions. It provides a simple and convenient way to analyze and understand the behavior of gases.
Boyle’s Law
Boyle’s law states that the pressure of a gas is inversely proportional to its volume when the temperature and amount of gas are held constant. Mathematically, it can be expressed as P ∝ 1/V.
This law was formulated by Robert Boyle in the 17th century based on his experiments with gases. He observed that as the volume of a gas decreased, the pressure exerted by the gas increased, and vice versa. Boyle’s law is one of the fundamental gas laws and is directly related to the gas constant (R) in the ideal gas law.

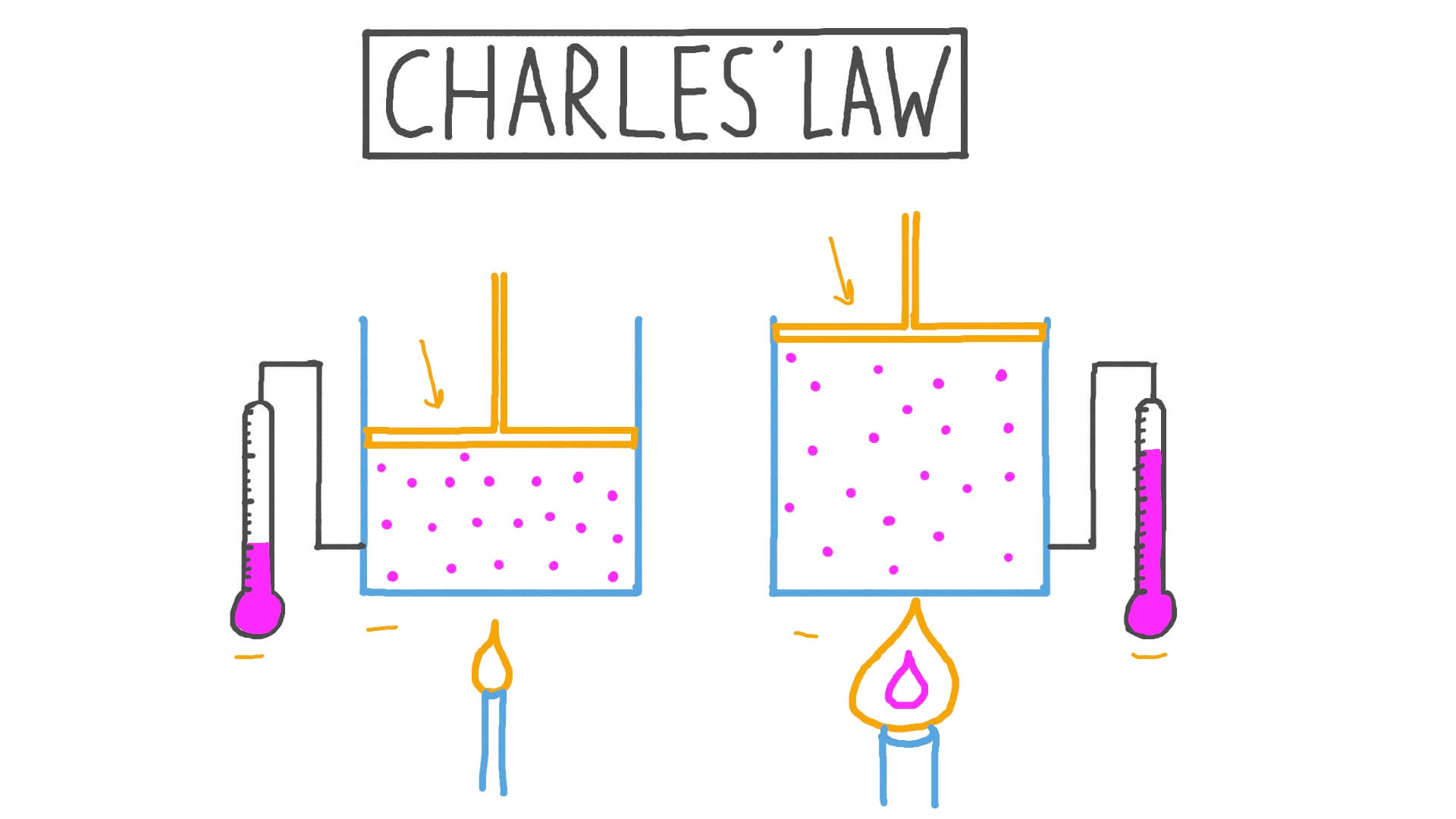
Charles Law
Charles’s law, also known as the law of volumes, states that the volume of a gas is directly proportional to its temperature when the pressure and amount of gas are held constant. Mathematically, it can be expressed as V ∝ T.
This law was formulated by Jacques Charles in the late 18th century based on his experiments with gases. He observed that as the temperature of a gas increased, the volume of the gas also increased, and vice versa. Charles’s law is another fundamental gas law and is related to the gas constant (R) in the ideal gas law.
Avogadro’s Law
Avogadro’s law states that equal volumes of gases, at the same temperature and pressure, contain an equal number of molecules. In other words, the volume of a gas is directly proportional to the amount of gas, expressed in moles, when the temperature and pressure are constant. Mathematically, it can be expressed as V ∝ n.
This law was formulated by Amedeo Avogadro in the early 19th century based on his hypothesis that equal volumes of gases, under the same conditions, contain an equal number of particles. Avogadro’s law is an essential component of the ideal gas law and is related to the gas constant (R).
:max_bytes(150000):strip_icc()/GettyImages-1632370171-5681b2ba5f9b586a9eec01d0.jpg)
Gay Lussac’s Law
Gay-Lussac’s law, also known as the pressure law, states that the pressure of a gas is directly proportional to its absolute temperature when the volume and amount of gas are held constant. Mathematically, it can be expressed as P ∝ T.
This law was formulated by Joseph Louis Gay-Lussac in the early 19th century based on his experiments with gases. He observed that as the temperature of a gas increased, the pressure exerted by the gas also increased, and vice versa. Gay-Lussac’s law is another fundamental gas law and is related to the gas constant (R) in the ideal gas law.

Applications of the Ideal Gas Law
The ideal gas law is widely used in various applications and fields of study. Some of the key applications include:
- Thermodynamics: The ideal gas law is fundamental to the study of thermodynamics, as it provides a basis for understanding the behavior of gases under different conditions.
- Chemical Reactions: The ideal gas law is used to calculate the stoichiometry of chemical reactions involving gases. It allows scientists to determine the amount of reactants and products based on their volumes, pressures, and temperatures.
- Gas Behavior: The ideal gas law helps in understanding the behavior of gases in various systems, such as industrial processes, combustion reactions, and gas mixtures.
- Atmospheric Science: The ideal gas law is used in atmospheric science to study the behavior of gases in the Earth’s atmosphere. It helps in understanding phenomena such as air pressure, temperature variations, and gas composition.
- Gas Laws: The ideal gas law is a fundamental component of other gas laws, such as Boyle’s law, Charles’s law, Avogadro’s law, and Gay-Lussac’s law. These laws describe specific relationships between the properties of gases and are essential in various scientific disciplines.
The applications of the ideal gas law are vast and cover a wide range of scientific and engineering fields. Its versatility and simplicity make it a valuable tool in understanding and analyzing gas behavior.
Solved Examples On Ideal Gas Constant
Let’s solve a few examples involving the ideal gas constant to better understand its applications.
Example 1: A gas sample occupies a volume of 2.5 liters at a pressure of 3 atmospheres and a temperature of 300 Kelvin. Calculate the number of moles of gas present.
Solution: Using the ideal gas law equation PV = nRT, we can rearrange the equation to solve for the number of moles (n): n = PV/RT
Substituting the given values: n = (3 atm)(2.5 L) / (0.0821 L·atm·K⁻¹·mol^-1)(300 K) n = 0.309 mol
Therefore, the number of moles of gas present is 0.309 mol.
Example 2: A gas sample has a volume of 10 liters at a pressure of 2 atmospheres and a temperature of 400 Kelvin. Calculate the volume of the gas sample at a pressure of 4 atmospheres and the same temperature.
Solution: Using the ideal gas law equation PV = nRT, we can rearrange the equation to solve for the volume (V): V = nRT/P
Substituting the given values: V = (n)(0.0821 L·atm·K⁻¹·mol^-1)(400 K) / (2 atm) V = 16.42 L
Therefore, the volume of the gas sample at a pressure of 4 atm and the same temperature is 16.42 L.
These examples demonstrate how the ideal gas constant can be used to solve problems involving the behavior of gases under different conditions.
How Kunduz Can Help You Learn Ideal Gas Constants?
At Kunduz, we understand the importance of a strong foundation in mathematics and physics. Our team of experienced teachers and experts is dedicated to providing comprehensive and engaging learning materials to help students excel in their academic journey.
Our resources cover a wide range of topics, including the ideal gas constant and its applications. We provide step-by-step explanations, solved examples, and practice problems to ensure a thorough understanding of the concepts.
Whether you’re preparing for exams, looking to expand your knowledge, or seeking assistance with homework, Kunduz is here to support you. Our user-friendly platform allows you to access learning materials anytime, anywhere, making learning convenient and flexible.
Join Kunduz today and embark on a rewarding learning experience that will help you master the ideal gas constant and other important concepts in mathematics and physics.
Frequently Asked Questions (FAQs) on Ideal Gas Constant
Here are some frequently asked questions about the ideal gas constant:
What is the Formula to Calculate the Specific Gas Constant?
The specific gas constant is calculated by dividing the molar gas constant (R) by the molar mass (M) of the gas or mixture. The formula is Rspecific = R/M.
The Ideal Gas Constant is the Combination of Which Laws?
The ideal gas constant is the combination of Boyle’s law, Charles’s law, Avogadro’s law, and Gay-Lussac’s law.
What is Avogadro’s Hypothesis?
Avogadro’s hypothesis states that equal volumes of gases, at the same temperature and pressure, contain the same number of molecules. This hypothesis laid the foundation for Avogadro’s law.
Why is R Used to Denote Gas Constants?
The choice of the symbol R to represent the gas constant is based on historical convention and practicality. It has become widely recognized and accepted in scientific literature, although its true origin is unclear.
These answers provide a better understanding of the ideal gas constant and its applications. If you have any further questions, feel free to explore our resources or consult with our experts.
In conclusion, the ideal gas constant plays a crucial role in the study of gases and their behavior under different conditions. Its value is fixed and depends on the units used for pressure, volume, and temperature. The gas constant is used in various applications, such as thermodynamics, chemical reactions, and atmospheric science. Understanding the gas constant and its applications is essential for a comprehensive understanding of gases and their properties.
