Polynomial functions are a fundamental concept in mathematics and have extensive applications in various fields. In this comprehensive guide, we will explore the definition of polynomial functions, their types, graphing techniques, polynomial equations, and provide solved examples to help you understand and master this topic.
An Introduction to Polynomial Functions
Polynomial functions are algebraic expressions that consist of variables, coefficients, and exponents. These functions are formed by combining terms, each of which has a variable raised to a non-negative integer exponent. The terms are then added or subtracted to create the polynomial function.
What is a Polynomial?
A polynomial is a mathematical expression that contains variables, coefficients, and exponents. The word “polynomial” is derived from the Latin words “poly” meaning “many” and “nomial” meaning “term.” Therefore, polynomials can be described as algebraic expressions with many terms.
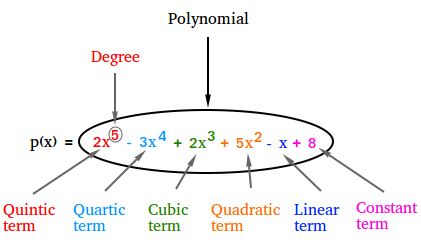
What is a Polynomial Function?
A polynomial function is a function that can be expressed as a polynomial. It is essentially a rule or equation that relates the input variable (usually denoted as x) to the output variable (usually denoted as y). Polynomial functions are widely used in various fields, including physics, engineering, economics, and computer science.
Graphs of Polynomial Functions
Graphing polynomial functions is an essential skill in understanding their behavior and characteristics. The graph of a polynomial function represents the relationship between the input variable (x) and the output variable (y). The shape and features of the graph provide valuable information about the polynomial function.
Graph for Constant Polynomial Function
A constant polynomial function is a polynomial with a degree of 0. It has the form f(x) = c, where c is a constant. The graph of a constant polynomial function is a horizontal line parallel to the x-axis.
Graph for Linear Polynomial Function
A linear polynomial function is a polynomial with a degree of 1. It has the form f(x) = mx + b, where m and b are constants. The graph of a linear polynomial function is a straight line with a constant slope.
Graph for Quadratic Polynomial Function
A quadratic polynomial function is a polynomial with a degree of 2. It has the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic polynomial function is a parabola, which can open upwards or downwards depending on the leading coefficient (a).
Graph for Higher Polynomial Function
Polynomial functions with degrees higher than 2 exhibit more complex graph shapes and features. They can have multiple turning points, or peaks and valleys, depending on the number and arrangement of their roots. The graph of a higher polynomial function may have multiple curves and branches.
Polynomial Equations
Polynomial equations are equations that involve polynomial expressions. These equations are solved by finding the values of the variables that make the equation true. The solutions to polynomial equations are called roots or zeros of the polynomial function.
Types of Polynomial Functions
Polynomial functions can be classified based on their degrees and the number of terms they contain. The most common types of polynomial functions are constant, linear, quadratic, cubic, and quartic functions.
Constant Polynomial Function
A constant polynomial function is a polynomial with a degree of 0. It has the form f(x) = c, where c is a constant. The graph of a constant polynomial function is a horizontal line parallel to the x-axis.
Zero Polynomial Function
A zero polynomial function is a polynomial with no terms other than the constant term 0. It has the form f(x) = 0. The graph of a zero polynomial function is a horizontal line at y = 0.
Linear Polynomial Function
A linear polynomial function is a polynomial with a degree of 1. It has the form f(x) = mx + b, where m and b are constants. The graph of a linear polynomial function is a straight line with a constant slope.
Quadratic Polynomial Function
A quadratic polynomial function is a polynomial with a degree of 2. It has the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic polynomial function is a parabola.
Cubic Polynomial Function
A cubic polynomial function is a polynomial with a degree of 3. It has the form f(x) = ax^3 + bx^2 + cx + d, where a, b, c, and d are constants. The graph of a cubic polynomial function can have up to two turning points.
Quartic Polynomial Function
A quartic polynomial function is a polynomial with a degree of 4. It has the form f(x) = ax^4 + bx^3 + cx^2 + dx + e, where a, b, c, d, and e are constants. The graph of a quartic polynomial function can have up to three turning points.
Degree of a Polynomial Function
The degree of a polynomial function is determined by the highest power of the variable in the polynomial expression. For example, in the polynomial function f(x) = 3x^2 + 2x + 1, the highest power of x is 2, so the degree of the polynomial function is 2.
The degree of a polynomial function provides important information about its behavior and characteristics. It determines the number of turning points the graph may have and helps in analyzing the end behavior of the function.
Standard Form of Different Types of Polynomial Function
Polynomial functions can be written in standard form, which is a specific representation of the polynomial expression. The standard form of a polynomial function is written as f(x) = anxn + an-1xn-1 + … + a2x^2 + a1x + a0, where an, an-1, …, a2, a1, and a0 are constants.
The standard form of a polynomial function helps in identifying the leading coefficient (an), which is the coefficient of the term with the highest power of the variable. The leading coefficient plays a significant role in determining the end behavior of the function.
General Form of Different Types of Polynomial Function
Polynomial functions can also be written in general form, which is a more expanded representation of the polynomial expression. The general form of a polynomial function is written as f(x) = axn + bxn-1 + … + cx^2 + dx + e, where a, b, c, d, and e are constants.
The general form of a polynomial function provides a more detailed view of the coefficients and variables involved in the expression. It allows for a more comprehensive analysis of the polynomial function’s behavior and characteristics.
How to Determine a Polynomial Function?
To determine a polynomial function, several conditions need to be met regarding the exponents of the variables:
- The exponent of the variable in every term must be a non-negative whole number. It cannot be a fraction or a negative number.
- The variable should not be inside a radical, such as a square root or a cube root.
- The variable should not be in the denominator of any term.
By checking these conditions, we can determine if a given function is a polynomial function or not.
Turning Points of Polynomial Functions
Turning points, also known as local extrema, are the points on the graph of a polynomial function where the function changes direction. These points occur at the peaks or valleys of the graph and can be found by analyzing the derivative of the function.
The number of turning points a polynomial function can have is determined by its degree. A polynomial function of degree n can have at most n-1 turning points.
Roots of Polynomial Functions
The roots of a polynomial function are the values of the variable that make the function equal to zero. These values are also known as zeros or x-intercepts of the function and can be found by solving the polynomial equation f(x) = 0.
The number of roots a polynomial function can have is equal to its degree. For example, a quadratic polynomial function of degree 2 can have up to two distinct roots.
Solved Examples on Polynomial Functions
Let’s solve a few examples to illustrate the concepts of polynomial functions.
Example 1: Consider the polynomial function f(x) = 3x^2 – 5x + 2. Determine the degree of the polynomial and find its roots.
Solution: The degree of the polynomial function is determined by the highest power of the variable, which is 2 in this case. Therefore, the polynomial function has a degree of 2.
To find the roots, we set the function equal to zero: 3x^2 – 5x + 2 = 0
We can factorize the quadratic expression: (3x – 2)(x – 1) = 0
Setting each factor equal to zero gives us the roots: 3x – 2 = 0 –> x = 2/3 x – 1 = 0 –> x = 1
Therefore, the roots of the polynomial function are x = 2/3 and x = 1.
Example 2: Graph the polynomial function f(x) = x^3 – 4x^2 + 3x + 2.
Solution: To graph the polynomial function, we can first determine the behavior at the x-intercepts and turning points. By solving the equation f(x) = 0, we find the x-intercepts to be x = -2, x = 1, and x = 2.
To find the turning points, we can analyze the derivative of the function. Taking the derivative of f(x), we get f'(x) = 3x^2 – 8x + 3. Setting f'(x) equal to zero and solving, we find the x-coordinate of the turning point to be x = 1/3.
Using this information, we can plot the x-intercepts (-2, 0), (1, 0), and (2, 0), as well as the turning point (1/3, f(1/3)).
By connecting these points, we can sketch the graph of the polynomial function.
How Kunduz Can Help You Learn Polynomial Functions?
At Kunduz, we understand the importance of mastering polynomial functions in your academic journey. That’s why we offer comprehensive resources and personalized tutoring to help you learn and excel in this topic.
Our expert tutors are experienced in teaching polynomial functions and can provide step-by-step guidance tailored to your learning needs. Whether you need help understanding the basics, solving complex equations, or graphing polynomial functions, our tutors are here to assist you.
With Kunduz, learning polynomial functions becomes an enjoyable and rewarding experience. Our affordable and accessible learning platform ensures that you have the support you need, whenever you need it.
Don’t let polynomial functions intimidate you. Join Kunduz today and embark on a journey of mathematical excellence!
