In the realm of mathematics, polynomials play a vital role. They are widely used in various fields such as physics, engineering, computer science, and economics. Understanding the concept of polynomials is crucial for mastering these subjects. In this article, we will delve into the definition, types, functions, degree, operations, and solved examples of polynomials.
What is Polynomial?
A polynomial is a mathematical expression that consists of variables, coefficients, and operations like addition, subtraction, and multiplication. The variables are raised to non-negative integer exponents, and each term is a product of a coefficient and a variable raised to a specific exponent.
For example, consider the polynomial 3x^2 + 2x + 1. In this expression, 3, 2, and 1 are coefficients, x is the variable, and 2, 1, and 0 are the exponents. The terms in this polynomial are 3x^2, 2x, and 1.
Polynomials can have multiple terms and can involve more than one variable.
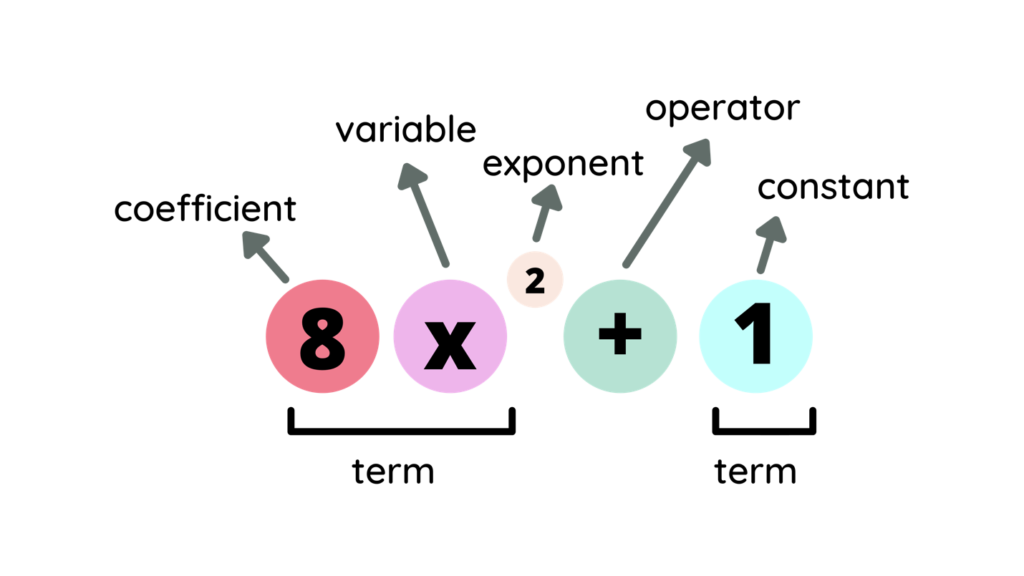
Standard Form of a Polynomial
Polynomials are often written in standard form, which means that the terms are arranged in descending order of their exponents. The standard form of a polynomial is determined by the degree of the polynomial, which is the highest exponent in the polynomial.
For example, let’s rewrite the polynomial 3x^2 + 2x + 1 in standard form. Since the highest exponent is 2, the polynomial can be written as 3x^2 + 2x + 1.
Polynomial Equations
Polynomials can also be used to represent equations. A polynomial equation is an equation in which a polynomial expression is set equal to zero. The solutions to the equation are the values of the variable(s) that make the polynomial equal to zero.
For example, consider the polynomial equation x^2 + 4x – 5 = 0. The solutions to this equation are the values of x that satisfy the equation, which in this case are x = 1 and x = -5.
Types of Polynomials
There are different types of polynomials based on the number of terms they contain. Let’s explore the different types of polynomials:
Monomial
A monomial is a polynomial with only one term. The term can consist of a variable raised to a non-negative integer exponent multiplied by a coefficient.
Examples of monomials include 3x, 5xy^2, and -7.
Binomial
A binomial is a polynomial with two terms. The terms can be added or subtracted from each other.
Examples of binomials include 2x + 3, x^2 – 4, and 5xy + 2.
Trinomial
A trinomial is a polynomial with three terms. The terms can be added or subtracted from each other.
Examples of trinomials include x^2 + 3x + 2, 2xy^2 – 5y + 7, and 3x^3 – 4x^2 + x.
Quadrinomial
A quadrinomial is a polynomial with four terms. The terms can be added or subtracted from each other.
Examples of quadrinomials include 2x^3 + 3x^2 – 4x + 5, 5xy^2 – 3y + 2x^2, and 4x^4 + 2x^3 – 3x^2 + x.
Polynomials can have more than four terms, and they can be classified based on their degree as well.
Operations on Polynomials
There are several operations that can be performed on polynomials, including addition, subtraction, multiplication, and division. Let’s explore each operation in detail:
Addition of Polynomials
When adding polynomials, it is important to combine the like terms. Like terms are the terms that have the same variable and exponent. To add polynomials, simply add the coefficients of the like terms while keeping the variables and exponents the same.
For example, let’s add the polynomials 3x^2 + 2x + 1 and 2x^2 + 4x + 3. To add these polynomials, we add the like terms: (3x^2 + 2x^2) + (2x + 4x) + (1 + 3) = 5x^2 + 6x + 4.
Subtraction of Polynomials
Subtracting polynomials is similar to adding them. Again, it is important to combine the like terms. To subtract polynomials, subtract the coefficients of the like terms while keeping the variables and exponents the same.
For example, let’s subtract the polynomial 3x^2 + 2x + 1 from the polynomial 5x^2 + 4x + 3. To subtract these polynomials, we subtract the like terms: (5x^2 – 3x^2) + (4x – 2x) + (3 – 1) = 2x^2 + 2x + 2.
Multiplication of Polynomials
To multiply polynomials, we use the distributive property. Multiply each term of one polynomial by each term of the other polynomial, and then combine like terms.
For example, let’s multiply the polynomials (x + 2) and (x – 3). To multiply these polynomials, we use the distributive property: (x + 2)(x – 3) = x(x – 3) + 2(x – 3) = x^2 – 3x + 2x – 6 = x^2 – x – 6.
Division of Polynomials
Division of polynomials involves dividing one polynomial by another polynomial. The result is a quotient polynomial and a remainder polynomial.
For example, let’s divide the polynomial 3x^2 + 2x + 1 by the polynomial x + 1. To divide these polynomials, we can use long division or synthetic division. The quotient polynomial is 3x + 1, and the remainder is 0.
Factorization of Polynomials
Factorization of polynomials involves expressing a polynomial as a product of its factors. Factors are polynomials that can be multiplied together to obtain the original polynomial.
To factorize a polynomial, we look for common factors, factor out the greatest common factor, and then use techniques like factoring by grouping, factoring trinomials, and factoring special products.
For example, let’s factorize the polynomial x^2 + 2x + 1. In this case, the polynomial is a perfect square trinomial, and it can be factored as (x + 1)(x + 1) or (x + 1)^2.
How To Factor Polynomials?
Factoring polynomials can sometimes be challenging, but there are several strategies and techniques that can help make the process easier. Let’s go through a step-by-step guide on how to factor polynomials:
Step 1: Look for the greatest common factor (GCF) of the coefficients and variables in the polynomial. The GCF is the largest number or term that can be divided evenly into all the terms of the polynomial.
Step 2: Factor out the GCF from the polynomial by dividing each term by the GCF. This step simplifies the polynomial and makes further factoring easier.
Step 3: Identify any special factoring patterns, such as perfect square trinomials or the difference of squares. These patterns can help simplify the polynomial further.
Step 4: Use factoring techniques like factoring by grouping or factoring quadratic trinomials to factorize the polynomial completely.
Step 5: Check your factoring by multiplying the factors back together. The result should be the original polynomial.
Characteristics of Polynomials
Polynomials have several characteristics that are important to understand. Let’s explore some of these characteristics:
- Degree: The degree of a polynomial is the highest exponent of the variable in the polynomial. It determines the overall behavior of the polynomial.
- Leading Coefficient: The leading coefficient is the coefficient of the term with the highest exponent. It affects the shape and direction of the polynomial’s graph.
- Zeros: Zeros of a polynomial are the values of the variable that make the polynomial equal to zero. They are also known as roots or solutions of the polynomial equation.
- Graph: The graph of a polynomial represents the relationship between the variable and the polynomial expression. It can provide insights into the behavior and characteristics of the polynomial.
Polynomial Functions
Polynomials can be used to represent functions. A polynomial function is a function that is defined by a polynomial expression. The input to the function is the variable, and the output is the result of evaluating the polynomial expression.
For example, consider the polynomial function f(x) = x^2 + 2x + 1. When we substitute different values of x into the function, we get the corresponding outputs. The graph of the function represents the relationship between the input and output values.
Degree of a Polynomial
The degree of a polynomial is the highest exponent of the variable in the polynomial expression. It determines the overall behavior and complexity of the polynomial. The degree can be used to classify polynomials into different categories.
For example, the polynomial 3x^2 + 2x + 1 has a degree of 2 because the highest exponent is 2. Similarly, the polynomial 5x^3 – 2x^2 + 4x has a degree of 3 because the highest exponent is 3.
The degree of a polynomial can help us understand its properties and characteristics, such as the number of zeros and the shape of the graph.
Terms of a Polynomial
A polynomial is composed of multiple terms, each separated by addition or subtraction operators. Each term consists of a coefficient multiplied by a variable raised to a specific exponent.
For example, in the polynomial 3x^2 + 2x + 1, there are three terms: 3x^2, 2x, and 1. The term 3x^2 has a coefficient of 3 and an exponent of 2. The term 2x has a coefficient of 2 and an exponent of 1. The term 1 is a constant term with no variables.
Understanding the terms of a polynomial is important for performing operations on polynomials, such as addition, subtraction, and multiplication.
Properties of Polynomials
Polynomials have several properties that can be useful in solving equations and understanding their behavior. Let’s explore some of these properties:
- Division Algorithm: The division algorithm states that for any two polynomials P(x) and Q(x), where Q(x) is not equal to zero, there exist unique polynomials Q'(x) and R(x) such that P(x) = Q(x)Q'(x) + R(x), where the degree of R(x) is less than the degree of Q(x).
- Bezout’s Theorem: Bezout’s theorem states that if a polynomial P(x) is divided by the polynomial x – a, then P(a) = 0 is always true. This theorem helps us find the zeros of a polynomial.
- Remainder Theorem: The remainder theorem states that if a polynomial P(x) is divided by the polynomial x – a, then the remainder is equal to P(a).
- Factor Theorem: The factor theorem states that if a polynomial P(x) is divided by the polynomial x – a, and the remainder is zero, then x – a is a factor of P(x).
- Intermediate Value Theorem: The intermediate value theorem states that if a polynomial P(x) is continuous on an interval [a, b], and P(a) and P(b) have opposite signs, then there exists at least one value c in the interval [a, b] such that P(c) = 0.
- Descartes’ Rule of Sign: Descartes’ rule of sign helps us determine the possible number of positive and negative zeros of a polynomial.
- Fundamental Theorem of Algebra: The fundamental theorem of algebra states that every polynomial equation of degree n, where n is a positive integer, has exactly n complex roots.
Understanding these properties can help us solve polynomial equations, find zeros, and analyze the behavior of polynomials.
Solving Polynomials
Solving polynomials involves finding the values of the variable(s) that make the polynomial equal to zero. These values are called zeros or roots of the polynomial. Solving polynomials can be done using different methods, depending on the degree of the polynomial.
Zeros of Polynomials
The zeros of a polynomial are the values of the variable(s) that make the polynomial equal to zero. To find the zeros of a polynomial, we set the polynomial equal to zero and solve for the variable(s).
For example, let’s find the zeros of the polynomial x^2 – 4x + 3. To find the zeros, we set the polynomial equal to zero: x^2 – 4x + 3 = 0. We can then factorize the polynomial: (x – 3)(x – 1) = 0. Setting each factor equal to zero gives us the zeros: x – 3 = 0 and x – 1 = 0. Solving these equations, we find that the zeros are x = 3 and x = 1.
How to Find Zeros of Polynomials?
Finding the zeros of a polynomial can sometimes be challenging, especially for higher degree polynomials. Here are some steps to help you find the zeros of a polynomial:
Step 1: Factorize the polynomial as much as possible. Look for common factors and factor out the greatest common factor (GCF).
Step 2: Use factoring techniques like factoring by grouping, factoring trinomials, or factoring special products to further factorize the polynomial.
Step 3: Set each factor equal to zero and solve for the variable(s). These are the zeros of the polynomial.
Step 4: Check your solutions by substituting them back into the original polynomial equation. The result should be zero.
By following these steps, you can find the zeros of a polynomial and determine the values of the variable(s) that make the polynomial equal to zero.
Solving Linear Polynomials
Linear polynomials are polynomials of degree 1. Solving linear polynomials involves isolating the variable and solving for its value.
For example, let’s solve the linear polynomial 2x – 3 = 0. To solve this polynomial, we isolate the variable by adding 3 to both sides of the equation: 2x = 3. Then, we divide both sides by 2 to solve for x: x = 3/2 or x = 1.5.
Solving Quadratic Polynomials
Quadratic polynomials are polynomials of degree 2. Solving quadratic polynomials can be done using different methods, such as factoring, completing the square, or using the quadratic formula.
For example, let’s solve the quadratic polynomial x^2 – 4x + 3 = 0. We can factorize the polynomial as (x – 3)(x – 1) = 0. Setting each factor equal to zero gives us x – 3 = 0 and x – 1 = 0. Solving these equations, we find that the zeros are x = 3 and x = 1.
Polynomial Expressions
Polynomials can be used to represent various mathematical expressions. There are different types of polynomial expressions, including trigonometric polynomials, matrix polynomials, and exponential polynomials.
Trigonometric Polynomials
Trigonometric polynomials involve trigonometric functions like sine, cosine, and tangent. These polynomials can be used to model periodic functions and waveforms.
For example, the polynomial expression f(x) = 3sin(x) + 2cos(x) is a trigonometric polynomial. It represents a function that combines sine and cosine functions.
Matrix Polynomials
Matrix polynomials involve matrices and matrix operations. These polynomials are often used in linear algebra and can represent systems of linear equations.
For example, the polynomial expression A^2 – 3A + 2I, where A is a matrix and I is the identity matrix, is a matrix polynomial. It represents a polynomial expression involving matrix multiplication and addition.
Exponential Polynomials
Exponential polynomials involve exponential functions like e^x. These polynomials can model exponential growth or decay.
For example, the polynomial expression f(x) = 2e^x – 3e^-x is an exponential polynomial. It represents a function that combines exponential growth and decay.
Components of Polynomials
Polynomials have different components that can help us analyze and understand their properties. These components include the leading term, constant term, and coefficients.
- Leading Term: The leading term of a polynomial is the term with the highest degree or exponent. It determines the overall behavior and shape of the polynomial.
- Constant Term: The constant term of a polynomial is the term with no variables. It is a constant value that is added or subtracted from the other terms.
- Coefficients: The coefficients of a polynomial are the numbers that multiply the variables in each term. They determine the magnitude and direction of the polynomial.
- Leading Term: The leading term of a polynomial is the term with the highest degree or exponent. It determines the overall behavior and shape of the polynomial.
- Constant Term: The constant term of a polynomial is the term with no variables. It is a constant value that is added or subtracted from the other terms.
- Coefficients: The coefficients of a polynomial are the numbers that multiply the variables in each term. They determine the magnitude and direction of the polynomial.
Understanding the components of polynomials can help us analyze their properties, graph them, and solve equations involving them.
Higher Degree Polynomial
Higher degree polynomials are polynomials with degrees greater than 2. These polynomials can have more complex behavior and multiple zeros.
For example, a cubic polynomial is a polynomial of degree 3, and a quartic polynomial is a polynomial of degree 4. Higher degree polynomials can have multiple zeros, turning points, and complex graphs.
Understanding higher degree polynomials requires advanced techniques and methods, such as factoring, synthetic division, and the rational root theorem.
Solved Examples on Polynomials
Let’s solve some examples to further understand the concepts of polynomials:
Example: Solve the equation x^2 – 5x + 6 = 0.
To solve this equation, we can factorize the polynomial: (x – 2)(x – 3) = 0. Setting each factor equal to zero gives us x – 2 = 0 and x – 3 = 0. Solving these equations, we find that the zeros are x = 2 and x = 3.
How Kunduz Can Help You Learn Polynomials?
Understanding polynomials and their operations, degrees, types, and properties can be a daunting task. However, with the right resources and guidance, anyone can master this fundamental concept in algebra. Kunduz provides expert guidance to help students learn polynomials in an engaging and effective manner. With Kunduz, you can take your understanding of polynomials to the next level.
