Trigonometric functions are fundamental mathematical functions that establish relationships between the angles and sides of a right triangle. Often referred to as trig functions, they are widely used in various fields such as mathematics, physics, and engineering. Trigonometry itself is a branch of mathematics that deals with the study of triangles and the relationships between their angles and sides.
What is Trigonometry?
Trigonometry is a branch of mathematics that focuses on the relationships between angles and sides of triangles. It is derived from the Greek words “trigonon” meaning triangle and “metron” meaning measure. Trigonometry provides a framework for understanding and solving problems involving angles, distances, and heights.

What is a Trigonometric Function?
A trigonometric function is a mathematical function that relates the angles of a right triangle to the ratios of the lengths of its sides. The primary trigonometric functions are sine (sin), cosine (cos), and tangent (tan). These functions are defined based on the ratios of the sides of a right triangle and can be used to calculate unknown angles or side lengths.
Six Trigonometric Functions
There are six basic trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. Each function relates an angle to the ratio of two sides of a right triangle. Here is a brief explanation of each function:
Sine Function
The sine function (sin) is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. In other words, sin(theta) = opposite/hypotenuse.
Cosine Function
The cosine function (cos) is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. In other words, cos(theta) = adjacent/hypotenuse.
Tangent Function
The tangent function (tan) is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. In other words, tan(theta) = opposite/adjacent.
Cosecant Function
The cosecant function (cosec) is the reciprocal of the sine function. It is defined as the ratio of the length of the hypotenuse to the length of the side opposite the angle. In other words, cosec(theta) = 1/sin(theta).
Secant Function
The secant function (sec) is the reciprocal of the cosine function. It is defined as the ratio of the length of the hypotenuse to the length of the side adjacent to the angle. In other words, sec(theta) = 1/cos(theta).
Cotangent Function
The cotangent function (cot) is the reciprocal of the tangent function. It is defined as the ratio of the length of the side adjacent to the angle to the length of the side opposite the angle. In other words, cot(theta) = 1/tan(theta).
Trigonometric Formulas
Trigonometric functions can be represented using different formulas depending on the relationship between the angles and sides of a right triangle. These formulas help in solving trigonometric problems and finding the values of the trigonometric functions. Here are some of the key formulas:
- Sine Formula: sin(theta) = opposite/hypotenuse
- Cosine Formula: cos(theta) = adjacent/hypotenuse
- Tangent Formula: tan(theta) = opposite/adjacent
- Cosecant Formula: cosec(theta) = 1/sin(theta)
- Secant Formula: sec(theta) = 1/cos(theta)
- Cotangent Formula: cot(theta) = 1/tan(theta)
These formulas allow us to calculate the values of the trigonometric functions for any given angle in a right triangle.
Trigonometric Functions Identities
Trigonometric function identities are equations that relate the values of different trigonometric functions. These identities help simplify trigonometric expressions and solve trigonometric equations. Here are some important trigonometric identities:
Reciprocal Identities
Reciprocal identities relate the reciprocal of one trigonometric function to another trigonometric function. They are as follows:
- cosec(theta) = 1/sin(theta)
- sec(theta) = 1/cos(theta)
- cot(theta) = 1/tan(theta)
- sin(theta) = 1/cosec(theta)
- cos(theta) = 1/sec(theta)
- tan(theta) = 1/cot(theta)
Pythagorean Identities
Pythagorean identities are equations derived from the Pythagorean theorem and relate the values of the trigonometric functions. They are as follows:
- sin^2(theta) + cos^2(theta) = 1
- 1 + tan^2(theta) = sec^2(theta)
- 1 + cot^2(theta) = cosec^2(theta)
Sum and Difference Identities
Sum and difference identities are equations that relate the trigonometric functions of the sum or difference of two angles to the trigonometric functions of the individual angles. They are as follows:
- sin(A + B) = sin(A)cos(B) + cos(A)sin(B)
- cos(A + B) = cos(A)cos(B) – sin(A)sin(B)
- tan(A + B) = (tan(A) + tan(B))/(1 – tan(A)tan(B))
- sin(A – B) = sin(A)cos(B) – cos(A)sin(B)
- cos(A – B) = cos(A)cos(B) + sin(A)sin(B)
- tan(A – B) = (tan(A) – tan(B))/(1 + tan(A)tan(B))
Half-Angle Identities
Half-angle identities are equations that relate the trigonometric functions of half of an angle to the trigonometric functions of the full angle. They are as follows:
- sin(A/2) = ±√[(1 – cos(A))/2]
- cos(A/2) = ±√[(1 + cos(A))/2]
- tan(A/2) = ±√[(1 – cos(A))/(1 + cos(A))]
Double Angle Identities
Double angle identities are equations that relate the trigonometric functions of twice an angle to the trigonometric functions of the original angle. They are as follows:
- sin(2A) = 2sin(A)cos(A)
- cos(2A) = cos^2(A) – sin^2(A)
- tan(2A) = (2tan(A))/(1 – tan^2(A))
Domain and Range of Trigonometric Functions
The domain of a trigonometric function is the set of all possible input values (angles) for which the function is defined. The range of a trigonometric function is the set of all possible output values (ratios) that the function can take. Here is a table showing the domain and range of the six trigonometric functions:
| Trigonometric Function | Domain | Range |
|---|---|---|
| sin(theta) | R | [-1, 1] |
| cos(theta) | R | [-1, 1] |
| tan(theta) | R – (2n + 1)π/2 | R |
| cosec(theta) | R – nπ | (-∞, -1] U [1, ∞) |
| sec(theta) | R – (2n + 1)π/2 | (-∞, -1] U [1, ∞) |
| cot(theta) | R – nπ | R – nπ |
These values represent the valid input angles and the corresponding output ratios for each trigonometric function.
Inverse Trigonometric Functions
Inverse trigonometric functions are the opposite of trigonometric functions. They allow us to find the angle (input) given the ratio (output) of a trigonometric function. Inverse trigonometric functions are denoted by adding “arc” or “a” before the trigonometric function. For example, the inverse of the sine function is denoted as arcsin or asin. Here are the inverse trigonometric functions:
- arcsin(x) or asin(x): the inverse of sin(x)
- arccos(x) or acos(x): the inverse of cos(x)
- arctan(x) or atan(x): the inverse of tan(x)
- arccosec(x) or acosec(x): the inverse of cosec(x)
- arcsec(x) or asec(x): the inverse of sec(x)
- arccot(x) or acot(x): the inverse of cot(x)
The range of inverse trigonometric functions is limited to certain angles, depending on the function. For example, the range of arcsin(x) is -π/2 to π/2, and the range of arccos(x) is 0 to π.
Trigonometric Functions Derivatives
The derivative of a function measures the rate of change of the function with respect to its independent variable. The derivatives of trigonometric functions are useful in calculus and are derived using the basic trigonometric identities. Here are the derivatives of the six trigonometric functions:
- d/dx (sin(x)) = cos(x)
- d/dx (cos(x)) = -sin(x)
- d/dx (tan(x)) = sec^2(x)
- d/dx (cot(x)) = -cosec^2(x)
- d/dx (sec(x)) = sec(x)tan(x)
- d/dx (cosec(x)) = -cosec(x)cot(x)
These derivatives can be used to find the rate of change of trigonometric functions and solve calculus problems involving trigonometric functions.
Integration of Trigonometric Functions
Integration is the reverse process of differentiation and allows us to find the area under a curve. The integration of trigonometric functions is useful in calculus and can be used to solve various mathematical problems. Here are the integrals of the six trigonometric functions:
- ∫ sin(x) dx = -cos(x) + C
- ∫ cos(x) dx = sin(x) + C
- ∫ tan(x) dx = -ln|cos(x)| + C
- ∫ cot(x) dx = ln|sin(x)| + C
- ∫ sec(x) dx = ln|sec(x) + tan(x)| + C
- ∫ cosec(x) dx = ln|cosec(x) – cot(x)| + C
These integrals can be used to find the area under a curve defined by a trigonometric function and solve integration problems involving trigonometric functions.
Graphs of Trigonometric Functions
The graphs of trigonometric functions show the relationship between the angle (input) and the ratio (output) of the trigonometric function. The graphs of trigonometric functions have specific patterns and shapes that repeat periodically. The sine and cosine functions, for example, produce wave-like patterns, while the tangent function has vertical asymptotes. The graphs of trigonometric functions can be used to analyze and interpret various real-life phenomena, such as the motion of pendulums and the behavior of waves.
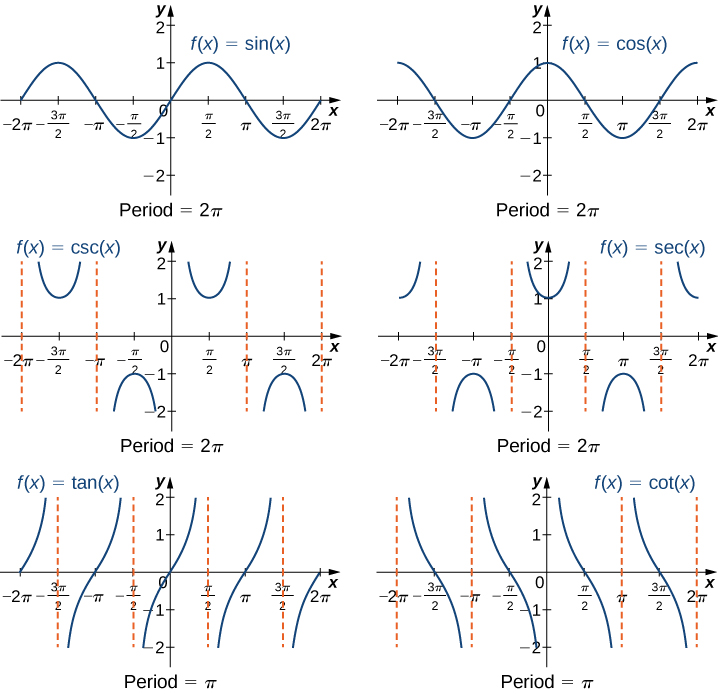
Trigonometric Functions Values
The values of trigonometric functions can be evaluated for specific angles using reference angles and the unit circle. The values of sine, cosine, and tangent for various angles are commonly used and can be found in trigonometric tables or calculated using trigonometric functions calculators. Here are some key values for the trigonometric functions:
| Angle (degrees) | sin(theta) | cos(theta) | tan(theta) | cosec(theta) | sec(theta) | cot(theta) |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | undefined | 1 | undefined |
| 30 | 1/2 | √3/2 | √3/3 | 2 | 2√3/3 | √3 |
| 45 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60 | √3/2 | 1/2 | √3 | 2/√3 | 2 | 1/√3 |
| 90 | 1 | 0 | undefined | 1 | undefined | 0 |
These values can be used to solve trigonometric problems and find the exact values of trigonometric functions for specific angles.
Trigonometric Functions Table
A trigonometric functions table provides a comprehensive list of values for the trigonometric functions at various angles. These tables are useful for quick reference and can be used to find the values of trigonometric functions for specific angles without calculations. Here is an example table showing the values of the trigonometric functions for selected angles:
| Function | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin(x) | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos(x) | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tan(x) | 0 | √3/3 | 1 | √3 | – |
| cosec(x) | – | 2 | √2 | 2/√3 | – |
| sec(x) | 1 | 2/√3 | √2 | 2 | – |
| cot(x) | – | √3 | 1 | 1/√3 | – |
This table can be used to quickly find the values of the trigonometric functions for the given angles.
Explanation of Trigonometric Functions in Four Quadrants
Trigonometric functions can be positive or negative depending on the quadrant in which the angle lies. The four quadrants divide the coordinate plane into different regions, and the signs of the trigonometric functions vary accordingly. Here is an explanation of the trigonometric functions in the four quadrants:
- In the first quadrant (0° to 90°), all trigonometric functions are positive.
- In the second quadrant (90° to 180°), only the sine and cosecant functions are positive.
- In the third quadrant (180° to 270°), only the tangent and cotangent functions are positive.
- In the fourth quadrant (270° to 360°), only the cosine and secant functions are positive.
These relationships help determine the signs of the trigonometric functions for any given angle.
Differentiation of Trigonometric Functions
The differentiation of trigonometric functions involves finding the derivatives of the trigonometric functions with respect to the independent variable (usually x). The derivatives of the six trigonometric functions can be found using the chain rule and the basic trigonometric identities. Here are the derivatives of the trigonometric functions:
- d/dx (sin(x)) = cos(x)
- d/dx (cos(x)) = -sin(x)
- d/dx (tan(x)) = sec^2(x)
- d/dx (cot(x)) = -cosec^2(x)
- d/dx (sec(x)) = sec(x)tan(x)
- d/dx (cosec(x)) = -cosec(x)cot(x)
These derivatives are useful in calculus and can be used to find the rate of change of trigonometric functions and solve various mathematical problems.
Solved Examples on Trigonometric Functions
To better understand how to apply trigonometric functions, let’s solve a few examples:
Example 1: Find the value of sin(45°).
Solution: From the trigonometric functions table, we can see that sin(45°) = √2/2.
Example 2: Evaluate cos(60°).
Solution: From the trigonometric functions table, we can see that cos(60°) = 1/2.
Example 3: Calculate the value of tan(30°).
Solution: From the trigonometric functions table, we can see that tan(30°) = √3/3.
These examples demonstrate how to find the values of trigonometric functions for specific angles using the trigonometric functions table.
How Kunduz Can Help You Learn Trigonometric Functions?
Kunduz is an online learning platform that offers comprehensive resources and tools to help students learn and understand trigonometric functions. With Kunduz, you can access interactive lessons, practice exercises, and step-by-step tutorials that break down complex concepts into easily understandable chunks. Whether you’re a beginner or an advanced learner, Kunduz provides a personalized learning experience tailored to your needs. With our intuitive interface and engaging content, you can master trigonometric functions and excel in your mathematics studies.
