Türev Nedir?
Türev, diğer sayı kümeleri üzerindeki fonksiyonlar için de genellenmiş olmasına rağmen öncelikle reel değerli, yani reel sayılardan reel sayılara giden tek değişkenli fonksiyonlar için tanımlanmış, herhangi bir teğetin herhangi bir eğriye x ekseniyle yaptığı pozitif yönlü açının tanjant değeridir.
Türevin kelime anlamı Türk Dil Kurumu’na göre “türemiş veya üretilmiş şey” demektir. Matematikteki türev ise “değişken artması sıfıra giderken, fonksiyonun artmasının değişken artmasına oranı limiti” olarak tanımlanır.
Türev, bir miktarın diğerine göre değişim oranını hesaplamaya yarar. Bu miktarları matematik dersinde fonksiyonlar başlığı altında soyut olarak görsek de, fonksiyonların gerçek hayatta da olduğunu hatırlamak türevin somut örneklerde anlaşılması için yararlı olabilir.
Türev mühendislik, ekonomi, fizik, biyoloji, kimya gibi birçok alanda kullanılır.
Türev Alma Kuralları
Sabit Fonksiyonun Türevi
Sabit fonksiyonların türevi 0’dır. Yani; f(x)=c ve c ϵ R için f'(x) = 0 olur.
Örnek: f(x) = 12 olsun. Bu durumda sabit fonksiyon olduğu için her noktasındaki türevi 0’dır.
f'(x) = 0 yazılır.
Üslü Fonksiyonların Türevi
N ϵ R olmak üzere f(x) = x^n ise f'(x) = n. x^{n-1} yazılır. Yani üslü fonksiyonlarda türev alırken terimin kuvveti, terimin başına katsayı olarak gelir ve terimin kuvveti 1 azaltılır.
Örnek: f(x) = x^4 ise f'(x) = 4. x^{4-1} = 4.x^3 olur.
Eğer fonksiyonumuz katsayılı olarak verilirse de çözmek çok kolay. c ϵ R bir sabit sayı olmak üzere fonksiyon c.f(x) şeklinde verildiğinde fonksiyonun türevi c . f’(x) olur.
Örnek: f(x) = 7.x^3 ise f'(x) = 7.3. x^{3-1} = 21.x^2 olur.
İki Fonksiyonun Toplamının Türevi
İki fonksiyonun toplamının türevi [f(x) + g(x)]’ = f’(x) + g’(x) şeklindedir. f ve g fonksiyonları x noktasında türevli iki fonksiyon olmak üzere, f + g fonksiyonu da x noktasında türevlidir.
İki Fonksiyonun Çarpımının Türevi
f(x) ve g(x), x noktasında türevli iki fonksiyon olmak üzere; çarpım türevi
[f(x) . g(x)]’ = f’(x) . g(x) + f(x) . g’(x) şeklinde yazılır. Ve bu elde ettiğimiz çarpım fonksiyonu da x noktasında türevlidir denir.
Not: “birincinin türevi çarpı ikinci + ikincinin türevi çarpı ikinci” diyerek formülü daha kolay hatırlayabilirsin.

İki Fonksiyonun Bölümünün Türevi
f ve g, x noktasında türevli olan iki fonksiyon ve g(x) ≠ 0 olmak üzere,
f(x) / g(x) fonksiyonunun da bölmenin türevi x noktasında alınabilir. Bu iki fonksiyonun bölüm türevi aşağıdaki formül ile bulunur:
[f'(x).g(x)-f(x).g'(x)] / g²(x)

İki Fonksiyonun Farkının Türevi
İki fonksiyonun farkının türevi [f(x) – g(x)]’ = f’(x) – g’(x) şeklindedir. İki fonksiyonun farkının türevi alınırken verilen fonksiyonların ayrı ayrı türevleri alınır ve çıkarma işlemi uygulanır.
Köklü Fonksiyonların Türevi
Köklü şekilde verilen fonksiyonlarda kökün türevini almanın yolu bu fonksiyonları üslü halde yazmaktır.
Örneğin, kök x in türevi bulunurken ilk olarak köklü sayı üslü halde yazılır.
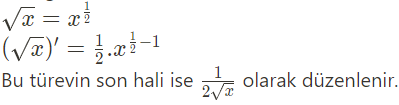
Mutlak Değer Fonksiyonunun Türevi
Mutlak değer fonksiyonunda mutlak değerin içini sıfır yapan değerler fonksiyonun kritik noktalarıdır. Bu kritik noktalarda sağdan ve soldan türev incelenmelidir.
Kritik noktaların dışındaki noktalarda türev alırken mutlak değerin içindeki ifadenin işaretine göre dışarı çıkarıldıktan sonra türev alınır ve türevi sorulan nokta bu aşamadan sonra yerine yazılır.
Bileşke Fonksiyonun Türevi
y = f(x) = (hog)(x) ise, bileşke türev
y’ = f’(x) = h’(g(x)) . g’(x) olur. Burada önemli nokta ‘’için türevi’’ni yani g’(x)’i unutmamaktır.

Zincir Kuralı
y, u değişkenine bağlı
u, v değişkenine bağlı,
v, x değişkenine bağlı türevlenebilen fonksiyonlardır.
y = f(u), u = g(v), v = h(x) olmak üzere;
dy / dx = dy / du * du / dv * dv / dx biçiminde yazılır. Bu kurala zincir kuralı denir.

Ters Fonksiyonun Türevi
Bir f(x) fonksiyonunun tersinin türevi (f^-1)'(y)= 1/f'(x) şeklinde gösterilir.
Logaritmik Fonksiyonların Türevi
f: R → R^+ ve a sayısı 1’den farklı pozitif bir reel sayı olmak üzere,

Üstel Fonksiyonların Türevi
f fonksiyonu a^x formatında bir üstel fonksiyonu olsun. Üstel fonksiyonun türevi f'(x) = a^x * lna şeklinde gösterilir.
Eğer üstel kısımda bir g(x) fonksiyonu varsa; yani f(x) = a^g(x) formatında bir fonksiyonsa f'(x) = a^g(x) * lna * g'(x) olur.
Trigonometrik Fonksiyonların Türevi
Trigonometrik fonksiyonlar türevlerinin tanımlı olduğu aralıklarda,
y = f(x) = sinx ise y’ = cosx
sinx türevi cosx’tir.
y = f(x) = cosx ise y’ = -sinx
cosx türevi eksi sinx’tir.
y = f(x) = tanx ise y’ = sec²x
tan türevi sec karedir.
y = f(x) = cotx ise y’ = -csc²x
cotx türevi eksi csc kare x’tir.
y = f(x) = secx ise y’ = secx . tanx
secx türevi secx çarpı tanx’tir.
y = f(x) = cscx ise y’ = -cscx . cotx
cscx türevi eksi cscx çarpı cotx’tir.
Parçalı Fonksiyonların Türevi
Parçalı fonksiyonlarda türev alırken fonksiyonun kritik noktalarında sağdan ve soldan türevler incelenmelidir.
Parçalı fonksiyon kritik noktalarında sürekli olmalıdır. Aksi halde bu noktalarda türevi yoktur.
Parçalı fonksiyonun kritik noktalarında sağdan ve soldan türev birbirine eşit olmalıdır. Aksi halde bu noktalarda türevi yoktur.
Türevin Geometrik Yorumu
Türev bir fonksiyonun grafiğine çizilen teğetin eğimini hesaplamakta kullanılır. Bir fonksiyonunun x = a noktasındaki türevi, fonksiyonun grafiğine x = a ‘dan çizilen teğetin eğimidir.
Maksimum Minimum Problemleri Nasıl Çözülür?
Türev soruları içindeki minimum maksimum problemlerinin yapılabilmesi için denklem kurma becerimizin iyi olması gerekmektedir.
- Bulunan kök kurulan ilk denklemde yerine yazılır.
- İşaret tablosuna bakılarak soruda istenilen kök seçilir.
- Türev alınıp sıfıra eşitlenir.
- Sorunun tek değişkene bağlı olacak şekilde denklemi kurulur
Not: Çözümleri olabildiğince şekil çizerek yapmaya çalışmalısın.
Ekstremum Noktaları
Bir fonksiyonun yerel maksimum ve yerel minimum noktalarının tamamı, fonksiyonun ekstremum noktaları olarak bilinir.
Yerel Ekstremum Noktası Nasıl Bulunur?
Yerel ekstremum noktalarını bulmak için yerel maksimum noktasına ve yerel minimum noktalarına bakmalıyız.
Mutlak Maksimum Noktası – Mutlak Maksimum Değeri
Bir fonksiyonun tanımlı olduğu aralıktaki en büyük değerini aldığı noktaya mutlak maksimum noktası, en büyük değerine ise mutlak maksimum değeri denir.
Mutlak Minimum Noktası – Mutlak Minimum Değeri
Bir fonksiyonun tanımlı olduğu aralıktaki en küçük değerini aldığı noktaya mutlak minimum noktası, en küçük değerine ise mutlak minimum değeri denir.
Ekstremum noktalarının Özellikleri
- Bir fonksiyonun tanımlı olmadığı noktada ekstremum noktası aranmaz.
- Türevlenebilir bir fonksiyonun ekstremum noktalarından çizilen teğetin eğimi x eksenine paralel olduğundan, bu teğetlerin eğiminin sıfır olduğunu biliyoruz. Bu nedenle türevlenebilir bir fonksiyonun ekstremum noktalarında türev sıfırdır.
- Türevlenebilir bir fonksiyonun türevinin sıfır olduğu her nokta ekstremum noktasıdır demek doğru değildir.
- f’(x) = 0 denkleminin kökü yoksa ya da yalnızca çift katlı kök bulunuyorsa f(x) fonksiyonu daima artan ya da daima azalan bir fonksiyondur. Daima artan ya da daima azalan fonksiyonların ekstremum noktaları yoktur.
- Bir fonksiyonun ekstremum noktalarını nasıl bulacağımızla ilgili bir ipucu: Eğer türevin işareti x_0 noktasında “+” dan “- ” ye değişirse (fonksiyon artan fonksiyondan azalan fonksiyona dönüşürse) x_0 noktası yerel maksimum, “-” den “+” ya değişirse (fonksiyon azalan fonksiyondan artan fonksiyona dönüşürse) x_0 noktası yerel minimum noktasıdır. Eğer türevin işareti değişmezse x_0 noktasında ekstremum yoktur.
Türev – Süreklilik İlişkisi
Türev ve süreklilik kavramları, matematikte önemli olan iki kavramdır. Türev, bir fonksiyonun bir noktadaki anlık değişim oranını temsil ederken, süreklilik ise bir fonksiyonun belirli bir noktada veya aralıkta kesintisiz olup olmadığını ifade eder.
Türevin süreklilikle ilişkisi genellikle şu şekilde ifade edilir: Eğer bir fonksiyon bir noktada türetilmişse, o noktada fonksiyon sürekli olmalıdır. Bu, türevin varlığı için sürekliliğin bir ön koşul olduğu anlamına gelir.
Daha resmi bir ifadeyle, eğer f(x) fonksiyonu c noktasında türevlenebilir ise, )f(x) fonksiyonu c noktasında sürekli olmalıdır. Matematiksel olarak şu şekilde ifade edilebilir:
limx→cf(x)=f(c)
Bu ifade, f(x) fonksiyonunun x değeri c ye yaklaştıkça f(x) in değerinin f(c) ye yaklaştığını belirtir. Eğer bu limit, f(x) fonksiyonu c noktasında tanımlı ise ve bu limit, f(c) değerine eşitse, o zaman f(x) fonksiyonu c noktasında sürekli olarak kabul edilir.
Özetle, türev ve süreklilik arasındaki ilişki, bir fonksiyonun türevlenebilir olduğu bir noktada, o noktada sürekli olması gerektiğini ifade eder.

