In the world of mathematics, functions play a fundamental role. They are powerful tools that help us understand the relationship between different sets of values. Functions can be seen as a process or a rule that takes an input value and produces a corresponding output value. This concept is often visualized as a machine that takes an input and generates an output.
A function can be represented in various ways, such as a formula, a table of values, a graph, or even a diagram. It allows us to understand and analyze the behavior of mathematical phenomena, making it an essential concept in many branches of mathematics, including calculus, algebra, and geometry.
What is a Function?
A function is a special type of relation between two sets of values, where each value in the first set (called the domain) is associated with exactly one value in the second set (called the range). In other words, for every input value, there is a unique output value. This one-to-one correspondence is what distinguishes a function from a general relation.
Functions are often denoted using function notation, such as f(x), where f is the name of the function and x is the input variable. The output value corresponding to a particular input value x is represented as f(x). The function notation allows us to describe the relationship between the input and output values concisely.
It is important to note that not every relation is a function. A relation becomes a function when each input value in the domain is associated with exactly one output value in the range. If there is any input value that has multiple output values, the relation is not a function.
Representation of Functions in Math
Functions can be represented in different ways to help us understand and analyze their properties. The most common representations of functions include sets of ordered pairs, tables, diagrams, and graphs.
Sets of Ordered Pairs
One way to represent a function is by using sets of ordered pairs. In this representation, each ordered pair consists of an input value and its corresponding output value. For example, consider the function f(x) = 2x. The set of ordered pairs for this function would be {(1, 2), (2, 4), (3, 6), …}, where the first value in each pair is the input value and the second value is the output value.
Tables
Another way to represent a function is through a table. A table shows the input values and their corresponding output values in a clear and organized manner. Each row in the table represents an ordered pair. For example, the table for the function f(x) = 2x would look like this:
| x | f(x) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| … | … |
Diagrams
Diagrams can also be used to represent functions, particularly when the function involves a visual relationship between the input and output values. Diagrams can be helpful in understanding geometric or spatial functions. For example, a diagram can be used to represent the relationship between the radius and area of a circle.
Graphical Form
One of the most powerful ways to represent a function is through a graph. A graph visually displays the relationship between the input and output values of a function. The x-axis represents the input values, while the y-axis represents the output values. Each point on the graph represents an ordered pair of input and output values. By connecting these points, we can visualize the behavior of the function.
Graphs can provide valuable insights into the characteristics of a function, such as its domain, range, and behavior at different input values. They allow us to observe patterns, identify key features, and make predictions about the function’s behavior.
Types of Functions
Functions come in various types, each with its own unique characteristics and properties. Let’s explore some of the most common types of functions.
Based on Elements
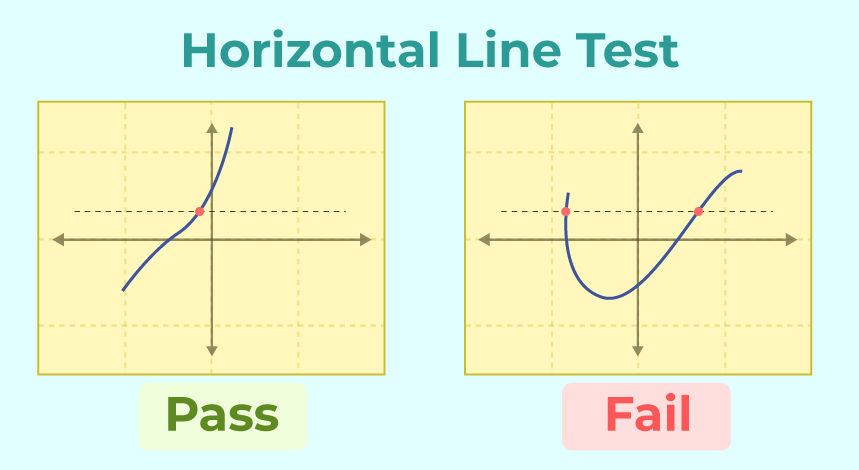
One-One Function
A one-one function, also known as an injective function, is a function in which each element of the domain is associated with a distinct element in the range. In other words, no two different input values can produce the same output value. This means that each output value has a unique pre-image.
For example, consider the function f(x) = x^2. While this function maps every positive and negative number to a unique positive number, it is not a one-one function since both -2 and 2 have the same output value of 4.
Many-One Function
A many-one function is a function in which multiple elements of the domain are associated with the same element in the range. In other words, different input values can produce the same output value. This means that some output values have multiple pre-images.
For example, consider the function f(x) = x^2. In this function, both -2 and 2 have the same output value of 4. Therefore, it is a many-one function.
Onto Function
An onto function, also known as a surjective function, is a function in which every element in the range is associated with at least one element in the domain. In other words, the function covers the entire range.
For example, consider the function f(x) = x^2. In this function, every positive number has a corresponding positive pre-image, and every negative number has a corresponding negative pre-image. Therefore, it is an onto function.

One-One and Onto Function
A one-one and onto function, also known as a bijective function, is a function that is both one-one and onto. In other words, each element in the domain is associated with a distinct element in the range, and the function covers the entire range.
For example, consider the function f(x) = x. In this function, every input value has a unique output value, and the function covers the entire range of real numbers. Therefore, it is a one-one and onto function.
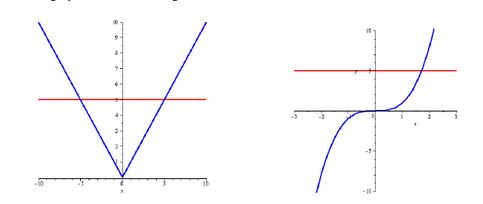
Into Function
An into function is a function in which at least one element of the range is not associated with any element in the domain. In other words, the function does not cover the entire range.
For example, consider the function f(x) = x^2. In this function, there are no negative output values, so it does not cover the entire range of real numbers. Therefore, it is an into function.

Constant Function
A constant function is a function in which all the input values are associated with the same output value. In other words, the function produces a constant output regardless of the input value.
For example, consider the function f(x) = 3. In this function, no matter what the input value is, the output value is always 3. Therefore, it is a constant function.

Based on the Equation
Identity Function
An identity function is a function in which the output value is equal to the input value. In other words, the function preserves the identity of the input.
For example, consider the function f(x) = x. In this function, the output value is the same as the input value. Therefore, it is an identity function.

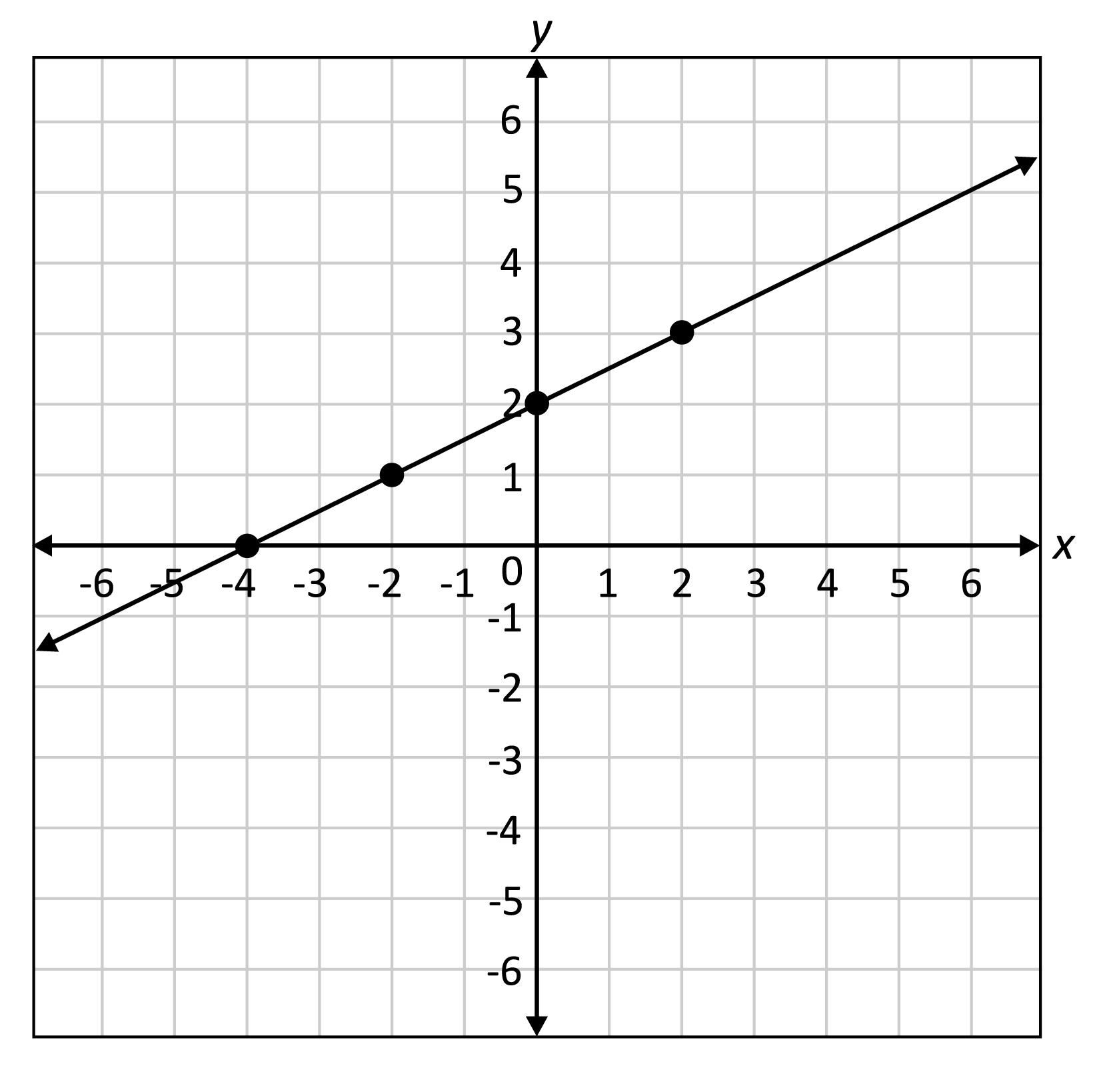
Linear Function
A linear function is a function that can be represented by a straight line on a graph. It has the form f(x) = mx + b, where m is the slope of the line and b is the y-intercept.
For example, consider the function f(x) = 2x + 3. In this function, the slope is 2 and the y-intercept is 3. The graph of this function is a straight line.
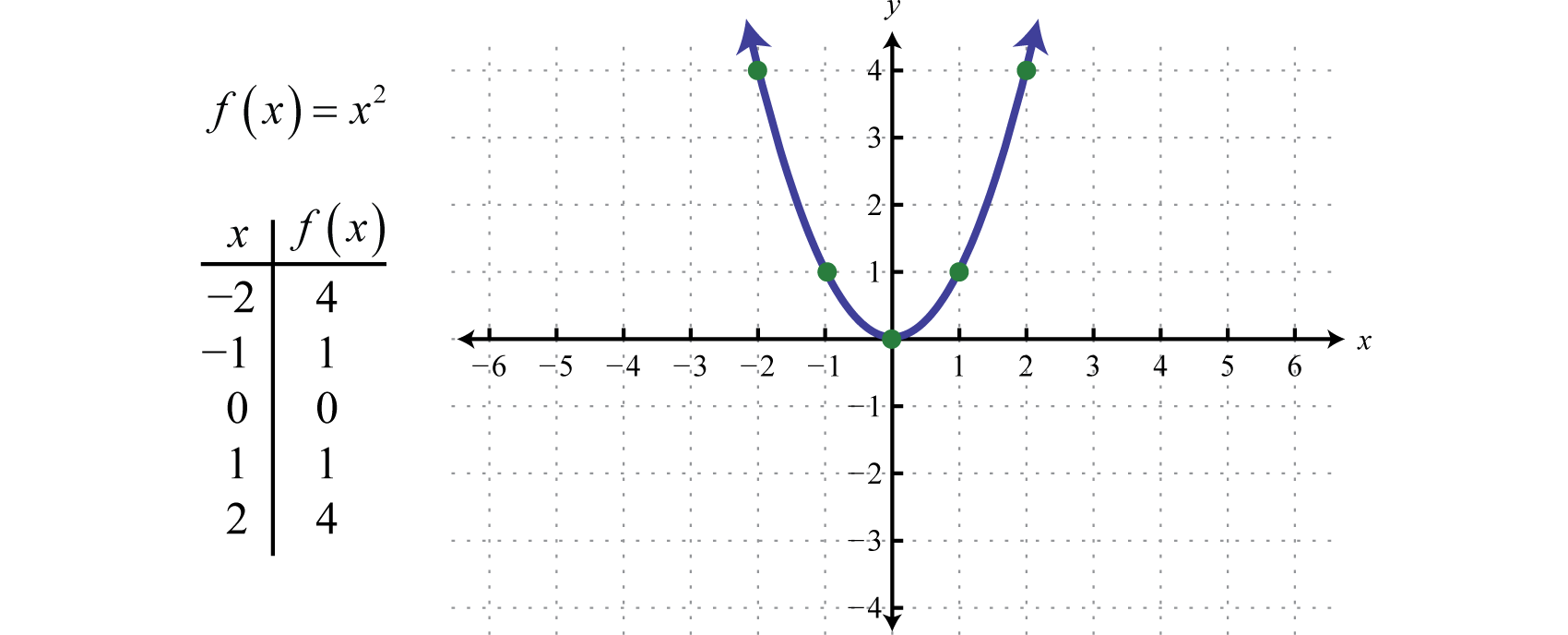
Quadratic Function
A quadratic function is a function that can be represented by a parabola on a graph. It has the form f(x) = ax^2 + bx + c, where a, b, and c are constants and a is not equal to 0.
For example, consider the function f(x) = x^2 + 3x + 2. In this function, the graph is a parabola that opens upwards.
Cubic Function
A cubic function is a function that can be represented by a curve with an S-shape on a graph. It has the form f(x) = ax^3 + bx^2 + cx + d, where a, b, c, and d are constants and a is not equal to 0.
For example, consider the function f(x) = x^3 + 2x^2 + x + 1. In this function, the graph is a curve with an S-shape.
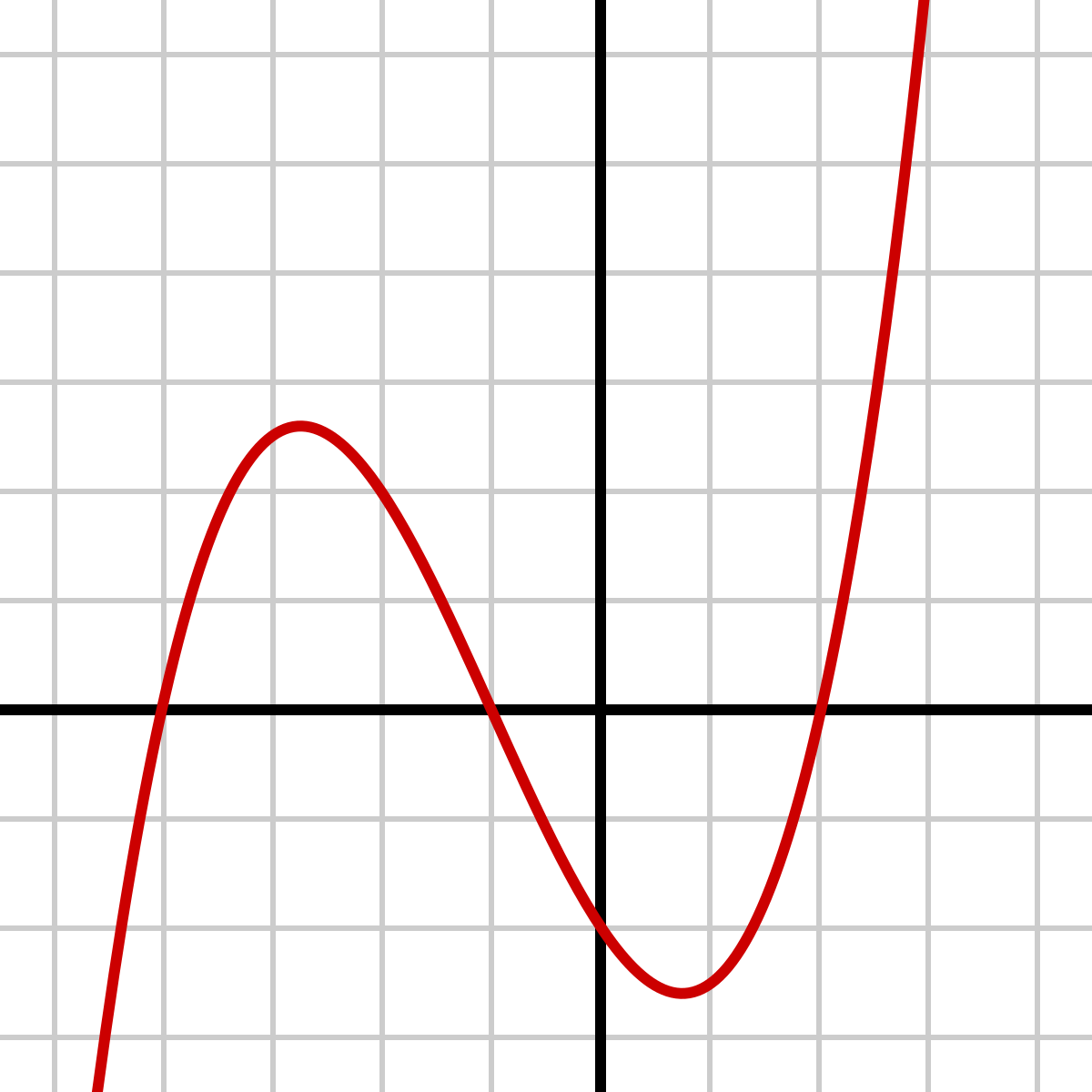
Polynomial Functions
Polynomial functions are functions that can be represented by polynomials. A polynomial is an expression consisting of variables, coefficients, and exponents, combined using addition, subtraction, and multiplication.
For example, the function f(x) = 2x^3 – 3x^2 + 5x + 1 is a polynomial function. It consists of terms with different powers of x.
Based on the Range
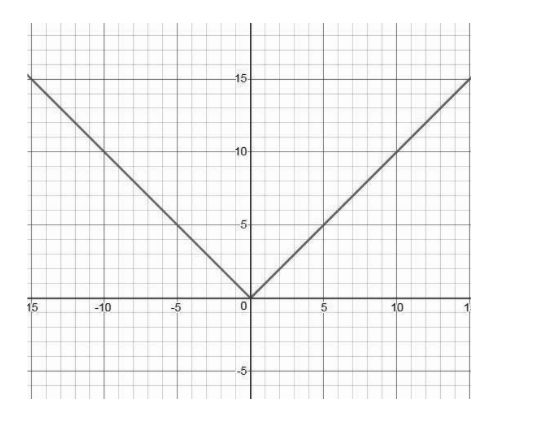
Modulus Function
The modulus function, also known as the absolute value function, returns the non-negative value of a number. It disregards the sign of the input value and only considers its magnitude.
For example, consider the function f(x) = |x|. In this function, the output value is always positive or zero, regardless of the sign of the input value.
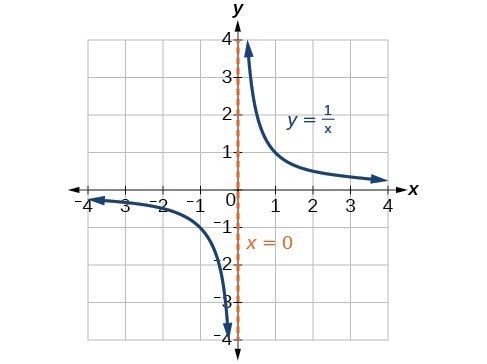
Rational Function
A rational function is a function that can be expressed as a fraction of two polynomial functions. It has the form f(x) = P(x)/Q(x), where P(x) and Q(x) are polynomial functions and Q(x) is not equal to 0.
For example, consider the function f(x) = (2x^2 + 3)/(x + 1). In this function, the output value is the ratio of two polynomial functions.
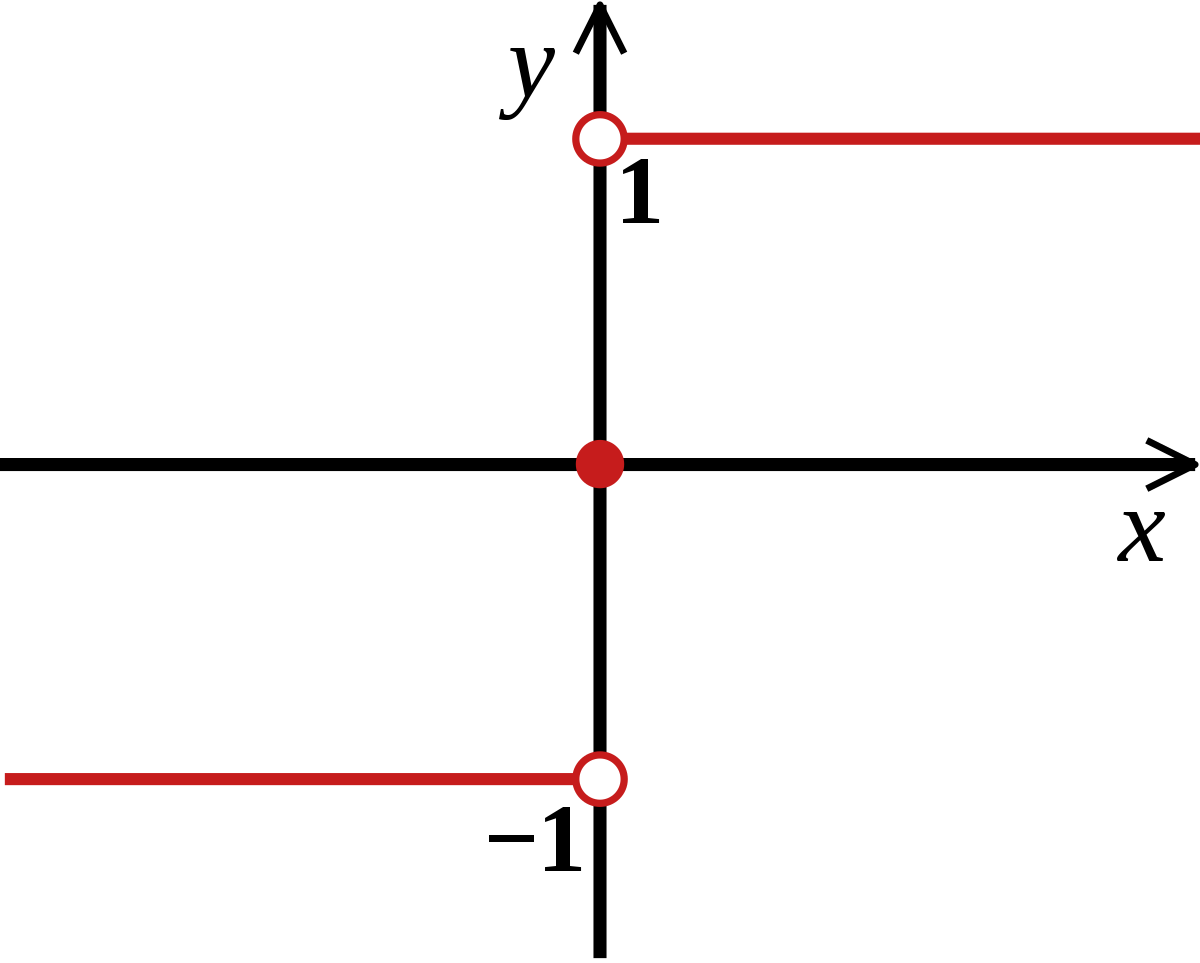
Signum Function
The signum function, also known as the sign function, returns the sign of a number. It indicates whether the input value is positive, negative, or zero.
For example, consider the function f(x) = sign(x). In this function, the output value is -1 for negative input values, 1 for positive input values, and 0 for zero input values.
Even and Odd Functions
Even and odd functions are special types of functions that exhibit symmetry. An even function is symmetric with respect to the y-axis, while an odd function is symmetric with respect to the origin.
For example, the function f(x) = x^2 is an even function, as it remains unchanged when reflected about the y-axis. The function f(x) = x^3 is an odd function, as it remains unchanged when reflected about the origin.

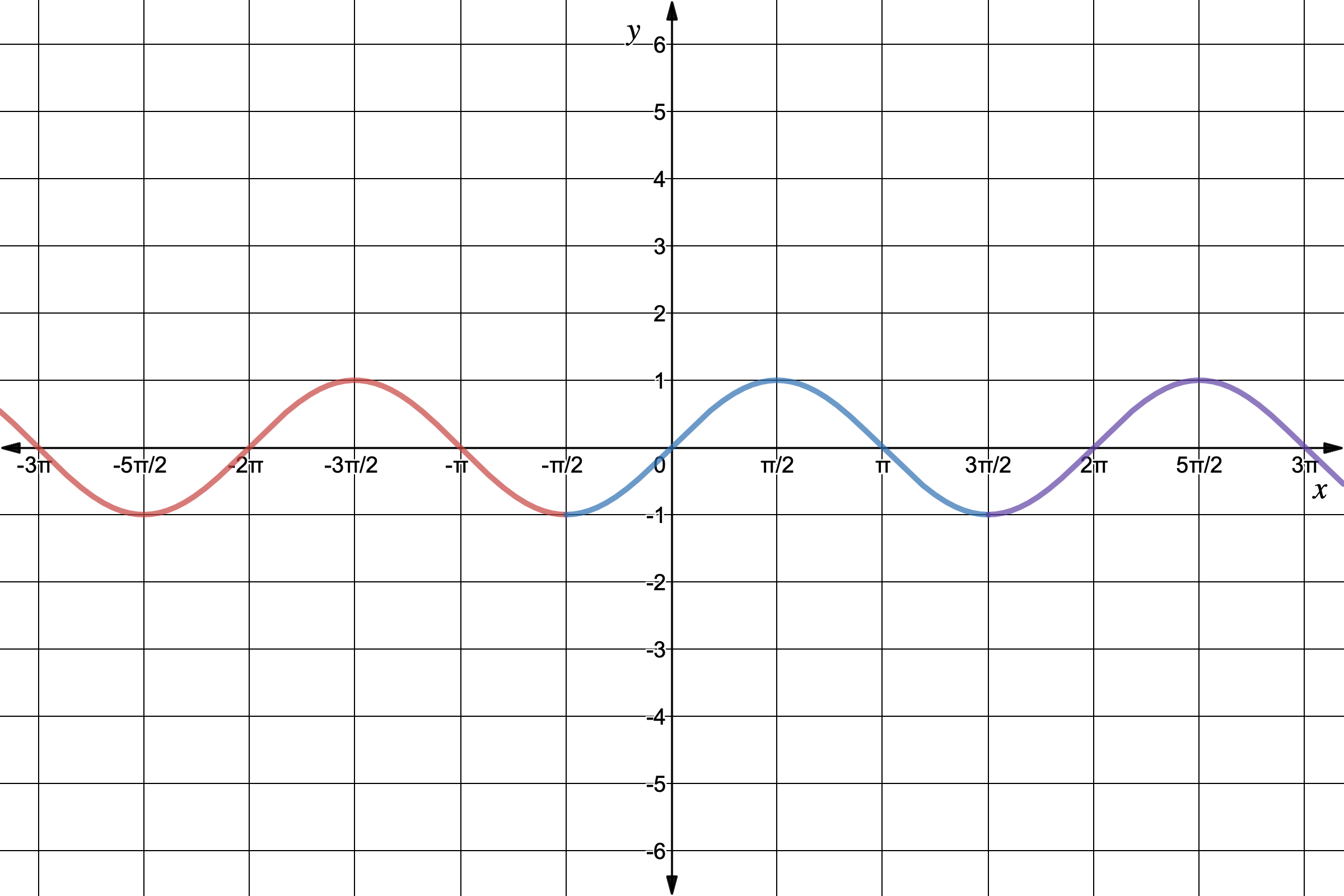
Periodic Functions
Periodic functions are functions that repeat their values at regular intervals. They exhibit a pattern that repeats indefinitely.
For example, the trigonometric functions sine and cosine are periodic functions. They repeat their values every 2π radians or 360 degrees.
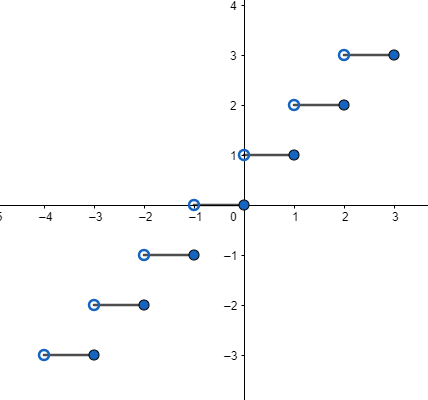
Greatest Integer Function
The greatest integer function, also known as the floor function, returns the largest integer less than or equal to a given input value. It effectively rounds the input value down to the nearest integer.
For example, consider the function f(x) = ⌊x⌋. In this function, the output value is the largest integer that is less than or equal to the input value.

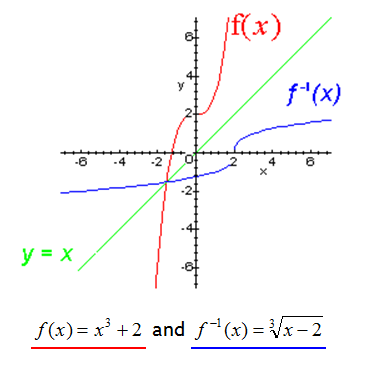
Inverse Function
An inverse function is a function that “undoes” the action of another function. It reverses the input and output values of the original function.
For example, consider the function f(x) = 2x. The inverse function of f(x) is f^(-1)(x) = x/2, which undoes the action of doubling the input value.
Smallest Integer Functions
The smallest integer function, also known as the ceiling function, returns the smallest integer greater than or equal to a given input value. It effectively rounds the input value up to the nearest integer.
For example, consider the function f(x) = ⌈x⌉. In this function, the output value is the smallest integer that is greater than or equal to the input value.
Composite Functions
Composite functions are functions that are formed by combining two or more functions. The output of one function becomes the input of another function.
For example, consider the functions f(x) = 2x and g(x) = x + 3. The composite function f(g(x)) is formed by substituting g(x) into f(x), resulting in f(g(x)) = 2(x + 3).
Based on the Domain
Algebraic Functions
Algebraic functions are functions that can be expressed using algebraic operations, such as addition, subtraction, multiplication, division, and exponentiation.
For example, the functions f(x) = 2x + 3 and g(x) = x^2 are algebraic functions, as they can be expressed using algebraic operations.
Trigonometric Functions
Trigonometric functions are functions that involve the ratios of the sides of a right triangle. They include functions such as sine, cosine, and tangent.
For example, the function f(x) = sin(x) is a trigonometric function, as it represents the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.
Logarithmic Functions
Logarithmic functions are functions that involve the logarithm operation. They represent the inverse relationship of exponential functions.
For example, the function f(x) = log(x) is a logarithmic function, as it represents the power to which a base must be raised to obtain a given value.
Exponential Functions
Exponential functions are functions that involve the exponential operation. They represent the growth or decay of a quantity over time.
For example, the function f(x) = 2^x is an exponential function, as it represents the growth of a quantity by a factor of 2 for each unit increase in the input value.
Composition of Functions
Composition of functions is the process of combining two or more functions to create a new function. The output of one function becomes the input of another function.
For example, consider the functions f(x) = 2x and g(x) = x + 3. The composite function f(g(x)) is formed by substituting g(x) into f(x), resulting in f(g(x)) = 2(x + 3) = 2x + 6.
Composition of functions allows us to study the behavior and properties of complex functions by breaking them down into simpler components. It enables us to analyze how changes in one function affect the overall behavior of the composite function.
Graphing Functions
Graphing functions is a powerful tool that allows us to visualize the relationship between the input and output values of a function. By plotting the points on a graph, we can observe patterns, identify key features, and make predictions about the function’s behavior.
To graph a function, we typically use a coordinate plane, where the x-axis represents the input values and the y-axis represents the output values. Each point on the graph corresponds to an ordered pair of input and output values. By connecting these points, we can create a visual representation of the function.
Graphs provide us with valuable information about the characteristics of a function, such as its domain, range, symmetry, and behavior at different input values. They allow us to analyze the function’s properties, identify key points, determine intervals of increase or decrease, and locate any intercepts or asymptotes.
Function in Algebra
In algebra, a function is represented as an equation for which any x that can be put into the equation will produce exactly one output, y. It is denoted as y = f(x), where x is the independent variable and y is the dependent variable.
Algebraic functions are functions that can be expressed using algebraic operations, such as addition, subtraction, multiplication, and division. They involve variables and coefficients, which can take on different values.
For example, consider the function f(x) = 2x + 1. In this function, the input value x is multiplied by 2, and then 1 is added to the result. The output value y is determined by the value of x.
Functions in algebra allow us to model real-world situations, solve equations, and analyze relationships between variables. They are fundamental to the study of algebra and provide a basis for more advanced mathematical concepts.
The Domain of a Function
The domain of a function is the set of all possible input values for which the function is defined. It represents the values that can be put into the function and produce a valid output.
The domain of a function can vary depending on the type of function and the context in which it is defined. In some cases, the domain may be restricted to a specific range of values, while in others, it may include all real numbers.
For example, consider the function f(x) = √x. In this function, the domain is restricted to non-negative real numbers, as the square root of a negative number is not defined in the real number system.
The domain of a function is important because it determines the set of values that we can input into the function and analyze. It helps us understand the behavior and properties of the function and ensures that we are working with valid inputs.
The Range of a Function
The range of a function is the set of all possible output values that the function can produce. It represents the values that can be obtained from the function by varying the input values.
The range of a function can vary depending on the type of function and the context in which it is defined. In some cases, the range may be restricted to a specific set of values, while in others, it may include all real numbers.
For example, consider the function f(x) = x^2. In this function, the range is all non-negative real numbers, as the square of any real number is non-negative.
The range of a function is important because it helps us understand the set of values that the function can produce. It allows us to analyze the behavior and properties of the function and determine the possible output values for different input values.
Function Notation
Function notation is a way to represent functions using mathematical symbols and expressions. It allows us to describe the relationship between the input and output values of a function in a concise and standardized manner.
In function notation, a function is typically denoted by a letter, such as f, g, or h, followed by parentheses. The input variable is placed inside the parentheses, and the output value is represented by the expression to the right of the function name.
For example, consider the function f(x) = 2x + 3. In this function, f is the name of the function, and x is the input variable. The expression 2x + 3 represents the output value corresponding to a particular input value x.
Function notation allows us to perform operations on functions, such as composition, differentiation, and integration. It provides a standardized way to describe and manipulate functions, making it easier to communicate and work with mathematical concepts.
Solved Examples on Function
Let’s solve a few examples to further illustrate the concept of functions.
Example 1: Find the value of f(3) for the function f(x) = 2x – 1.
Solution: To find the value of f(3), we substitute x = 3 into the function: f(3) = 2(3) – 1 = 6 – 1 = 5
Therefore, the value of f(3) is 5.
Example 2: Determine the domain of the function f(x) = √(4 – x^2).
Solution: To find the domain of the function, we need to consider the values of x that make the expression under the square root non-negative. In this case, we have 4 – x^2 ≥ 0.
Solving this inequality, we get: 4 – x^2 ≥ 0 (x – 2)(x + 2) ≥ 0
The critical points are x = -2 and x = 2. We can test the intervals to determine the sign of the expression: For x < -2, both factors are negative, so the expression is positive. For -2 < x < 2, the factor (x – 2) becomes positive, while the factor (x + 2) remains negative, so the expression is negative. For x > 2, both factors are positive, so the expression is positive.
Therefore, the domain of the function is -2 ≤ x ≤ 2.
Example 3: Find the composite function (g ∘ f)(x) for the functions f(x) = 2x + 3 and g(x) = x^2.
Solution: To find the composite function (g ∘ f)(x), we substitute f(x) into g(x): (g ∘ f)(x) = g(f(x)) = g(2x + 3) = (2x + 3)^2 = 4x^2 + 12x + 9
Therefore, the composite function (g ∘ f)(x) is 4x^2 + 12x + 9.
These examples demonstrate how functions can be used to solve problems and analyze mathematical relationships. By understanding the concepts of functions and their notation, we can apply them to various real-world and mathematical scenarios.
How Kunduz Can Help You Learn Function?
At Kunduz, we understand the importance of mastering the concept of functions in mathematics. That’s why we are committed to providing comprehensive and accessible resources to help you learn and understand functions effectively.
With Kunduz, you can gain a solid foundation in function notation, types of functions, graphing functions, and much more. Our step-by-step approach and clear explanations will guide you through complex concepts, making learning enjoyable and accessible.
