The concept of the z-score is an essential tool in statistics and probability theory. It allows us to understand how a particular data point relates to the mean and standard deviation of a given population. In this article, we will explore the z-score in detail, including its definition, formula, interpretation, and applications. We will also dive into the concept of the standard normal distribution and its relationship with the z-score. Additionally, we will provide a comprehensive z-score table and walk you through how to calculate and use z-scores.
An Introduction to the Z-Score Table
The z-score, also known as the standard score, is a statistical measure that quantifies how many standard deviations a given data point is from the mean of a distribution. It provides a standardized way of comparing data points from different distributions. The z-score can be positive or negative, indicating whether the data point is above or below the mean, respectively. A z-score of 0 represents a data point that is equal to the mean.
To fully understand the significance of a z-score, we need to delve into the concept of the standard normal distribution.
What is the Standard Normal Distribution?
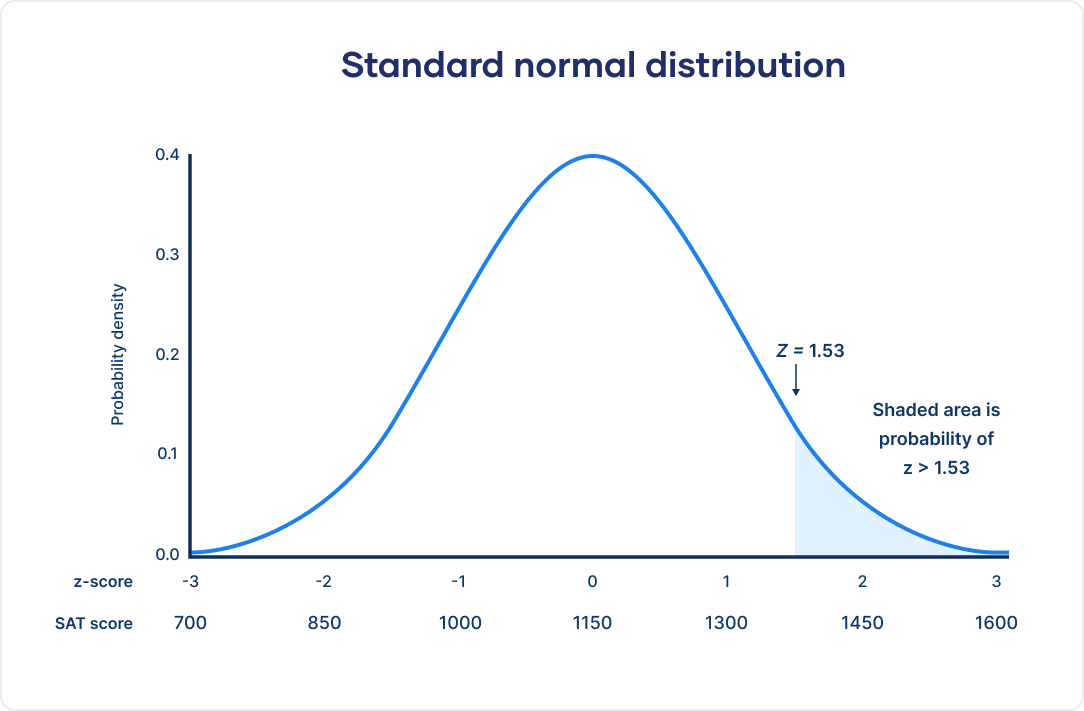
The standard normal distribution, also known as the Z-distribution or the Gaussian distribution, is a specific form of the normal distribution. It has a mean of 0 and a standard deviation of 1. The standard normal distribution is symmetric, with the majority of the data falling within a range of -3 to 3 standard deviations from the mean. This distribution is often represented by a bell-shaped curve.
The z-score allows us to convert any normal distribution to the standard normal distribution. By doing so, we can use the z-score table to find probabilities associated with specific z-scores.
Z-Score Formula, How to Find Z-Score?
The z-score formula calculates the z-score for a given data point in relation to the mean and standard deviation of a distribution. The formula is as follows:
z = (x – μ) / σ
Where:
- z is the z-score
- x is the data point
- μ is the mean of the distribution
- σ is the standard deviation of the distribution
Let’s take an example to illustrate how to find the z-score. Suppose we have a test score of 80, a mean test score of 75, and a standard deviation of 10. We can calculate the z-score using the formula:
z = (80 – 75) / 10 = 0.5
This means that the test score of 80 is 0.5 standard deviations above the mean.
How to Interpret Z-Score?
Interpreting the z-score is crucial for understanding the significance of a data point in relation to the distribution. Here are some key points to remember:
- A z-score greater than 0 indicates that the data point is above the mean.
- A z-score less than 0 indicates that the data point is below the mean.
- A z-score of 0 indicates that the data point is equal to the mean.
- The magnitude of the z-score represents the number of standard deviations the data point is from the mean. For example, a z-score of 1 means the data point is 1 standard deviation away from the mean.
Using the standard normal distribution table, we can determine the probability associated with a specific z-score.
Standard Normal Probabilities
The standard normal distribution table, also known as the z-score table or the unit normal table, is a mathematical table that provides the cumulative probabilities associated with specific z-scores. It enables us to find the area under the curve to the left of a given z-score.
The z-score table is divided into two types: the positive z-score table and the negative z-score table. The positive z-score table is used to find the probabilities for z-scores greater than 0, while the negative z-score table is used for z-scores less than 0.
The z-score table presents the cumulative probability associated with a particular z-score. The rows of the table represent the whole number and tenth place of the z-score, while the columns represent the hundredth place.
To use the z-score table, locate the row corresponding to the first two digits of the z-score and the column corresponding to the third digit. The intersection of the row and column will give you the cumulative probability associated with that z-score.

How to Calculate Z-Scores?
Calculating z-scores involves finding the number of standard deviations a data point is from the mean. Here is a step-by-step guide on how to calculate z-scores:
- Determine the data point you want to calculate the z-score for.
- Find the mean and standard deviation of the distribution.
- Subtract the mean from the data point.
- Divide the result by the standard deviation.
Let’s go through an example to illustrate the calculation of z-scores. Suppose we have a dataset of exam scores with a mean of 70 and a standard deviation of 15. We want to calculate the z-score for a student who scored 85 on the exam.
Step 1: Determine the data point: 85
Step 2: Find the mean: 70
Step 3: Subtract the mean: 85 – 70 = 15
Step 4: Divide by the standard deviation: 15 / 15 = 1
The z-score for the student who scored 85 on the exam is 1. This means that the student’s score is 1 standard deviation above the mean.
How to Use the Z-Score Table?
The z-score table is a valuable tool for finding probabilities associated with specific z-scores. To use the z-score table, follow these steps:
- Identify the z-score you want to find the probability for.
- Determine whether the z-score is positive or negative.
- Locate the row in the z-score table that corresponds to the first two digits of the z-score.
- Locate the column that corresponds to the third digit of the z-score.
- Find the intersection of the row and column. This value represents the cumulative probability associated with the z-score.
For example, let’s say we want to find the probability associated with a z-score of -1.5. Since the z-score is negative, we will use the negative z-score table. We locate the row for -1.5 and the column for 0.00. The intersection of the row and column gives us the cumulative probability of 0.0668. This means that approximately 6.68% of the data falls below a z-score of -1.5.
Applications of Z Score
The z-score has various applications in statistics and data analysis. Some common applications include:
- Hypothesis Testing: Z-scores are used to calculate critical values and p-values in hypothesis testing.
- Quality Control: Z-scores are used to monitor and control the quality of manufacturing processes.
- Risk Assessment: Z-scores are used to assess the risk associated with investment portfolios or financial instruments.
- Standardization: Z-scores are used to standardize data and make meaningful comparisons across different populations.
- Outlier Detection: Z-scores are used to identify outliers in datasets.
The z-score provides a standardized measure that allows us to compare data points from different distributions and make informed decisions based on their relative positions.
Normal Distribution VS Standard Normal Distribution
While the normal distribution and the standard normal distribution are related, they have some key differences. The normal distribution can have any mean and standard deviation, whereas the standard normal distribution has a mean of 0 and a standard deviation of 1.
The standard normal distribution serves as a reference distribution, allowing us to standardize any normal distribution by converting it to the standard normal distribution. This standardization enables us to use the z-score table to find probabilities associated with specific z-scores.
Area Under Standard Normal Curve
The area under the standard normal curve represents the probability of observing a value less than or equal to a given z-score. The standard normal curve is symmetric, with the mean at the center and the standard deviation determining the spread of the curve.
The z-score table provides the cumulative probabilities associated with specific z-scores, which represent the area under the standard normal curve to the left of those z-scores. By using the z-score table, we can find the probability of observing a value within a certain range or above/below a specific z-score.
Characteristics of Standard Normal Distribution
The standard normal distribution has several characteristics that make it a useful tool in statistical analysis:
- Symmetry: The standard normal distribution is symmetric, with the mean at the center. This symmetry allows for easy calculation of probabilities and percentiles.
- Mean and Standard Deviation: The mean of the standard normal distribution is 0, and the standard deviation is 1. These values determine the shape and spread of the distribution.
- Empirical Rule: The standard normal distribution follows the empirical rule, also known as the 68-95-99.7 rule. Approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations, and 99.7% falls within three standard deviations.
- Standardization: The standard normal distribution allows for the standardization of data by converting it to z-scores. This standardization enables meaningful comparisons across different populations.
- Cumulative Probabilities: The z-score table provides the cumulative probabilities associated with specific z-scores, allowing for quick calculation of probabilities for any normal distribution.
The characteristics of the standard normal distribution make it a valuable tool in statistical analysis and hypothesis testing.
Z Score Table Types
The z-score table is divided into two types: the positive z-score table and the negative z-score table. These tables provide the cumulative probabilities associated with specific z-scores.
Negative Z Score Table
The negative z-score table is used to find the probabilities associated with negative z-scores. It provides the cumulative probabilities for z-scores that are below the mean of the distribution.
To use the negative z-score table, locate the row that corresponds to the first two digits of the z-score and the column that corresponds to the third digit. The intersection of the row and column gives you the cumulative probability associated with the negative z-score.
Positive Z Score Table
The positive z-score table is used to find the probabilities associated with positive z-scores. It provides the cumulative probabilities for z-scores that are above the mean of the distribution.
To use the positive z-score table, follow the same steps as with the negative z-score table. Locate the row that corresponds to the first two digits of the z-score and the column that corresponds to the third digit. The intersection of the row and column gives you the cumulative probability associated with the positive z-score.
Using the appropriate z-score table allows for quick and accurate calculation of probabilities associated with specific z-scores.
Solved Examples on Z-Score
Let’s solve a few examples to demonstrate how to apply z-scores in real-world scenarios.
Example 1: Suppose the heights of a population of adults follow a normal distribution with a mean of 170 cm and a standard deviation of 10 cm. What is the z-score for an adult who is 180 cm tall?
Solution: We can use the z-score formula to calculate the z-score:
z = (x – μ) / σ z = (180 – 170) / 10 z = 1
The z-score for an adult who is 180 cm tall is 1, indicating that the height is 1 standard deviation above the mean.
Example 2: The scores on a math test follow a normal distribution with a mean of 75 and a standard deviation of 5. What percentage of students scored above 85?
Solution: We can use the z-score formula to calculate the z-score for a score of 85:
z = (x – μ) / σ z = (85 – 75) / 5 z = 2
To find the percentage of students who scored above 85, we can use the positive z-score table. The table shows that the area to the left of a z-score of 2 is 0.9772. Therefore, the percentage of students who scored above 85 is approximately 1 – 0.9772 = 0.0228, or 2.28%.
Example 3: In a company, the average salary is $50,000 with a standard deviation of $5,000. An employee earning $60,000 would have a z-score calculated as:
- z = (x – μ) / σ
- z = (60000 – 50000) / 5000 = 2
This indicates that the employee’s salary is two standard deviations above the mean.
These examples demonstrate how z-scores can be used to calculate the relative position of data points in a distribution and find probabilities associated with specific values.
How Kunduz Can Help You Learn Z-Score?
If you’re looking to enhance your understanding of z-scores and their applications, Kunduz is here to help. Our comprehensive online learning platform offers a wide range of resources, including step-by-step tutorials, practice problems, and interactive quizzes. With Kunduz, you can master the concept of z-scores and confidently apply them to various statistical analyses.
At Kunduz, we believe that learning should be accessible to everyone. That’s why we offer affordable subscription plans that provide unlimited access to our extensive collection of educational materials. Whether you’re a student, educator, or professional, Kunduz can empower you with the knowledge and skills needed to excel in your academic and professional pursuits.
Don’t let z-scores intimidate you. Join Kunduz today and embark on a journey of discovery and mastery of statistical concepts. Let us be your guide to success in the world of statistics.
