(a) Find the interval(s) on which is increasing. Recall the

Last updated: 7/13/2022

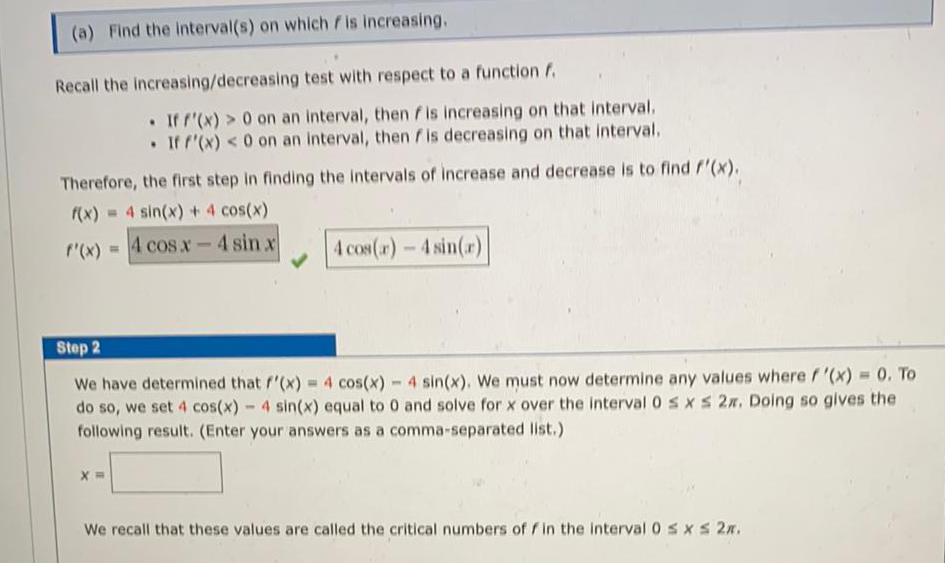
(a) Find the interval(s) on which is increasing. Recall the increasing/decreasing test with respect to a function f. • If f'(x) > 0 on an interval, then fis increasing on that interval. • If f'(x) < 0 on an interval, then fis decreasing on that interval. Therefore, the first step in finding the intervals of increase and decrease is to find f'(x). f(x) = 4 sin(x) + 4 cos(x) f'(x) = 4 cos.x - 4 sin x Step 2 We have determined that f'(x) = 4 cos(x) - 4 sin(x). We must now determine any values where f'(x) = To do so, we set 4 cos(x) - 4 sin(x) equal to 0 and solve for x over the interval 0 ≤ x ≤ 2x. Doing so gives the following result. (Enter your answers as a comma-separated list.) x= We recall that these values are called the critical numbers of f in the interval 0 ≤ x ≤ 2x.