Application of derivatives Questions and Answers

Math
Application of derivativesA baseball is travelling on a path given by the equation y 0 011x 1 15x 1 22 The profile of the bleachers in the outfield can be modelled with the equation y 0 6x 72 All distances are in metres a Determine the maximum height of the ball b Does the ball reach the bleachers for a home run Justify your answer

Math
Application of derivativesA rectangular solid with a square base has a volume of 1 728 cubic inches Let w represent the length of the sides of the square base and let h represent the height of the solic a Determine the dimensions in inches that yield the minimum surface area W h in in in b Find the minimum surface area in in

Math
Application of derivativesO cm cm cm cm cm s The function V r models the volume of a basketball that is deflating due to a puncture If V r is measured in cm and r is measured in cm what are the units of V r 1 point rm s

Math
Application of derivativesGiven this function f x 35 arcsin 11 an equation for the line tangent to the graph of y f x at the point where x Y is

Math
Application of derivativesApie is removed from your oven with an internal temperature of 165 F It is placed on your counter to cool The temperature of the room is 65 F If the temperature is 140 F after half an hour how much time will have passed when the temperature of the pie will be equal to 95 F Note Round to the nearest hundredth of an hour

Math
Application of derivativesWhich of the following would not be a representation of the differentiable function f where f 5 3 6 points O The slope of y f x at x 5 is 3 O The instantaneous rate of change at x 5 of f x is 3 O f 3 h f 3 lim h 0 h 5 The slope of a line tangent to the graph of f at x 5 is 3

Math
Application of derivatives9 A farmer has 5000 meters of fencing to enclose a rectangular field and subdivide it into three equal plots The enclosed area is to be a maximum Determine the dimensions of one plot of land to the nearest meter

Math
Application of derivativesFarmer Ed has 650 meters of fencing and wants to enclose a rectangular plot that borders on a river If Farmer Ed does not fence the side along the river find the length and width of the plot that will maximize the area What is the largest area that can be enclosed The width labeled x in the figure is 162 5 meters Type an integer or decimal The length labeled 650 2x in the figure is 325 meters Type an integer or decimal The largest area that can be enclosed is Type an integer or decimal square meters CEL
Math
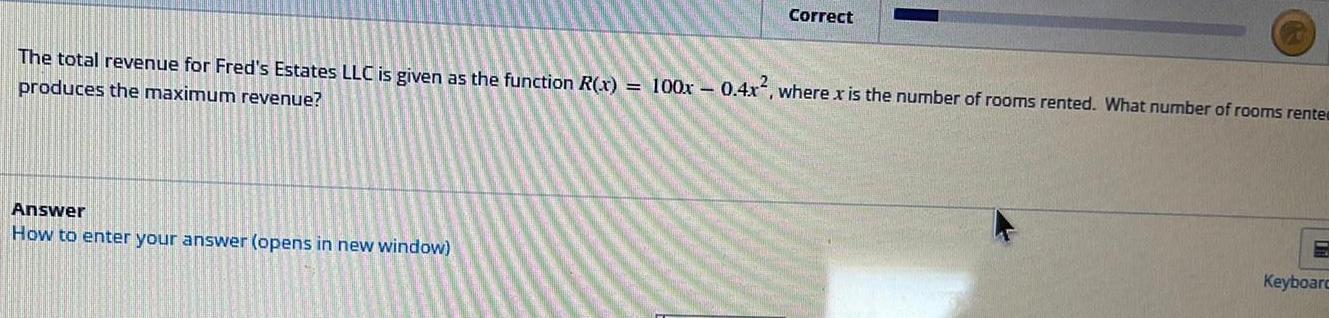
Application of derivativesCorrect The total revenue for Fred s Estates LLC is given as the function R x 100x 0 4x where x is the number of rooms rented What number of rooms rente produces the maximum revenue Answer How to enter your answer opens in new window Keyboard

Math
Application of derivatives1 2 A drone flies in a straight line with a positive velocity v t in miles per hour at time t hours where v is a differentiable function of t Selected values of v t are shown in the table t hours 2 v t miles per hour 2 1 2 5 2 1 0 1 3 4 5 6 1 7 1 5 1 5 1 6 Based on the values in the table at is the smallest number of instances at which the acceleration of the plane could equal zero on the open interval 0 c 6 1 point
Math
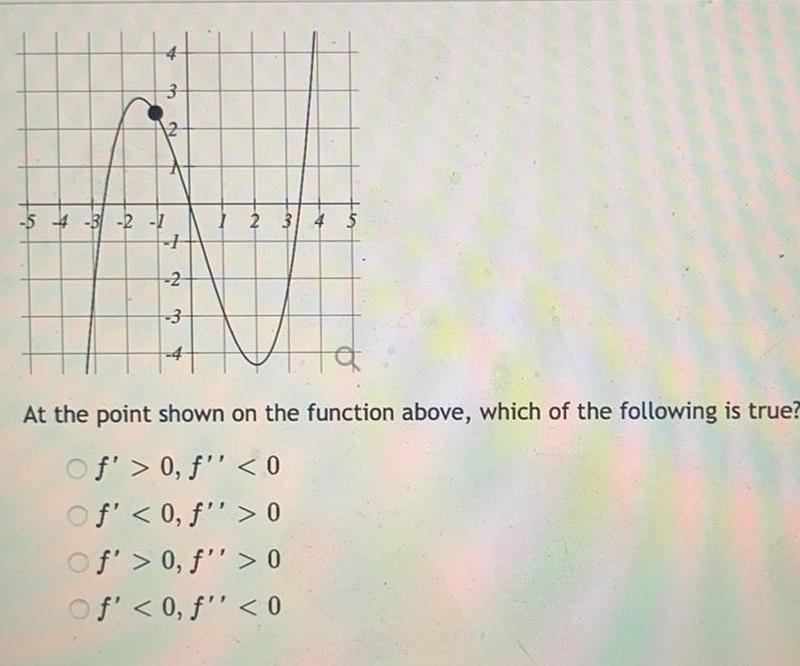
Application of derivativesf 3 12 5 4 3 2 1 2 3 1 2 3 4 5 At the point shown on the function above which of the following is true Of 0 f 0 Of 0 f 0 Of 0 f 0 Of 0 f 0

Math
Application of derivativesProblem 4 10 Points Words Words Words part 1 5 points each You boss decides to launch a new product cerebrum vastatorem and you are tasked with finding the optimal price and quantity The revenue function is R 5p 1000p where R is the revenue and p is the price Find the revenue maximizing price and the maximum revenue and graph it Remember that you can label the scale for your graph

Math
Application of derivatives1000 The population of deer in a park can be modeled by P t where P t is the 1 60e t number of deer and t 0 is time in years since the deer were introduced to the park A Eventually how many deer will be in the park Explain your reasoning B Evaluate P 8 P 3 8 3 problem using correct units Explain the meaning of this value in the context of the

Math
Application of derivativesBryan has 180 feet of fencing to fence off his rectangular garden He will use the wall of his house as one side of the garden garden 1 Write an equation to find the area of the garden 2 What dimensions create the garden with the greatest area 3 What is the greatest area UPLOAD

Math
Application of derivatives8 A radioactive isotope is decaying at a rate of 18 every hour Currently there are 100 grams of the substance Part B How much will be left one day from now Round your answer to the nearest hundredth

Calculus
Application of derivativesA twice differentiable function f is defined for all real numbers x The derivative of the function f and its second derivative have the properties and various values of x as indicated in the table 6 f x positive DNE negative 0 f x positive DNE positive 0 X 0 x 3 3 3 x 6 6 x 9 negative negative Part A Find all values of x at which f has a relative extrema on the interval 0 9 Determine whether f has a relative maximum or a relative minimum at each of these values Justify your answer 10 points Part B Determine where the graph of f is concave up and where it is concave down Support your answer 10 points Part C Find any points of inflection of f Show the analysis that leads to your answer 10 points

Math
Application of derivativesThe function h represents the height of an object t seconds after it is launched into the air. The function is defined by h(t) = -5t² + 20t+18. Height is measured in meters.
1) When will the object hit the ground? (round to the nearest hundredth)
seconds
2) At what 2 times does the object occupy a height of 33 meters?
seconds and seconds
3) When does the object reach its maximum
height? seconds
4) What is the maximum height that the
object reaches? meters

Math
Application of derivativesThe number of mosquitoes M(x), in millions, in a certain area depends on the June rainfall x, in inches: M(x) = 4x-x². What rainfall produces the maximum number of mosquitoes?
A. 16 inches
B. 0 inches
C. 2 inches
D. Maximum number of mosquitoes does not exist
E. 4 inches
Math
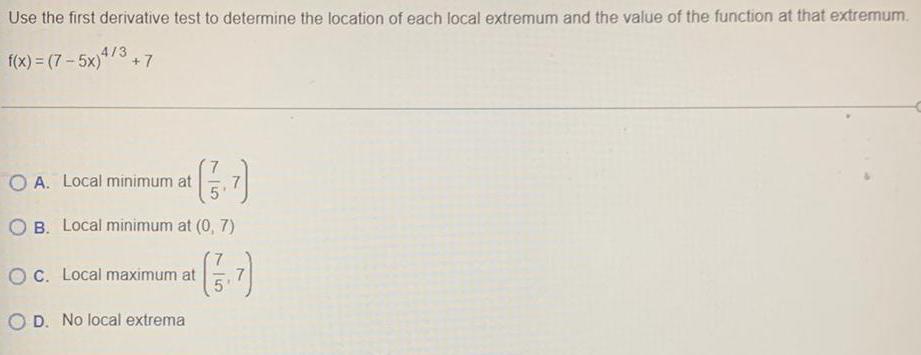
Application of derivativesUse the first derivative test to determine the location of each local extremum and the value of the function at that extremum.
f(x) = (7-5x)4/3 +7
A. Local minimum at (7/5,7)
B. Local minimum at (0,7)
C. Local maximum at (7/5,7)
D. No local extrema
Math
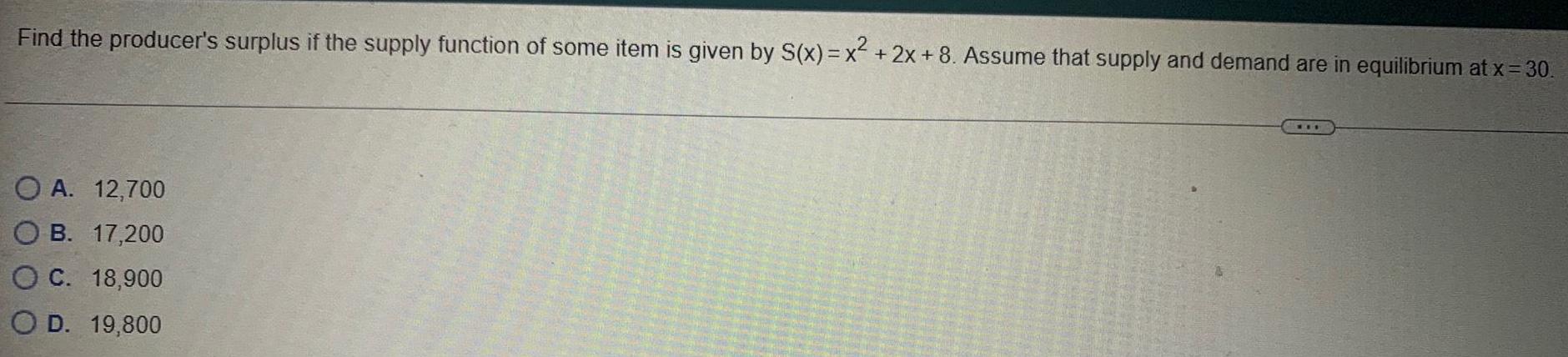
Application of derivativesFind the producer's surplus if the supply function of some item is given by S(x)=x²+2x+8. Assume that supply and demand are in equilibrium at x = 30.
A. 12,700
B. 17,200
C. 18,900
D. 19,800
Math
Application of derivativesGiven that the variable cost is given by 2x² + 4x and fixed cost is 5000. Determine the:
A. total cost function
B. marginal cost function
C. average cost function
D. average cost when x = 5

Math
Application of derivativesTaylor is on one side of a river that is 50 meters wide and wants to reach a point 200 meters downstream on the opposite side as quickly as possible by swimming in a diagonal line across the river and then running the rest of the way. Where should Taylor exit the water if she can swim at 1.5 meters per second and run at 4 meters per second.

Math
Application of derivativesFind the minimum value of the objective function f(x, y) = x² + y²
subject to the constraint y = r +1
(a) Use the constraint to rewrite the objective function with only a single variable. Then use
single-variable calculus techniques to find the absolute minimum of the new function.

Math
Application of derivativesGiven the function g(x) = 6x³ + 45x² + 72x, find the first derivative, g'(x) = 0 when a = 4, that is, g'(-4) = 0.
Now, we want to know whether there is a local minimum or local maximum at z = 4, so we will use the second derivative test.
Find the second derivative, g''(x).
g''(x) =
Evaluate g''(-4).
g''(-4)=
Based on the sign of this number, does this mean the graph of g(x) is concave up or concave down at a = - 4?
At = - 4 the graph of g(x) is concave
Based on the concavity of g(x) at x =
At z = - 4 there is a local
![Consider the differential equation
dy/dx = x² (y + 1).
Sketch a slope field for the given differential equation on your paper for the domain [-3, 3] and the range [-3, 3].
Part A: List five coordinates and the corresponding slope of their segments.
Part B: Using the slope field that you drew, describe all points in the xy-plane for which the slopes are negative.](https://media.kunduz.com/media/sug-question/raw/77435227-1660484498.63686.jpeg?w=256)
Math
Application of derivativesConsider the differential equation
dy/dx = x² (y + 1).
Sketch a slope field for the given differential equation on your paper for the domain [-3, 3] and the range [-3, 3].
Part A: List five coordinates and the corresponding slope of their segments.
Part B: Using the slope field that you drew, describe all points in the xy-plane for which the slopes are negative.

Math
Application of derivativesSuppose the total cost C(x) (in dollars) to manufacture a quantity x of weed killer (in hundreds of liters) is given by the function C(x)= x³ - 3x² +9x +50, where x > 0.
a) Where is C(x) decreasing?
b) Where is C(x) increasing?
![Let'f be a twice-differentiable function with derivative given by f '(x) = 4x³ - 24x².
Part A: Find the x-coordinate of any possible critical points of f. Show your work.
Part B: Find the x-coordinate of any possible inflection points of f. Show your work.
Part C: Use the Second Derivative Test to determine any relative extrema and inflection points. Justify your answers.
Part D: Iff has only one critical point on the interval [5, 8], what is true about the function f on the interval [5, 8]? Justify your answers.](https://media.kunduz.com/media/sug-question/raw/77433679-1660482594.113752.jpeg?w=256)
Math
Application of derivativesLet'f be a twice-differentiable function with derivative given by f '(x) = 4x³ - 24x².
Part A: Find the x-coordinate of any possible critical points of f. Show your work.
Part B: Find the x-coordinate of any possible inflection points of f. Show your work.
Part C: Use the Second Derivative Test to determine any relative extrema and inflection points. Justify your answers.
Part D: Iff has only one critical point on the interval [5, 8], what is true about the function f on the interval [5, 8]? Justify your answers.
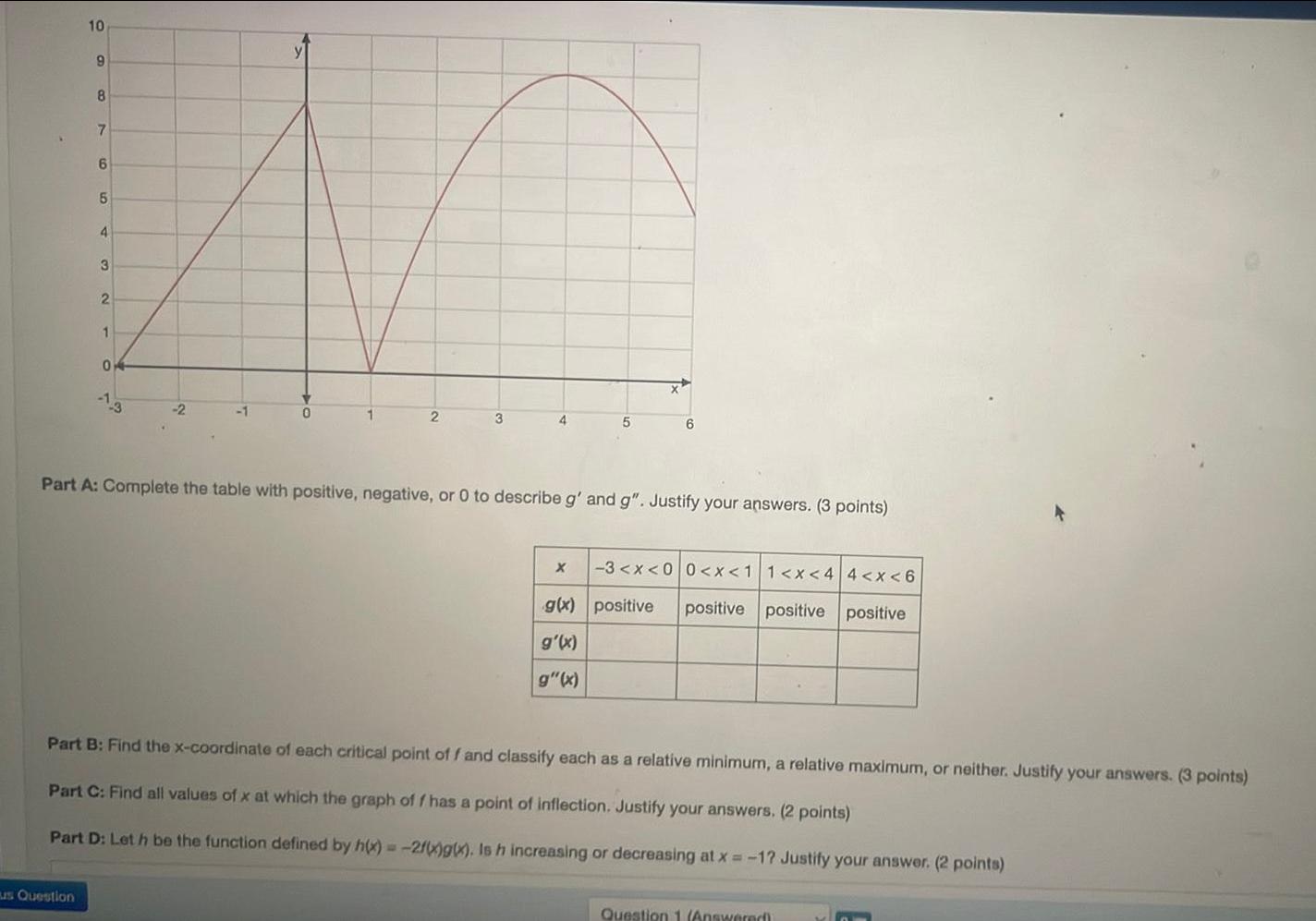
Math
Application of derivativesComplete the table with positive, negative, or 0 to describe g' and g". Justify your answers.
positive positive positive positive
Part B: Find the x-coordinate of each critical point off and classify each as a relative minimum, a relative maximum, or neither. Justify your answers.
Part C: Find all values of x at which the graph of f has a point of inflection. Justify your answers.
Part D: Let h be the function defined by h(x) = -2f(x)g(x). Is h increasing or decreasing at x=-1? Justify your answer.
![The continuous function g, consisting of two line segments and a parabola, is defined on the closed interval [-3, 6], is shown. Let f be a function such that f(-1)=- and f '(x) =](https://media.kunduz.com/media/sug-question/raw/77433638-1660481931.6741538.jpeg?w=256)
Math
Application of derivativesThe continuous function g, consisting of two line segments and a parabola, is defined on the closed interval [-3, 6], is shown. Let f be a function such that f(-1)=- and f '(x) =

Math
Application of derivativesThe height, in meters, above sea level of a NASA launched rocket is given by h(t)=-4.9t² + 151t+122
where t represents the number of seconds since the rocket was launched.
Assuming that the rocket will splash down into the ocean, after how many seconds will the splashdown
occur?
Round your answer to 3 decimal places as needed
How many meters above sea level does the rocket get at its peak?
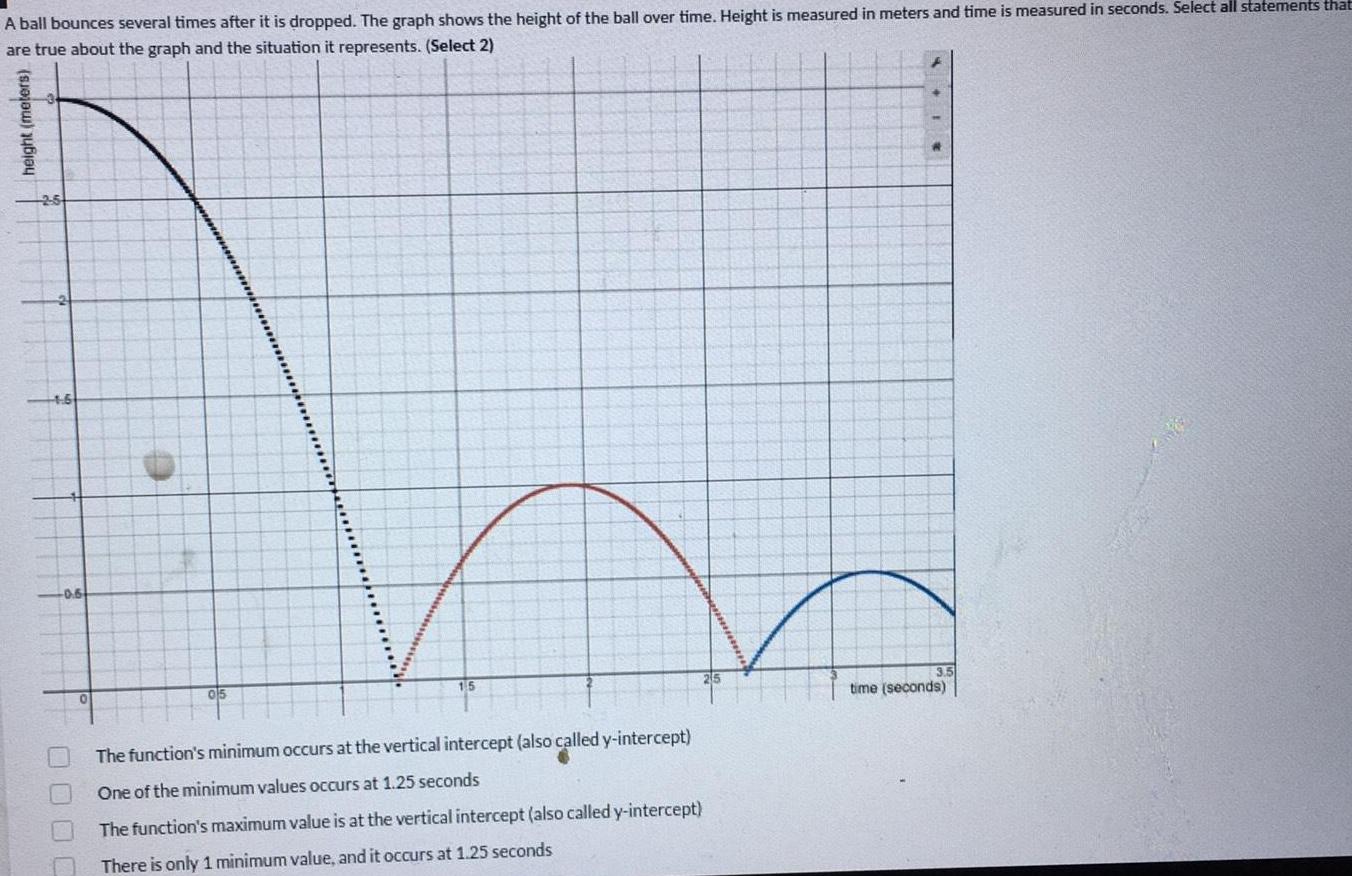
Math
Application of derivativesA ball bounces several times after it is dropped. The graph shows the height of the ball over time. Height is measured in meters and time is measured in seconds. Select all statements that are true about the graph and the situation it represents.
The function's minimum occurs at the vertical intercept (also called y-intercept)
One of the minimum values occurs at 1.25 seconds
The function's maximum value is at the vertical intercept (also called y-intercept)
There is only 1 minimum value, and it occurs at 1.25 seconds

Math
Application of derivativesConsider the function f(x) = 5x² - 10x + 1, 0≤x≤ 8.
The absolute maximum of f(x) (on the given interval) is at
x =
and the absolute maximum of f(x) (on the given interval) is
The absolute minimum of f(x) (on the given interval) is at
x=
and the absolute minimum of f(x) (on the given interval) is

Math
Application of derivativesThe radius of a circular oil spill after t minutes is given by r(t) = √4t. Find the instantaneous rate at which the radius is growing after 31 minutes.
Give your answer as a decimal approximation with at least 3 decimal places.

Math
Application of derivativesThe function A(s) that you wrote to model area is a quadratic function.
The shape that a quadratic function forms when graphed is called
a parabola.
A(x) = 100x-2x
8. Think about the possible areas of the enclosure.
a. Is there a maximum area that the enclosure can contain?
Explain your reasoning in terms of the graph and in terms
of the context.
(b. Use technology to determine the maximum of A(s).
Describe what the x- and y-coordinates of the maximum
represent in this context.
Determine the dimensions of the enclosure that will
provide the maximum area. Show your work and explain
your reasoning.
Math
Application of derivativesA particle moves along a line so that its acceleration function a(t) (in m/s²). The initial velocity v(0) = -1 (in m/s). Find the total distance (not displacement) traveled during the time period 0 ≤ t ≤ 1.

Math
Application of derivativesA company manufactures Handband, a wireless activity tracker. There are initial start-up costs involved. Additionally, the company spends a certain amount of money to manufacture each Handband. The cost of manufacturing h Handbands is given by the function, C(h) = 21h + 15000.
Which of the following statements are true? Check all that apply.

Math
Application of derivativesA ball is thrown up from the ground with an initial velocity of 80 feet per second. The height s in feet can be expressed as a function of time t in seconds by s(t) = 80t - 16t². When does the ball reach its maximum height and what is the maximum height attained?
Solve the inequality x³ - x² - 12x < 0
Solve the inequality 4/x-2≥-4/x+2
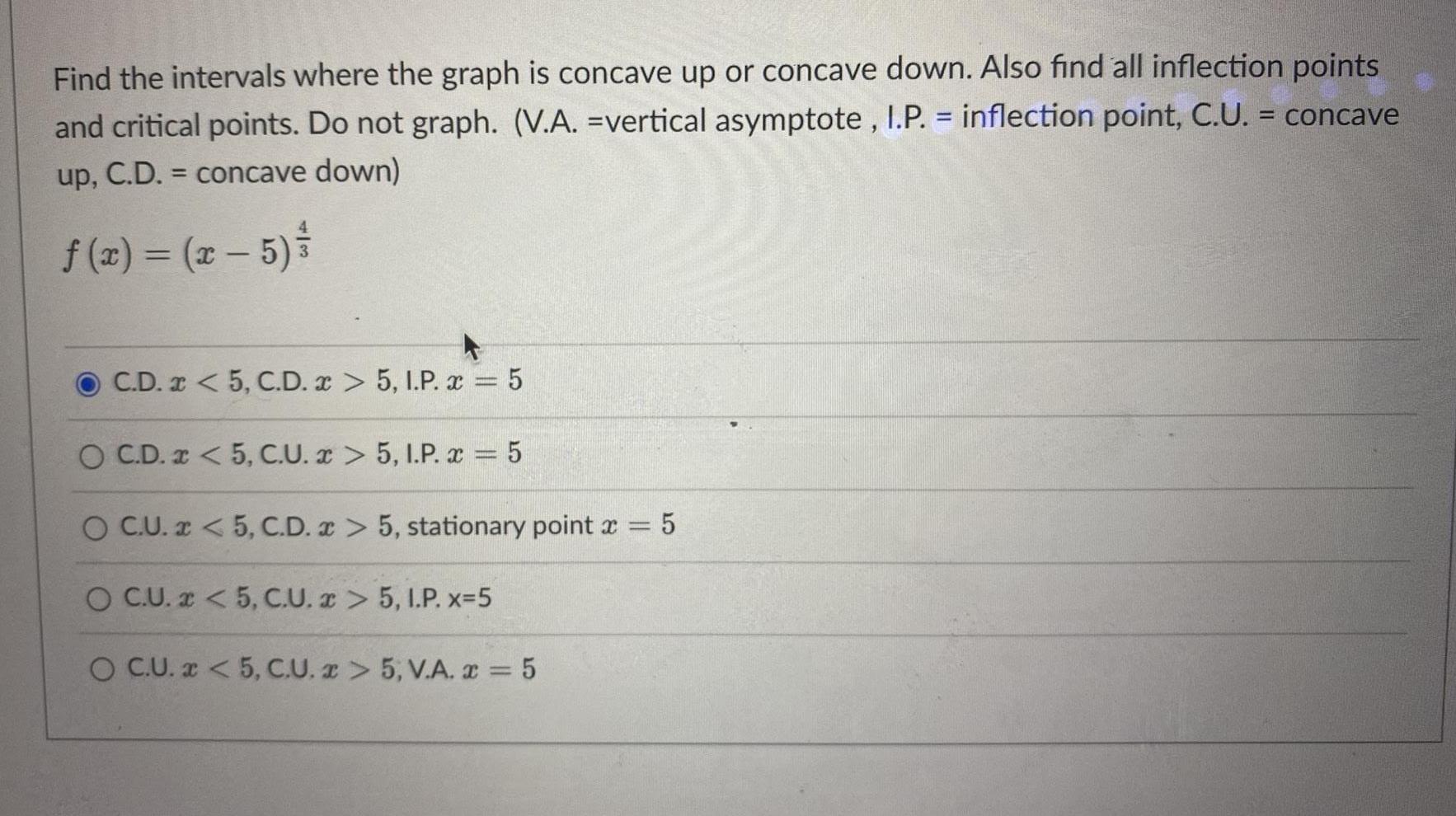
Math
Application of derivativesFind the intervals where the graph is concave up or concave down. Also find all inflection points and critical points. Do not graph. (V.A. -vertical asymptote, I.P.= inflection point, C.U. = concave up, C.D. = concave down)
f(x) = (x - 5)4/3
C.D. x < 5, C.D. x > 5, I.P. x = 5
C.D. x < 5, C.U. x > 5, I.P. x = 5
C.U. x < 5, C.D. x > 5, stationary point x = 5
C.U. x < 5, C.U. > 5, LP. x=5
C.U. x < 5, C.U. x > 5, V.A. x = 5

Math
Application of derivativesGiven g(x) (ax3+bx2+cx+d) find the values of a, b, c and d if the function passes through the points (0, 2) and ( 1, 12); and the tangent at either point is horizontal. Indicate the interval(s) on which the function is increasing or decreasing.

Math
Application of derivativesg"(x)= 2/x^2
The second derivative of the function g is given by x² Given x = 0.4 is a critical point of g, use the Second Derivative Test to determine relative extrema for g. (10 points)
g has a point of inflection at x = 0.4.
g has neither a relative minimum nor relative maximum at x = 0.4.
g has a relative maximum at x = 0.4.
g has a relative minimum at x = 0.4.

Math
Application of derivativesA store sells portable MP3 players for $100 each and, at this price, sells 120 MP3 players every month. The owner of the store wishes to increase his profit, and he estimates that, for every $2 increase in the price of MP3 players, one less MP3 player will be sold each month. If each MP3 player costs the store $70, at what price should the store sell the MP3 players to maximize profit?

Math
Application of derivativesA company's marginal cost function is MC(x) = 1/8x + 1 and its fixed costs are 100. Find the cost function. (Remember to use absolute values where appropriate.)

Math
Application of derivativesWhat is the slope of the line tangent to the graph of f(x) = 2x²e- at x = -2? Express your answer in simplest form with no negative exponents.

Math
Application of derivativesA company's revenue from selling x units of an item is given as R = 1000x - x² dollars. If sales are increasing at the rate of 80 per day, find how rapidly revenue is growing (in dollars per day) when 350 units have been sold.
$ per day
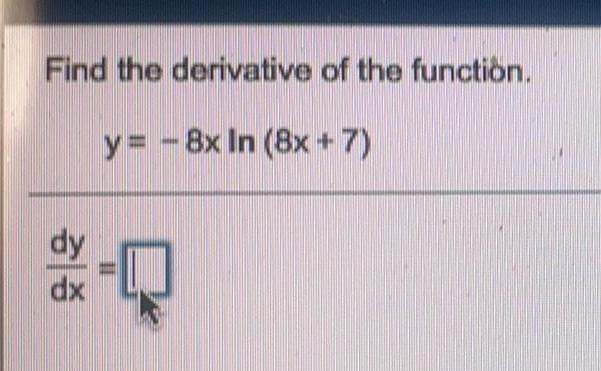

Math
Application of derivativesFind the slope of f(x) at x = -2. The graph of f(x) is shown below. Move the point on the curve to x = -2. Then plot two points on the tangent line. Finally, calculate the slope of f(x) at x = -2. Write your answer as a simplified fraction or rounded to 4 decimal places.

Math
Application of derivativesWhat are the critical numbers of the function
f(x) = x³ - 1¹7x² - 56x - 2?
Note: For answers with multiple numbers, separate using commas and enter in ascending order. Write values in decimals and round to the nearest hundredth.

Math
Application of derivativesFind dw/dt using the appropriate Chain Rule.
Function
w = x sin y
x = e^t, y = π- t
value t=0
dw/dt=
Evaluate dw/dt at the given value of t.

Math
Application of derivativesFor the function, find the points on the graph at which the tangent line is horizontal. If none exist, state that fact.
f(x) = 5x² - 2x+5
Select the correct choice below and, if necessary, fill in the answer box within your choice.
A. The point(s) at which the tangent line is horizontal is (are)
(Simplify your answer. Type an ordered pair. Use a comma to separate answers as needed.)
B. There are no points on the graph where the tangent line is horizontal.
C. The tangent line is horizontal at all points of the graph.
![Consider a function, f(x)=x²-3x,
A. determine the average rate of change in the interval [-2, 4]
B. determine the instantaneous rate of change at x = 1. You can use the small
number approximation, take h = 0.01 for example.
C. sketch the curve and the perspective tangent at x=1.](https://media.kunduz.com/media/sug-question/raw/67914857-1659098953.828596.jpeg?w=256)
Math
Application of derivativesConsider a function, f(x)=x²-3x,
A. determine the average rate of change in the interval [-2, 4]
B. determine the instantaneous rate of change at x = 1. You can use the small
number approximation, take h = 0.01 for example.
C. sketch the curve and the perspective tangent at x=1.