Algebra Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Algebra
Quadratic equations6 What are the roots of the equation x 4x 5 7x 13 0 7 What are the roots of the equation 3x315x 18x 0

Algebra
Quadratic equationsx 12x 34 9 Solve x 7x 3 0 10 What is the solution of the equation over the complex numbers x 12 0 11 Solve for x over the complex numbers x 6x 25 0

Algebra
Quadratic equations12 What is the factored form of the expression over the complex numbers 25x 16y
Algebra
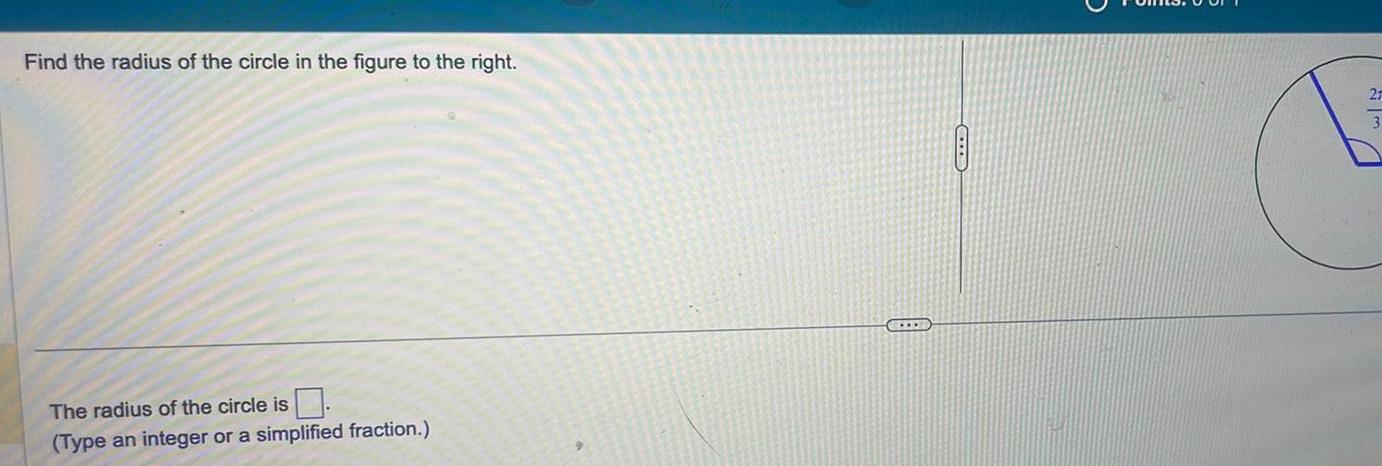
Quadratic equationsFind the radius of the circle in the figure to the right The radius of the circle is Type an integer or a simplified fraction CE 27
Algebra
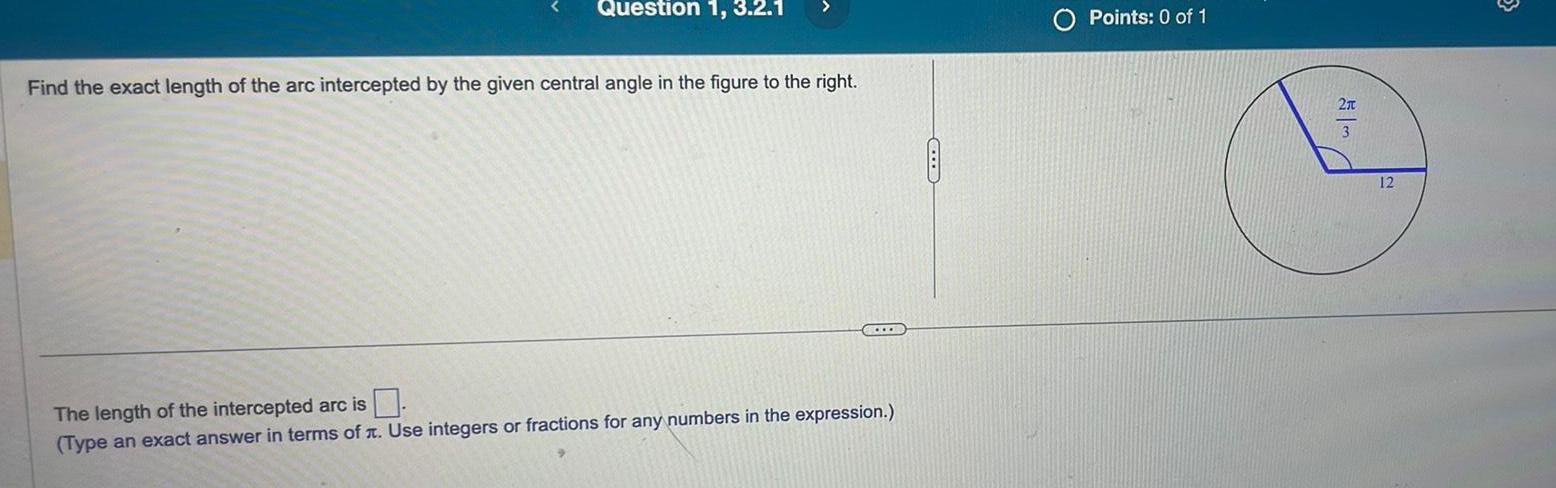
Sequences & SeriesQuestion 1 3 2 1 Find the exact length of the arc intercepted by the given central angle in the figure to the right The length of the intercepted arc is Type an exact answer in terms of Use integers or fractions for any numbers in the expression Points 0 of 1 2x 12 3
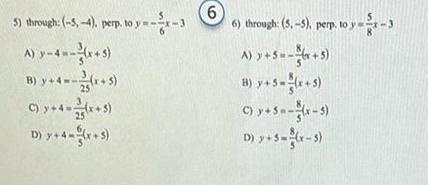
Algebra
Permutations and Combinations5 through 5 4 perp to y x A y 4 x 5 B y 4 x 5 C y 4 x 5 D y 4 x 5 6 6 through 5 5 perp to y x 3 A y 5 5 C y 5 x 3 D y 5 x 3
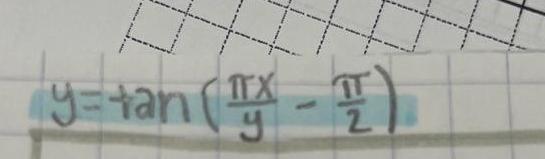


Algebra
Complex numbersThe weight of an object above the surface of the Earth varies inversely with the square of the distance from the center of the Earth Given the radius of the Earth is 3960 miles how much would a man weigh at the top of Mt Everest 5 5 miles above the surface of the Earth if he weighs 180 lbs on the surface of the Earth Round to the nearest 0 1 lb
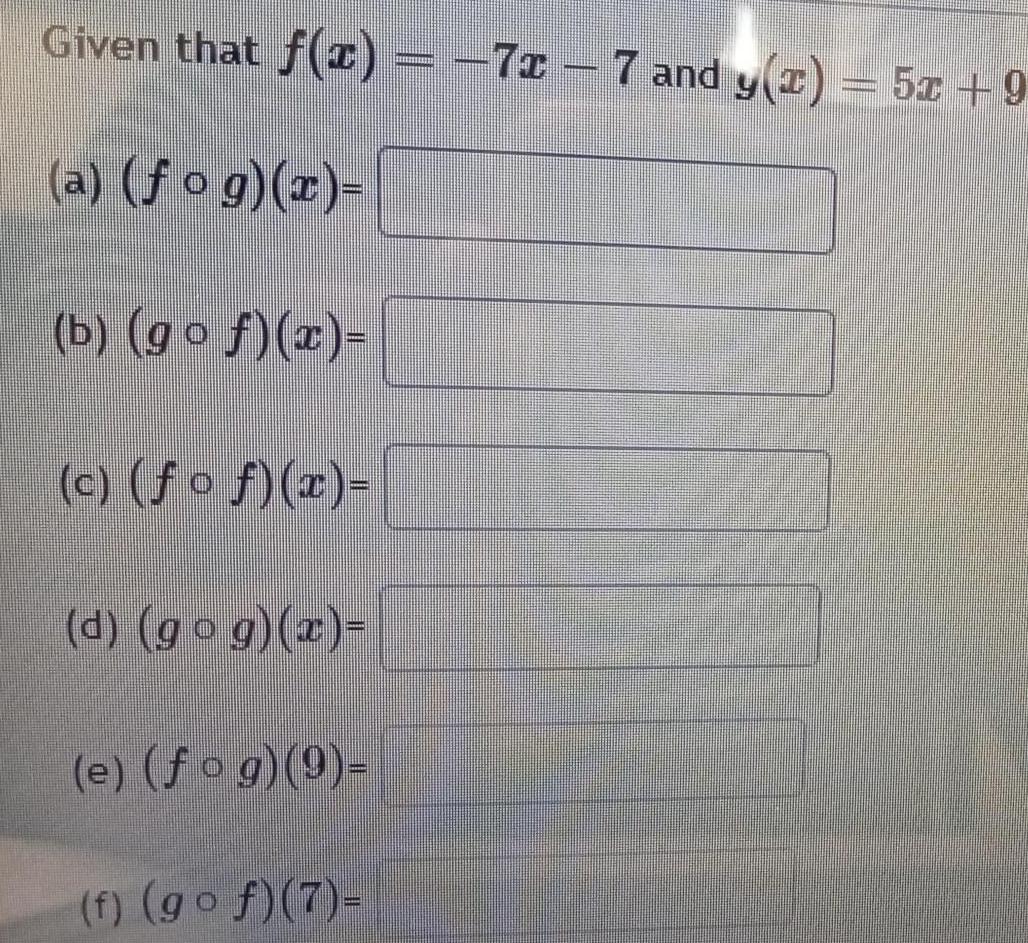
Algebra
Complex numbersGiven that f x 71 7 and y x 5x 9 www a fog x b gof x c o x d go g x e fog 9 f gof 7

Algebra
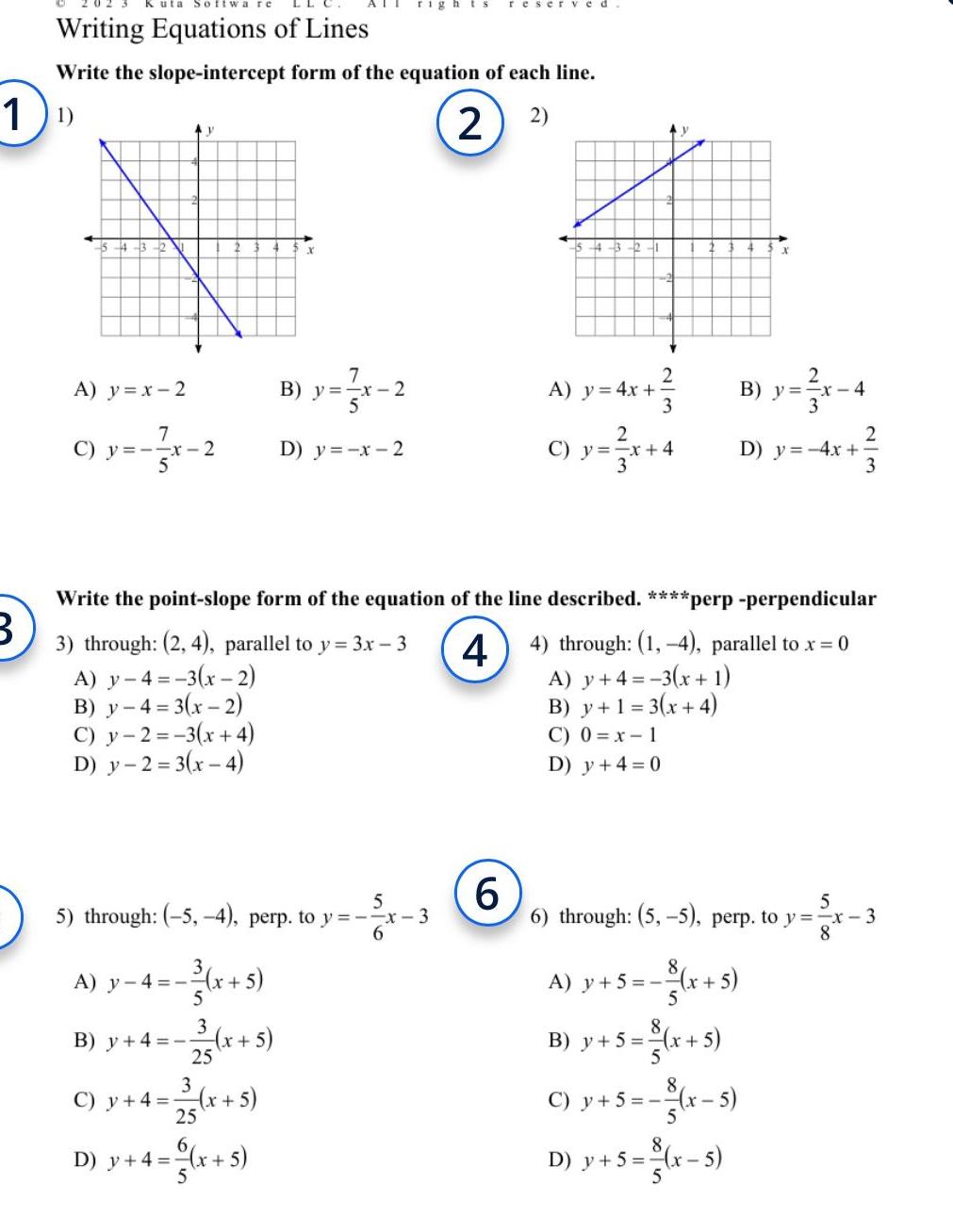
Quadratic equationsWrite the slope intercept form of the equation of the line through the given points 5 through 0 3 and 5 5 6 through 0 4 and 2 0 4 A y x 3 A y 2x 4 C y 4x 2 4 B y 3x 5 8 C y x 3 8 D y x 3 7 through 2 2 and 1 3 A y x 8 C y 8x 1 B y 5x 1 D y 5x 8 9 Slope 2 y intercept 1 A y x 2 C y 2x 2 11 Slope 2 A y 2x 2 C y 2x 2 B y 2x 1 D y 2x 2 y intercept 2 6 Write the slope intercept form of the equation of each line given the slope and y intercept 10 B y x 2 D y 2x 2 8 12 8 through 1 4 and 0 4 A y 4 C y 4x 12 Slope 10 Slope 4 y intercept 5 A y 3x 4 C y 4x 5 4 3 4 A y x 3 B y 4x 2 D y 2x 4 C y x 4 B y 2x D y 4x 3 B y 3x 4 D y 5x 4 y intercept 1 4 B y x 1 4 D y x 1 3
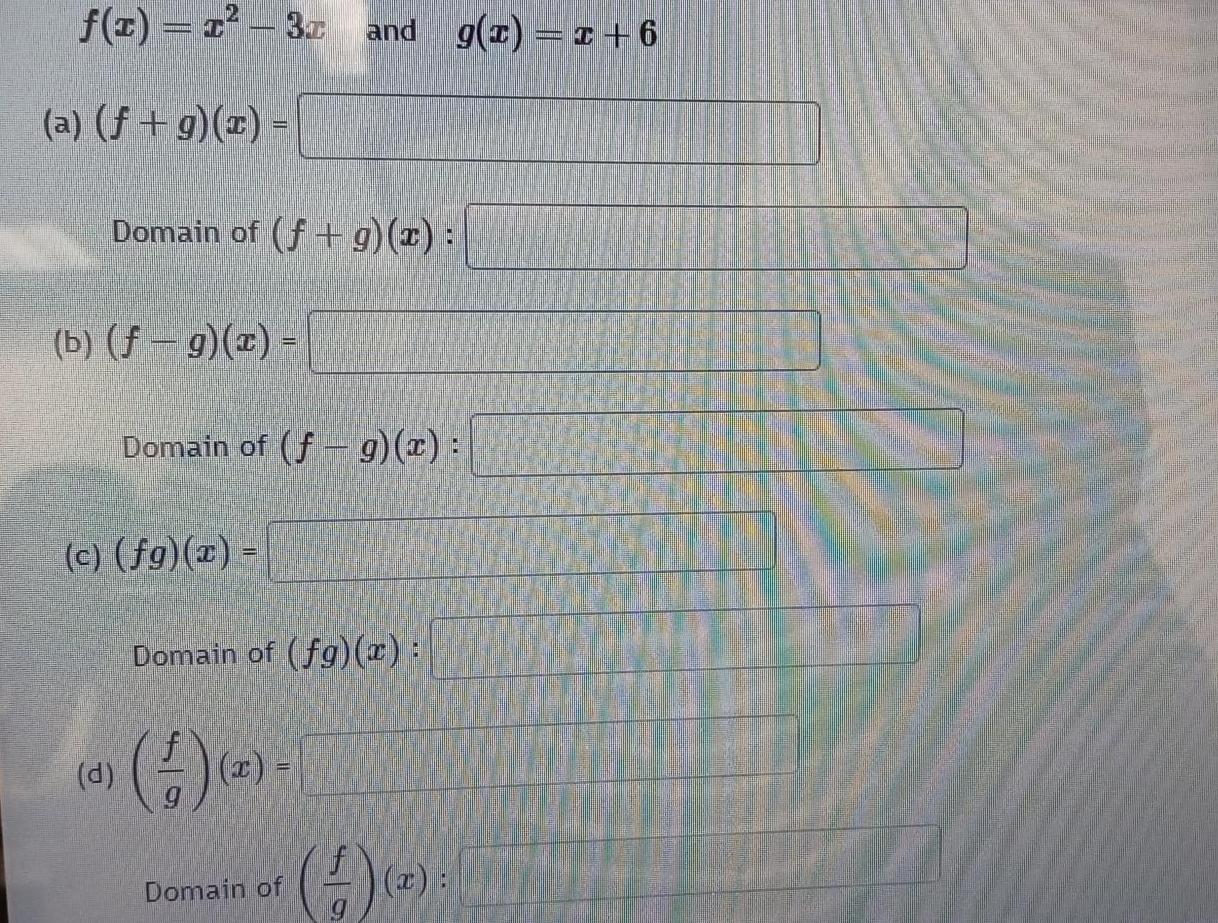
Algebra
Quadratic equationsf x x 3x and g x 1 6 a f g x Domain of f g x b f g x Domain of f g x c fg x d Domain of fg x Domain of
Algebra
Permutations and Combinations1 B Writing Equations of Lines Write the slope intercept form of the equation of each line 1 2 2 4 3 12 A y x 2 Ay 7 y x 2 C y A y 4 x x 5 5 7 B y x 2 B y 4 x 5 23 x 5 rights reserved D y x 2 5 5 through 5 4 perp to y x 3 6 C y 4 x 5 23 x 5 D y 4 x 5 4 3 2 6 A y 4x C y p x 4 Write the point slope form of the equation of the line described perp perpendicular 3 through 2 4 parallel to y 3x 3 44 through 1 4 parallel to x 0 A y 4 3 x 2 B y 4 3 x 2 A y 4 3 x 1 B y 1 3 x 4 C y 2 3 x 4 C 0 x 1 D y 2 3 x 4 D y 4 0 3 2 B y x 4 A y 5 x B y 5 5 6 through 5 5 perp to y x 3 8 x 5 x C y 5 x 5 D y 5 x 5 2 3 D y 4x x 5

Algebra
Quadratic equations7 Write the slope intercept form of the equation of the line through the given point with the give slope 8 7 through 4 5 slope 1 12 A y x 3 C y x 3 9 4x 7y 7 4 A y x 1 4 C y x 1 B y x 3 2 D y 3x 3 11 x y 1 A y 3x 1 C y x 3 5 B y x 1 7 Write the slope intercept form of the equation of each line D y x 4 B y x 1 D y x 1 7 8 through 1 3 slope A y x 12 B y x 4 4 11 1 D y C y 4 11 1 4 X 10 10 3x 5y 30 A y 6x 3 5 4 11 1 4 3 B y 6x 5 4 3 C y x 6 5 3 D y x 6 12 2x y 4 A y 4x 2 C y 4x 2 1 4 B y 2x 4 D y 2x 4

Algebra
Sequences & SeriesHow many solutions does the following system have 2x 3y 1 1 3x 2y 1 1 1 point O infinitely many solutions O two solutions

Algebra
Quadratic equationsQ2 6 points Calculate V12 numerically by using Newton Raphson and Secant methods Use initial guesses of 3 and 4 for the Secant while initial guess of 1 for Newton Raphson method Calculate until the percentage of relative approximate error becomes less than 1 Hint This can be solved by finding the root of f x x 12 Round off all your calculations to four decimal places when it is required

Algebra
Complex numbersFind the equation of the einele with center 1 2 and paring through the pofit 912 in stondend forem

Algebra
Complex numbersFind the equation of live passing through the point 210 a perpendicular to the line to the answer

Algebra
Quadratic equations317 Implus 3 1 Newton I 1 22 t S N S I Ft 34120251 HIST2 N S F m 2 2 T m L ML7
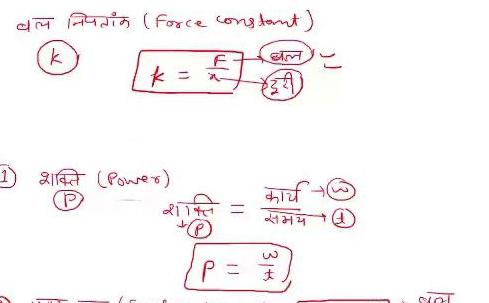

Algebra
Complex numbers230 MATHEMATICS Proof Let fand g be two functions such that d or or Rationalised 2023 24 f dx 10x dx fx 0x dx 0 Hence f x dx g x dx C where C is any real number Why f x dx fg x dx C So the families of curves f x dx C C ER and g x dx C C R are identical Hence in this sense f x dx and 120x dx dx Note The equivalence of and g x dx C C R is customarily expressed by writing f x dx g x dx without mentioning the parameter II f x g x dx ff x dx f g x dx Proof By Property 1 we have d Also On the otherhand we find that ecode f x dx f800 de dx g x dx f x g x f x g x Thus in view of Property II it follows by 1 and 2 that f f x g x dx f x dx f g x dx IV For any real number k fk f x dx k f x dx shed Rationalised 2023 24 Proof By the Property 1 f x dx k f x kaff x dx k f x dx k ffox dx INTEGRALS M www 1 2 231

Algebra
Matrices & Determinantswe know that the range of the principal value branch of sin 7 5 sin Example 2 Find the principal value of cot cot 1 2 Solution Let cot Therefore principal alue of sin 2 57 732 3 1 sin 7 sec 3 cot y 2 3 Fy Then 1 77 33 A T 11 tan 1 cos 13 If sin x y then A 0 y n cot Co 57 We know that the range of principal value branch of cot is 0 and er Find the principal values of the following 9 4 tan 3 DE OU Hence principal value of cot 10 cosec 2 Find the values of the following 1 2 2 cos 5 cos B EXERCISE 2 1 cot x 7 cot 7 3 8 cot 3 C 0 y 14 tan 3 sec 2 is equal to sin Rationalised 2023 24 TU 3 3 2 3 1 2 D 3 cosec 2 6 tan 1 9 cos B Isys1 2 TU INVERSE TRIGONOMETRIC FUNCTIONS 27 12 cos 2 3 V CORT EN T 22 2 11 12 2 sin 2 3 and 1 ublished

Algebra
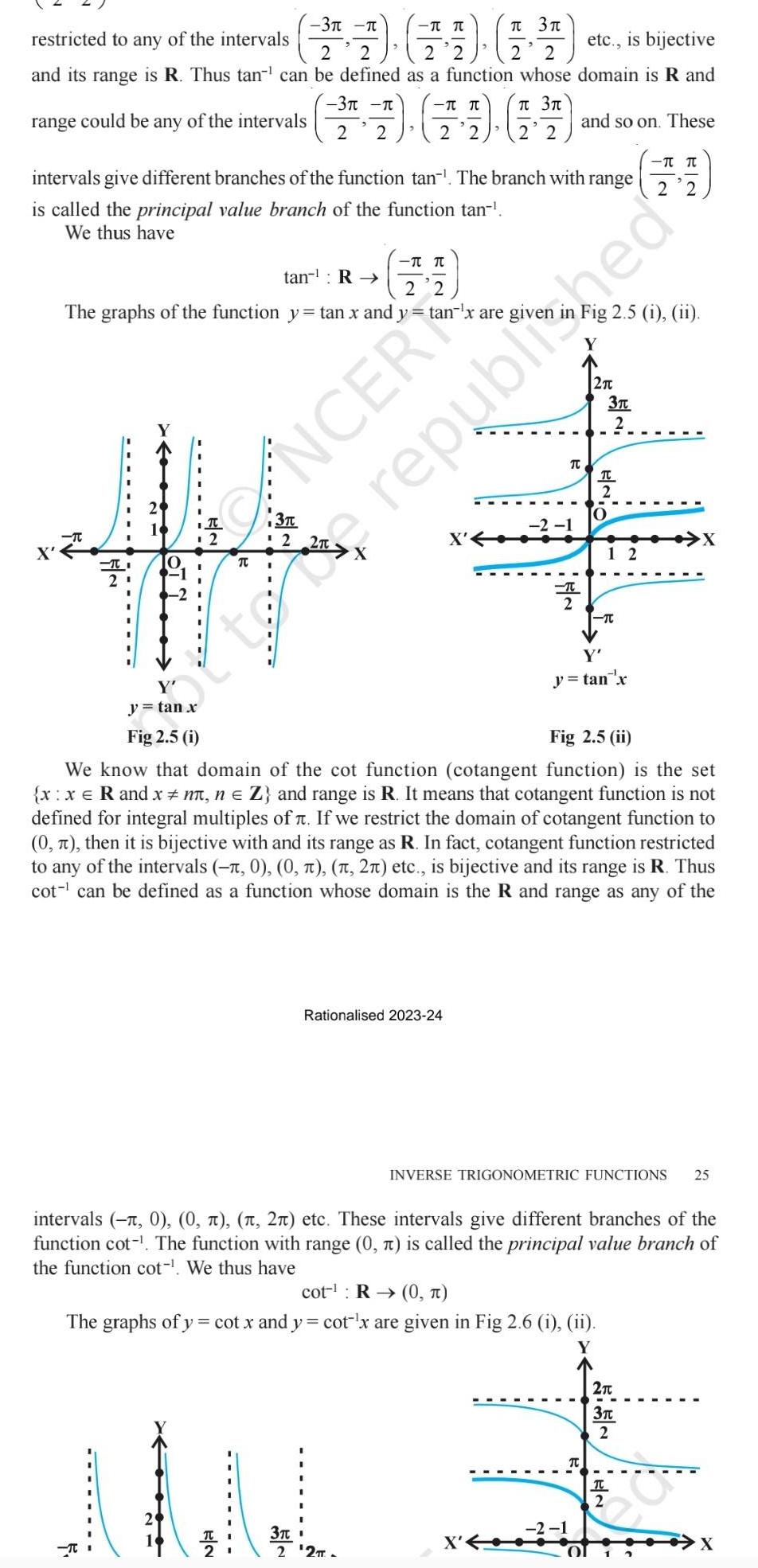
Matrices & Determinantsrestricted to any of the intervals etc is bijective 2 2 2 2 2 2 and its range is R Thus tan can be defined as a function whose domain is R and range could be any of the intervals intervals give different branches of the function tan The branch with range is called the principal value branch of the function tan We thus have tan R The graphs of the function y tan x and y tan x are given Y y tan x intervals T 2 3 3 17 19 4 2 2 2 2 2 2 T T T 3 2 NCER X Rationalised 2023 24 and so on These 2 1 TC T Fig 2 5 i ii 2 3T 2 T 2 O 12 TC 2 2 Y y tan x republished Fig 2 5 i Fig 2 5 ii We know that domain of the cot function cotangent function is the set x x R and x n n Z and range is R It means that cotangent function is not defined for integral multiples of If we restrict the domain of cotangent function to 0 then it is bijective with and its range as R In fact cotangent function restricted to any of the intervals 0 0 2 etc is bijective and its range is R Thus cot can be defined as a function whose domain is the R and range as any of the X INVERSE TRIGONOMETRIC FUNCTIONS 25 2 ete These intervals give different branches of the

Algebra
Matrices & Determinants90 70 75 Suppose Fatima wants to know the total production of sport shoes in each price category Then the total production In category 1 for boys 80 90 for girls 60 50 In category 2 for boys 75 70 for girls 65 55 In category 3 for boys 90 75 for girls 85 75 80 90 This can be represented in the matrix form as 75 70 90 75 1 2 3 44 MATHEMATICS 80 75 90 60 65 85 911 912 913 Thus if A 921 922 923 1 2 3 Rationalised 2023 24 Example 6 Given A This new matrix is the sum of the above two matrices We observe that the sum of two matrices is a matrix obtained by adding the corresponding elements of the given matrices Furthermore the two matrices have to be of the same order 2x3 matrix Then we define A B is a 2 3 matrix and B 31 2 3 0 a b a 2 b 2 a21 b 1 a22 b 2 and B 50 55 75 2 5 60 50 65 55 85 75 2 3 In general if A a and B b are two matrices of the same order say m n Then the sum of the two matrices A and B is defined as a matrix C c c a b for all possible values of i and j where b b2 b13 b21 b2 a 3 b 3 a23 b 3 b23 is another 45 Since A B are of the same order 3 Therefore addition of A and B is defined and is given by 12 55 1 255 1 1 2 6 1 1 5 07

Algebra
Matrices & DeterminantsSupport Fatiila has two latiunits at places A allu D Each factory products spont shoes for boys and girls in three different price categories labelled 1 2 and 3 The quantities produced by each factory are represented as matrices given below 44 Boys 80 75 90 Suppose Fatima wants to know the total production of sport shoes in each price category Then the total production In category 1 for boys 80 90 for girls 60 50 In category 2 for boys 75 70 for girls 65 55 In category 3 for boys 90 75 for girls 85 75 80 90 This can be represented in the matrix form as 75 70 90 75 1 2 3 MATHEMATICS Factory at A In general if A 2x3 matrix Then we define A B Girls 60 65 85 Example 6 Given A A B 9 1 912 913 Thus if A is a 2 x 3 matrix and B 921 922 923 This new matrix is the sum of the above two matrices We observe that the sum of two matrices is a matrix obtained by adding the corresponding elements of the given matrices Furthermore the two matrices have to be of the same order Rationalised 2023 24 2 2 31 Since A B are of the same order and is given by 1 2 3 2 3 0 2 3 1 5 1 1 1 5 1 1 3 3 0 Factory at B Boys 90 70 75 Then the sum of the two matrices A and B is defined as a matrix C c a b for all possible values of i and j a and B b are two matrices of the same order say m n where defined For example if A a b a 2 b 2 a21 b 1 a22 b22 and B 2 5 1 2 3 B 1 0 2 3 Girls 50 55 75 60 50 65 55 85 75 2 3 1 5 0 1 0 2 6 b b 2 b13 b 1 b22 b 3 a 3 b 3 a23 b 3 1 2 3 1 10 1 Therefore addition of A and B is defined is another Note 1 We emphasise that if A and B are not of the same order then A B is not use then A B is not defined

Algebra
Matrices & Determinantssin We know that the range of the principal value branch of sin is 1 1 TU 4 cot Example 2 Find the principal value of cot Solution Let cot y Then 3 Therefore principal value of sin 1 sin meno 7 sec cot y Find the principal values of the following 1 2 cot 3 3 We know that the range of principal value branch of cot is 0 and 2 1 Hence principal value of cot 9 4 tan 3 2 3 A T 11 tan 1 cos 13 If sin x y then A 0 y n cot 1 2 10 cosec 2 Find the values of the following 2 cos 5 cos EXERCISE 2 1 B Cop sin C 0 y n 14 tan 3 sec 2 is equal to cot 8 cot 3 3 3 2 er 2 Rationalised 2023 24 11 12 D EN IS IS 3 cosec 2 6 tan 1 2 3 INVERSE TRIGONOMETRIC FUNCTIONS 27 9 cos T B 1 120 2 T 12 cos CERT p I 1 2 2 11 2 2 sin 11 2 w 5 and 2 ublished 2 3 Properties of Inverse Trigonometric Functions In this section we shall prove some important properties of inverse trigonometric functions It may be mentioned here that these results are valid within the principal

Algebra
Complex numbers1 Example 4 Express tan Solution We write ii Take x cos 0 then proceeding as above we get sin tan COS X 1 sin x Example 5 Write cot Therefore cot 3 tan tan tan tan 1 X 1 x 1 1 COS X Solution Let x sec 0 then x 1 1 N sin 2sine cose sin Sin20 20 2 sin x X X X sin COS sin COMME 17 2 2 2 X x COS sin 2 3 X COS sin 2 X COS sin 2 Prove the following 1 3sin x sin 3x 4x xe X 0 T X tan 4 2 X X X sin 2 sin cos 2 2 2 sin 2 3cos x cos 4x 3x XE X 2 X 2 tan T X 4 2 Rationalised 2023 24 le of you 1 sec 0 Write the following functions in the simplest form 1 x 1 x 1 in the simplest form EXERCISE 2 2 in the simplest form 1 tan INVERSE TRIGONOMETRIC FUNCTIONS 29 1 tan cot cot 0 0 sec x which is the simplest form 0 1 tan 0 X 1 x 2 cos x NORT COS X 1 cos x ublished 0 x T

Algebra
Quadratic equationsGiven F 0 cos x 0 C y 2 4 y 0 z 0 0 x T which of the following is a normal vector of cylinder C O 0 cos u 0 O None of the statements are normal to the cylinder O 2 cos u u 2 sin u O 0 2 cos u 2 sin u fa 2 coc 2 sin 2ul

Algebra
Complex numberstrigonometric functions In fact they will be valid only for some values of x for which inverse trigonometric functions are defined We will not go into the details of these values of x in the domain as this discussion goes beyond the scope of this textbook Let us recall that sin x then x sin y and if x sin y then y sin x This is equivalent to For suitable values of domain similar results follow for remaining trigonometric functions 28 sin sin x x x 1 1 and sin sin x x x E 2 MATHEMATICS We now consider some examples Example 3 Show that 1 sin 2x 1 x 2 sin X 1 ii sin 2x 1 x 2 cos x Solution tan Rationalised 2023 24 i Let x sin 0 Then sinx 0 We have 1 Example 4 Express tan Solution We write 25x5 1 2 x 2 sin 2x 1 x sin 2 sin 0 1 sin 0 COS X 1 sinx ii Take x cos 0 then proceeding as above we get sin tan x 1 not sin 2sine cos0 sin sin2 2 sin x 2 COS 2 2 X 2 X 2 sin COS X 2 2 X X cos sin COS sin 2 x 2 sin the simplest form t to be reputasted x 2 cos x
Algebra
Complex numbersrestricted to any of the intervals 1 1 14 etc is bijective 2 2 2 2 2 and its range is R Thus tan can be defined as a function whose domain is R and 3 3 range could be any of the intervals 2 2 2 2 T intervals give different branches of the function tan The branch with range is called the principal value branch of the function tan We thus have tan R The graphs of the function y tan x and ytan x are giver 2 y tan x Fig 2 5 i T T 3 CANCER T TT 2 2 3 2 TI 21 T Rationalised 2023 24 3 t 2 2TT 2 1 T 2 and so on These 74 2 2 Fig 2 5 i ii Y 2 2 1 Fig 2 5 ii We know that domain of the cot function cotangent function is the set x x R and x n n Z and range is R It means that cotangent function is not defined for integral multiples of If we restrict the domain of cotangent function to 0 then it is bijective with and its range as R In fact cotangent function restricted to any of the intervals 0 0 2 etc is bijective and its range is R Thus cot can be defined as a function whose domain is the R and range as any of the cot R 0 The graphs of y cot x and y cot x are given in Fig 2 6 i ii 3T 2 TC 2 O Y y tan x T intervals 1 0 0 2 etc These intervals give different branches of the function cot The function with range 0 is called the principal value branch of the function cot We thus have 12 INVERSE TRIGONOMETRIC FUNCTIONS 25 republished T 2T 3 2 X

Algebra
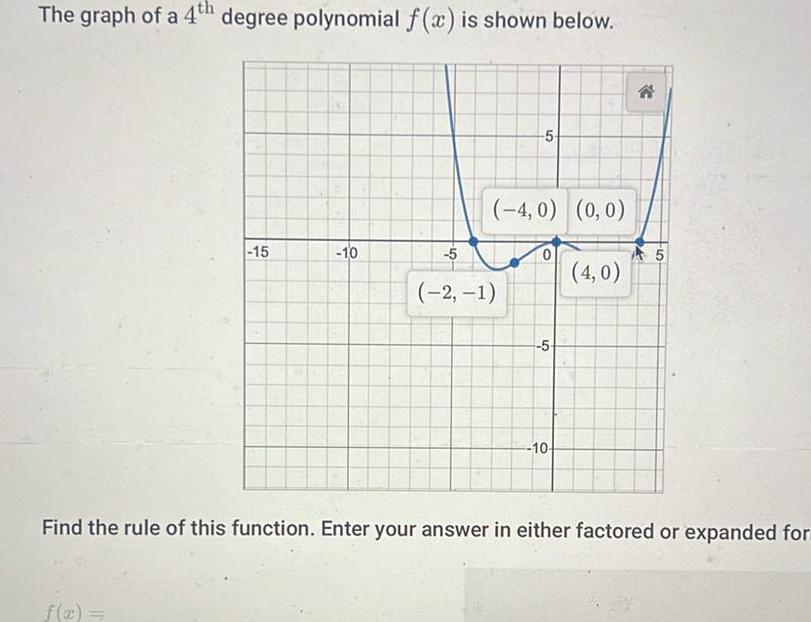
Quadratic equationsThe graph of a 4th degree polynomial f x is shown below 15 f x 10 5 4 0 0 0 4 0 5 2 1 5 10 C 5 Find the rule of this function Enter your answer in either factored or expanded for
Algebra
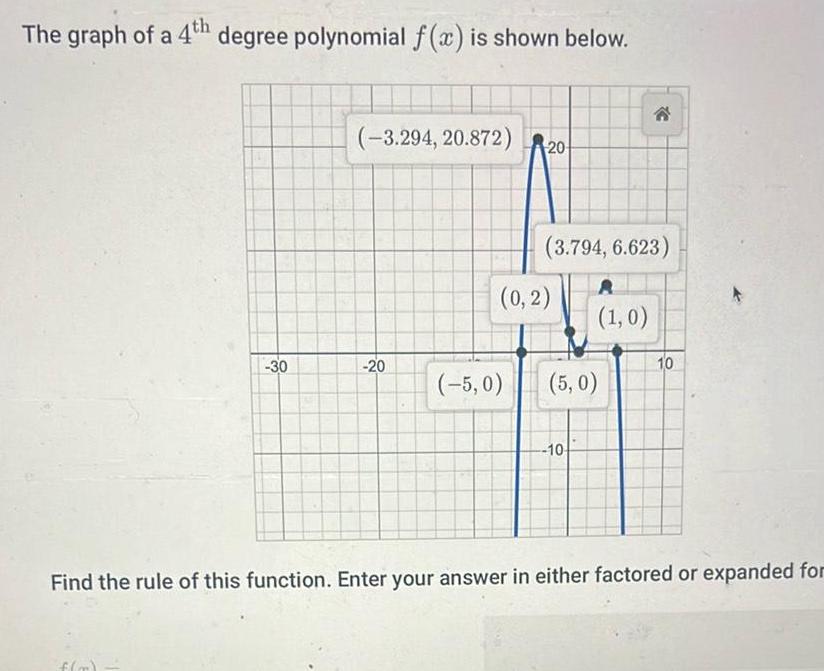
Quadratic equationsThe graph of a 4th degree polynomial f x is shown below 30 3 294 20 872 20 20 3 794 6 623 0 2 1 0 5 0 5 0 10 10 Find the rule of this function Enter your answer in either factored or expanded for
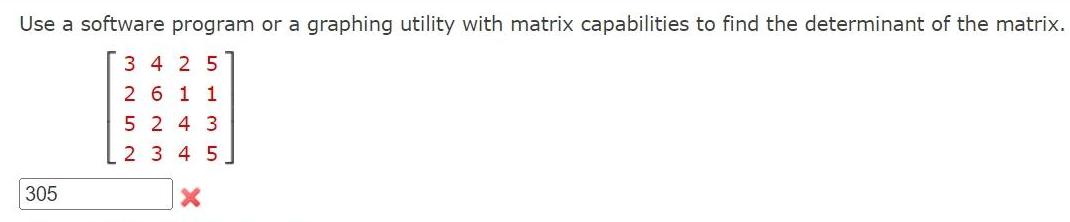
Algebra
Matrices & DeterminantsUse a software program or a graphing utility with matrix capabilities to find the determinant of the matrix 34 25 26 11 305 5243 2 3 4 5 X

Algebra
Quadratic equations9 Use the converse of the Pythagorean theorem to show that the vertices 2 1 4 0 and 5 7 form a right triangle Compute the area of the triangle

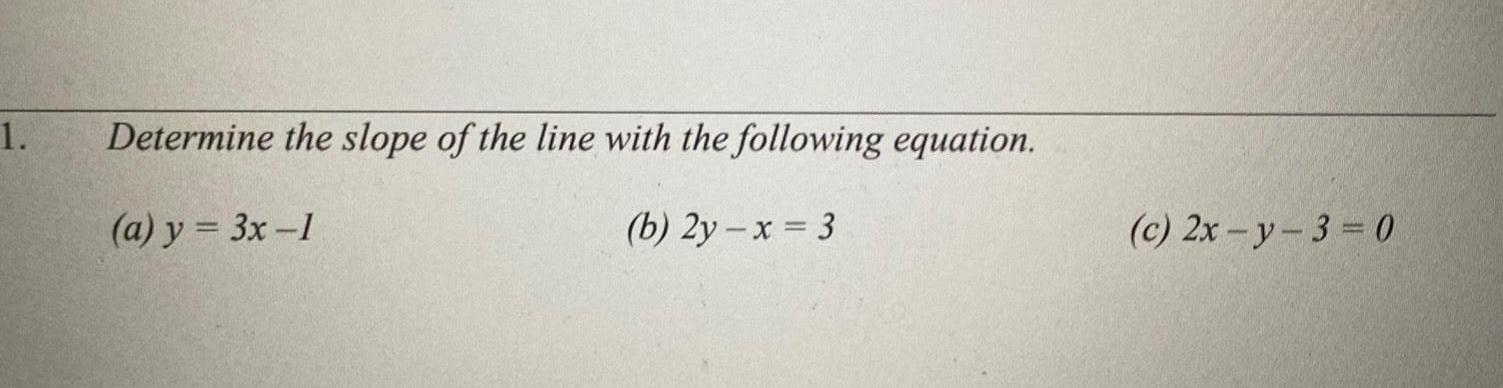
Algebra
Permutations and Combinations1 Determine the slope of the line with the following equation a y 3x 1 b 2y x 3 c 2x y 3 0
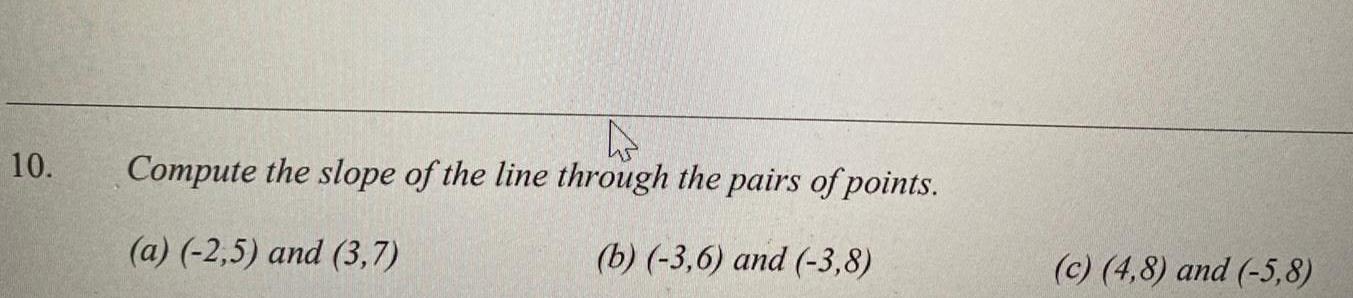
Algebra
Complex numbers10 4 Compute the slope of the line through the pairs of points a 2 5 and 3 7 b 3 6 and 3 8 c 4 8 and 5 8


Algebra
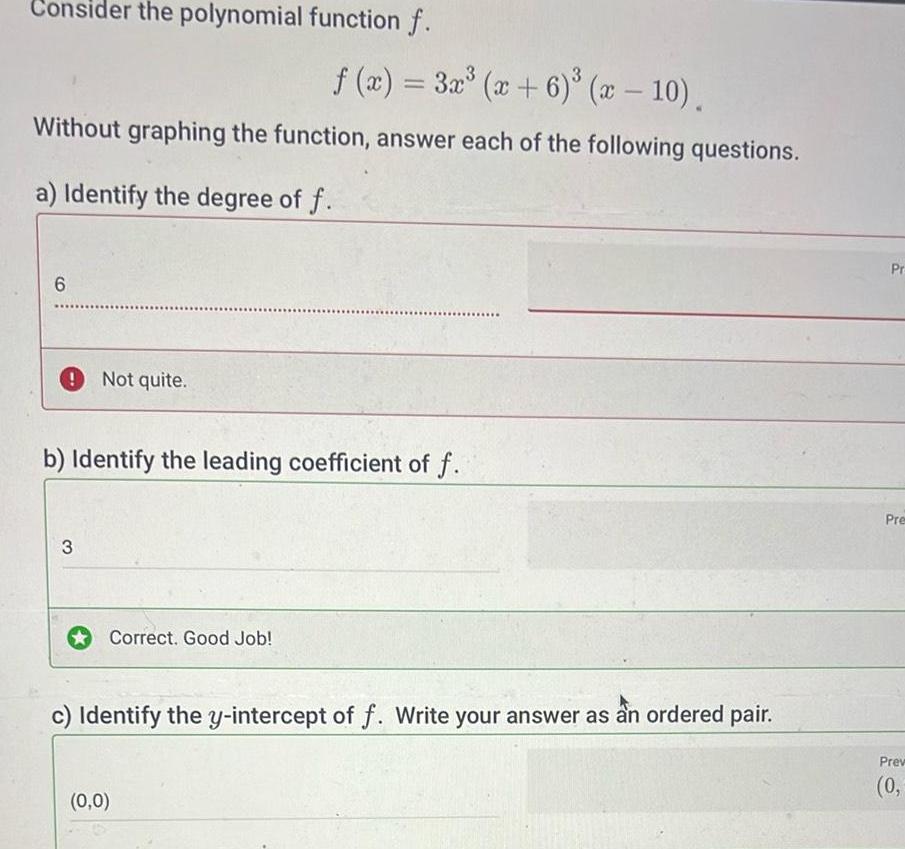
Complex numbersConsider the polynomial function f f x 3x x 6 x 10 Without graphing the function answer each of the following questions a Identify the degree of f 6 Not quite b Identify the leading coefficient of f 3 Correct Good Job c Identify the y intercept of f Write your answer as an ordered pair 0 0 Pr Pre Prev 0



Algebra
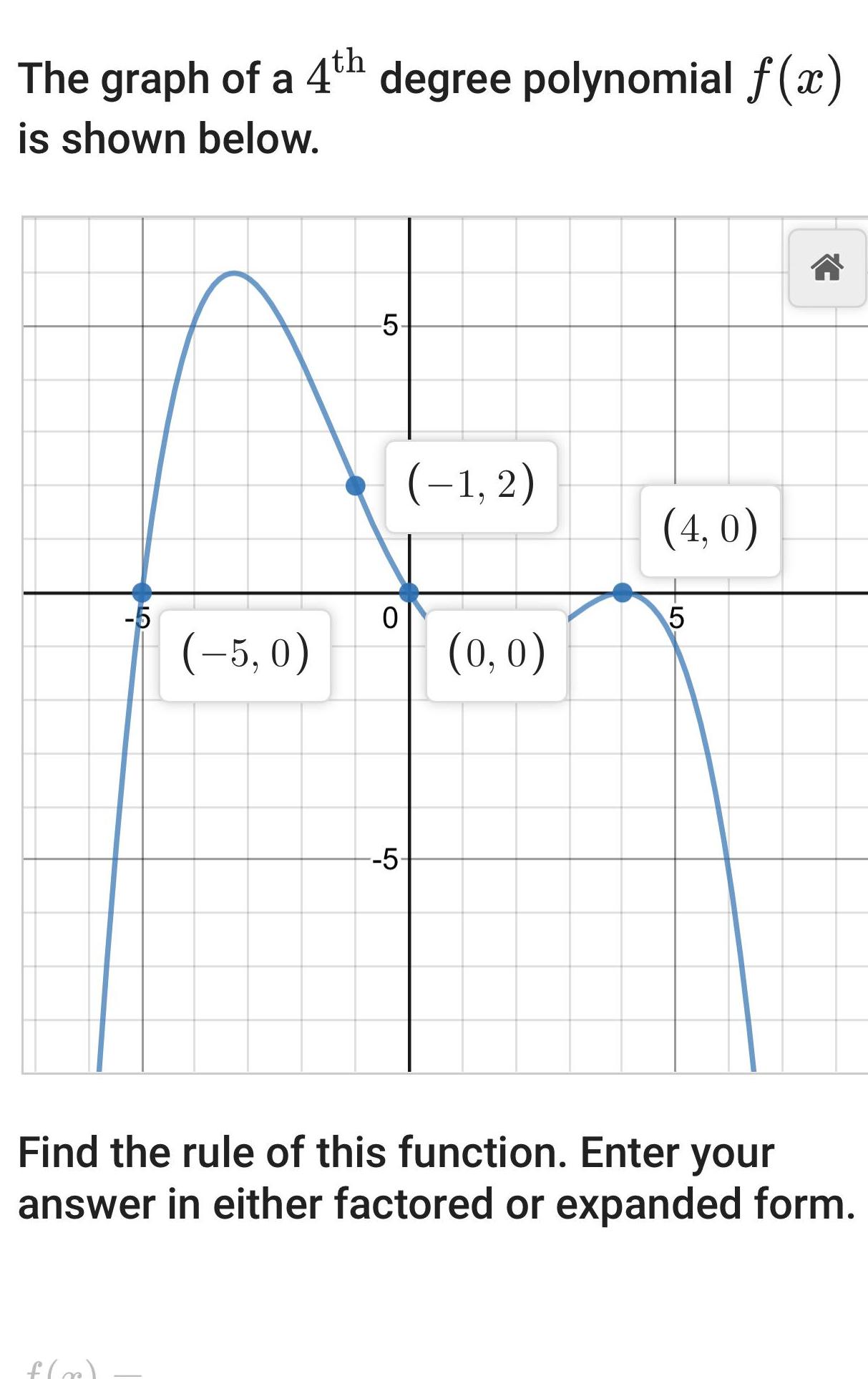
Quadratic equationsThe graph of a 4th degree polynomial f x is shown below LO f x 5 0 LO 0 1 2 5 0 0 4 0 5 Find the rule of this function Enter your answer in either factored or expanded form

Algebra
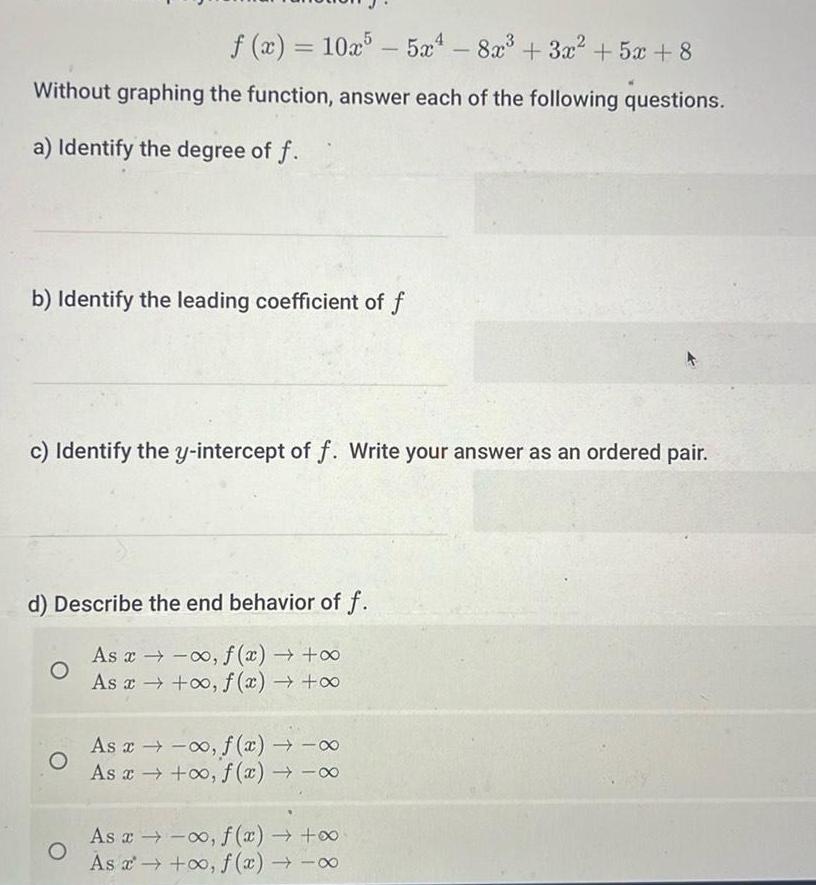
Quadratic equationsf x 10x55x4 8x 3x 5x 8 Without graphing the function answer each of the following questions a Identify the degree of f b Identify the leading coefficient of f c Identify the y intercept of f Write your answer as an ordered pair d Describe the end behavior of f As x f x As x o f x O O As x f x As x o f x As x f x As f x

