Permutations and Combinations Questions and Answers

Algebra
Permutations and CombinationsExercise 8 5 2 Use the fact that A A 1 I and Proposition 8 2 8 to solve for det A in terms of det

Algebra
Permutations and CombinationsTry It In a basketball game Mike makes 60 of his shots If he makes 12 baskets how many shots did he take p 72

Algebra
Permutations and Combinations3 Calculate the requested measures in parts a through f for bonds A and B assume that each bond pays interest semiannually Coupon Yield to maturity Maturity years Par Price Bond A Bond B 9 8 8 8 2 5 1000 00 1000 00 1000 00 1004 055 a What is the price value of a basis point for bonds A and B b Compute the Macaulay durations for the two bonds c Compute the modified duration for the two bonds d Compute the approximate duration for bonds A and B using the shortcut formula by changing yields by 20 basis points and compare your answers with those calculated in part c e Compute the convexity measure for both bonds A and B f Compute the approximate convexity measure for bonds A and B using the shortcut formula by changing yields by 20 basis points and compare your answers to the convexity measure calculated in part e
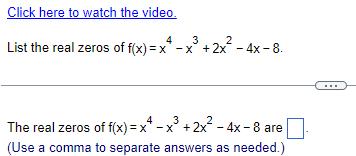
Algebra
Permutations and CombinationsClick here to watch the video 4 3 List the real zeros of f x x x 2x 4x 8 4 3 2 The real zeros of f x x x 2x 4x 8 are Use a comma to separate answers as needed
Algebra
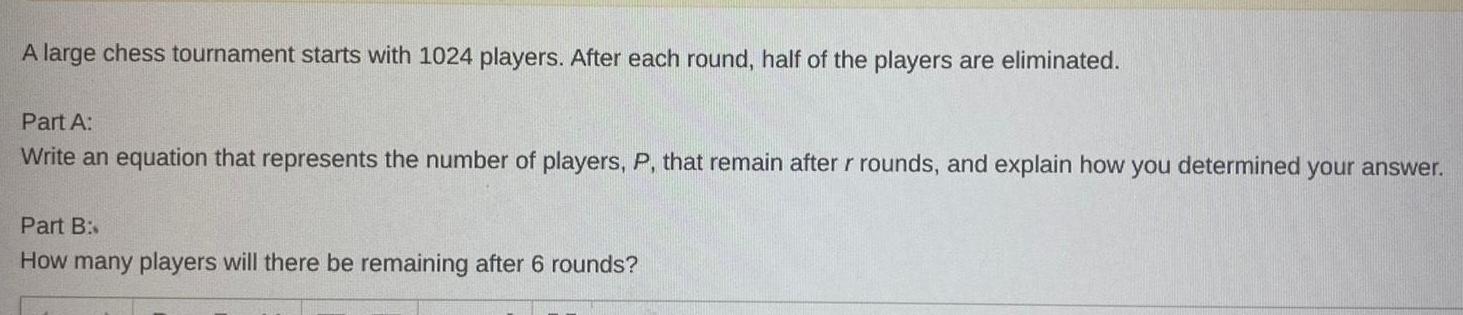
Permutations and CombinationsA large chess tournament starts with 1024 players After each round half of the players are eliminated Part A Write an equation that represents the number of players P that remain after r rounds and explain how you determined your answer Part B How many players will there be remaining after 6 rounds

Algebra
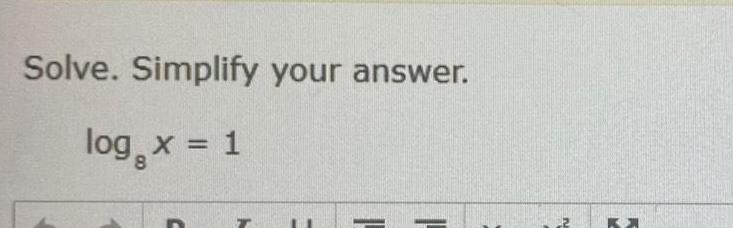
Permutations and CombinationsWhich of these represents the value of log 200 rounded to the nearest hundredt A B C D 2 30 3 29 20 00 40 00

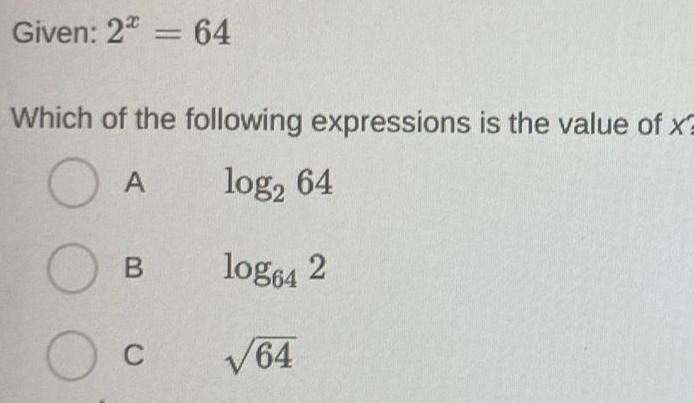
Algebra
Permutations and CombinationsGiven 2 64 Which of the following expressions is the value of x O A log 64 log64 2 64 O O C B
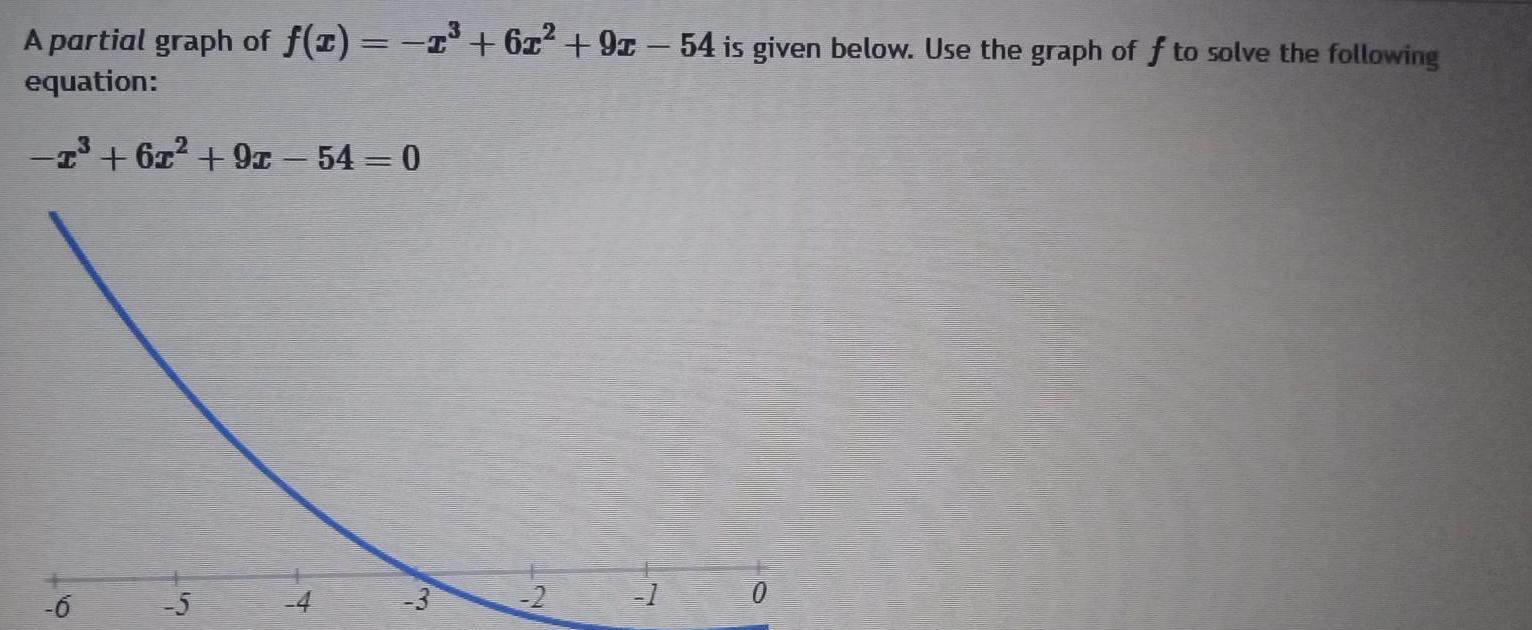
Algebra
Permutations and Combinationspartial graph of f x 1 67 92 54 is given below Use the graph of f to solve the following equation 1 6x 91 54 0 6 5 4 3 2 1 0

Algebra
Permutations and CombinationsSolve the following polynomial equation given 96x 104x 160x 150 0 5 3 is a root of f x 96r 104r 160 150 4

Algebra
Permutations and CombinationsSolve the following polynomial equation given 1 is a root of f x 302 24 30z 24 30r 24z 30z 24 0

Algebra
Permutations and Combinations3 Solve the following polynomial equation given 1 is a root of f x x 8x 1lz 20 z 87 11z 20 0
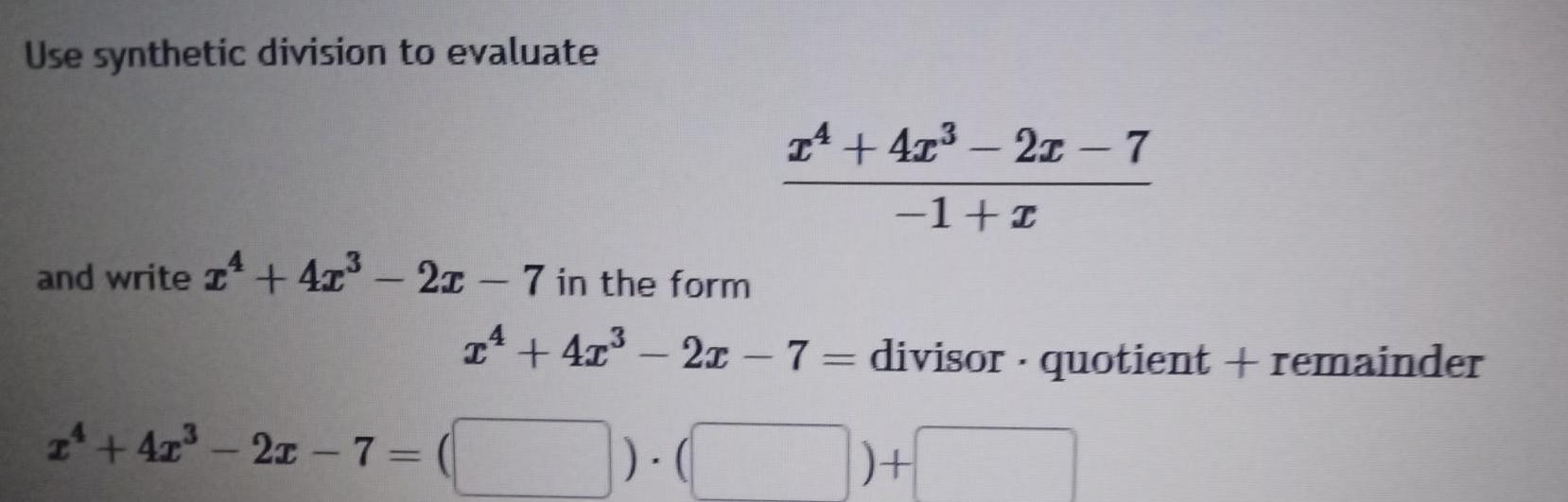
Algebra
Permutations and CombinationsUse synthetic division to evaluate and write 4x 2r 7 in the form 1 41 21 7 T 41 2x 7 1 r 4x 2x 7 divisor quotient remainder

Algebra
Permutations and CombinationsUse synthetic division to evaluate and write 1 36x 36 in the form T T 36x 36 divisor quotient remainder h Use the above result to determine the remaining roots of x r 36x 36 List all roots using a comma separated list 1 1 36x 36 are 2 2 362 36 2 6 The roots of 2 2 36x 36 a

Algebra
Permutations and CombinationsUse polynomial long division to evaluate and write the solution in form 6x x 7 T 6x x7 x 1 quotient remainder divisor
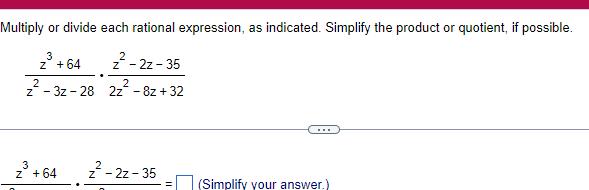
Algebra
Permutations and CombinationsMultiply or divide each rational expression as indicated Simplify the product or quotient if possible 3 z 64 2 z3z 28 3 Z 64 z 2z 35 2 2z 8z 32 z 2z 35 Simplify your answer
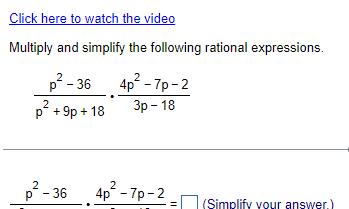
Algebra
Permutations and CombinationsClick here to watch the video Multiply and simplify the following rational expressions p 36 2 p 9p 18 2 p 36 4p 7p 2 3p 18 2 4p 7p 2 Simplify your answer
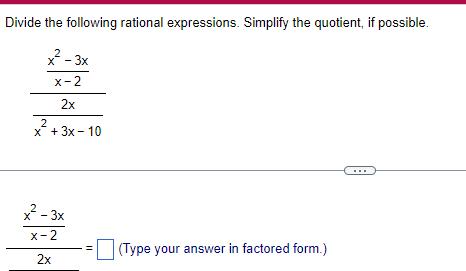
Algebra
Permutations and CombinationsDivide the following rational expressions Simplify the quotient if possible 2 x 3x x 2 2x 2 x 3x 10 2 x 3x X 2 2x Type your answer in factored form
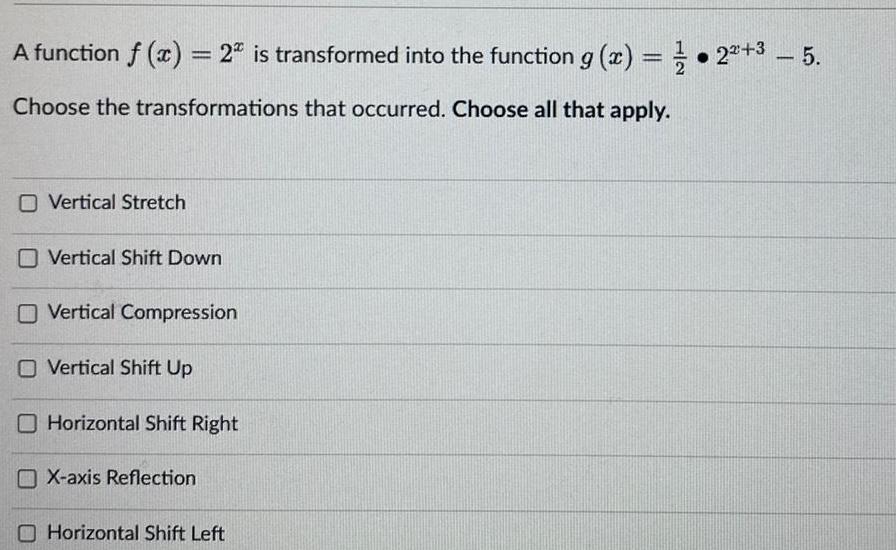
Algebra
Permutations and CombinationsA function f x 2 is transformed into the function g x 2 5 Choose the transformations that occurred Choose all that apply O Vertical Stretch Vertical Shift Down Vertical Compression O Vertical Shift Up Horizontal Shift Right X axis Reflection Horizontal Shift Left
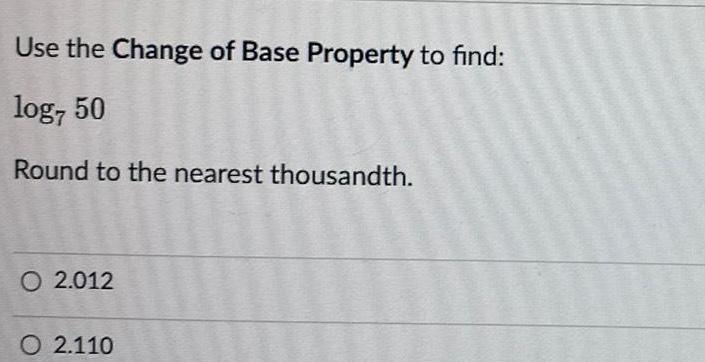
Algebra
Permutations and CombinationsUse the Change of Base Property to find log7 50 Round to the nearest thousandth O 2 012 O 2 110
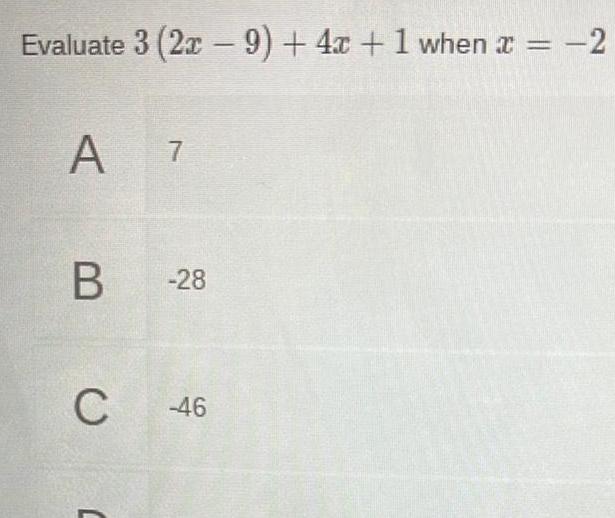

Algebra
Permutations and CombinationsB4 Identity Laws XVO x XAI x B5 Complementation Laws x X 0 x V x I We write this algebraic structure as B X V A 0 1 or simply B if the context makes the meaning of tlie other terms clear The two operations V and A are called the join operation and meet operation respectively The unary operation is called the complementation From our discussion preceding the definition above you would agree that the set S of propositions is a Booleaii algebra where T and F will do the job of I and O respectively Thus S A V F T is an example of a Boolean algebra We give another example of a Boolean algebra below Example 1 Let X be a non empty set and P X denote its power set i e P X is the set consisting of all the subsets of the set X Show that P X is a Boolean algebra Solution We take the usual set theoretic operations of intersection n union u and complementation in P X as the three required operations Let and X play the roles of O and I respectively Then from MTE 04 you can verify that all the coriditions for P X U n X to be a Boolean algebra hold good For instance the identity laws B4 follow from two set theoretic facts hamely the intersection of any subset with the whole set is the set itself arid the union of any set with the empty set is the set itself On the otlier hand the complementation laws B5 follow from another set of facts from set theory namely the intersection of any subset with its complement is the empty set and the union of any set with its complement is the whole set Yet another example of a Boolean algebra is based on switching circuits For this we first need to elaborate on the functioning of ordinary switches in a mathematical way In fact we will present the basic ides which helped tlic American C E Shannon to detect tlic connection between the functioning of switches and Boole s symbolic logic You may be aware of the functioning of a simple on off switch which is commonly used as an essential component in the electric or electronic networking systems A switch is a clevice which allows the current to flow only when it is placed in tlic ON position i e when the gap is closed by a conducting rod Thus the ON position of a switch is one state of a switch called a closed state The other state of a switch is the open state when it is placed in the OFF position So a switch has two stable states There is another way to talk about the functioning of a switch We can denote a switch by x and use the values 0 and 1 to depict its two states i e to convey that x is open we write x 0 and to convey that x is closed we write x 1 see Fig 2 TXT These values which clcnote the state of a switch x are called the state values s v in short of that switch Boolean Algebra Circ x 1 x 0 Fig 2 OFF ON p tion

Algebra
Permutations and Combinationsthis definition Now using Tables 1 and 2 you can check that the five laws B1 B5 hold good Thus S par ser 1 0 1 is a Boolean algebra A Boolean algebra whose underlying set has only two elements is very important in the study of circuits We call such an algebra a two element Boolean algebra Throughout the unit we denote this algebra by B From this Boolean algebra we can build many more as in the following example Example 3 Let B BxBx x B e e2 en each e 0 or 1 for n 2 1 be the Cartesian product of n copies of B For ik jk 0 1 1 k n define 11 12 11 12 1 2 Jn i1Aj1 12 A 12 in jn Vi1 j2 11 12 in El a Then B is a Boolean algebra for all n 1 Solution Firstly observe that the case n 1 is the Boolean algebra B Now let us write 0 0 0 0 and I 1 1 1 for the two clcments of B consisting of n tuples of 0 s and 1 s respectively Using the fact that B is a Boolean algebra you can check that B3 with operations as clcfined above is a Boolean algebra for every n 2 1 in Vj1 12 Vj2 in Vin and The Boolean algebras B 121 called switching algebras are very useful for the study of the hardware and software of digital computers We shall now state without proof some other properties of Boolean algebras which can be deduced from the five laws B1 B5 Theorem 1 Lot B S V A O I be a Boolean algebra Then the following laws hold Vx y ES x V x x x Ax x a Idempotent laws b Absorption laws c Involution law d De Morgan s laws x V x Ay x x A XV y x x x xVy x Ay x Ay x Vy In fact you have already come across some of these properties for the Boolean algebra S of propositions in Unit 1 In the following exercise we ask you to verify them Verify the identity laws and absorption laws for the Boolean algebra S A V T F of propositions b Verify the absorption laws for the Boolean algebra P X U n X 1 In Theorem 1 you may have noticed that for each statement involving V and A there is an analogous statement with A instead of V and V instead of A This is not a coincidence as the following definition and result shows Definition Ifp is a proposition involving A and V the dual of P denoted by pd is the proposition obtained by replacing each occurrence of A and or V in p by V and or A respectively in p For example x V x A y x is the dual of x A x V y x Boolean A

Algebra
Permutations and CombinationsNow you should find it easy to solve the following exercise E4 Simplify tlie Boolean expression X X1 X2 X3 x1 A X2 V X1 AX2 A X3 V X2 AX3 With this we conclude this section In the next Section we shall give an important application of the concepts discussed here 3 4 LOGIC CIRCUITS If you loole around you would notice many electric or electronic appliances of daily use Sorne of them need a sirnple switching circuit to control the auto stop such as in a stereo system Some would use an auto power oil systeni used in transformers to control voltage fluctuations Each circuit is usually a combination of on off switches wirecl together in some specific configuration Nowadays certain types of electronic blocks i e solid state devices such as transistors resistors and capacitors are more in usc We call these electronic bloclcs logic gates or simply gates In Fig 5 we have shown a box which consists of some electronic switches or logic gates wired together in a specific manner Each line which is entering tlie box from the left represents an independent power source called input where all of them need not supply voltage to tlie box at a given moment A single line coming out of the box gives tlie final output of the circuit box The output depends on the type of input Input power lines Circuit Box Output lead Fig 5 A logic circuit This sort of arrangement of input power lines a circuit box and output lead is basic to all electronic circuits Throughout tlic unit any sucli interconnected assemblage of logic gates is referred to as a logic circuit As you may know computer hardwares are designed to handle only two levels of voltage both as inputs as well as outputs These two levels denoted by 0 and 1 are called bits an acronym for binary digits When the bits are applied to the logic gates by means of one or two wires input leads tlie output is again in the form of voltages 0 and 1 Roughly speaking you may think of a gate to be on or off according to whether the output voltage is at level 1 or 0 respectively Three basic types of logic gates are an AND gate an OR gate and a NOT gate We shall now define them one by one Definition Let the Boolean variables x and x2 represent any two bits An AND gate receives inputs x arid x2 and produces the output denoted by xi A x2 as given in Table 3 alongside The standard pictorial representation of an AND gate is shown in Fig 6 From the first three rows of Table 3 you can see that whenever the voltage in any one of the input wires of the AND gate is at level 0 then the output voltage of the gate is also at level 0 Boolean Algebra a Circu Table 3 Output X1 0 0 AND gat X2 X1 X2 0 0 1 1 0 0 0 1

Algebra
Permutations and Combinationsas an arbitrary even number arid not a particular value Why don t you try an exercise ngw E6 Give a direct proof of the statement If x is a real number such that x 9 then either x 3 or x 3 Let us now consider another proof strategy 2 3 2 Indirect Proofs In this sub section we shall consider two roundabout methods for proving p q Proof by contrapositive In the first method we use the fad that the proposition p q is logically equivalent to its contrapositive q p i e p q q p For instance If Ammu does not agree with communalists then she is not orthodox is the same as If Ammu is orthodox then she agrees with communalists Because of this equivalence to prove p q wc can instead prove q p This means that we can assume that q is true and then try to prove that p is true In other words what we do to prove p q in this method is to assume that q is false and then show that p is false Let us consider an example Example 4 Prove that If x y EZ such that xy is odd then botli x and y are odd by proving its contrapositive Solution Let us name the statements involved as below P xy is odd q both x and y are odd So p xy is even and q x is even or y is even or both are even We want to prove p q by proving that q p So we start by assuming that q is true i c we suppose that x is even Then x 2ii for some n E N Therefore xy 2ny Therefore xy is even by definition That is p is true So we have shown that q p Therefore p q S f Why don t you try some related exercises now E7 Write down the contrapositive of the statement If f is a 1 1 function from a finite set X into itself then f must be surjective E8 Prove the statement If x is an integer and x is even then x is also even by proving its contrapositive And now let us consider the other way of proving a statement indirectly

Algebra
Permutations and Combinations2 3 DIFFERENT METHODS OF PROOF In this section we shall consider three different strategies for proving a statement We will also discuss a method that is used only for disproving a statement Let us start with a proof strategy based on the first rule of inference that we discussed in the previous section 2 3 1 Direct Proof This form of proof is based entirely on modus ponens Let us formally spell out the strategy Definition A direct proof of p q is a logically valid argument that begins with the assumption that p is true and in one or more applications of the law of detachment concludes that q must be true So to construct a direct proof of p q we start by assuming that P is true Then in one or more steps of the form p 9 9192 9n q we conclude that q is true Consider the following examples 1 Example 2 Give a direct proof of the statement The product of two odd integers is odd Solution Let us clearly analyse what our hypotheses are and what we have to prove We start by considering any two odd integers x and y So our hypothesis is p x and y are odd The conclusion we want to reach is q xy is odd 9 Let us first prove that P Since x is odd x 2m 1 for some integer m Similarly y 2n 1 for some integer n Then xy 2m 1 2n 1 2 2mn m n 1 Therefore xy is odd So we have shown that p q Now we can apply modus ponens to p A p q to get the required conclusion Note that the essence of this direct proof lies in showing p q b Exar 3 Give a direct proof of the theorem The square of an even integer is an even integer Solution First of all let us write the given statement symbolically as VxEZ p x q x where p x x is even and q x x is even i e q x is the same as p x The direct proof then goes as follows Let x be an even number i e we assume p x is true Then x 2n for some integer n we apply the definition of an even number

Algebra
Permutations and Combinationsns 1 P i T TTT F T 1 F Table 1 qpq p a A p T F T F F F 1 The last column gives the truth values of the premises The first column gives the corresponding truth values of the conclusion Now the argument will only be valid if whenever both the premises are true the conclusion is true This happens in the first row but not in the third row Therefore the argument is not valid Why don t you check an argument for validity now F T T E3 Check whether the following argument is valid pqV r q p pr You have seen that a proof is a logical argument that verifies the truth of a theorem There are several ways of proving a theorem as you will see in the next section All of them are based on one or more rules of inference which are different forms of arguments We shall now present four of the most commonly used rules Law of detachment or modus ponens Consider the following argument If Kali can draw she will get a job Kali can draw Therefore she will get a job To study the form of the argument let us take p to be the proposition Kali can draw and q to be the proposition Kali will get a job Then the premises are pq and p The conclusion is q So the form of the argument is P q P q Is this argument valid To find out let s construct its truth table see Table 2 Table 2 Truth table for p q A p q i e pq Ap q I P q P q pa p T T T T F F F T F F F T F In the table look at the second column the conclusion and the fourth T F CL

Algebra
Permutations and CombinationsSolution Let us start by assuming A is a truth teller What A says is true B is a truth teller What B says is true A and B are of opposite types This is a contradiction because our premises say that A and B are both truth tellers The assumption we started with is false A always tells lies What A has told you is a lie B always tells lies A and B are of the same type i e both of them always lie Here are a few exercises for you now While doing them you would realise that there are situations in which all the three methods of proof we have discussed so far can be used E9 Use the method of proof by contradiction to show that i 3 is irrational ii For x E R if x 4x 0 then x 0 6 E10 Prove E 9 ii directly as well as by the method of contrapositive E11 Suppose you are visiting the village described in Example 7 above Another two villagers C and D approach you C tells you Both of us always tell the trutli and D says C always lies What types are C and D Let us now consider the problem of showing that a statement is falsc 2 3 3 Counterexamples Suppose I make the statement All human beings are 5 feet tall You are quite likely to show me an example of a human being standing nearby for whom the statement is not true And as you know the moment we have even one example for which the statement Vx p x is false i e 3x p x is true then the statement is false An example that shows that a statement is false is a counterexample to such a statement The name itself suggests that it is an example to counter a given statement A common situation in which we look for counterexamples is to disprove statements of the form p q From Unit 1 you know that p q PA q Therefore a counterexample to p where p q is true i e p is true and holds but the conclusion q does not hold q needs to be an example q is true i e the hypothesis p For instance to disprove the statement If n is an odd integer then n is prime we need to look for an odd integer which is not a prime number 15 is one such integer So n 15 is a counterexample to the given statement Notice that a counterexample to a statement p proves that P is false i e p is true Let us consider another example Example 8 Disprove the following statement VaR VbER a b a b

Algebra
Permutations and Combinations4 5 Proof by contradiction In this method to prove q is true we start by assuming that q is false i e q is true Then by a logical argument we arrive at a situation where a statement is true as well as false i e we reach a contradiction r r for some statement r This means that the truth of q implies a contradiction a staternent that is always false This can only happen when q is false also Therefore q must be true This method is called proof by contradiction It is also called reductio ad absurdum a Latin phrase because it relies on reducing a given assumption to an absurdity Let us consider an example of the use of this method Example 5 Show that 5 is irrational Solution Let us try and prove the given statement by contradiction For this we begin by assuming that 5 is rational This rneans that there exist positive integers a and b such that 5 where a and b have no common a b factors This implies a 5b a 5b 5 a 5 a Therefore by definition a 5c for some c E Z Therefore a 25c But a 5b also So 25c 5b2 5c b 5 b 5 b AD But now we find that 5 divides both a and b which contradicts our e assumption that a and b have no common factor Therefore we conclude that our assumption that 5 is rational is false i e 5 is irrational We can also use the method of contradiction to prove an implication r s Here we can use the equivalence rs rAs So to prove r s we can begin by assuming that r s is false i e r is true and s is false Then we can present a valid argument to arrive at a contradiction Consider the following example from plane geometry Example 6 Prove the following If two distinct lines L and La intersect then their intersection consists of exactly one point Solution To prove the given implication by contradiction let us begin by assuming that the two distinct lines L and L2 intersect in more than one point Let us call two of these distinct points A and B Then both L and L2 contain A and B This contradicts the axiom from geomctry that says Given two distinct points there is exactly one line containing them Therefore if L and L2 intersect then they must intersect in only one point The contradiction rule is also used for solving many logical puzzles by discarding all solutions that reduce to contradictions Consider the following example those Example 7 There is a village that consists of two types of people who always tell the truth and those who always li Suppose that you visit the village and two villagers A and B come up to you Further suppose A says B always tells the truth and B says A and I are of opposite types What types are A and B 8
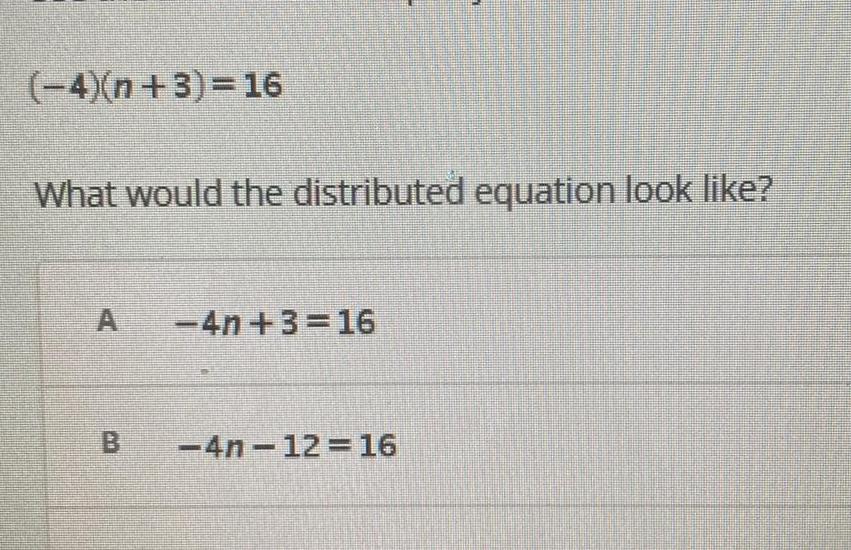
Algebra
Permutations and Combinations4 n 3 16 What would the distributed equation look like 4n 3 16 4n 12 16

Algebra
Permutations and CombinationsSolve each equation Describe the number of solutions one none or infinitely many 13 3x1 11 12 5x 4 8 5x 37443815X

Algebra
Permutations and CombinationsExpansion along first Row R 11 Step 1 Multiply first element a of R by 1 1 1 sum of suffixes in a11 and with the second order determinant obtained by deleting the elements of first row R and first column C of A as a lies in R and C i e 922 923 1 a 932 A33 Step 2 Multiply 2nd element a of R by 1 2 1 sum of suffixes in a order determinant obtained by deleting elements of first row R and 2nd column C of A as a 12 lies in R and C i e 1 2 a 2 Step 3 Multiply third element a 3 of R by 1 3 1 sum of suffixes in a and the second order determinant obtained by deleting elements of first row R and third column C of A as a 3 lies in R and C3 or 1 3a13 250 1951 i e Step 4 Now the expansion of determinant of A that is A written as sum of all three terms obtained in steps 1 2 and 3 above is given by 145 a31 932 922 a23 1 det A A 1 32 33 1 3 a a21 922 931 932 A a a22 a33 a32a23 12 a 1 a33 a31a23 a13 a 1 a32 931 922 a13 a 1 a22 A33 11 a 13 a31 a22 Note We shall apply all four steps together Expansion along second row R Expanding along R we get A 1 1 a Rationalised 2023 24 a11 a32a23 a 12 a21 a 33 a11 A a21 a 31 923 921 a32 A33 1 a12 a13 1 all a31 912 1 3 a21 a12 a33 a32 a 13 a22 a23 a11 a32 a31 9 2 a12 932 a 1 2 912 923 931 933 a13 22 23 a32 a33 RT 922 aus de 912 and the second all a13 a31 DETERMINANTS 79 a12 a31 a23 a13 a21 a32 a31 a 13 1 published

Algebra
Permutations and CombinationsTheorem 1 If A be any given square matrix of order n then A adj A adj A A A I where I is the identity matrix of order n Verification a13 a23 931 932 933 Since sum of product of elements of a row or a column with corresponding cofactors is equal to A and otherwise zero we have Let 911 912 A 9 1 922 A adj A Let 2 A11 A21 A31 then adj A A12 A22 A32 A13 A23 A33 Rationalised 2023 24 A 0 0 0 A 0 0 A 0 A 0 1 Similarly we can show adj A A A I Hence A adj A adj A A A I Definition 4 A square matrix A is said to be singular if A 0 For example the determinant of matrix A Hence A is a singular matrix Definition 5 A square matrix A is said to be non singular if A oto A Then 4 hed 2 3 4 A 5 48 3 Hence A is a nonsingular matrix We state the following theorems without proof 00 A Remark We know that adj A A A I 0 0 00 1 0 A I is zero Theorem 2 If A and B are nonsingular matrices of the same order then AB and BA are also nonsingular matrices of the same order Theorem 3 The determinant of the product of matrices is equal to product of their respective determinants that is AB A B where A and B are square matrices of the same order DETERMINANTS 89 A 0 0 Writing determinants of matrices on both sides we have O 0 A 0 A 0 0 A
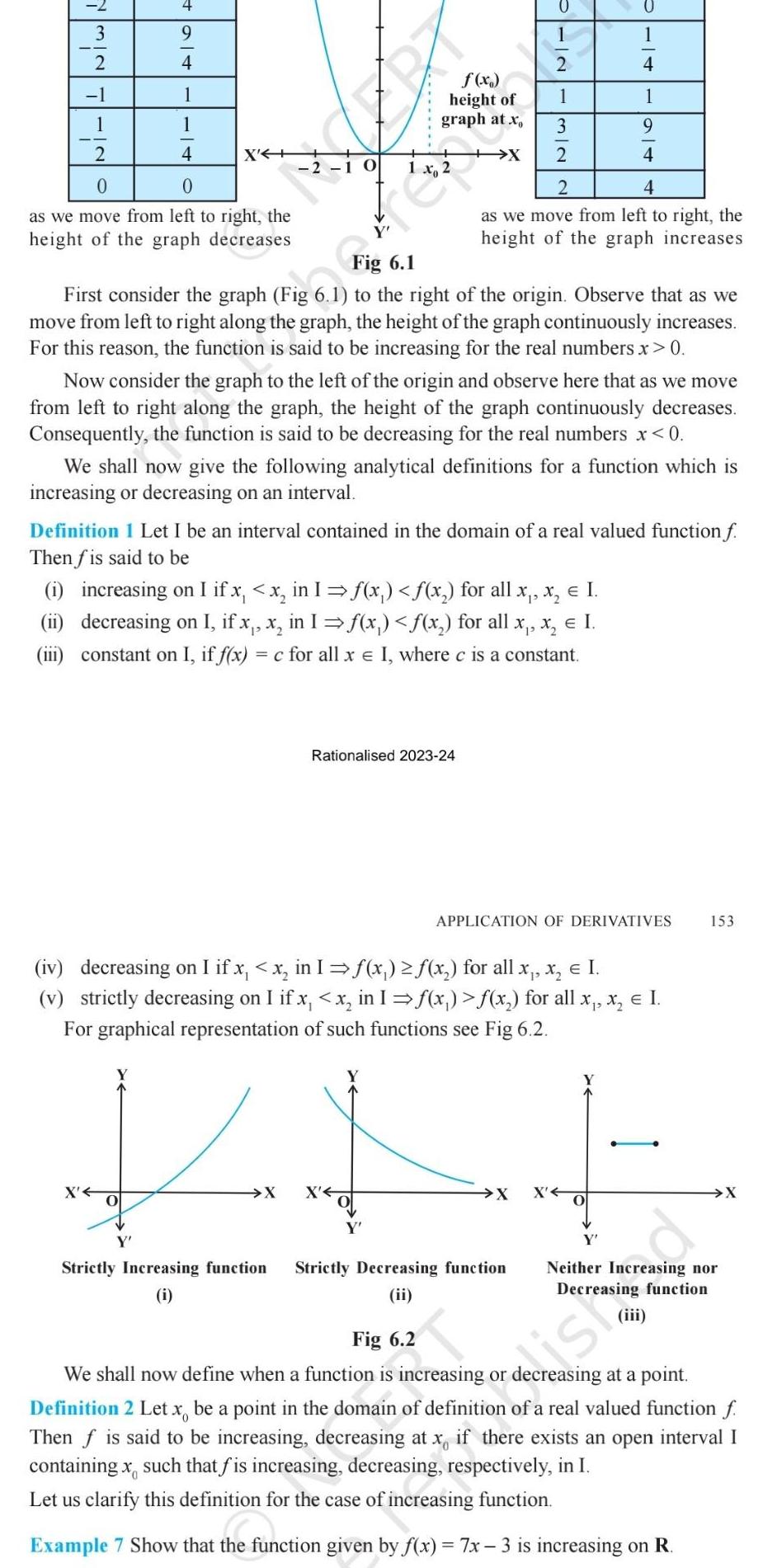
Algebra
Permutations and Combinations32 4 1 1 4 0 as we move from left to right the height of the graph decreases 2 1 X J X f x height of graph at x O PINN Fig 6 1 First consider the graph Fig 6 1 to the right of the origin Observe that as we move from left to right along the graph the height of the graph continuously increases For this reason the function is said to be increasing for the real numbers x 0 Strictly Increasing function i 1 Now consider the graph to the left of the origin and observe here that as we move from left to right along the graph the height of the graph continuously decreases Consequently the function is said to be decreasing for the real numbers x 0 Rationalised 2023 24 X X 2 We shall now give the following analytical definitions for a function which is increasing or decreasing on an interval 3 Definition 1 Let I be an interval contained in the domain of a real valued function f Then f is said to be i increasing on I if x x in 1 f x x for all x x I ii decreasing on I if x x in I x x for all x x I iii constant on I if f x c for all x I where c is a constant 2 Fig 6 2 2 4 as we move from left to right the height of the graph increases iv decreasing on I if x x in I f x x for all x x I v strictly decreasing on I if x x in 1 x x for all x x I For graphical representation of such functions see Fig 6 2 Strictly Decreasing function ii 4 1 9 4 APPLICATION OF DERIVATIVES X X O 153 ist X Neither Increasing nor Decreasing function 20 We shall now define when a function is increasing or decreasing at a point Definition 2 Let x be a point in the domain of definition of a real valued function f Then f is said to be increasing decreasing at x if there exists an open interval I containing x such that fis increasing decreasing respectively in I Let us clarify this definition for the case of increasing function Example 7 Show that the function given by f x 7x 3 is increasing on R

Algebra
Permutations and CombinationsIn other words kA k a mxn k a mx n that is i j th element of kA is ka for all possible values of i and j For example if 46 notto MATHEMATICS For example let 1 5 7 2 Example 7 If A Solution We have 3A 3 5 Negative of a matrix The negative of a matrix is denoted by A We define A 1 A 1 2 3 2 31 0 5 3 1 1 5 7 3 2 0 5 2A B 2 1 5 3 21 2 och mot 3 1 A 1 A 1 5 X Difference of matrices If A a B b are two matrices of the same order say mxn then difference A B is defined as a matrix D d where d a b for all value of i and j In other words D A B A 1 B that is sum of the matrix A and the matrix B and B then Rationalised 2023 24 3 A 5 9 3 4 5 3 5 21 9 6 0 15 1 2 3 2 3 3 1 1 0 2 4 6 462 3 then A is given by 2 3 1 1 3 H 1 1 0 2 then find 2A B A B a b a b X 2 3 4 1 6 3 1 3 4 1 6 0 2 2 5 60 5 3 4 3 Properties of matrix addition tion The addition of matrices satisfy the following properties i Commutative Law If A a B b are matrices of the same order say mx n then A B B A Now blished b a addition of numbers is commutative b a B A ii Associative Law For any three matrices A a B b C c of the same order say mx n A B C A B C
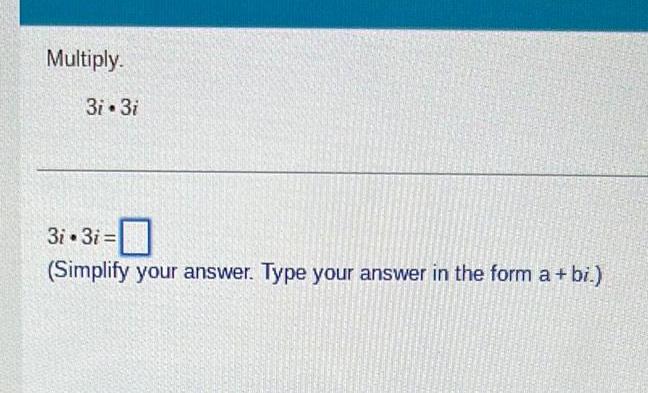
Algebra
Permutations and CombinationsMultiply 3i 3i 3i 3i 0 Simplify your answer Type your answer in the form a bi

Algebra
Permutations and CombinationsStep 2 Formulation We are given that the costs are of two types fixed and variable The fixed costs are independent of the number of units produced e g rent and rates while the variable costs increase with the number of units produced e g material Initially we assume that the variable costs are directly proportional to the number of units produced this should simplify our model The company earn a certain amount of money by selling its products and wants to ensure that it is maximum For convenience we assume that all units produced are sold immediately The mathematical model Let x number of units produced and sold C total cost of production in rupees I income from sales in rupees P profit in rupees Our assumptions above state that C consists of two parts i fixed cost a in rupees ii variable cost b rupees unit produced Then C a bx Also income I depends on selling price s rupees uni Thus I Sx The profit P is then the difference between income and costs So s b x a independent dependent 3 We now have a mathematical model of the relationships 1 to 3 between the variables x C I P a b s These variables may be classified as Rationalised 2023 24 ot to be published X C I P parameters a b s The manufacturer knowing x a b s can determine P Step 3 From 3 we can observe that for the break even point i e make neither profit a nor loss he must have P 0 i e x units s b Steps 4 and 5 In view of the break even point one may conclude that if the company produces few units i e less than x units then the company will suffer loss s b a dP dx 1 s b MATHEMATICAL MODELLING a s b and if it produces large number of units i e much more than units then it can make huge profit Further if the break even point proves to be unrealistic then another model could be tried or the assumptions regarding cash flow may be modified Remark From 3 we also have 205 This means that rate of change of P with respect to x depends on the quantity h which is the difference of selling price and the variable cost of each product

Algebra
Permutations and CombinationsIntroduction A inventory may be defined as an idle resources that possesses economic value It is an item stored or reserved for meeting future demand Such items may be materials machines many or even human resources Reasons for holding storks The main reasons are 1 To ensure sufficient goods one are available to meet anticipated demands 2 To absorb variations in demand and production 3 To prove a buffer between production processor 4 To take advantage of bulk purchasing discounts 5 To meet possible shortages in the future 6 To enable produces process to flow smoothly and efficiently 7 As deliberate investment policy particularly in times of inflation or possible shortages The Objective of Inventory Control The objective of inventory control is to maintain stock levels so that the combined costs mentioned earlier are at amenities This is done by establishing two sectors how to order When to order Inventory control terminologies 1 Demand The amount of quantity required by sales or products usually expressed as the rate of demand for week or month or year etc 2 Economic order quantity EOQ This is a calculated ordering quantity which minimized the balance between inventory holding costs and re order costs 3 Lead time The period of time between ordering and replenishment 4 Butter stock or safety stock It is a stock allowance to cover errors in forecasting the lead time on the demand during the lead time 54 5 Maximum stock A stock level as the maximum desirable which is used as an indicator 6 Reorder level The level of stock of which culture replacement order should be placed The re order level 9 independent upon the lead time and the demand upon the lead time and the demand during the lead time Types of Inventory Models There are two types of models can be used for inventory control They are i deterministic model ii stochastic model

Algebra
Permutations and CombinationsP t AP t 2P 1 t n 0 Po t AP t n 0 Po t At Po t lim At At 0 1 0 1 Multiplying both sides of A by z and taking summation for n 1 2 00 we get En0 Pn t z En 1 Pn t z En 1 Pn 1 t 2 Log P z t M z 1 t E To determine E we put t 0 to get Log P z 0 E P z 0 02 P 0 P z t ed 2 1 Now Pn t can be defined as P z t P t dp z t 0 P z t at e at n P z t P 1 2 n 0 P z t P z t AP t In general P t Classification of queueing models I Probabilistic queueing models 00 P t zn R 0 46 z 1 Model I Erlang Model This model is symbolically represented by MIMI co FCFS this denotes poisson arrival exponential inter arrival poisson departure exponential service time single server infinite capacity and first come first served service discipline Model II General Erlang Model Although this model is also represented by MIMI 00 FCFS but this is a general queueing model in which the rate of arrival and service depend on the length n of the line Model III this model represented by MIMI NFCFS In this model capacity of the system is limited finite say n Obviously the number of arrivals will not exceed the number N in any case Model IV This model is represented by MMS 0o FCFS in which the number of stations is s in parallel 46
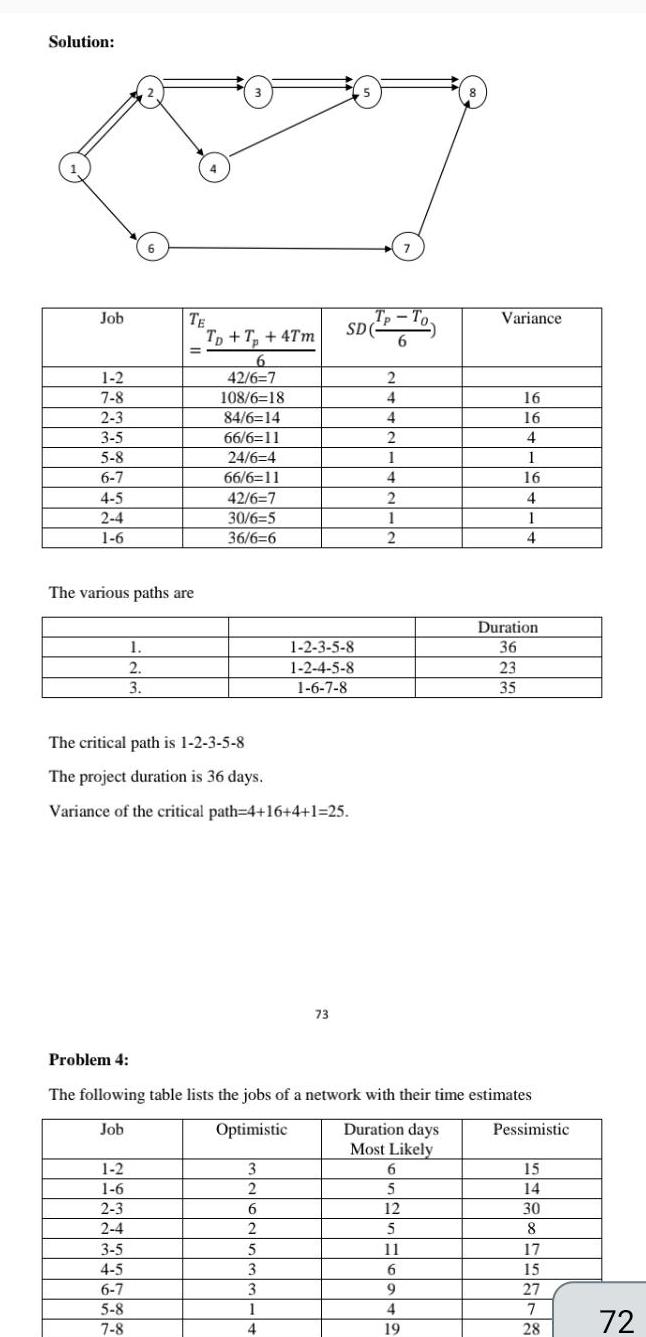
Algebra
Permutations and CombinationsSolution Job 1 2 7 8 2 3 3 5 5 8 6 7 4 5 2 4 1 6 6 The various paths are 1 2 3 1 2 1 6 2 3 TE 2 4 3 5 4 5 6 7 5 8 7 8 Tp T 4Tm 6 42 6 7 108 6 18 84 6 14 66 6 11 24 6 4 66 6 11 42 6 7 30 6 5 36 6 6 The critical path is 1 2 3 5 8 The project duration is 36 days Variance of the critical path 4 16 4 1 25 3 2 6 2 5 3 3 SD TP 1 2 3 5 8 1 2 4 5 8 1 6 7 8 1 4 73 2 4 4 2 1 4 2 1 2 Problem 4 The following table lists the jobs of a network with their time estimates Job Optimistic Duration days Most Likely 7 6 6 5 12 5 11 6 9 4 19 Variance 16 16 4 1 16 4 1 4 Duration 36 23 35 Pessimistic 15 14 30 8 17 15 27 7 28 72

Algebra
Permutations and Combinations154 MATHEMATICS Proof a Let x x a b be such that x x Then by Mean Value Theorem Theorem 8 in Chapter 5 there exists a point c between and X x such that i e i e Thus we have Rationalised 2023 24 f x f x f c x x f x f x 0 f x f x X x Hence f is an increasing function in a b f x f x for all x x a b is increasing on R Solution Note that The proofs of part b and c are similar It is left as an exercise to the Remarks There is a more generalised theorem which states that if f x for x in an interval excluding the end points and fis continuous in the interval then fis increasing Similarly if f x 0 for x in an interval excluding the end points and fis continuous in the interval then fis decreasing Example 8 Show that the function f given by f x 3x 6x 4 as f c 0 given 3 x 2x 1 1 t to be po hod 3 x 1 1 0 in every interval of R Therefore the function fis increasing on R Example 9 Prove that the function given by f x cos x is a decreasing in 0 b increasing in 1 2 and c neither increasing nor decreasing in 0 2

Algebra
Permutations and CombinationsIs the function f defined by 2x 3 if x 2 2x 3 if x 2 6 f x x 8 f x x 0 continuous at x 0 At x 1 At x 2 Find all points of discontinuity off where fis defined 10 f x if x 0 if x 0 x 1 if x 1 x 1 if x 1 udenly she x 0 1 if x 1 12 f x if x 1 13 Is the function defined by a continuous function f x User f x x if x 1 2 if x 1 16 f x 2x if 1 x 1 2 if x 1 5 if x 1 x 3 if x 3 f x 2x if 3 x 3 6x 2 if x 3 11 f x 9 f x x x 5 if x 1 x 5 if x 1 Rationalised 2023 24 x if x 0 1 1 if x 0 x 3 if x 2 x 1 if x 2 CONTINUITY AND DIFFERENTIABILITY Discuss the continuity of the function f where f is defined by 3 if 0 x 1 14 f x 4 if 1 x 3 5 if 3 x 10 2x if x 0 15 f x 0 if 0 x 1 4x if x 1 is continuous at x 3 18 For what value of 2 is the function defined by 17 Find the relationship between a and b so that the function f defined by ax 1 if x 3 f x bx 3 if x 3 2 x 2x if x 0 4x 1 117 olished f x continuous at x 0 What about continuity at x 1 19 Show that the function defined by g x x x is discontinuous at all integral points Here x denotes the greatest integer less than or equal to x 20 Is the function defined by f x x sin x 5 continuous at x

Algebra
Permutations and Combinations4 9 is continuous at x c provided g c 0 Proof We are investigating continuity of f g at x c Clearly it is defined at x c We have 114 lim f g x lim f x g x X C MATHEMATICS Hence f g is continuous at x c Proofs for the remaining parts are similar and left as an exercise to the reader lim f x lim g x X C X C function defined by f c g c f g c Rationalised 2023 24 Remarks 1 As a special case of 3 above if f is a constant function i e f x 2 for some real number then the function 2 g defined by g x g x is also continuous In particular if 1 the continuity of fimplies continuity of f ii As a special case of 4 above if f is the constant function f x 2 then the 2 g you by definition of f g by the theorem on limits as fand g are continuous by definition of f g 2 2 x is also continuous wherever g x 0 In g x g particular the continuity of g implies continuity of g The above theorem can be exploited to generate many continuous functions They also aid in deciding if certain functions are continuous or not The following examples illustrate this Example 16 Prove that every rational function is continuous Solution Recall that every rational function fis given by Bird q x 0 P x f x 9 x where p and q are polynomial functions The domain off is all real numbers except points at which q is zero Since polynomial functions are continuous Example 14 fis continuous by 4 of Theorem 1 Example 17 Discuss the continuity of sine function Solution to see this we use the following facts lim sin x 0 X 0 We have not proved it but is intuitively clear from the graph of sin x near 0 Now observe that f x sin x is defined for every real number Let c be a real xc we know that h 0 Therefore number Put x c h lim f x lim sin x X C X C lim sin c h h 0 blishe lim sin ccos h cosc sin h h 0 lim sinc cos h lim cos c sin h

Algebra
Permutations and Combinations4 is continuous at x c provided g c 0 8 Proof We are investigating continuity of f g at x c Clearly it is defined at x c We have 114 im f g x lim f x g x X C MATHEMATICS Hence f g is continuous at x c Proofs for the remaining parts are similar and left as an exercise to the reader function defined by lim f x limg x X C X C f c g c f g c Rationalised 2023 24 Remarks i As a special case of 3 above iffis a constant function i e f x 2 for some real number 2 then the function 2 g defined by 2 g x 2 g x is also continuous In particular if 1 the continuity of fimplies continuity of f ii As a special case of 4 above if f is the constant function f x 2 then the x is also continuous wherever g x 0 In g x a 2 2 g 8 not 1 particular the continuity of g implies continuity of g The above theorem can be exploited to generate many continuous functions They also aid in deciding if certain functions are continuous or not The following examples illustrate this by definition of f g by the theorem on limits as fand g are continuous by definition of f g Example 16 Prove that every rational function is continuous Solution Recall that every rational function fis given by q x 0 f x P x 9 x where p and q are polynomial functions The domain offis all real numbers except points at which q is zero Since polynomial functions are continuous Example 14 fis continuous by 4 of Theorem 1 Example 17 Discuss the continuity of sine function Solution to see this we use the following facts lim sin x 0 x 0 We have not proved it but is intuitively clear from the graph of sin x near 0 Now observe that f x sin x is defined for every real number Let c be a real number Put x c h If x c we know that h 0 Therefore lim f x X C lim sin x X C lim sin c h h 0 blishe lim sin c cos h cosc sinh h 0

Algebra
Permutations and Combinationsii No element of E is related to any element of O and vice versa iii E and O are disjoint and Z EUO The subset E is called the equivalence class containing zero and is denoted by 0 Similarly O is the equivalence class containing 1 and is denoted by 1 Note that 0 1 0 2r and 1 2r 1 r Z Infact what we have seen above is true for an arbitrary equivalence relation R in a set X Given an arbitrary equivalence relation R in an arbitrary set X R divides X into mutually disjoint subsets A called partitions or subdivisions of X satisfying i all elements of A are related to each other for all i ii no element of A is related to any element of A iii UA X and A A 0 i j The subsets A are called equivalence classes The interesting part of the situation is that we can go reverse also For example consider a subdivision of the set Z given by three mutually disjoint subsets A A and A hose union is Z with A x Z x is a multiple of 3 6 3 0 3 6 A x Z x 1 is a multiple of 3 5 2 1 4 7 A x Z x 2 is a multiple of 3 4 1 2 5 8 Define a relation R in Z given by R a b 3 divides a b Following the arguments similar to those used in Example 5 we can show that R is an equivalence relation Also A coincides with the set of all integers in Z which are related to zero A coincides with the set of all integers which are related to 1 and A coincides with the set of all integers in Z which are related 2 Thus A 0 A 1 and A 2 In fact A 3r A 3r 1 and A 3r 2 for all r Z Example 6 Let R be the relation defined in the set A 1 2 3 4 5 6 7 by R a b both a and b are either odd or even Show that R is an equivalence relation Further show that all the elements of the subset 1 3 5 7 are related to each other and all the elements of the subset 2 4 6 are related to each other but no element of the subset 1 3 5 7 is related to any element of the subset 2 4 6 Rationalised 2023 24 RELATIONS AND FUNCTIONS E Solution Given any element a in A both a and a must be either odd or even so that a a e R Further a b R both a and b must be either odd or even b a R Similarly a b R and b c R all elements a b c must be either even or odd simultaneously a c R Hence R is an equivalence relation Further all the elements of 1 3 5 7 are related to each other as all the elements of this subset are odd Similarly all the elements of the subset 2 4 6 are related to each other as all of them are even Also no element of the subset 1 3 5 7 can be related to any element of 2 4 6 as elements of 1 3 5 7 are odd while elements of 2 4 6 are even EXERCISE 1 1 1 Determine whether each of the following relations are reflexive syr transitive 5 1 Relation R in the set A 1 2 3 13 14 defined R x y 3x y 0 ii Relation R in the set N of natural numbers defined as
Algebra
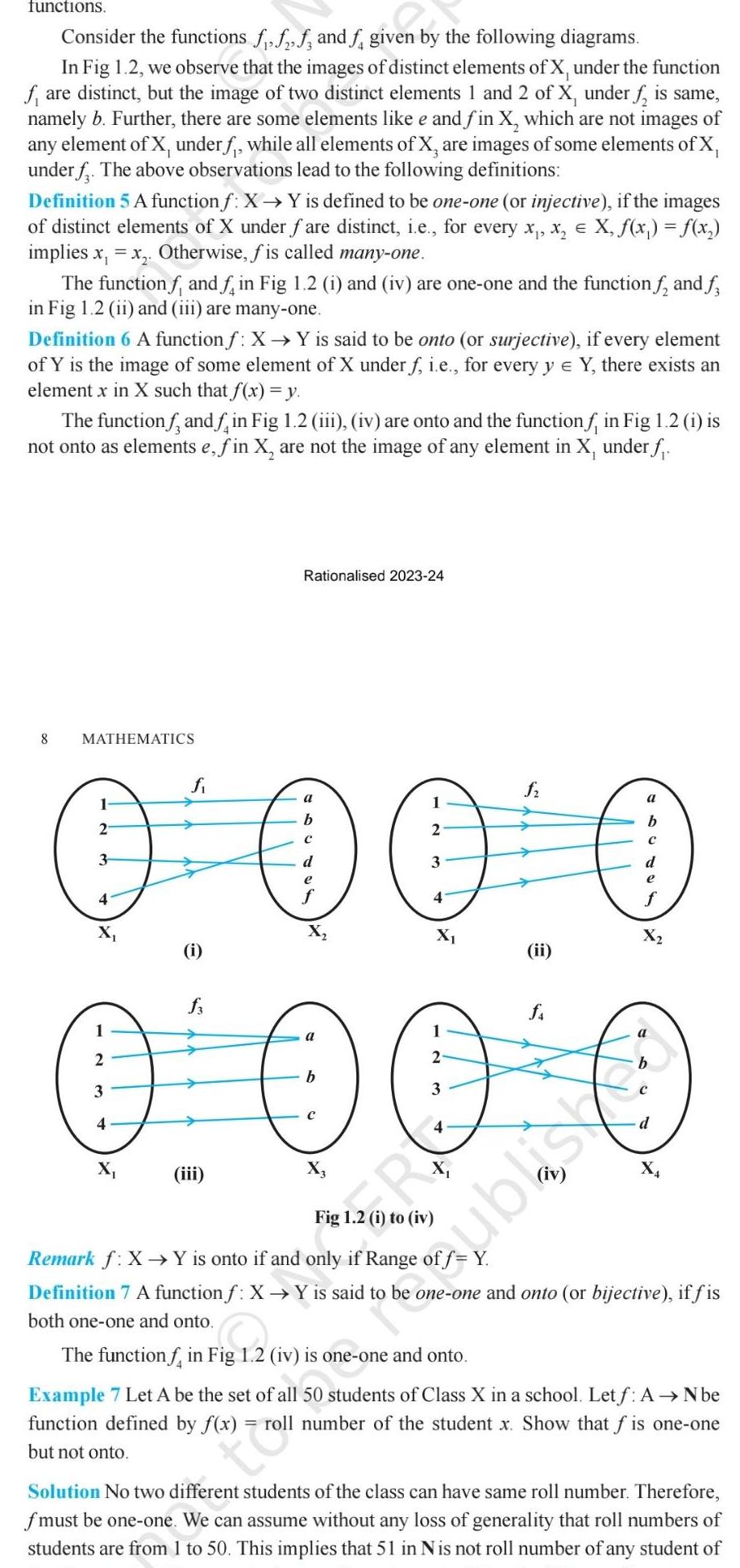
Permutations and Combinationsfunctions Consider the functions fff and f given by the following diagrams In Fig 1 2 we observe that the images of distinct elements of X under the function fare distinct but the image of two distinct elements 1 and 2 of X under f is same namely b Further there are some elements like e and fin X which are not images of any element of X under f while all elements of X are images of some elements of X under f The above observations lead to the following definitions Definition 5 A function f X Y is defined to be one one or injective if the images of distinct elements of X under fare distinct i e for every x x X f x f x implies x x Otherwise fis called many one The function f and f in Fig 1 2 i and iv are one one and the function f and f in Fig 1 2 ii and iii are many one Definition 6 A function f X Y is said to be onto or surjective if every element of Y is the image of some element of X under f i e for every y Y there exists an element x in X such that f x y The function and in Fig 1 2 iii iv are onto and the function f in Fig 1 2 i is not onto as elements e fin X are not the image of any element in X under f 8 MATHEMATICS fi a 1 1 a b 2 2 3 d 3 e e 4 4 X X O O O O 0 0 0 0 a 2 2 b 3 3 4 4 iii Rationalised 2023 24 i ii shari Remark f X Y is onto if and only if Range of f Y Definition 7 A function f X Y is said to be one one and onto or bijective if fis both one one and onto The function f in Fig 1 2 iv is one one and onto Example 7 Let A be the set of all 50 students of Class X in a school Let f A N be function defined by f x roll number of the student x Show that f is one one but not onto troll Solution No two different students of the class can have same roll number Therefore fmust be one one We can assume without any loss of generality that roll numbers of students are from 1 to 50 This implies that 51 in Nis not roll number of any student of

Algebra
Permutations and Combinationsthe class so that 51 can not be image of any element of X under f Hence fis not onto Example 8 Show that the function f N N given by f x 2x is one one but not onto Solution The function f is one one for f x f x 2x 2x x x Further fis not onto as for 1 N there does not exist any x in N such that f x 2x 1 X Rationalised 2023 24 Example 9 Prove that the functionf R R given by f x 2x is one one and onto Solution f is one one as f x f x 2x 2x x x Also given any real number y in R there exists in R such that f 2 2 1 y Hence f is onto 12 02 f x Y Example 10 Show that the function f N N for every x 2 is onto but not one one O is both one one and onto RELATIONS AND FUNCTIONS x 1 if x is odd x 1 if x is even CERT y f x 2x Example 11 Show that the function f R R defined as f x x is neither one one nor onto Solution Since f 1 1 f 1 f is not one one Also the element 2 in the co domain Ris not image of any element x in the domain R Why Therefore f is not onto X Example 12 Show that f N N given by X Solution fis not one one as f 1 f 2 1 But fis onto as given any y N y 1 we can choosex as y 1 such that f y 1 y 1 1 y Also for 1 N we have f 1 1 f 1 2 1 and f x x 1 1 1 x 1 Published O 9 f x x f 1 1 x 1 Y The image of 1 and 1 under f is 1 Fig 1 4

Algebra
Permutations and CombinationsSolution Suppose f x f x Note that if x is odd and x is even then we will have x 1 x 1 i e x x 2 which is impossible Similarly the possibility of x being even and x being odd can also be ruled out using the similar argument Therefore both x and x must be either odd or even Suppose both x and x are odd Then f x f x x 1 x 1 x x Similarly if both x and x are even then also f x f x x 1 x 1 x x Thus fis one one Also any odd number 2r 1 in the co domain N is the image of 2r 2 in the domain N and any even number 2r in the co domain N is the image of 2r 1 in the domain N Thus fis onto Example 13 Show that an onto function f 1 2 3 1 2 3 is always one one Solution Suppose fis not one one Then there exists two elements say 1 and 2 in the domain whose image in the co domain is same Also the image of 3 under f can be only one element Therefore the range set can have at the most two elements of the co domain 1 2 3 showing that f is not onto a contradiction Hence fmust be one one Example 14 Show that a one one function f 1 2 3 1 2 3 must be onto Solution Since fis one one three elements of 1 2 3 must be taken to 3 different elements of the co domain 1 2 3 under f Hence fhas to be onto Remark The results mentioned in Examples 13 and 14 are also true for an arbitrary finite set X i e a one one function f X X is necessarily onto and an onto map f X X is necessarily one one for every finite set X In contrast to this Examples 8 and 10 show that for an infinite set this may not be true In fact this is a characteristic difference between a finite and an infinite set EXERCISE 1 2 1 Show that the function f R R defined by f x iii f R iv f N N x where R is the set of all non zero real numbers Is the result true if the domain R is replaced by N with co domain being same as R 1 2 Check the injectivity and surjectivity of the following functions i f N N given by f x x ii f Z Z given by f x x Rationalised 2023 24 is one one and onto R given by f x x given by f x x v f Z Z given by f x x 3 Prove that the Greatest Integer Function f R R given by f x x is neither one one nor onto where x denotes the greatest integer less than or equal to x 1 if x 0 f x 0 if x 0 1 if x 0 RELATIONS AND FUNCTIONS 11 4 Show that the Modulus Functionf R R given by f x x is neither one one nor onto where x is x if x is positive or 0 and x is x if x is negative 5 Show that the Signum Function f R R given by is neither one one nor onto 6 Let A 1 2 3 B 4 5 6 7 and let f 1 4 2 5 3 6 be a function from A to B Show that fis one one

Algebra
Permutations and CombinationsModel IV Manufacturing model with shortage 1 Demand D is uniform at a rate of runits per unit time 2 Production rate is finite say kor units per unit time 3 Shortages are allowed and have logged 4 Zero lead time 5 C inventory carrying cost per unit time 6 C shortage cost per unit line 7 Cs set up cost per run Optimal order quantity S v Over all annual cent 1000x100 2DC Cs C 1 01 306 Minimum cost Q Q G 1 G C t minimum cost in r Cs Q Solution k 2csr C C C 1 F 2r C C Cs 1 7 C C Worked Example 1 An item is produced at the rate of 50 items per day The demand occuss at the rate of 25 items per day If the setup cost is Rs 100 per set up and holding cost is Rs 0 01 per unit of item per day Find the economics lot size for one run assumes that the shortages are not allowed Also find the time fo cycle and the minimum total cost of one run 100000 2x1000x20x160x Rs 2 csr C C C C 1 1 50 perday 25 per days Rs 100 D 001 63