Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Geometry
2D GeometrySketch an angle 8 in standard position such that has the least possible positive measure and the point 5 12 is on the terminal side of 0 Then find the values of the six trigonometric functions for the angle Rationalize denominators if applicable Do not use a calculator Choose the correct graph below O A 18 18 Ay 18 O B 9 18 15 18 Q O C 18 k 18 18 o G


Geometry
Coordinate systemPerform the following calculations and express the result in the correct units and number of significant figu 47 0 m 2 2 S 1 2 140 cm x 35 cm 5 88 kg 200 m 3 4 0 00 50 m x 0 042 m 300 3 L 180 s 5 6 33 00 cm x 2 70 cm 35 000 kJ 0 250 min 8 22 0 m 5 28 m 15 5 m 7 9 0 042 kg 1 229 kg 0 502 kg 10 170 cm 3 5 cm 28 cm


Geometry
AreaWhat is the volume of the sphere below O A units 16 3 O B 250 units 48 3 D units C units b
Geometry
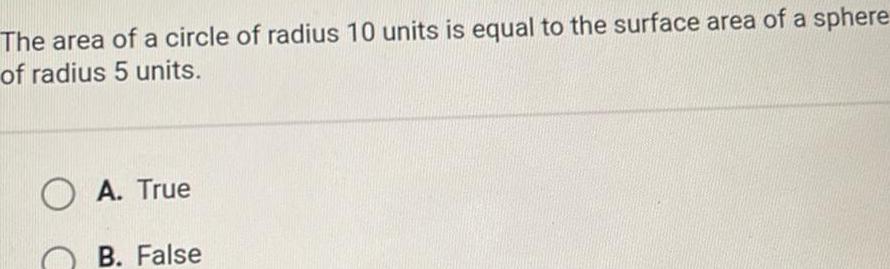
3D GeometryThe area of a circle of radius 10 units is equal to the surface area of a sphere of radius 5 units O A True B False

Geometry
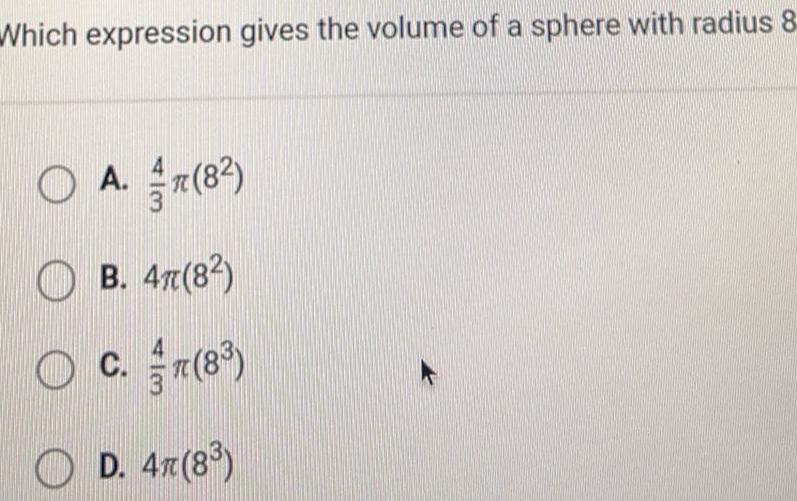
AreaWhat is the volume of a sphere with a radius of 12 units OA 144 units OB 2304 units OC 576 units OD 1728 units
Geometry
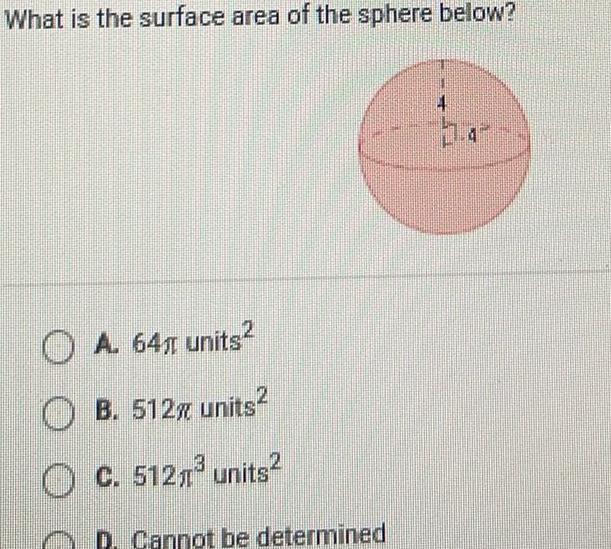
AreaWhat is the surface area of the sphere below O A 64 units B 512 units C 512 units D Cannot be determined 1 47

Geometry
2D GeometryWhat is the surface area of a sphere with a radius of 14 units A 449 units OB 784 units C 784 units OD 288T units
Geometry
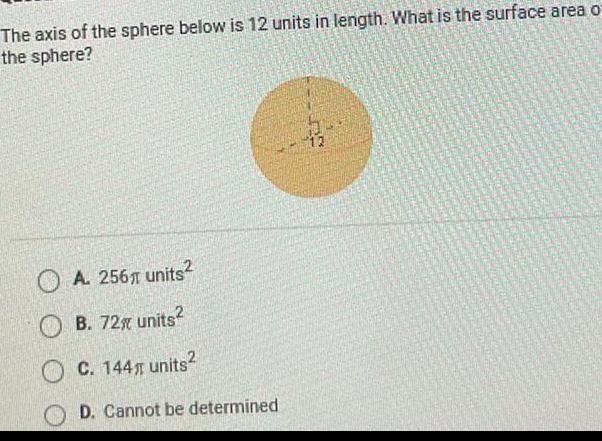
2D GeometryThe axis of the sphere below is 12 units in length What is the surface area of the sphere A 256 units B 72 units C 144 units D Cannot be determined
Geometry
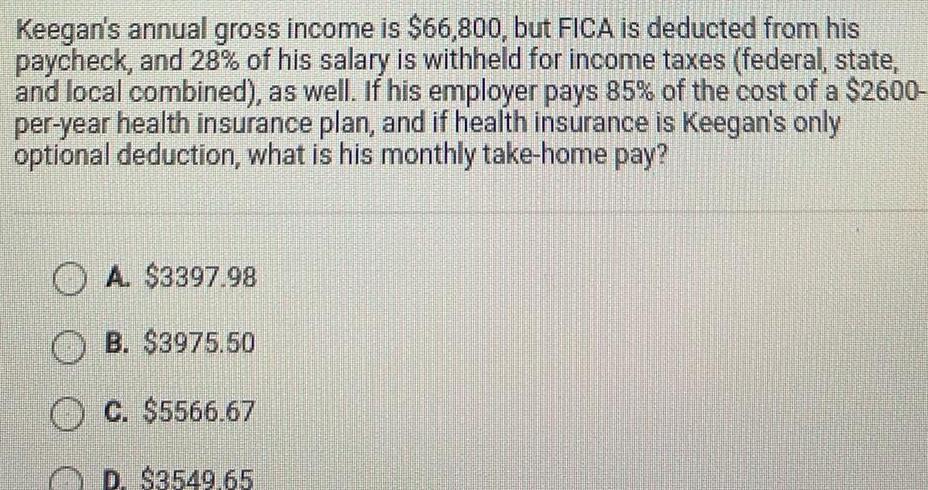
2D GeometryKeegan s annual gross income is 66 800 but FICA is deducted from his paycheck and 28 of his salary is withheld for income taxes federal state and local combined as well If his employer pays 85 of the cost of a 2600 per year health insurance plan and if health insurance is Keegan s only optional deduction what is his monthly take home pay A 3397 98 B 3975 50 C 5566 67 D 3549 65

Geometry
2D GeometryThe cost of 500 000 worth of 15 year term life insurance for Audrey is 28 44 per month If Audrey s employer covers 75 of this cost how much i deducted from Audrey s gross income per year for life insurance A 255 96 B 21 33 C 85 32 D 341 28
Geometry
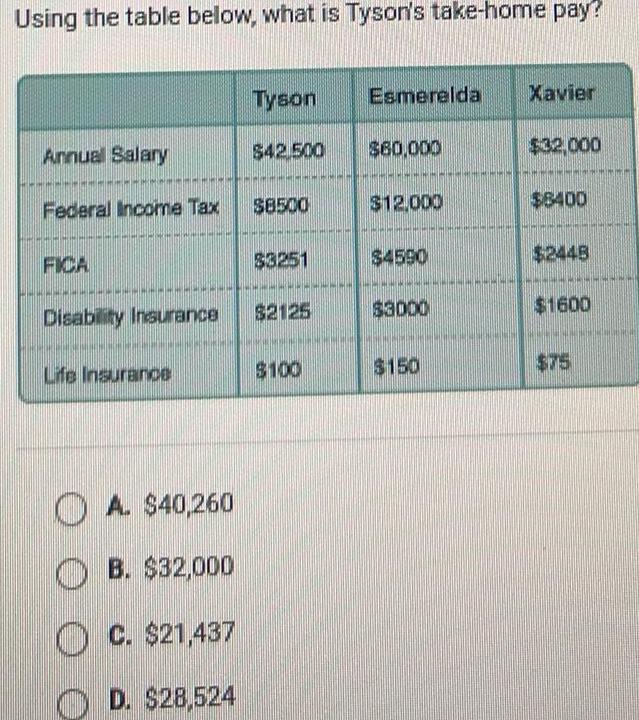
2D GeometryUsing the table below what is Tyson s take home pay Annual Salary Federal Income Tax FICA Disability Insurance Life Insurance A 40 260 B 32 000 O O C 21 437 O D 28 524 Tyson 42 500 8500 3251 2125 100 Esmerelda Xavier 60 000 12 000 4590 3000 150 32 000 6400 2448 1600 75
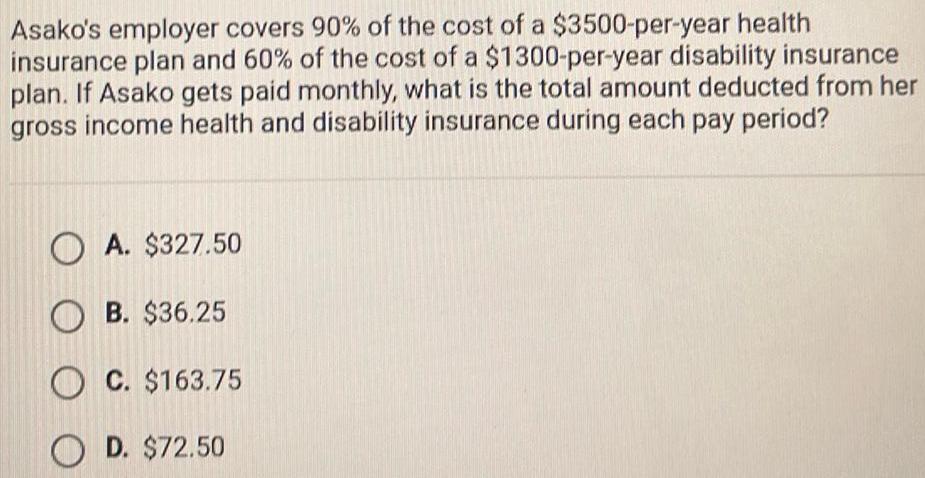
Geometry
2D GeometryAsako s employer covers 90 of the cost of a 3500 per year health insurance plan and 60 of the cost of a 1300 per year disability insurance plan If Asako gets paid monthly what is the total amount deducted from her gross income health and disability insurance during each pay period OA 327 50 OB 36 25 OC 163 75 OD 72 50

Geometry
2D Geometryfield project superintendent earns an annual salary of 72 800 Ontributes 7900 per year to her 401 k plan If she has a required deductio or income taxes federal state and local combined of 28 of pretax come how much does she have withheld in income taxes per year OA 22 120 OB 22 596 OC 18 172 D 20 384
Geometry
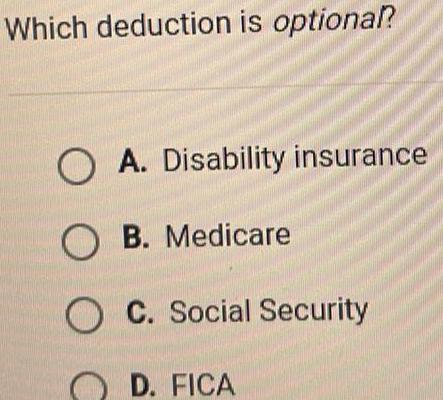
VectorsWhich deduction is optional O A Disability insurance OB Medicare OC Social Security OD FICA
Geometry
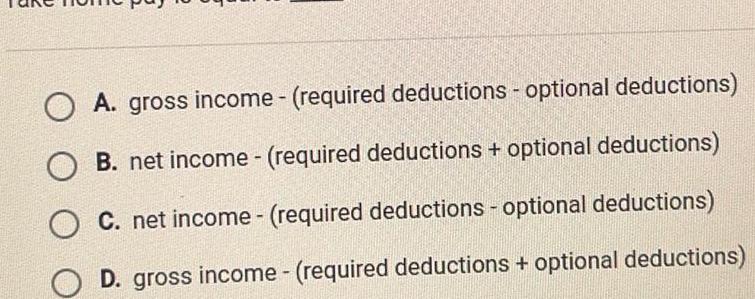
2D GeometryOA gross income required deductions optional deductions B net income required deductions optional deductions C net income required deductions optional deductions D gross income required deductions optional deductions
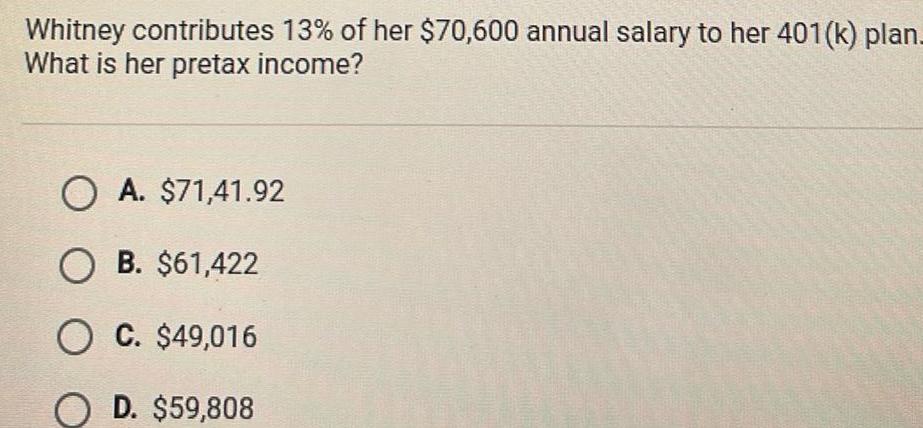
Geometry
2D GeometryWhitney contributes 13 of her 70 600 annual salary to her 401 k plan What is her pretax income O A 71 41 92 O B 61 422 O C 49 016 O D 59 808

Geometry
2D GeometryEli s employer covers 60 of the cost of a 4900 per year health insurance plan and Eli s share of the cost of the plan is his only optional deduction How much is deducted from Eli s paycheck each month for health insurance OA 163 33 OB 167 66 OC 397 00 D 245 00
Geometry
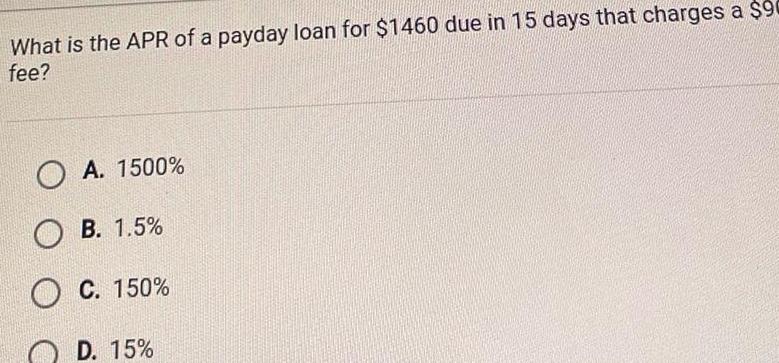
Coordinate systemWhat is the APR of a payday loan for 1460 due in 15 days that charges a 90 fee O A 1500 OB 1 5 O C 150 D 15
Geometry
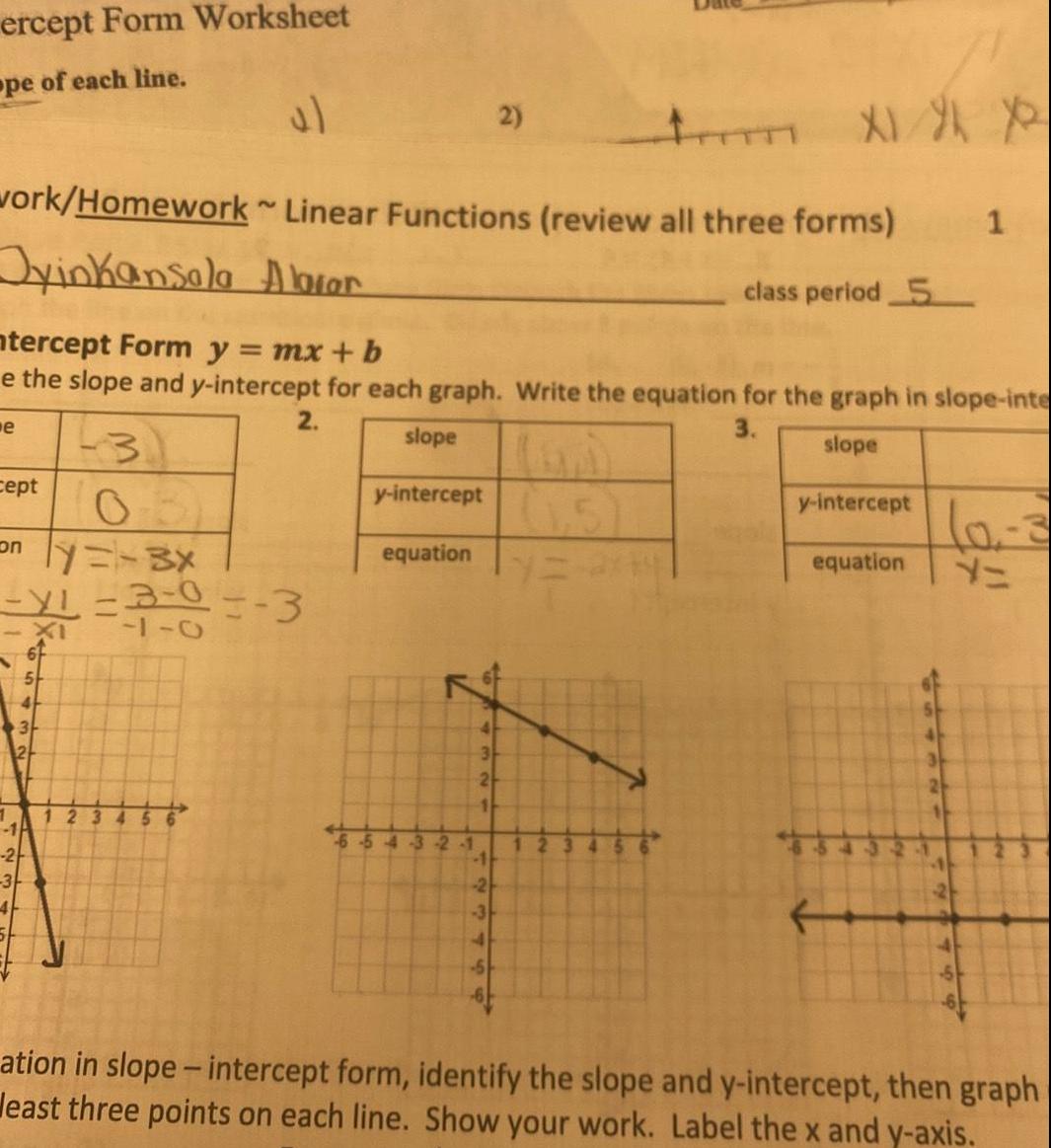
Coordinate systemercept Form Worksheet pe of each line work Homework Linear Functions review all three forms Jyinkansala Abror class period 5 e ntercept Form y mx b e the slope and y intercept for each graph Write the equation for the graph in slope inte 2 3 slope slope 3 y intercept equation cept only 3x XL 3 0 3 1 7 5 XI 4 3 2 y intercept equation 54 3 2 1 2 4 3 24 11 2 3 Im X1 X X 123 3 ation in slope intercept form identify the slope and y intercept then graph least three points on each line Show your work Label the x and y axis

Geometry
Solution of trianglesWhich of these is a correct statement regarding payday loans OA They re easier to get than mortgages but harder to get than car loans B They re easier to get than both mortgages and car loans C They re harder to get than both mortgages and car loans O D They re easier to get than car loans but harder to get than mortgages

Geometry
Solution of trianglesHolly has the option of borrowing 540 for one week at an APR of 700 or borrowing the 540 for one week with a fee of 75 Which is the better deal A Borrowing the 540 for one week with a fee of 75 since Holly will owe less interest this way than with the 700 APR OB Borrowing the 540 for one week with a fee of 75 since Holly will owe more interest this way than with the 700 APR OC Borrowing the 540 for one week at an APR of 700 since Holly will owe more interest this way than with the fee of 75 O D Borrowing the 540 for one week at an APR of 700 since Holly will owe less interest this way than with the fee of 75
Geometry
Areaf a 24 day single payment loan has a periodic interest rate of 8 4 what is the approximate APR of the loan O A 20 2 OB 12 8 O C 127 8 OD 201 6
Geometry
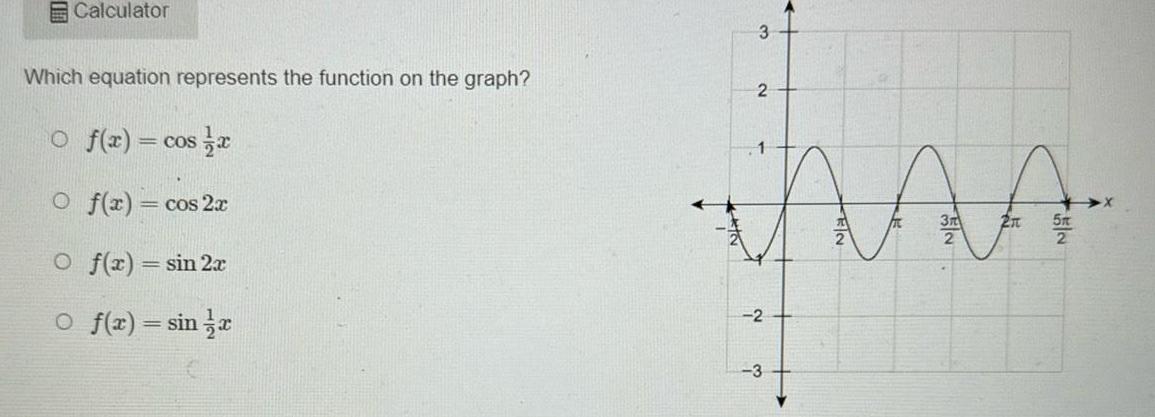
Solution of trianglesCalculator Which equation represents the function on the graph Of x cos x Of x cos2x O f x sin 2x O f x sin r 3 2 inas 2 3
Geometry
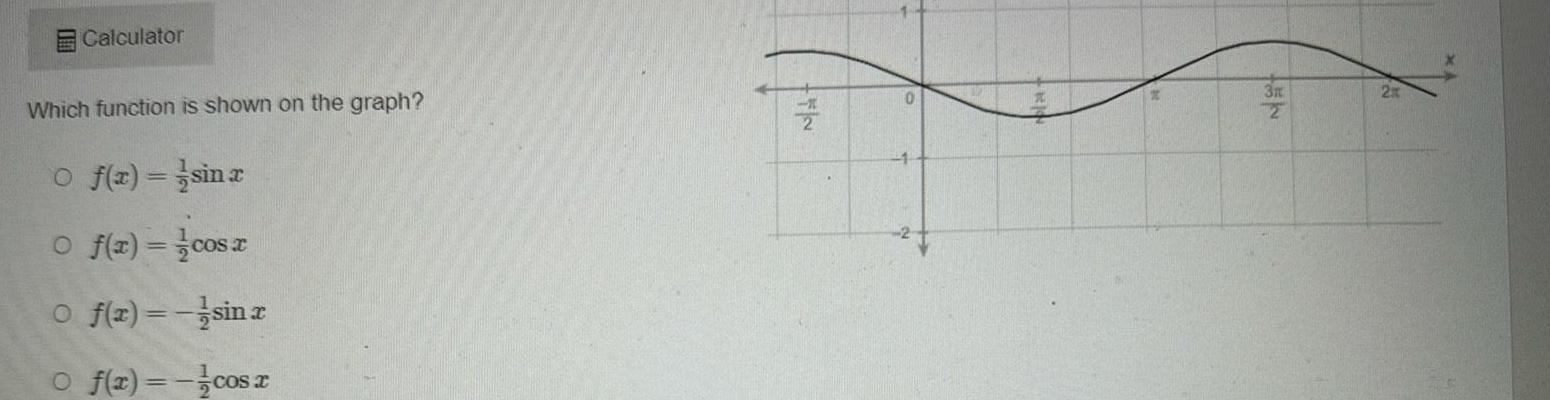
2D GeometryCalculator Which function is shown on the graph Of x sinx O f x cos x O f x sin x O f x cos x 0 3r
Geometry
2D GeometryLacy took out a single payment loan for 610 that charged a 70 fee How much does she have to pay by the time the loan reaches maturity O A 680 O B 70 O C 610 O D 540
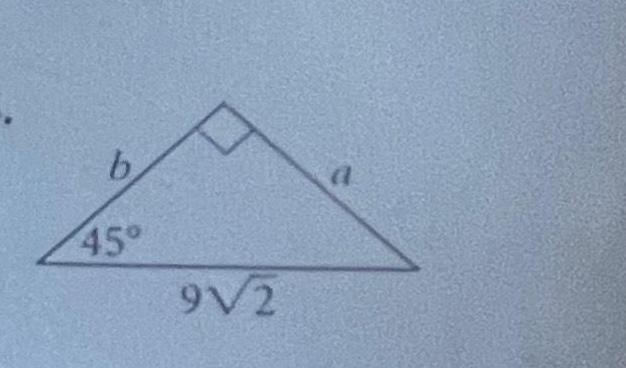
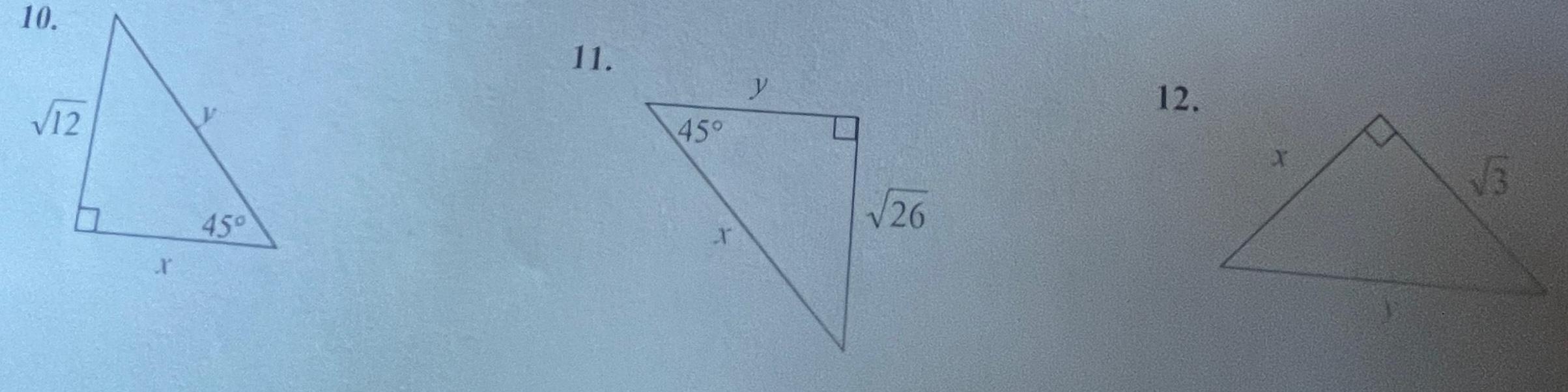
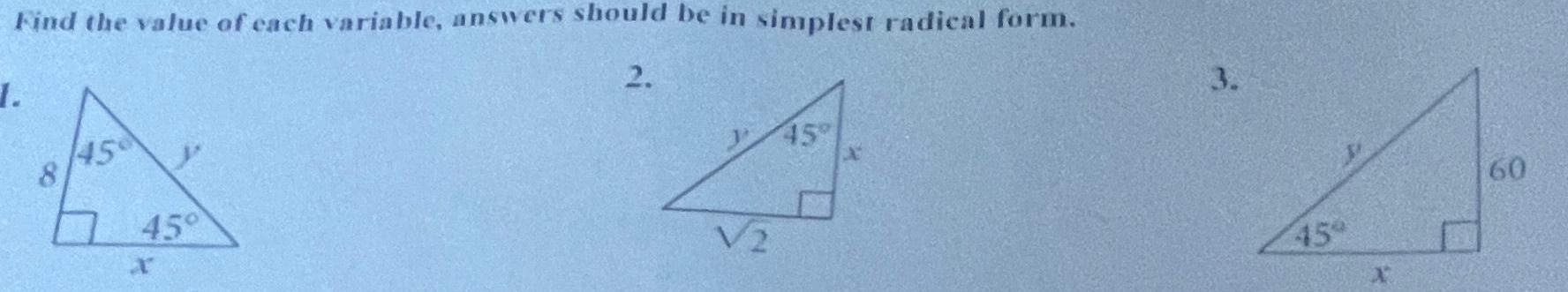
Geometry
2D GeometryFind the value of each variable answers should be in simplest radical form 2 1 45 45 45 3 45 60
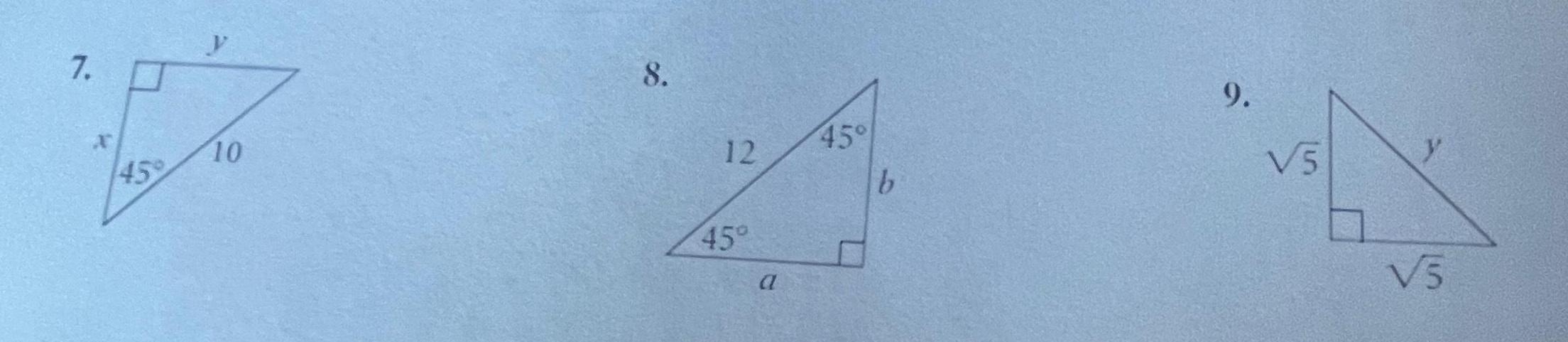

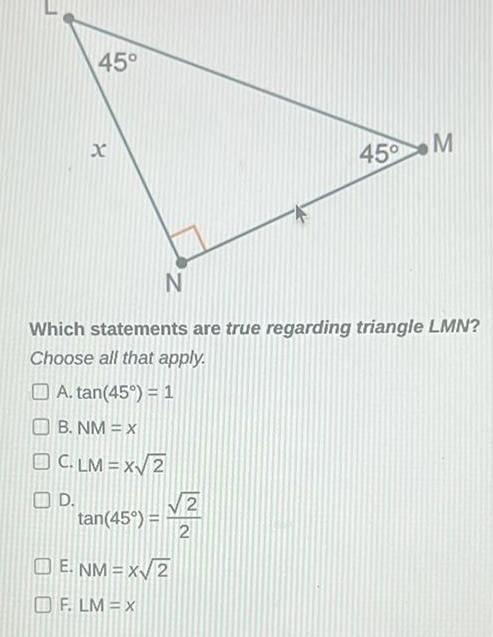
Geometry
2D Geometry45 D X tan 45 N Which statements are true regarding triangle LMN Choose all that apply A tan 45 1 B NM X OC LM x 2 OF LM X 2 2 E NM x 2 45 M
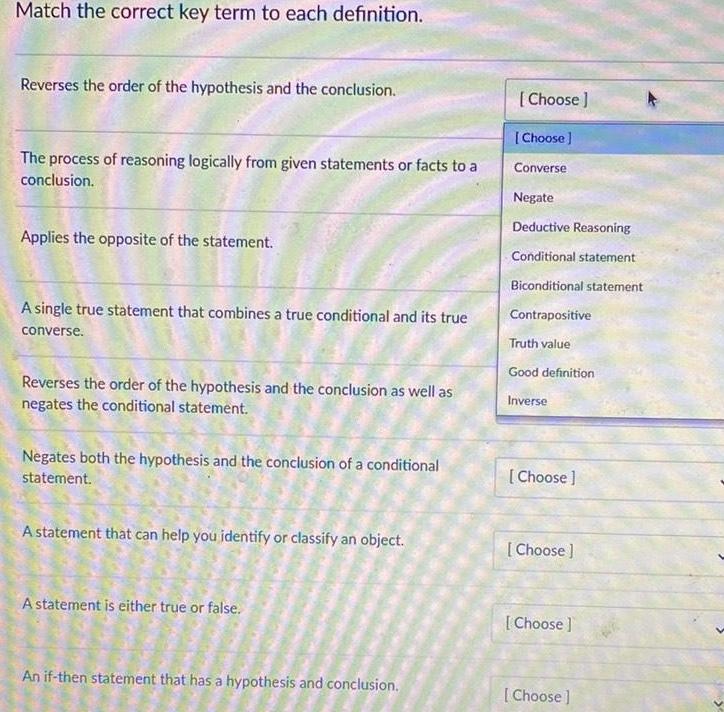
Geometry
VectorsMatch the correct key term to each definition Reverses the order of the hypothesis and the conclusion The process of reasoning logically from given statements or facts to a conclusion Applies the opposite of the statement A single true statement that combines a true conditional and its true converse Reverses the order of the hypothesis and the conclusion as well as negates the conditional statement Negates both the hypothesis and the conclusion of a conditional statement A statement that can help you identify or classify an object A statement is either true or false An if then statement that has a hypothesis and conclusion Choose Choose Converse Negate Deductive Reasoning Conditional statement Biconditional statement Contrapositive Truth value Good definition Inverse Choose Choose Choose Choose
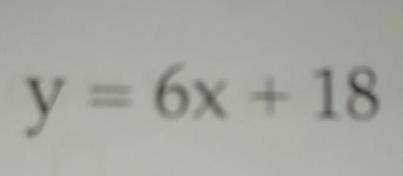
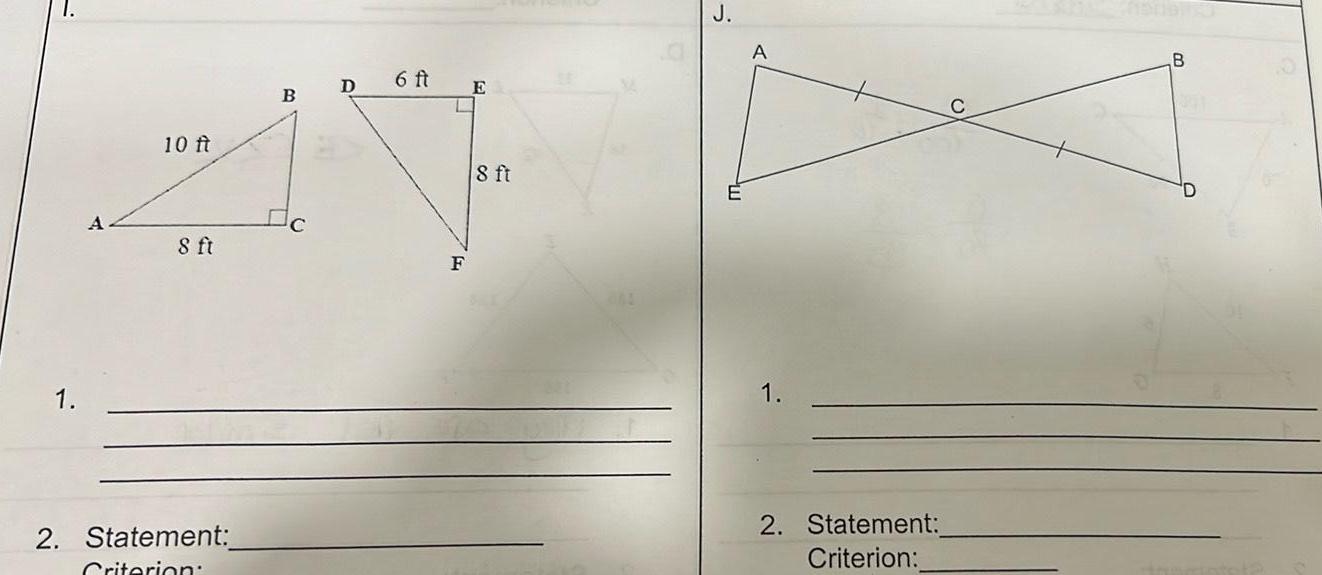
Geometry
2D Geometry1 A 10 ft 8 ft 2 Statement Criterion B D 6 ft F E 8 ft J A 1 2 Statement Criterion B 201
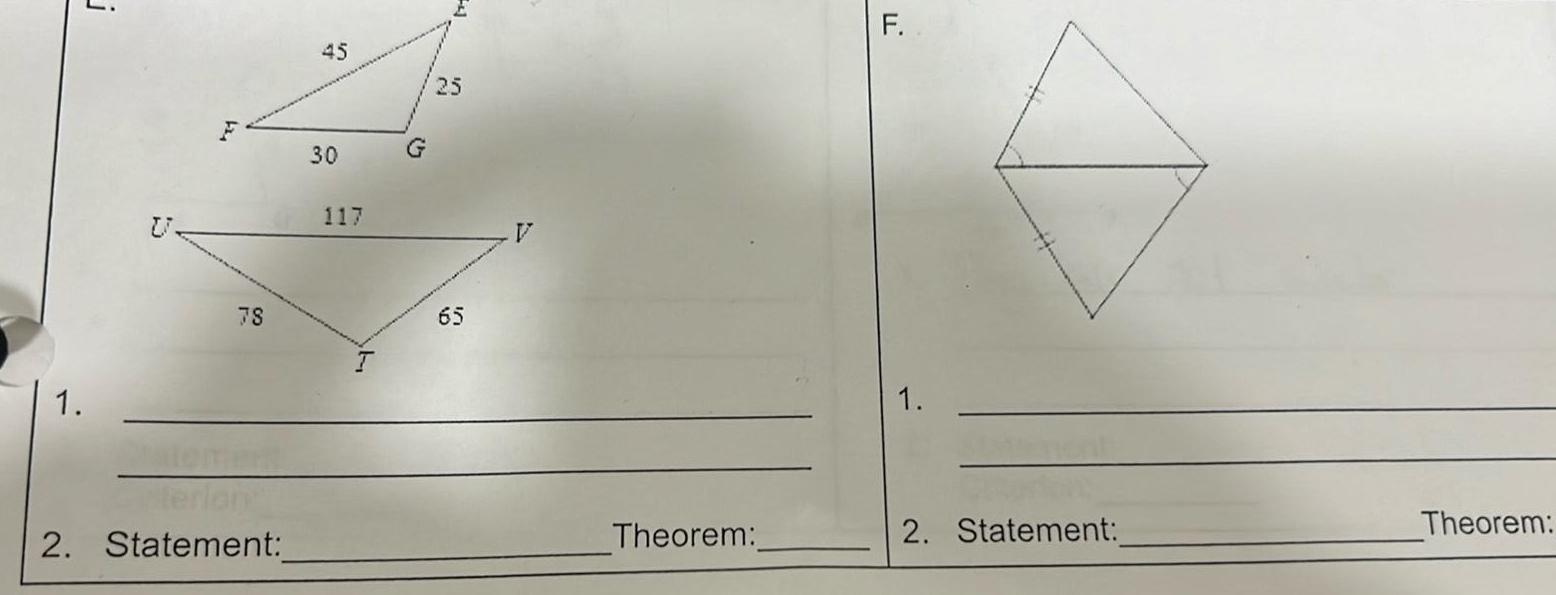
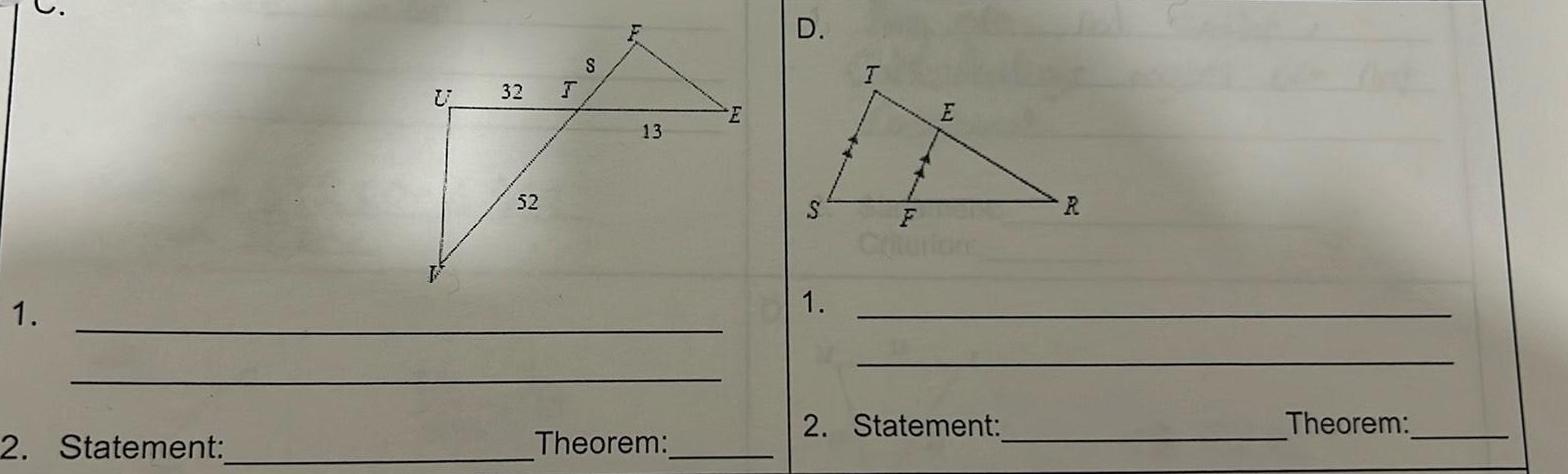
Geometry
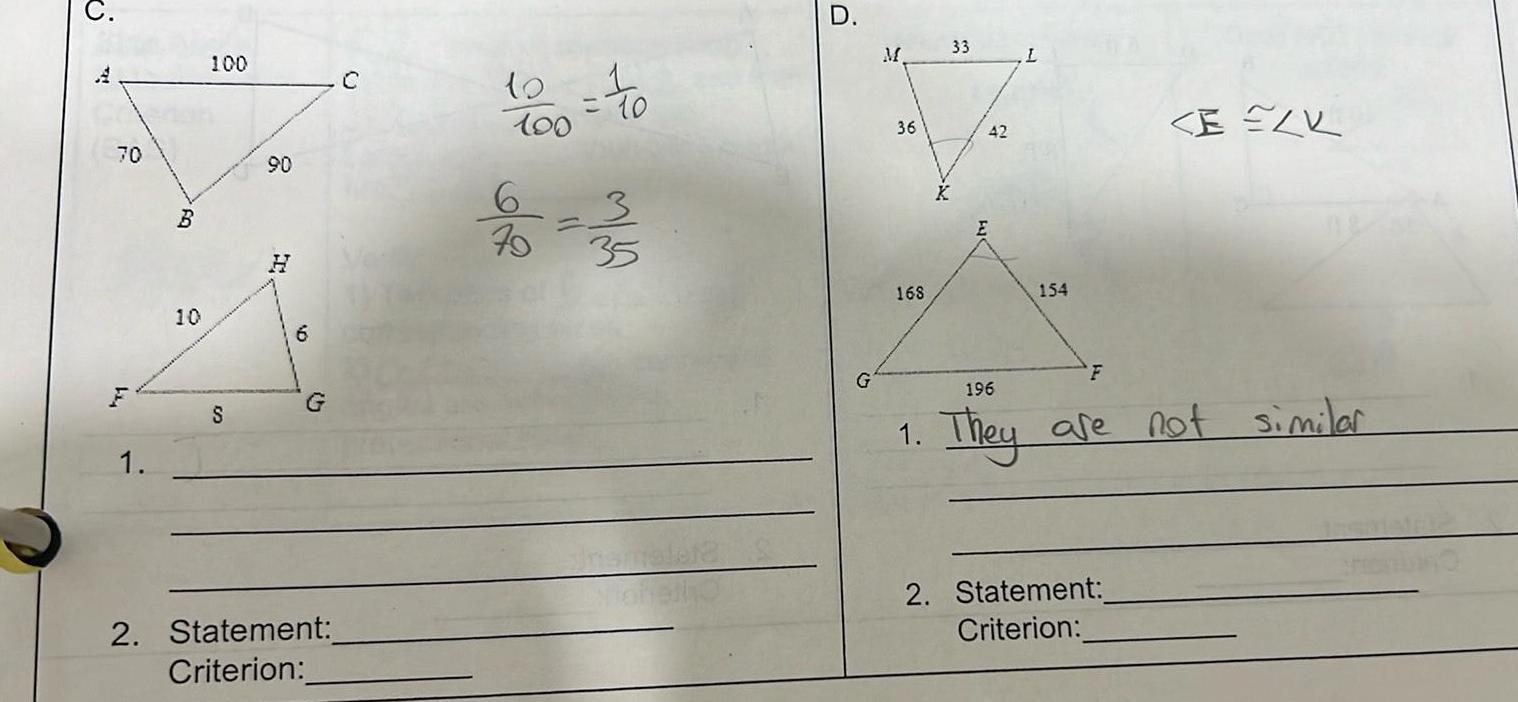
2D Geometry70 FT1 1 by B 10 100 S 90 10 G 2 Statement Criterion C 100 70 1 10 3 35 D G M 36 168 1 33 42 L 154 ELK F 196 They are not similar 2 Statement Criterion

Geometry
Solution of triangles1 2 pair of triangles 1 State one of the following A a b C I know they are similar because I know they are not similar because There is not enough information Statement H Theorem 2 If they ARE similar a b B Write the similarity statement A State the similarity theorem that proves they are similar AA SSS SAS 2 Statement 50 72 G 42 4 66 F 77 Theorem

Geometry
Coordinate systemIn the following problem check that it is appropriate to use the normal approximation to the binomial Then use the normal distribution to estimate the requested probabilities Suppose more than a decade ago high levels of lead in the blood put 89 of children at risk A concerted effort was made to remove lead from the environment Now suppose only 8 of children in the United States are at risk of high blood lead levels LUSE SALT a In a random sample of 202 children taken more than a decade ago what is the probability that 50 or more had high blood lead levels Round your answer to four decimal places X You may have found the complement of the desired probability b In a random sample of 202 children taken now what is the probability that 50 or more have high blood lead levels Round your answer to four decimal places 0 0000

Geometry
2D GeometryGraph the following function over a two period interval Give the period and the amplitude y sin What is the amplitude of the function y sinx Type an integer or a simplified fraction O A 1 5x Which of the following is the correct graph of the function y sin 5x y 25 OB 107 2 Ay 10n O C Ay 10x1 2 X Jox O D Ay X EI
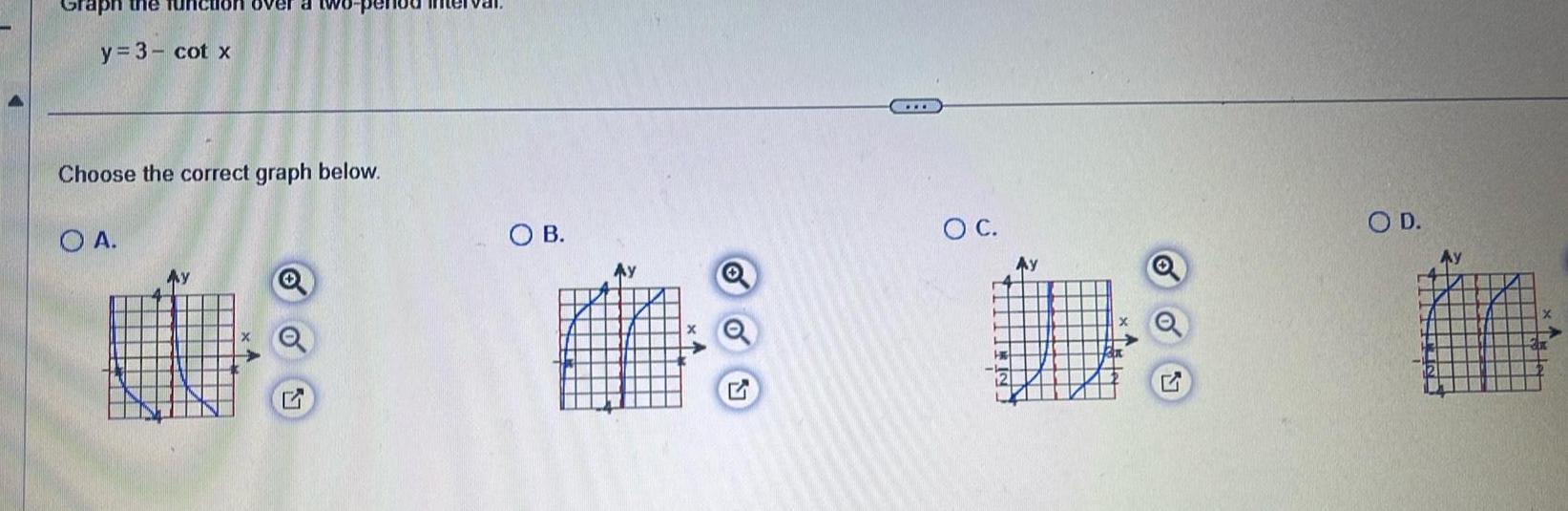
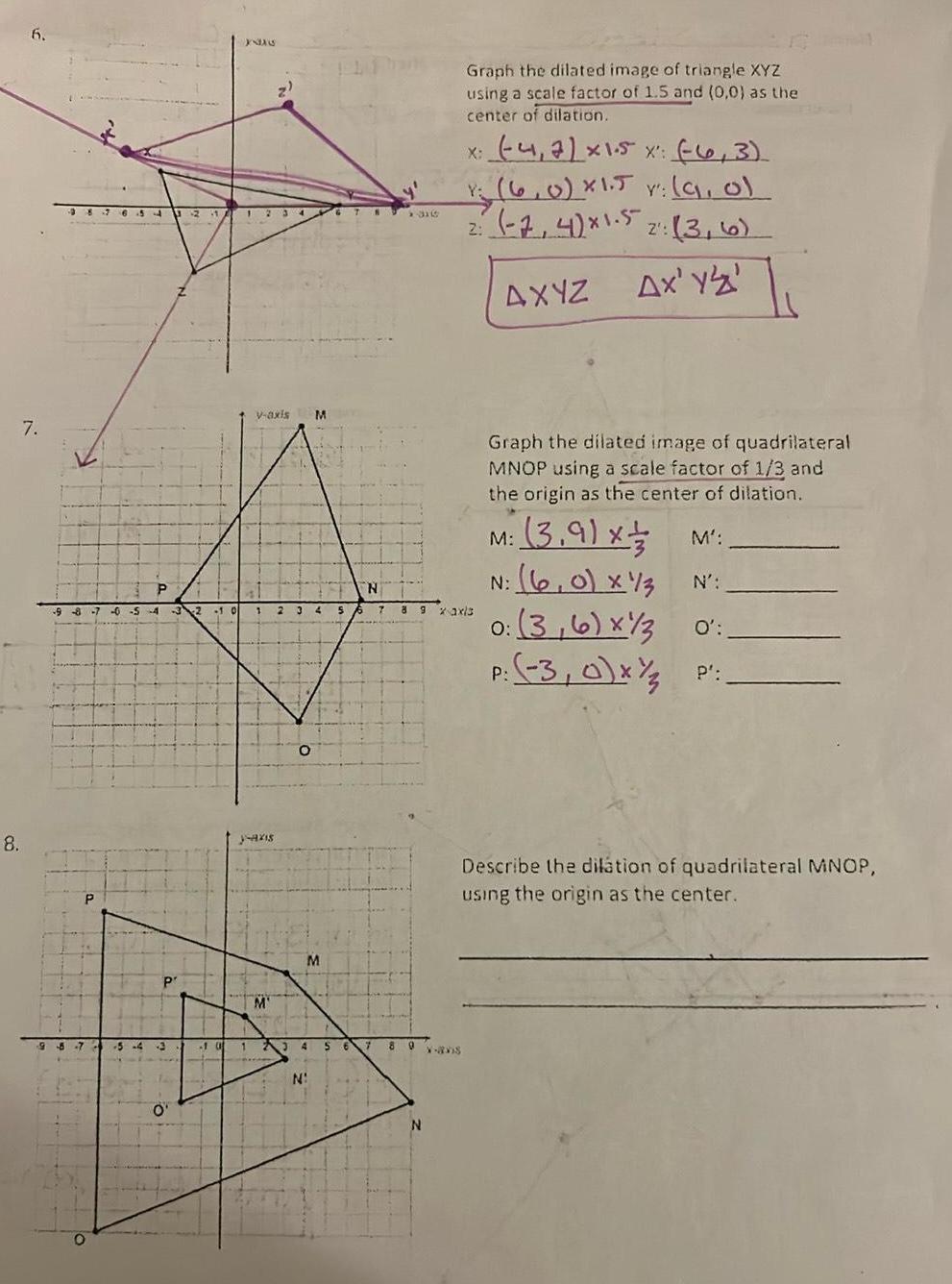
Geometry
2D Geometry6 7 8 8 7 6544 98 7 9 8 7 0 5 4 3 2 1 0 P P 5 4 P O J8A6 21 A 12 V axis M al 1 2 3 4 5 y axis M O M 65 N N 10 123 4 5 6 7 7 1316 8 9 N Graph the dilated image of triangle XYZ using a scale factor of 1 5 and 0 0 as the center of dilation 8 9 xaxis X avis x 4 7 x 1 5 x 6 3 1 6 0 x1 5 v 9 of Y Y 2 7 4 x1 5 2 3 6 2 Ax Y Z AXYZ Graph the dilated image of quadrilateral MNOP using a scale factor of 1 3 and the origin as the center of dilation M 3 9 x N 6 0 x 13 3 6 x 3 O P 3 0 x M N 0 P Describe the dilation of quadrilateral MNOP using the origin as the center
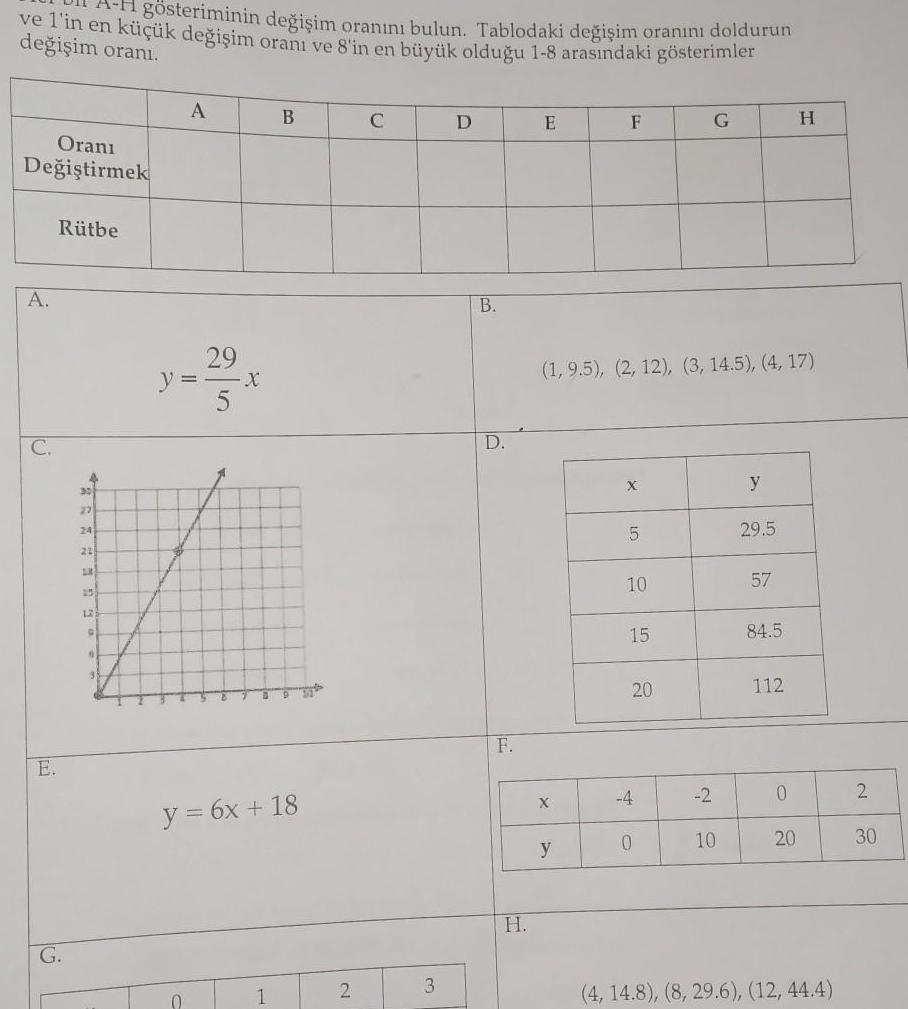
Geometry
Coordinate systemve 1 in en k k de i im oran ve 8 in en b y k oldu u 1 8 aras ndaki g sterimler g steriminin de i im oran n bulun Tablodaki de i im oran n doldurun de i im oran Oran De i tirmek A C E R tbe G 4 30 27 24 23 12 9 6 A 29 y x B y 6x 18 1 2 C 3 D B D F H E X F y 1 9 5 2 12 3 14 5 4 17 X 5 10 15 20 4 0 G 2 10 y 29 5 57 84 5 112 0 H 20 4 14 8 8 29 6 12 44 4 2 30
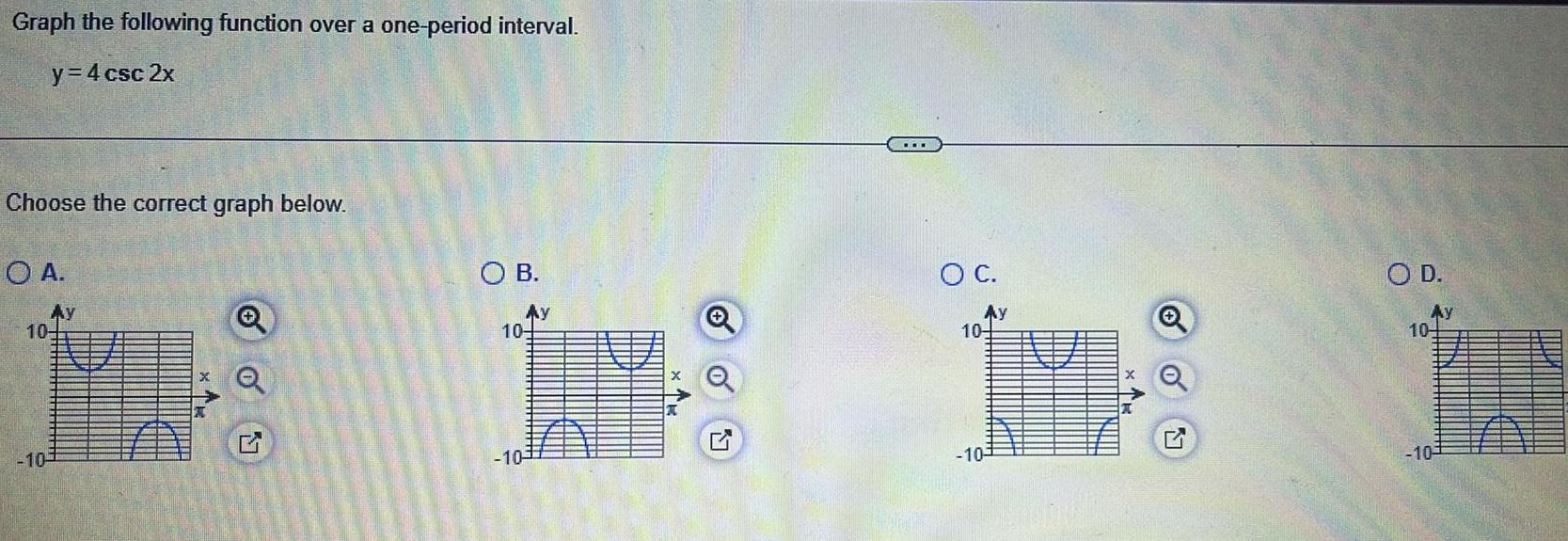
Geometry
VectorsGraph the following function over a one period interval y 4 csc 2x Choose the correct graph below O A AY 10 10 X o Q OB Ay 10 10 O C Ay 104 1 10 AV O D Ay 104 10
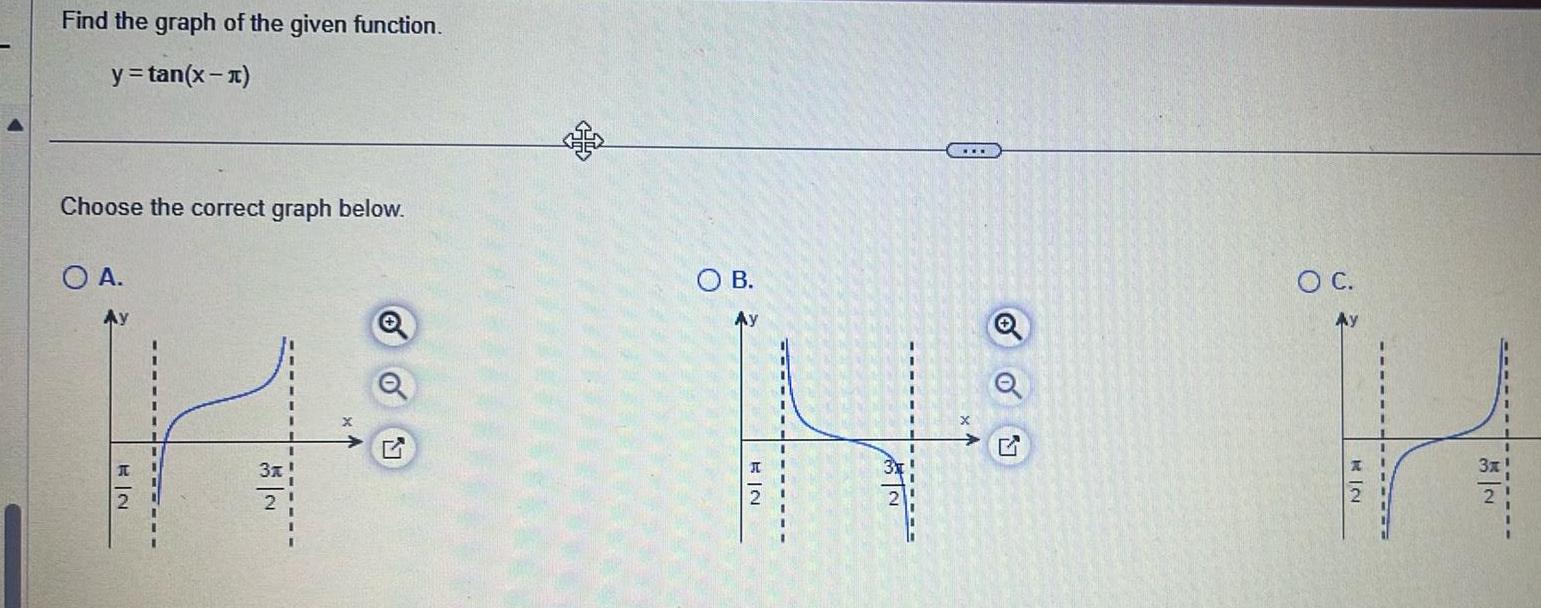
Geometry
2D GeometryFind the graph of the given function y tan x Choose the correct graph below O A Ay EN 3x O B Ay EIN O G O C Ay RIN N
Geometry
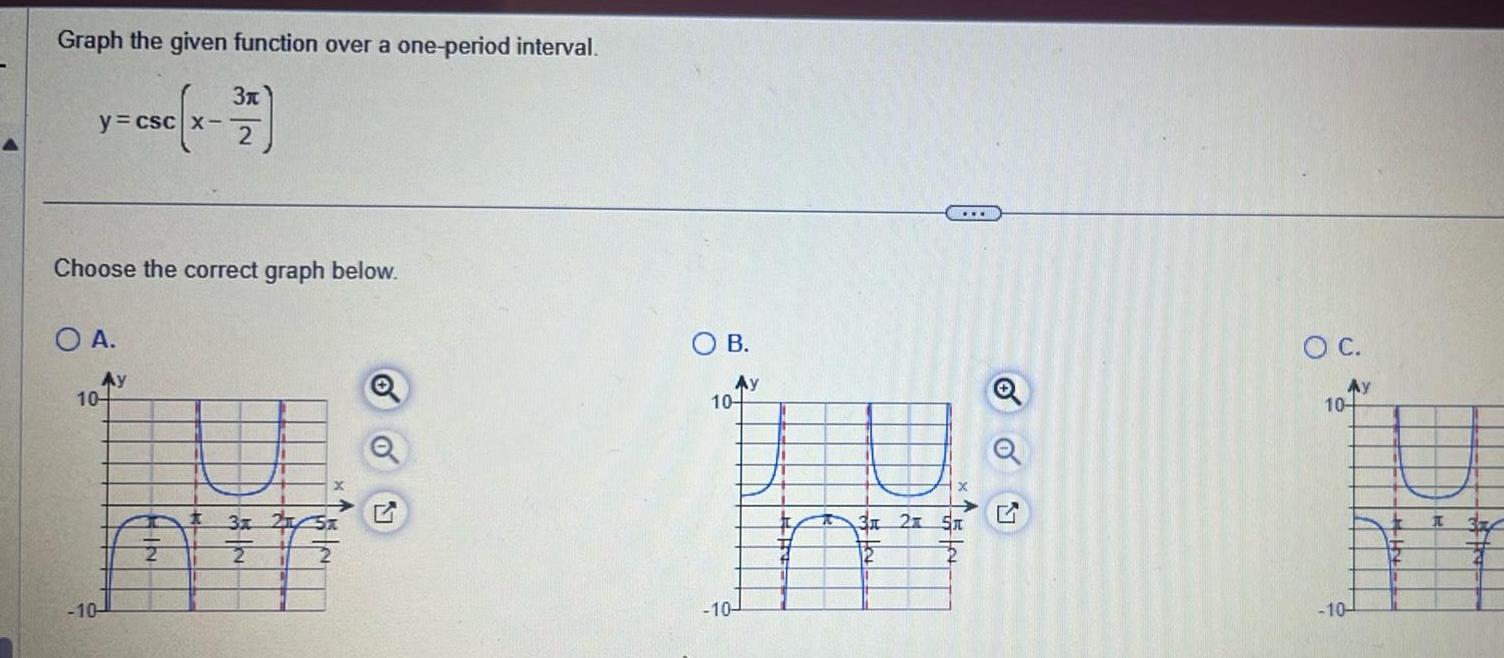
VectorsGraph the given function over a one period interval y csc x 27 Choose the correct graph below O A Ay 10 10 t x 3 215x 2 2 1 A oo OB Ay 10 P 3x 2x 51 T 15 5 10 G O C Ay 10 10 I 3
Geometry
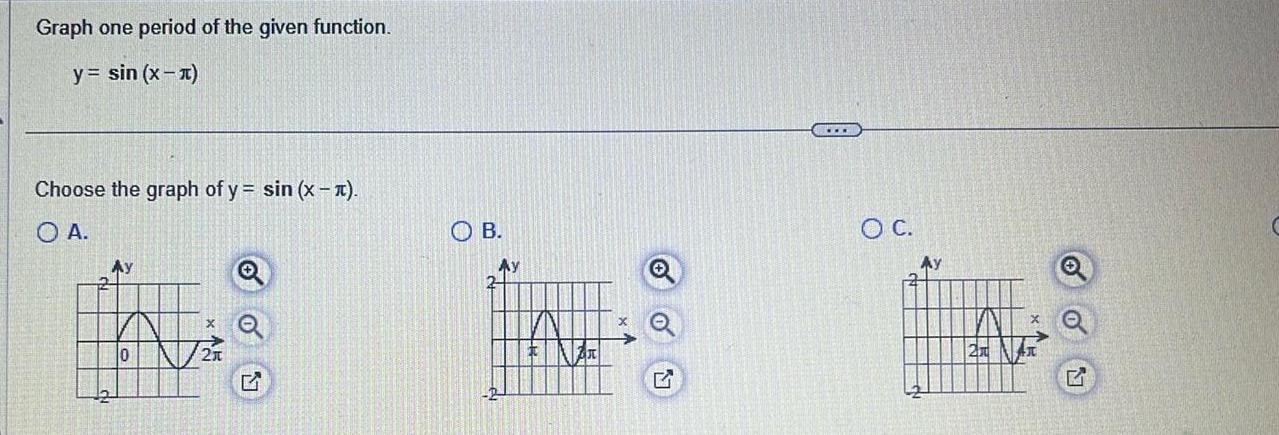
Coordinate systemGraph one period of the given function y sin x x Choose the graph of y sin x x O A 2 Ay n L OB Ay HT S K HKT HTT o o LY www O C Ay H2 Ch 24