Sets and Relations Questions and Answers

Math - Others
Sets and RelationsWrite the domain and the range of the relation. State whether the relation is a function. {(3,6), (4, 6), (5,7), (6,8)}

Math - Others
Sets and RelationsLet the Universal Set, S, have 105 elements. A and B are subsets of S. Set A contains 51 elements and Set B contains 40 elements. If Sets A and B have 27 elements in common, how many elements are in neither A nor B?

Math - Others
Sets and RelationsMoe, Joe, and Hiram are brothers. One day, in some haste, they left home with each one wearing the glasses and scarf of one of the others. Moe was wearing Joe's scarf and Hiram's glasses. Whose glasses and scarf was each one wearing?
Math - Others
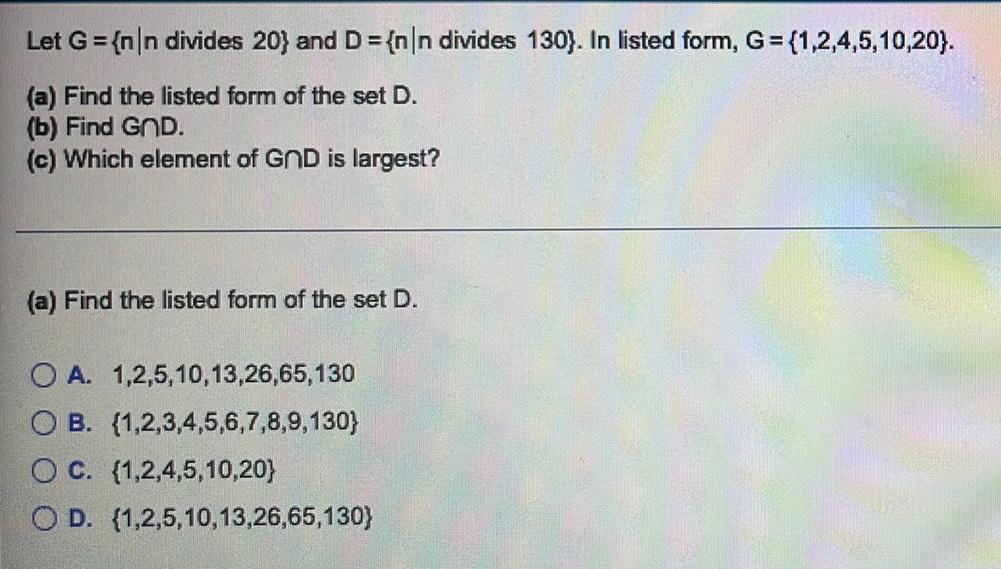
Sets and RelationsLet G = {n|n divides 20} and D = {nn divides 130). In listed form, G = {1,2,4,5,10,20).
(a) Find the listed form of the set D.
(b) Find G⋂D.
(c) Which element of GND is largest?
(a) Find the listed form of the set D.
OA. 1,2,5,10,13,26,65,130
OB. (1,2,3,4,5,6,7,8,9,130)
O C. (1,2,4,5,10,20}
O D. (1,2,5,10,13,26,65,130)
Math - Others
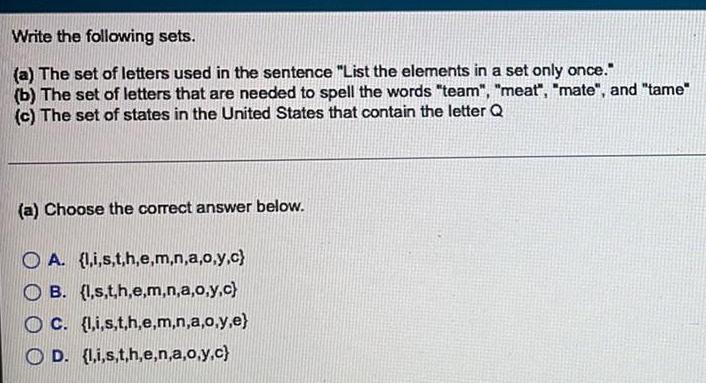
Sets and RelationsWrite the following sets.
(a) The set of letters used in the sentence "List the elements in a set only once."
(b) The set of letters that are needed to spell the words "team", "meat", "mate", and "tame"
(c) The set of states in the United States that contain the letter Q
(a) Choose the correct answer below.
OA. {l,i,s,t,h,e,m,n,a,o,y,c}
OB. {l,s,t,h,e,m,n,a,o,y,c}
OC. {l,i,s,t,h,e,m,n,a,o,y,e}
OD. (l,i,s,t,h,e,n,a,o,y,c}

Math - Others
Sets and RelationsLet U = {1, 2, 3, ..., 1600). Let S be the subset of the numbers in U that are multiples of 4, and let T be the subset of U that are multiples of 9. Since 1600+4=400, it follows that n(S) = n((4-1, 4-2,4-400))=400.
(a) Find n(T) using a method similar to the one that showed that n(S) = 400.
(b) Find n(S⋂T).
(c) Label the number of elements in each region of a two-loop Venn diagram with the universe U and subsets S and T.
(a) Find n(T).

Math - Others
Sets and RelationsDecide whether the following statements asserting set relationships are true or false.
(a) (8,10,12)= {12,10,9}
(b) (10)C(8,10,12}
(c) (5,14,18)= (14,18,5)
(a) Choose the correct answer below.
OA. The statement is false. The sets do not contain the same elements.
OB. The statement is true. The sets contain the same elements.
OC. The statement is false. The two sets list the same elements, but order does matter.
OD. The statement is true. If at least one element is listed in both sets, then the two sets are equal.
Math - Others
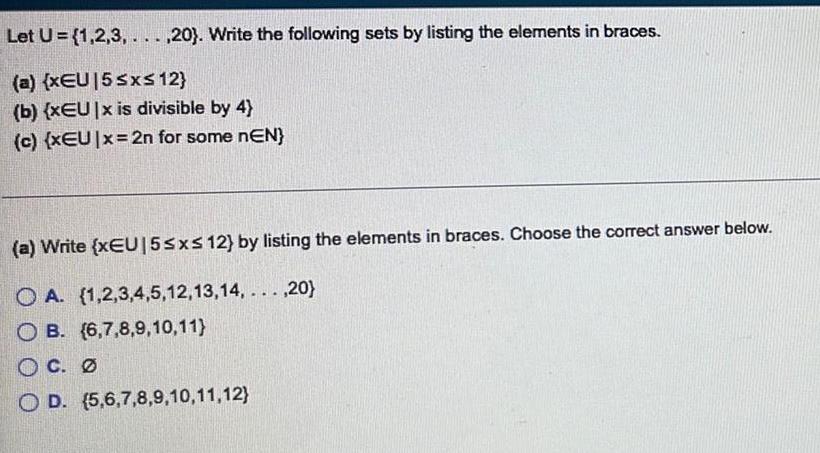
Sets and RelationsLet U={1,2,3,...,20). Write the following sets by listing the elements in braces.
(a) (xEU 15 ≤x≤ 12}
(b) {xEU|x is divisible by 4)
(c) (xEU|x=2n for some nEN}
(a) Write (xEU15≤x≤ 12) by listing the elements in braces. Choose the correct answer below.
OA.
(1,2,3,4,5,12,13,14,...,20)
OB. (6,7,8,9,10,11)
C. Ø
OD. (5,6,7,8,9,10,11,12)

Math - Others
Sets and RelationsFor each part, draw a Venn diagram whose loops for sets A, B, and C show that the conditions listed must hold.
(a) ACC, BCC, ANB=Ø
(b) CC (ANB)
(c) (ANB) CC
Math - Others
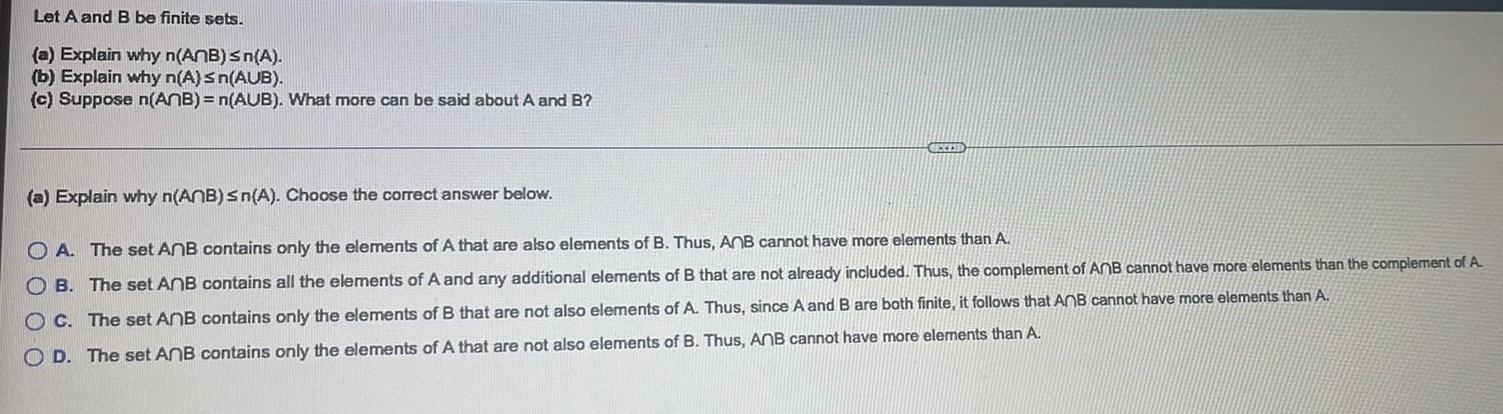
Sets and RelationsLet A and B be finite sets.
(a) Explain why n(ANB) ≤ n(A).
(b) Explain why n(A) ≤n(AUB).
(c) Suppose n(ANB) = n(AUB). What more can be said about A and B?
(a) Explain why n(ANB) ≤n(A). Choose the correct answer below.
OA. The set AnB contains only the elements of A that are also elements of B. Thus, AnB cannot have more elements than A.
OB. The set AnB contains all the elements of A and any additional elements of B that are not already included. Thus, the complement of AnB cannot have more elements than the complement of A.
OC. The set AnB contains only the elements of B that are not also elements of A. Thus, since A and B are both finite, it follows that AnB cannot have more elements than A.
OD. The set AnB contains only the elements of A that are not also elements of B. Thus, AnB cannot have more elements than A.
Math - Others
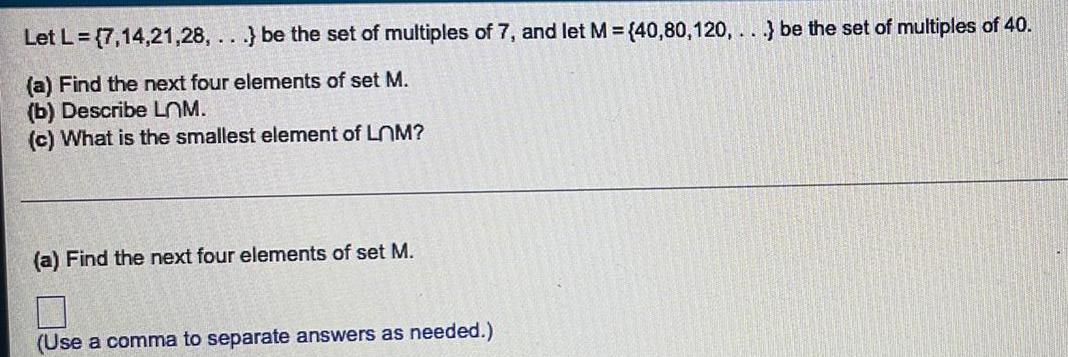
Sets and RelationsLet L = {7,14,21,28,...} be the set of multiples of 7, and let M = {40,80,120,...} be the set of multiples of 40.
(a) Find the next four elements of set M.
(b) Describe LOM.
(c) What is the smallest element of LnM?
(a) Find the next four elements of set M.
(Use a comma to separate answers as needed.)
Math - Others
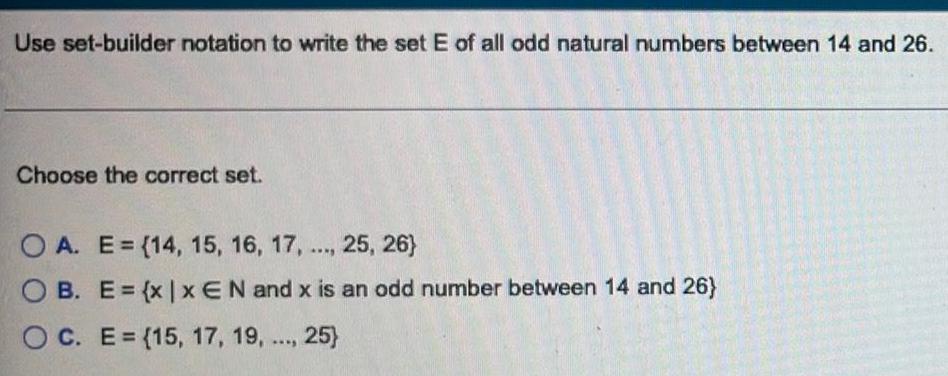
Sets and RelationsUse set-builder notation to write the set E of all odd natural numbers between 14 and 26.
Choose the correct set.
OA. E = (14, 15, 16, 17, ..., 25, 26)
OB. E=(x | xEN and x is an odd number between 14 and 26)
OC. E= {15, 17, 19, ...., 25}

Math - Others
Sets and RelationsLet A, B, and C be finite sets, with ACBCC and n(B) = 11.
(a) What are the possible values of n(A)?
(b) What are the three smallest values of n(C)?

Math - Others
Sets and RelationsIf D⋂F =D⋂G, is it necessarily true that F=G? Explain why or provide a counterexample.
Choose the correct answer below. Use the Show Work learning aid to provide related calculations and additional reasoning to support your answer.
OA. It is not always true.
OB. It is always true.
Math - Others
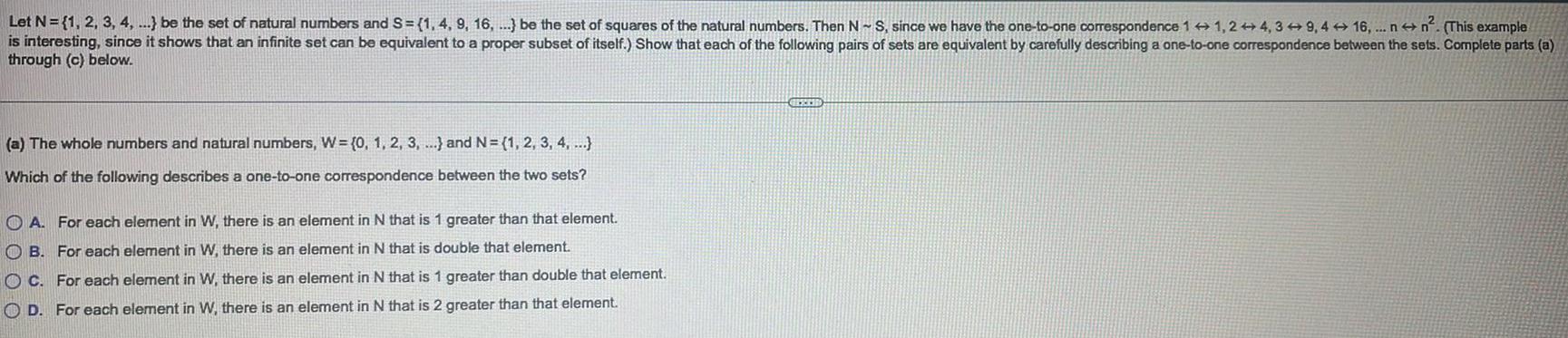
Sets and RelationsLet N = {1, 2, 3, 4, ...} be the set of natural numbers and S= (1, 4, 9, 16, ...) be the set of squares of the natural numbers. Then N - S, since we have the one-to-one correspondence 1+1, 2+4, 39, 416, ... nn². (This example is interesting since it shows that an infinite set can be equivalent to a proper subset of itself.) Show that each of the following pairs of sets are equivalent by carefully describing a one-to-one correspondence between the sets. Complete parts (a) through (c) below.
(a) The whole numbers and natural numbers, W= {0, 1, 2, 3, ...) and N= {1, 2, 3, 4, ...)
Which of the following describes a one-to-one correspondence between the two sets?
A. For each element in W, there is an element in N that is 1 greater than that element.
B. For each element in W, there is an element in N that is double that element.
OC. For each element in W, there is an element in N that is 1 greater than double that element.
D. For each element in W, there is an element in N that is 2 greater than that element.

Math - Others
Sets and RelationsUse counting to determine the whole number that corresponds to the cardinality of these sets.
(a) C = {x|x E N and (x-3)(x-8)=0}
(b) D= (xx EN, 1 sxs 100 and x is divisible by both 4 and 9)
(a) n(C) =
Math - Others
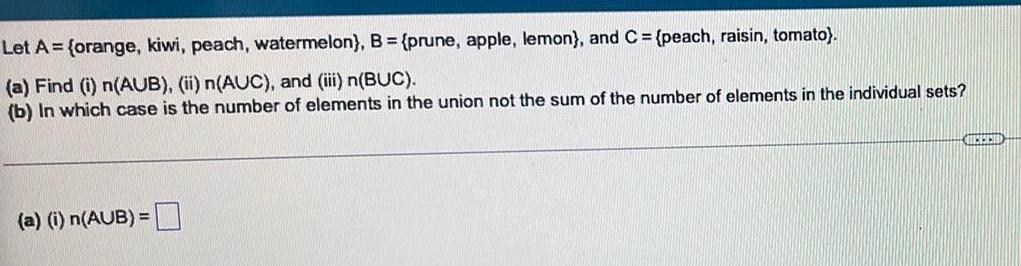
Sets and RelationsLet A = (orange, kiwi, peach, watermelon}, B = {prune, apple, lemon), and C= {peach, raisin, tomato).
(a) Find (i) n(AUB), (ii) n(AUC), and (iii) n(BUC).
(b) In which case is the number of elements in the union not the sum of the number of elements in the individual sets?
(a) (i) n(AUB)=

Math - Others
Sets and RelationsUse the ideas of sets and the definition of the order relation for the whole numbers to justify the transitive property of "less than." That is, if a, b, and c are whole numbers satisfying a <b and b<c, then
OA. Since a<b and b<c, choose sets A, B, C satisfying ACBCC and A = {a}, B = {b), and C= {c}. Since each set has the same cardinality and ACC, it follows that a < c.
B. Since a<b and b<c, choose sets A, B, C satisfying ACBCC and n(A) = a, n(B) = b, and n(C)= c. Since ACBCC, then aEC. n(C) = c and aEC, so a < c.
OC. Since a<b and b<c, choose sets A, B, C satisfying ACBCC and n(A) = a, n(B) = b, and n(C)= c. By the transitive property of set inclusion, ACC, so a < c.
OD. Since a<b and b<c, choose sets A, B, C satisfying ACBCC such that A, B, and C are infinite sets with aEA; a and bEB; and a, b, and CEC. By the definition of set inclusion, it follows that a<c.

Math - Others
Sets and RelationsDetermine which of the following sets are closed under multiplication.
c) {7, 14, 21,...})
e) {0, 1, 7)
d) {7, 9, 11, 13,...}
a) {0, 14)
b) {0}
a) {0, 14) is closed under multiplication.
O False
OTrue

Math - Others
Sets and RelationsThe set C contains 2 and 3 and is closed under addition.
(a) What whole numbers must be in C?
(b) What whole numbers may not be in C?
(c) Are there any whole numbers definitely not in C?

Math - Others
Sets and Relationsere are 62 students in the Travel Club. They discovered that 27 members have visited country A, 30 have visited country B, 28 have been to country C, 9 have visited countries A and B, 11 have been only to country C, and 12 have been only
country A. Some club members have not been to any of the three foreign countries, and, curiously, an equal number have been to all three countries.
How many students have been to all three countries?
How many students have been only to country B?
How many students have been to all three countries?


Math - Others
Sets and Relations1. Find the inverse of the relation {(1, 0), (2, 1), (3, 0), (4, 2)}.
Math - Others
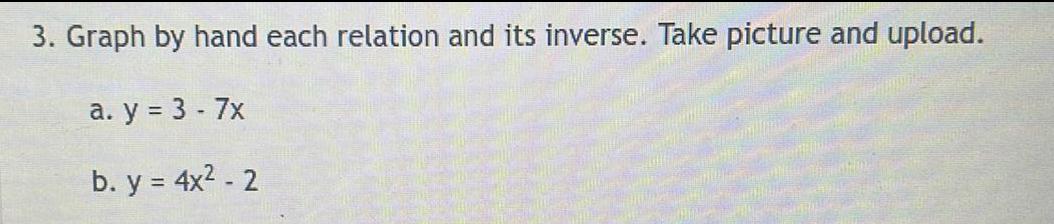
Sets and Relations3. Graph by hand each relation and its inverse. Take picture and upload.
a. y = 3-7x
b. y = 4x² - 2

Math - Others
Sets and Relations1. If A and B are ANY two sets, determine the truth-values of the following statements. If a statement is false, give specific examples of sets A and B that serve as a counter- example
a. (A\B) CA
b. AC (AUB)