Trigonometric equations Questions and Answers
Math - Others
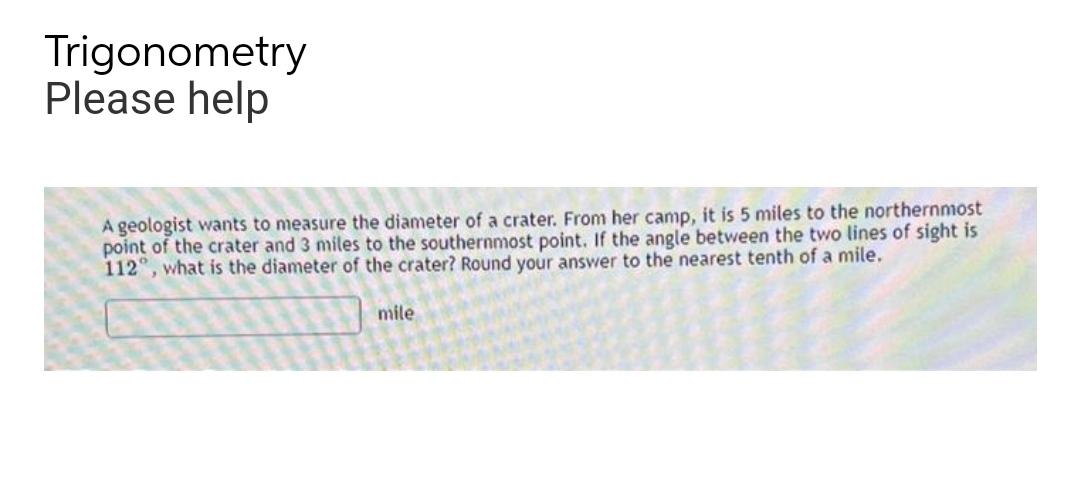
Trigonometric equationsA geologist wants to measure the diameter of a crater. From her camp, it is 5 miles to the northernmost point of the crater and 3 miles to the southernmost point. If the angle between the two lines of sight is 112°, what is the diameter of the crater? Round your answer to the nearest tenth of a mile.
____________mile.

Math - Others
Trigonometric equationsExpress the given sum as a product of sines and/or cosines.
cosx/2 + cos19x/2

Math - Others
Trigonometric equationsSolve these equations algebraically. Find all solutions of each equation on the interval (0,2π). Give exact answers when possible. Round approximate answers to the nearest hundredth.
4 sin^2 x - sin x + 1 = 2 cos^2x


Math - Others
Trigonometric equationsIn which quadrants is tan x = sin x/√(1-sin² x)?
(A) I, II
(B) I, III
(C)I, IV
(D) All Quadrants
Math - Others
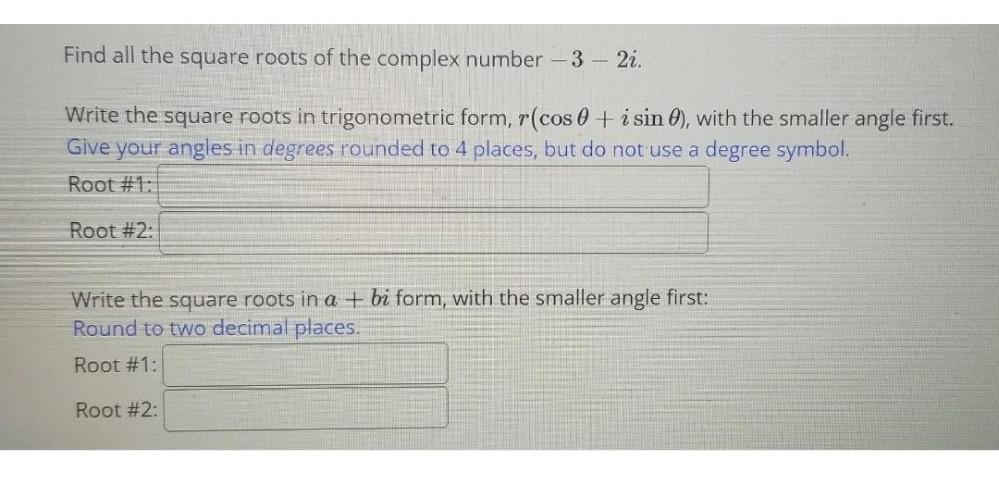
Trigonometric equationsFind all the square roots of the complex number -3 - 2i.
Write the square roots in trigonometric form, r(cosθ+ i sin θ), with the smaller angle first.
Give your angles in degrees rounded to 4 places, but do not use a degree symbol.
Root #1:
Root #2:
Write the square roots in a + bi form, with the smaller angle first:
Round to two decimal places.
Root #1:
Root #2:
Math - Others
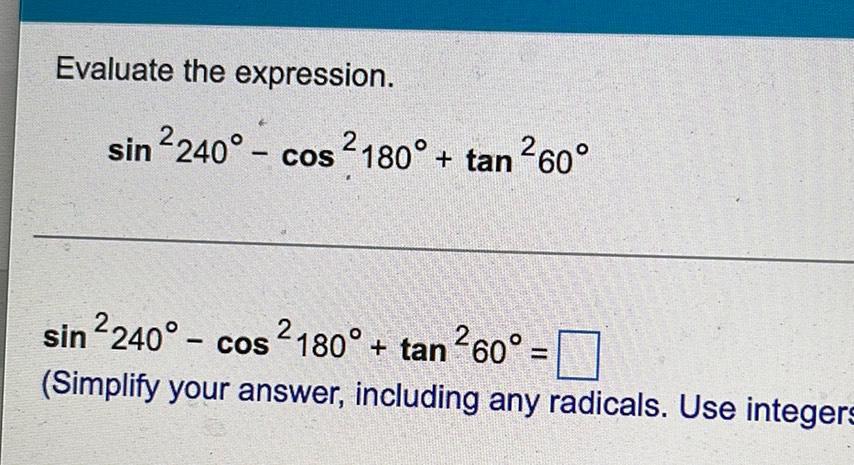
Trigonometric equationsEvaluate the expression.
sin²240° - cos ²180° + tan ²60°=____
(Simplify your answer, including any radicals. Use integers

Math - Others
Trigonometric equationsIf √-4+√8+16 cosec θ + sin θ = (5√3)/6 , where θ lies in 1st quadrant, then tanθ/2 equals
(1) √6
(2) √3
(3)1/(2√3)
(4)1/√3

Math - Others
Trigonometric equationsFind all the complex cube roots of w = 8( cos 210° + i sin 210°). Write the roots in polar form with 0 in degrees.

Math - Others
Trigonometric equationsWrite the following complex number in rectangular form.
14( cos 135°+ i sin 135°)
![Sketch a graph that shows at least one full period. Fill in the table of the "five important points" using the method shown in the notes:
y=-1+cos [2(x-π/4)]](https://media.kunduz.com/media/sug-question/raw/81127490-1659551917.0709965.jpeg?w=256)
Math - Others
Trigonometric equationsSketch a graph that shows at least one full period. Fill in the table of the "five important points" using the method shown in the notes:
y=-1+cos [2(x-π/4)]
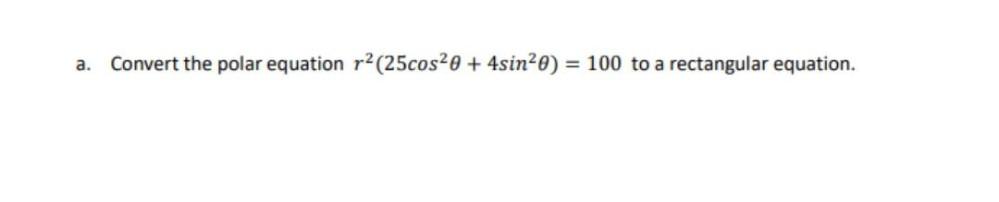
Math - Others
Trigonometric equationsConvert the polar equation r² (25cos²θ + 4sin²θ) =100 to a rectangular equation.
Math - Others
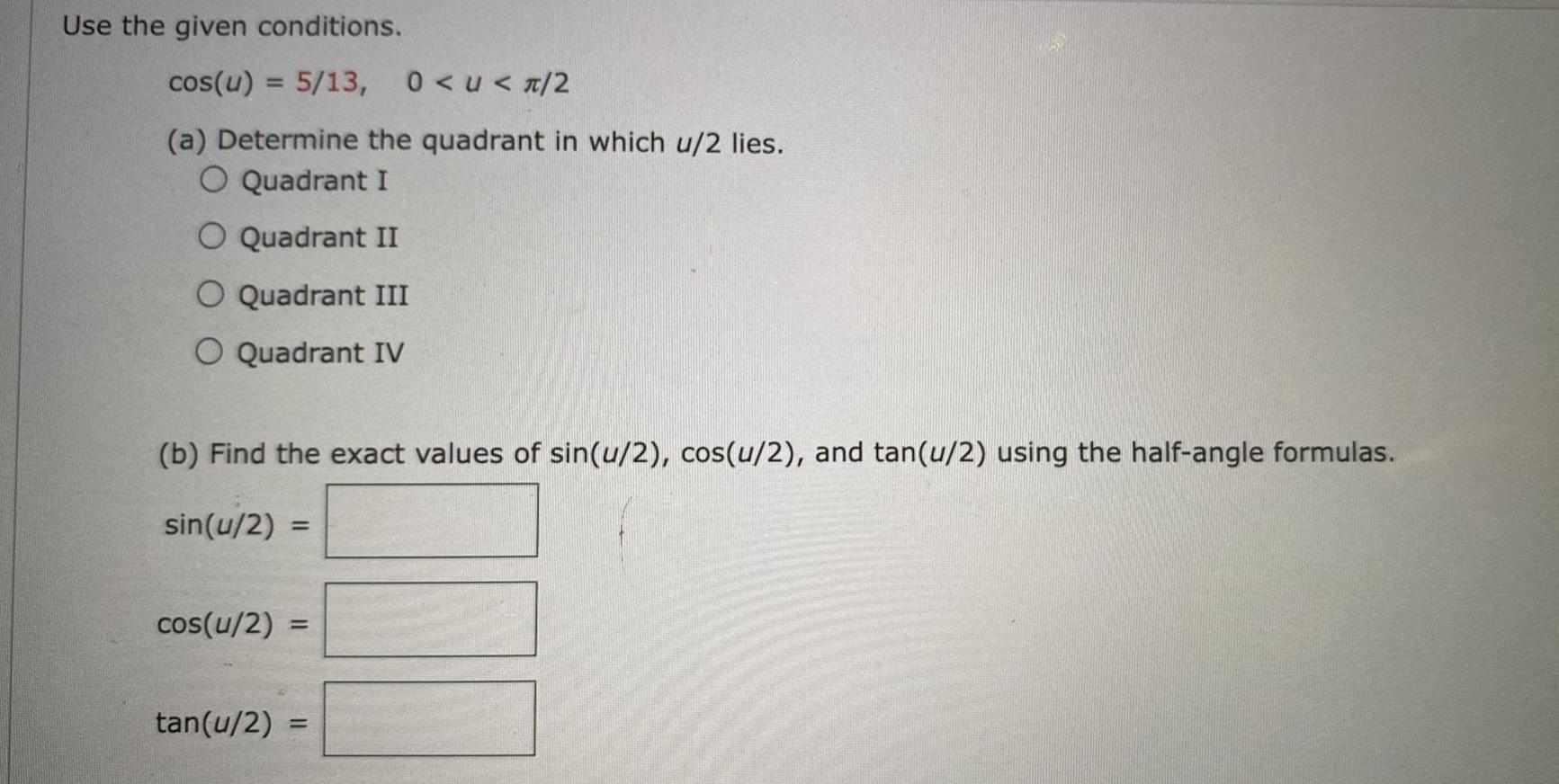
Trigonometric equationsUse the given conditions.
cos(u) = 5/13, 0<u<π/2
(a) Determine the quadrant in which u/2 lies.
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
(b) Find the exact values of sin(u/2), cos(u/2), and tan(u/2) using the half-angle formulas.
sin(u/2)=
cos(u/2) =
tan(u/2)=
Math - Others
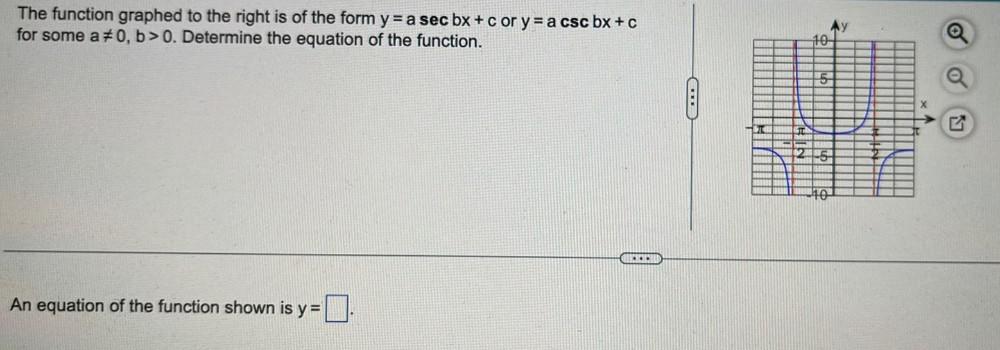
Trigonometric equationsThe function graphed to the right is of the form y = a sec bx + c or y = a csc bx + c for some a ≠ 0, b>0. Determine the equation of the function.
An equation of the function shown is y =

Math - Others
Trigonometric equationsGiven the equation y = 3+2sin(2x-π) Identify the following: 1) amplitude, 2) period 3) phase shift and 4) give the coordinates of at least 5 key points.
Amplitude =
Period =

Math - Others
Trigonometric equationsThe domain of both the sine and cosine functions is ___, and the range is ____.
(Type your answers in interval notation. Type exact answers, using π as needed.)
Math - Others
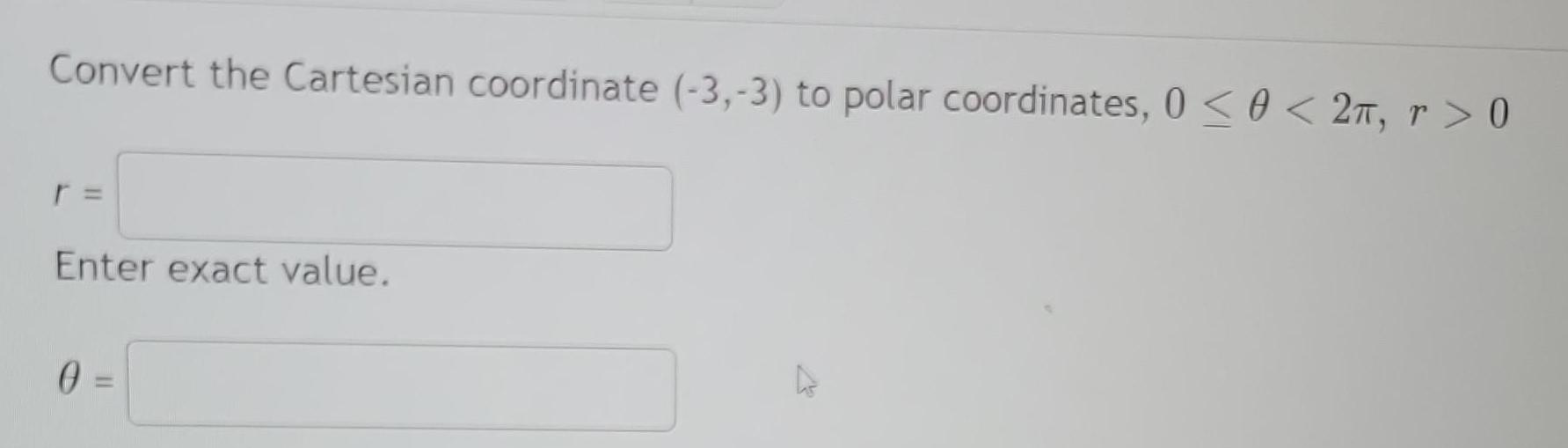
Trigonometric equationsConvert the Cartesian coordinate (-3,-3) to polar coordinates, 0≤ θ < 2π, r> 0
r=
Enter exact value.
θ=

Math - Others
Trigonometric equationsFind all real numbers that satisfy the equation. Round approximate answers to the nearest hundredth.
2 sin(πx) =
Group of answer choices
{x|x = 0.33 + 2k or x = 0.67 + 2k}
{x|x = 0.33 + k or x = 1.67 + k}
{x|x = 0.17 + 2k or x = 0.83 + 2k}
{x|x = 0.33 + k or x = 0.67 + k}
![[11] Solve for the variable over C. Circle answers in r cis θ form.
-168 + 3x³ = 2019](https://media.kunduz.com/media/sug-question/raw/84731731-1659210643.8303816.jpeg?w=256)
Math - Others
Trigonometric equations[11] Solve for the variable over C. Circle answers in r cis θ form.
-168 + 3x³ = 2019
Math - Others
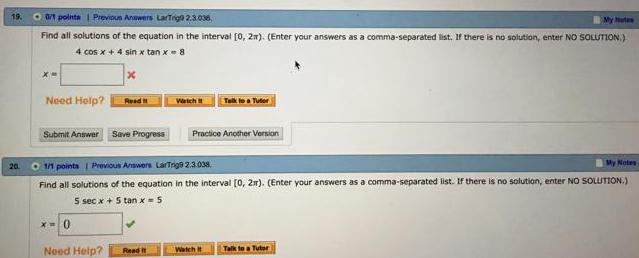
Trigonometric equationsFind all solutions of the equation in the interval [0, 2π). (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION.)
4 cos x + 4 sin x tan x = 8
X=
Find all solutions of the equation in the interval [0, 2r). (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION.)
5 sec x + 5 tan x = 5
X=

Math - Others
Trigonometric equationsAn equivalent expression to cos(θ ) tan(θ ) is:
a) sin(θ)
b)1/cos (θ )
c) 2 sin(θ) cos(θ)
d) tan(θ )

Math - Others
Trigonometric equationsFor which of the following is there no solution for x?
a) sin(x) - 3 = 0
b) sin(x) = 0.5
c) sin(x) = -0.5
d) sin(x) - 1 = 0
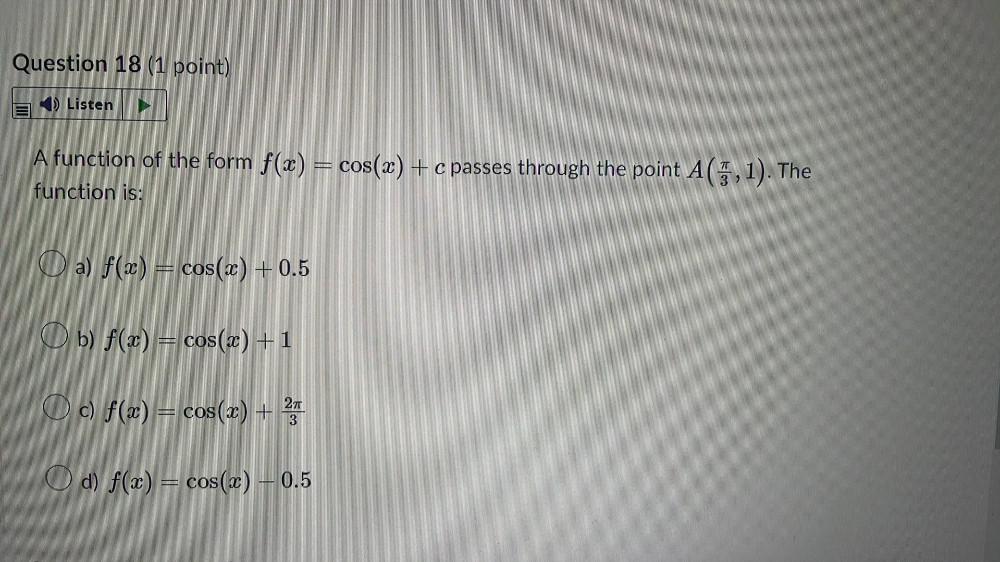
Math - Others
Trigonometric equationsA function of the form f(x) = cos(x) + c passes through the point A(π/3, 1). The
function is:
a) f(x) = cos(x) +0.5
b) f(x) = cos(x) + 1
c) f(x) = cos(x) + 2π/3
d) f(x) = cos(x) – 0.5

Math - Others
Trigonometric equationsIn a small fishing village outside of St. John's, Newfoundland, the tides can be modeled by the function: H(t) = 2.5 cos 2π(t - 3)/12 + 4 With H(t) measured in metres and t measured in hours after midnight. When will
the tide height be 2.5 m (for the first time)?
a) just after 7 am
b) 16.3 days
c) just after 7 days
d) the tide will never be this height

Math - Others
Trigonometric equationsTo calculate the height of a tower Mary measures the angle of elevation from a point A, to be 100. She then walks directly towards the tower, and finds the angle of elevation from the new point B to be 200. What is the height of the tower to the nearest tenth of a meter? Show all your work.
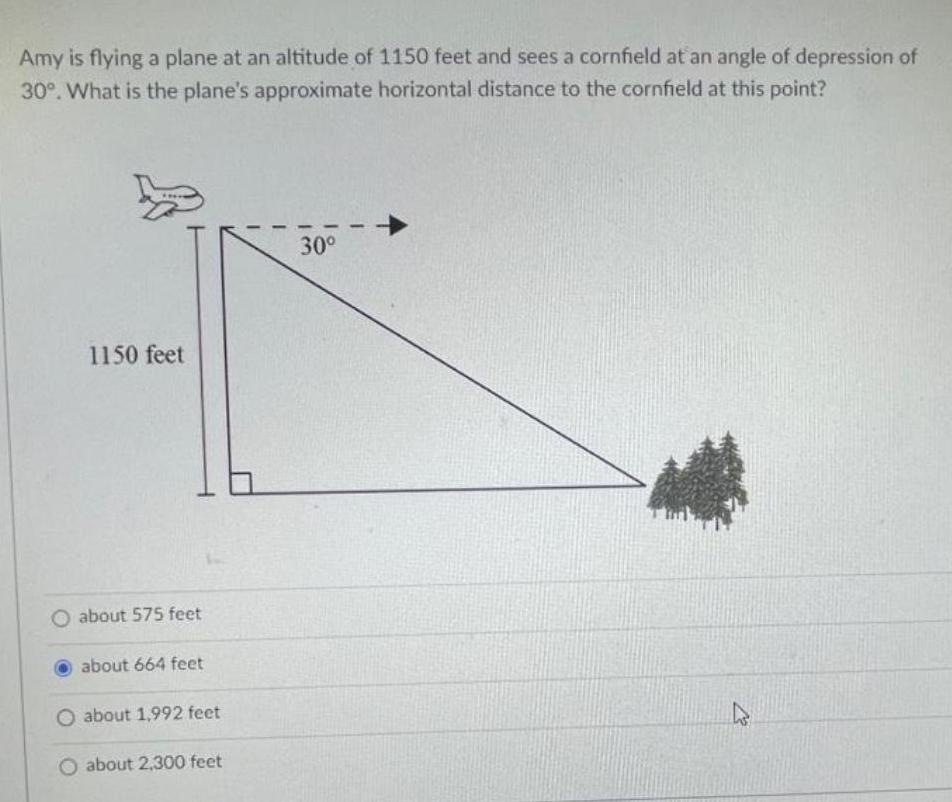
Math - Others
Trigonometric equationsAmy is flying a plane at an altitude of 1150 feet and sees a cornfield at an angle of depression of
30°. What is the plane's approximate horizontal distance to the cornfield at this point?

Math - Others
Trigonometric equationsProve the following trig identities. Show all of your steps for full marks.
a) sec θcos θ + sec θ sinθ = 1 + tan θ
b) sin² x +sin x cos x/tan x = 1

Math - Others
Trigonometric equationsUsing the Law of Sines to solve the all possible triangles if A -
If no answer exists, enter DNE for all answers.
ZB is 31
x
degrees
ZC is 29
x degrees
C = 18
120°, a
32, 6 = 19.
Assume A is opposite side a, ZB is opposite side b, and ≤0 is opposite side c.


Math - Others
Trigonometric equationsUse the product-to-sum identities to rewrite the following expression as a sum or difference.
4sin (3π/4) cos (3π/4)

Math - Others
Trigonometric equationsUse the sum and difference identities to determine the exact value of the following expression. If the answer is undefined, write DNE.
sin 165 cos75 - cos165 sin75

Math - Others
Trigonometric equationsfor sin 2x + Cas x = 0, Use a double angle or
half angle formula to simplify the equation
and then find all solutions of equation
in interval [0, 2π).
x₁ =
x2=
X3²
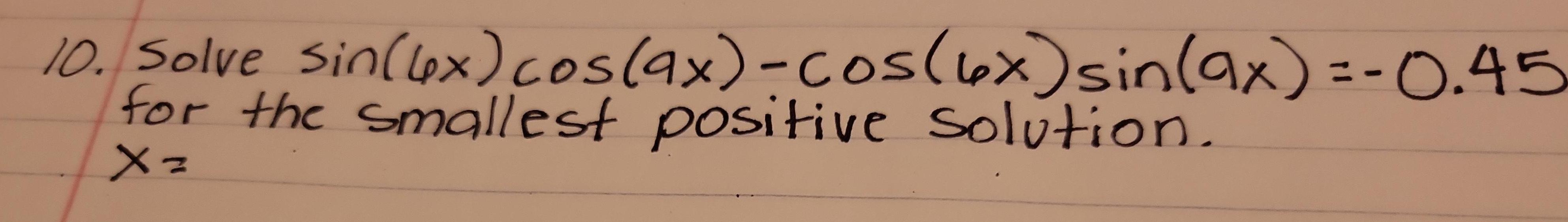
Math - Others
Trigonometric equationsSolve sin(4x) cos(9x) - cos(6x) sin(9x) = -0.45 for the smallest positive solution. X =
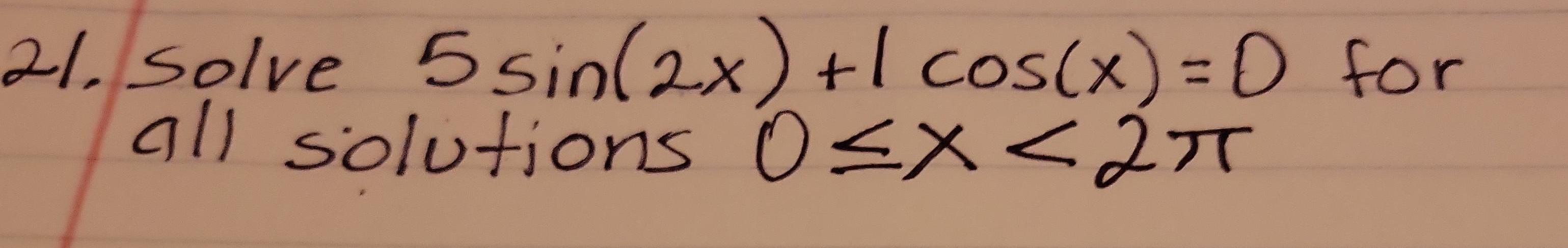
![Q: The range of the function f(x) = log√13,
(5 sin ( (π/3)+ x) +12 sin ((5π/6)+x))) is
a) (0,2]
b) (-∞, 2]
c) (-∞, 1/2]
d) (0, 1/2]](https://media.kunduz.com/media/sug-question/raw/84640350-1658667510.8083835.jpeg?w=256)
Math - Others
Trigonometric equationsQ: The range of the function f(x) = log√13,
(5 sin ( (π/3)+ x) +12 sin ((5π/6)+x))) is
a) (0,2]
b) (-∞, 2]
c) (-∞, 1/2]
d) (0, 1/2]
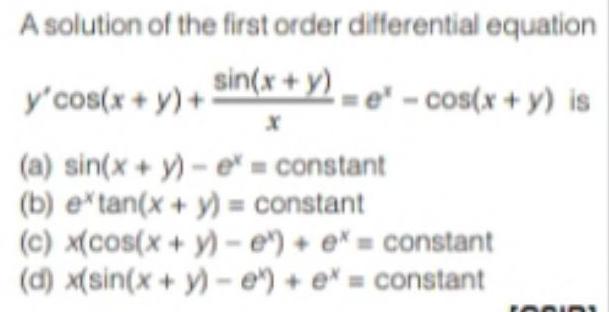
Math - Others
Trigonometric equationsA solution of the first order differential equation
y'cos(x+y)+ sin(x+y)/x=e^x-cos(x + y) is
(a) sin(x + y)- e^x = constant
(b) e^xxtan(x + y) = constant
(c) x(cos(x + y)-e^x) + e^x = constant
(d) x(sin(x + y) -e^x) + e^x = constant


Math - Others
Trigonometric equationsSolve 2 cos² (w) + cos(w) - 1 = 0 for all solutions 0 ≤w < 2.
<
W=
Give your answers as exact values in a list separated by commas.
Math - Others
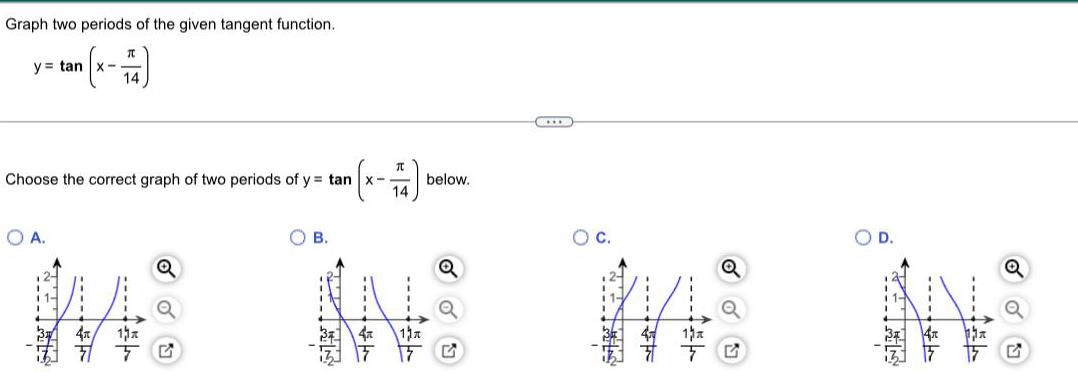
Trigonometric equationsGraph two periods of the given tangent function. (x- π / 14 ) y = tan Choose the correct graph of two periods of y= tan ( x- π / 14 )

Math - Others
Trigonometric equationsA boat leaves the entrance to a harbor and travels 175 miles on a bearing of N 54° E. How many miles north and how many miles east from the harbor has the boat traveled?
Math - Others
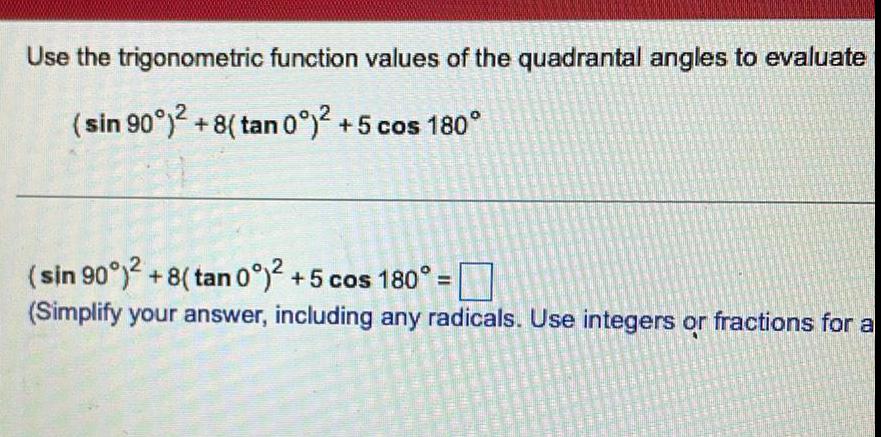
Trigonometric equationsUse the trigonometric function values of the quadrantal angles to evaluate
(sin 90°)² +8( tan 0°)² +5 cos 180°
(sin 90°)² + 8( tan 0°)² +5 cos 180° =
(Simplify your answer, including any radicals. Use integers or fractions for a
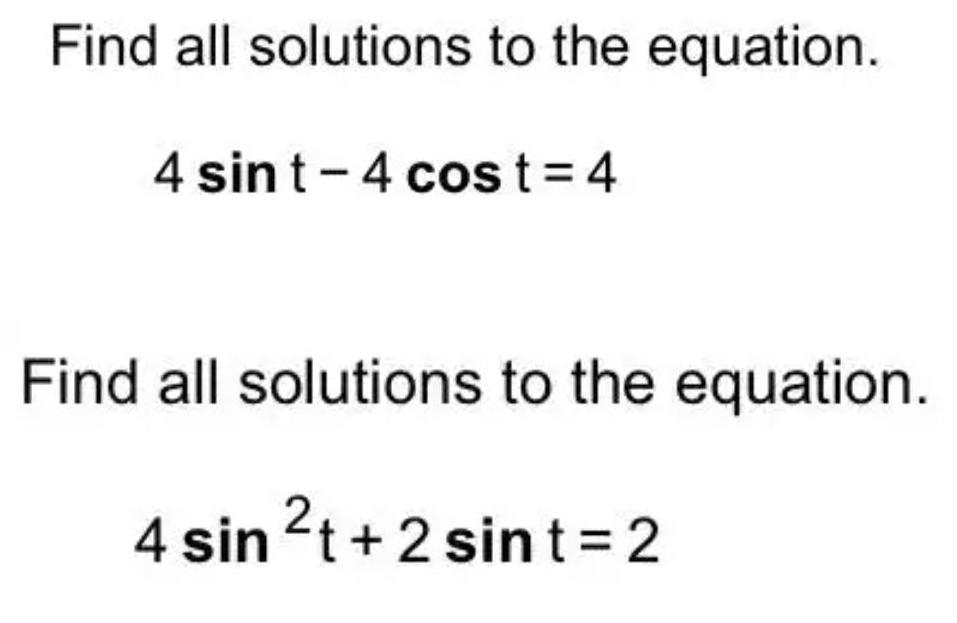
Math - Others
Trigonometric equationsFind all solutions to the equation.
4sint-4cost=4
Find all solutions to the equation.
4sin ²t+2sint=2
Math - Others
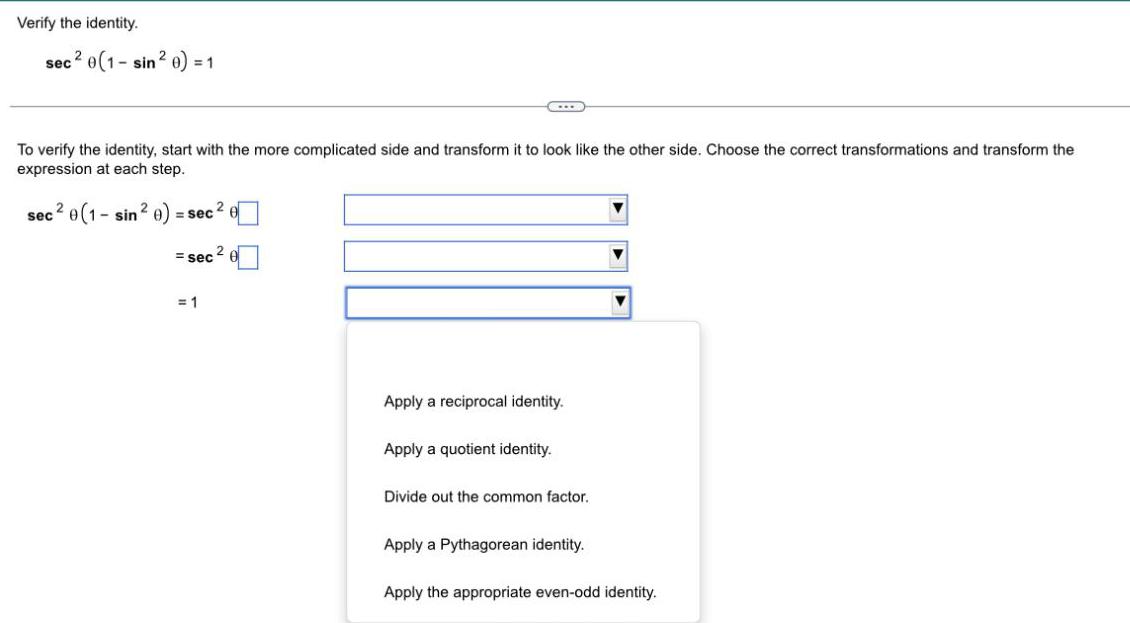
Trigonometric equationsVerify the identity.
sec ² θ(1-sin ² θ) = 1
To verify the identity, start with the more complicated side and transform it to look like the other side. Choose the correct transformations and transform the expression at each step.

Math - Others
Trigonometric equationsThe bearing from A to C is S61° E The bearing from A to B is N 87° E. The bearing from B to C is S 29° W A plane flying at 250 mph takes 3 4 hr to go from A to B.
Find the distance from A to C
The distance from A to C is mi
(Round to the nearest integer as needed.)


Math - Others
Trigonometric equationsThe trend of covid cases in Ontario seems to be a neverending sinusoidal function of ups and downs. If the trend eventually becomes the seasonal flu over a 12-month period, with a minimum number impacted in August of 100 cases. Create an equation of such a cosine function that will ensure the minimum number of cases is 100. Note that the maximum cases can be any reasonable value of your choice. Assume 0 = December, 1 = January, 2 = February and so on.

Math - Others
Trigonometric equationsSimplify sin² (t) + cos² (t) / cos² (t) to an expression involving a single trig function with no fractions.
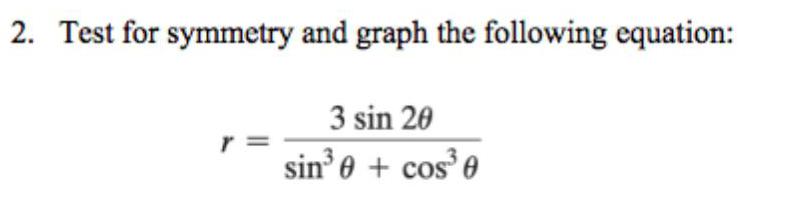
Math - Others
Trigonometric equations2. Test for symmetry and graph the following equation:
r=3 sin 2θ/sin³ θ + cos^3 θ

Math - Others
Trigonometric equations7. For the given function, state the amplitude and the maximum output for the function:
f(t) = 2sin(t)
The amplitude is 4 and the maximum value is y = 2.
The amplitude is 2 and the maximum value is y = 4.
The amplitude is 2 and the maximum value is y = 2.
The amplitude is 4 and the maximum value is y = 4.

Math - Others
Trigonometric equationsGive the exact value of the expression without using a calculator.
cos (tan-¹(-8))