Açısal Momentum Nedir?
Açısal momentum, bir cismin dönme hareketi sırasında taşıdığı dönme miktarını ifade eden bir kavramdır. Açısal momentum, cismin kütlesinin ve dönme hızının çarpımı olarak hesaplanır. Bir cismin açısal momentumu, cismin dönme eksenine göre belirlenir ve vektörel bir niceliktir. Açısal momentum, bir cismin dönme hareketini sürdürme eğilimini gösterir.
Açısal momentum (L) şu formülle ifade edilir:
L = I * ω
Burada:
- L, açısal momentumu temsil eder.
- I, cismin eylemsizlik momentnii (anlık döndürme eksenine göre direncini) ifade eder.
- ω, cismin açısal hızını ifade eder.
Bu formül, bir cismin açısal momentumunun, cismin eylemsizlik momenti ile açısal hızının çarpımı olduğunu gösterir. Eylemsizlik momenti, bir cismin dönme hareketi sırasında üzerine etki eden döndürme direncini temsil eder.
Açısal momentumun korunumu ilkesi, bir sistemdeki net açısal momentumun sabit olduğunu belirtir, bu da bir sistemin dönme hareketinin korunmuş bir nicelik olduğunu gösterir. Bu ilke, dıştan gelen bir net döndürme momenti olmadığı sürece bir sistemdeki açısal momentumun değişmeyeceğini ifade eder.

Açısal Momentum Nasıl Hesaplanır?
Açısal momentum (L) hesaplamak için kullanılan genel formül şu şekildedir:
L = I * ω
Bu formülde:
- L, açısal momentumu temsil eder (bir vektör olarak düşünülebilir).
- I, cismin eylemsizlik momentini (anlık döndürme eksenine göre direncini) ifade eder.
- ω, cismin açısal hızını ifade eder.
Bu formül, bir cismin açısal momentumunu hesaplamak için kullanılır. Ancak, cismin eylemsizlik momenti (I) ve açısal hız (ω) değerlerini bilmek gereklidir.
Eylemsizlik momenti (I), bir cismin kütlesinin ve şeklinin dönme ekseni etrafındaki dağılımına bağlı olarak değişir. Farklı geometriler için eylemsizlik momenti farklı formüllerle hesaplanabilir. Örneğin, bir çubuğun etrafında dönmesi durumunda, çubuğun uzunluğu ve dönme ekseni arasındaki mesafe göz önüne alınarak eylemsizlik momenti hesaplanabilir.
Açısal hız (ω), bir cismin birim zamandaki açısal değişimini ifade eder. Açısal hız, genellikle radyan cinsinden ölçülür. Eğer bir cismin devir hareketi varsa, açısal hız (ω) devir sayısı ile 2π çarpılarak elde edilebilir.
Açısal momentum, bir sistemin dönme hareketini karakterize eden önemli bir fiziksel niceliktir ve eylemsizlik momenti ile açısal hızın çarpımı olarak hesaplanır.
Açısal Momentum Formülü
Bilmemiz gereken üç adet açısal momentum formülü aşağıdaki gibidir:
- L = P.r
- L: açısal momentum
- P: çizgisel momentum
- r: yarıçap
- L = m.V.r
- L = I.ω
- I: eylemsizlik momenti
- ω: açısal hız
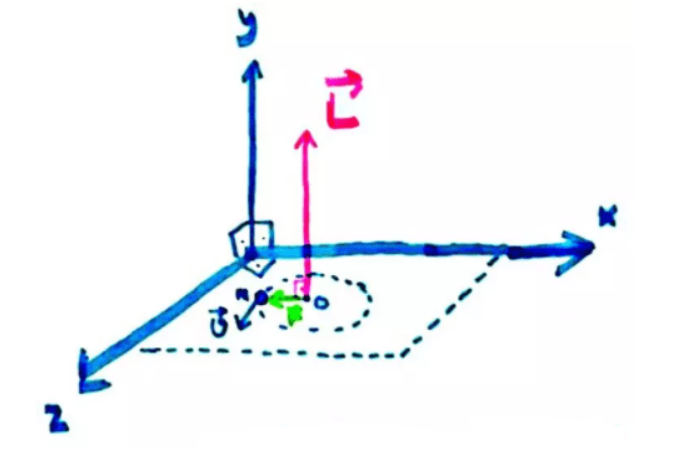
m kütleli noktasal parçacığın, O noktasına göre açısal momentumu, L=ω.I ile hesaplanır.
Açısal Momentumun Korunumu
- Lilk = Lson
- Ii.ωi = Is.ωs
Açısal momentumun korunumu, bir sistemdeki açısal momentumun zaman içinde değişmediği ve sabit kaldığı fiziksel bir prensiptir. Bu prensip, izole bir sistemde dış tork veya dış moment etkileşimi olmaksızın açısal momentumun korunduğunu belirtir.
Açısal momentumun korunumu prensibi, izole bir sistemde dış tork olmadığında, toplam açısal momentumun sabit kalacağını belirtir.
Bu prensip, birçok fiziksel sistemde gözlemlenir. Örneğin, bir topaç döndüğünde ve dış torklar olmadığında, topaç üzerindeki açısal momentum korunur. Aynı şekilde, bir uzay aracı veya bir uçak döndüğünde, eğer dış torklar olmadan izole bir sistemse, açısal momentum korunur.
Açısal Momentum Nasıl Artar?
Açısal momentum (L), bir cismin eylemsizlik momenti (I) ve açısal hız (ω) değerlerinin çarpımı olarak hesaplandığı için, açısal momentumu artırmak için bu iki faktörden biri veya her ikisi de artırılabilir. İşte açısal momentumun artması için bazı faktörler:
- Açısal Hızın Artırılması (ω): Eğer bir cismin dönme hızı artarsa, açısal momentum da artar. Açısal hız, bir cismin birim zamandaki açısal değişimini temsil eder. Bu nedenle, daha hızlı dönen bir cismin açısal momentumu daha yüksek olacaktır.
- Eylemsizlik momentinin Artırılması (I): Cismin meylemsizlik momenti değeri, cismin kütlesinin ve şeklinin dönme ekseni etrafındaki dağılımına bağlıdır. Eylemsizlik momenti arttıkça, açısal momentum da artar. Örneğin, cismin kütlesi daha uzak bir bölgeye dağılmışsa veya şekli değişirse, eylemsizlik momenti büyür ve açısal momentum artar.
- Kuvvet ve Moment Etkileşimleri: Bir cisme dışarıdan uygulanan bir net döndürme momenti (torque), cismin açısal momentumunu değiştirebilir. Bu durumda, açısal momentumun artması veya azalması, dış kuvvetlerin ve momentlerin etkisiyle olabilir.
Açısal momentumun korunumu ilkesine göre, bir sistemin net dış döndürme momenti yoksa, sistemin toplam açısal momentumu korunacaktır. Bu, bir cismin başlangıçtaki açısal momentumunun, döndüğü eksende etkileşim olmazsa değişmeyeceği anlamına gelir.
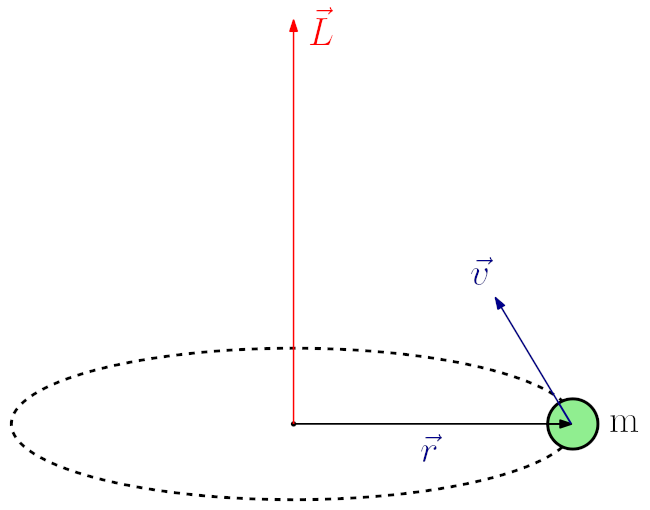
Açısal Momentumun Yönü
Açısal momentumun yönü, ilgili dönme hareketinin doğrultusunu belirtir. Açısal momentum, bir cismin dönme hızı ve dönme eksenine olan uzaklığına bağlı olarak hesaplanan bir vektördür. Açısal momentumun yönü, sağ el kuralı veya sağ el kavramı gibi kural ve kurallar kullanılarak belirlenebilir.
Sağ el kuralı, bir cismin dönme eksenine olan yönlendirmesini belirleme amacıyla kullanılan bir kuraldır. Bu kurala göre, bir cismin dönme ekseni boyunca parmaklarınızı doğrulttuğunuzda, baş parmağınızın gösterdiği yönde açısal momentumun yönü bulunur. Örneğin, bir tekerleği saat yönünde çeviriyorsanız, açısal momentumun yönü tekerleğin dönüş yönüne doğru olacaktır.
Açısal Momentum ve Tork
Açısal momentum, bir cismin dönme hareketi sırasında sahip olduğu devinim miktarını ifade eden bir kavramdır. Açısal momentum, cismin kütlesinin ve dönme hızının çarpımı olarak hesaplanır. Açısal momentumun formülü şu şekildedir:
L = Iω
Burada:
- L, açısal momentumu temsil eder (birim: kg m²/s),
- I, cismin eylemsizlik momenti değerini ifade eder (birim: kg m²),
- ω, cismin açısal hızını temsil eder (birim: rad/s).
Tork ise bir cismin dönme hareketinde etki eden dış kuvvetin neden olduğu açısal hız değişimini ifade eder. Tork, açısal momentumun birim zamandaki değişimini temsil eder. Torkun formülü şu şekildedir:
τ = Iα
Burada:
- τ, torku temsil eder (birim: Nm veya kg m²/s²),
- I, yine eylemsizlik momenti değerini ifade eder (birim: kg m²),
- α, açısal ivmeyi temsil eder (birim: rad/s²).
Açısal momentum ve tork arasındaki ilişki, Newton’ın ikinci yasasının açısal formu olarak da ifade edilebilir:
τ = dL / dt
Bu denklem, torkun, açısal momentumun zamanla değişiminin birinci türevidir.
Genel olarak, bir cismin açısal momentumu, üzerine etki eden tork ile ilişkilidir. Tork, cismin dönme hareketindeki değişiklikleri yönlendirir ve açısal momentumu etkiler. Bu temel prensipler, çeşitli fiziksel sistemlerdeki dönme hareketlerini anlamak için kullanılır.
Dönüş, Orbital ve Toplam Açısal Momentum
Dönme hareketi sırasında, bir cismin açısal momentumu, cismin dönme ekseni etrafındaki dönme hareketinden kaynaklanır. Ancak, bir cismin açısal momentumu sadece kendi etrafında döndüğündeki hareketini değil, aynı zamanda herhangi bir orbital (yörüngesel) hareketini de içerir.
Açısal Momentum (L)
Açısal momentum, bir cismin dönme hareketinden kaynaklanan devinim miktarını ifade eder.
Açısal momentumun formülü L = Iω şeklinde ifade edilir, burada L açısal momentumu, I eylemsizlik momenti ve ω açısal hızdır.
Açısal momentum, cismin kütlesinin ve dönme hızının çarpımına eşittir. Eylemsizlik momenti, cismin kütlesinin ve şeklinin bir fonksiyonu olarak belirlenir.
Orbital Açısal Momentum
Bir cismin orbital hareketi sırasında sahip olduğu açısal momentum, cismin yörüngesel hareketinden kaynaklanır.
Orbital açısal momentum, cismin kütlesinin ve yörüngenin şekline bağlı olarak belirlenen bir eylemsizlik momenti ile orbital hızın çarpımına eşittir.
Formülü genellikle Lorbital = mvr şeklinde ifade edilir, burada m kütle, v hız ve r yarıçapı temsil eder.
Toplam Açısal Momentum
Toplam açısal momentum, hem dönme hareketinden hem de orbital hareketten kaynaklanan açısal momentumun toplamıdır.
Toplam açısal momentum (Ltoplam), dönme hareketinden gelen (L) ve orbital hareketten gelen (Lorbital) açısal momentumların toplamına eşittir: Ltoplam = L + Lorbital.
Açısal Momentum ile Eylemsizlik Momenti Arasındaki İlişki
Açısal momentum (angular momentum) ile eylemsizlik momenti (moment of inertia veya atılma momenti) arasında bir ilişki vardır ve bu iki terim birbirine bağlıdır. İkisi de bir cismin dönme hareketi ile ilgili fiziksel büyüklüklerdir.
Açısal momentum (L), bir cismin dönme hareketinden kaynaklanan devinim miktarını ifade eder ve şu formülle ifade edilir
L = Iω
Açısal momentum (angular momentum) ile eylemsizlik momenti (moment of inertia veya atılma momenti) arasında bir ilişki vardır ve bu iki terim birbirine bağlıdır. İkisi de bir cismin dönme hareketi ile ilgili fiziksel büyüklüklerdir.
Açısal momentum (L), bir cismin dönme hareketinden kaynaklanan devinim miktarını ifade eder ve şu formülle ifade edilir:
L = Iω
Burada:
- L, açısal momentumu temsil eder,
- I, eylemsizlik momentini (atılma momenti) temsil eder,
- ω, cismin açısal hızını temsil eder.
Bu formül, bir cismin açısal momentumunun, cismin eylemsizlik momenti ile açısal hızının çarpımına eşit olduğunu gösterir. Eylemsizlik momenti, bir cismin dönme hareketindeki direnci veya “ağırlığını” belirleyen bir ölçüdür. Farklı şekil, yoğunluk dağılımı ve dönme ekseni konumlarına göre eylemsizlik momenti değişebilir.
Bu formüldeki ilişki, cismin dönme hareketinin hızının ve şeklinin açısal momentum üzerindeki etkisini gösterir. Eğer eylemsizlik momenti büyükse ve açısal hız sabit kalırsa, açısal momentum artar. Eğer eylemsizlik momenti küçükse, açısal hızın artması açısal momentumun büyümesine neden olabilir.
Açısal momentumun korunumu prensibi, bir sistemde dış tork olmadığında açısal momentumun sabit kalacağını belirtir. Bu prensip, eylemsizlik momenti ile açısal hızın birbirine bağlı olduğunu ve birindeki değişikliğin diğerini etkileyebileceğini gösterir.
Açısal İvme Nedir?
Açısal ivme, bir cismin dönme hareketi sırasında açısal hızındaki değişimi ifade eden bir fiziksel büyüklüktür. Açısal ivme, bir cismin dönme hareketindeki hız değişikliklerini nicel olarak tanımlar. Açısal ivme genellikle α (alfa) harfi ile temsil edilir ve birimi radian cinsinden zamana göre olan değişimdir.
Açısal ivmenin matematiksel tanımı şu şekildedir:
α = dω / dt
Burada:
- α, açısal ivmeyi temsil eder (birimi: rad/s²),
- ω, cismin açısal hızını temsil eder (birimi: rad/s),
- t, zamanı temsil eder.
Açısal ivme, açısal hızın zamana göre türevidir ve genellikle bir cismin dönme hareketindeki değişiklikleri ölçmek için kullanılır. Açısal ivme, bir cismin dönme hareketindeki hız değişimini ifade eder. Eğer açısal ivme pozitifse, açısal hız artar; eğer negatifse, açısal hız azalır.
Açısal ivme, Newton’un ikinci yasasının açısal formuyla da ilişkilidir:
τ = Iα
Burada:
- τ, torku temsil eder (birimi: Nm veya kg m²/s²),
- I, cismin eylemsizlik momenti değerini temsil eder (birimi: kg m²),
- α, açısal ivmeyi temsil eder (birimi: rad/s²).
Bu denklem, torkun, açısal ivmenin eylemsizlik momenti ile çarpımına eşit olduğunu gösterir. Açısal ivme, dönen bir cismin üzerine etki eden tork ile ilişkilidir ve cismin dönme hareketindeki hız değişikliklerini açıklar.
Kepler Yasası
Johannes Kepler’in gezegenlerin hareketleriyle ilgili olarak formüle ettiği üç temel yasa, Kepler Yasaları olarak bilinir. Bu yasalar, 17. yüzyılın başlarında, özellikle 1609-1619 yılları arasında Kepler tarafından yayımlanan “Astronomia Nova” ve “Harmonices Mundi” adlı eserlerinde açıklanmıştır. Kepler Yasaları, Tycho Brahe’nin gözlemleri üzerine dayanmaktadır.
Birinci Kepler Yasası (Dönme Yasası)
“Bir gezegen, Güneş çevresindeki eliptik bir yörüngede döner. Güneş, elipsin bir odak noktasında bulunur.” Bu yasa, bir gezegenin Güneş çevresindeki yörüngesinin eliptik (oval) bir şekilde olduğunu ifade eder. Yani, bir gezegen Güneş’e eşit uzaklıkta dönmez, bu uzaklık eliptik yörüngede değişir. Güneş, elipsin bir odak noktasında bulunur, ancak elipsin merkezinde değil.
İkinci Kepler Yasası (Eşit Alanlar Yasası)
“Bir gezegen, Güneş’e olan çekim kuvveti nedeniyle eşit zaman aralıklarında eşit alanlar tarar.” Bu yasa, bir gezegenin Güneş etrafındaki yörüngesinde eşit zaman aralıklarında eşit alanları taradığını belirtir. Yani, bir gezegen Güneş’e daha yaklaştığında daha hızlı hareket eder ve bu durum, birim zamanda taradığı alanın büyümesine neden olur.
Üçüncü Kepler Yasası (Periyot-Çap İlişkisi)
“Bir gezegenin yörüngesinin yarı büyük ekseni ile küpü, gezegenin yörüngesini tamamlama süresinin karesi orantılıdır.” Bu yasa, bir gezegenin Güneş etrafındaki yörüngesinin periyodu ile yarı büyük ekseni arasında bir matematiksel ilişki kurar. Yarı büyük eksen, bir eliptik yörüngenin yarı uzunluğunu temsil eder.
Topaç ve Jiroskop
Topaç ve jiroskop, fizikte dönme hareketleri ve açısal momentum konularında önemli olan iki cihazdır. Her ikisi de açısal momentumun korunumu prensipleri üzerine çalışır.Bir topaç, genellikle bir sapın üzerinde dönen bir küreden veya diskten oluşan basit bir oyuncaktır.
Topaç, açısal momentumun korunumu ilkesini gösteren güzel bir örnektir. Bir topaç dönmeye başladığında, üzerinde bir açısal momentum oluşur. Topaç bir nokta etrafında döndüğü için, açısal momentum korunur. Eğer dış bir kuvvet etkilemezse, topaç kendiliğinden bir süre boyunca dönmeye devam eder.Bir jiroskop, genellikle hızla dönen bir diskten oluşan bir cihazdır ve bu disk genellikle bir çerçeve içinde monte edilmiştir.
Bir jiroskop, dönme hareketinin korunumu ilkesini kullanarak özellikle açısal değişimlere karşı direnç gösterir. Jiroskoplar, uçaklar, gemiler ve uzay araçları gibi çeşitli makinelerde kullanılır. Örneğin, uçakların yönünü korumak ve sabit tutmak için jiroskoplar kullanılır. Bu, açısal momentumun korunumu prensibine dayanır.
Her iki cihaz da açısal momentumun korunumu ilkesini vurgular ve bu prensipleri kullanarak dönme hareketlerini anlamamıza yardımcı olur. Açısal momentum, bir sistemin dönme hareketinin miktarını ve yönetimini belirleyen önemli bir fiziksel büyüklüktür.

Öteleme Hareketi vs. Dönme Hareketi
| Özellik | Öteleme | Dönme |
|---|---|---|
| Harekete karşı gösterilen direnç | kütle (m) | eylemsizlik momenti (I) |
| Momentum | çizgisel momentum (P) | açısal momentum (L) |
| Hız | çizgisel hız (v) | açısal hız (w) |
| İvme | çizgisel ivme (a) | açısal ivme (α) |
| İvmenin sebebi (hareket durumunu değiştiren etki) | kuvvet (F) | tork (T) |
| Temel ivme denklemi | F = ma | T = Iα |
| Kinetik enerji | (1/2)mv2 | (1/2)Iw2 |

