Limit ve Süreklilik, AYT Matematik‘teki önemli konulardan biri. Kendisinden sonra gelen Türev, İntegral gibi konular için önemli bilgiler içeriyor. Temel kuralları ve yöntemleri öğrendikten sonra bolca pratik yapman gerekiyor. Soru çözmeye başladıktan sonra bu konunun sana çok kolay geleceğine eminiz! Konu anlatımının sonundaki Limit sorularına bakmayı unutma! Kunduz ekibinden Nurseli, bu konu hakkında senin için çok faydalı bir yazı hazırladı!
İpuçlarıyla Limit Konu Anlatımı
LİMİT VE SÜREKLİLİK
LİMİTTE SÜREKLİLİK TANIMI
Limit ve Süreklilik Konu Anlatımı
Limit Nedir? Limitin Tanımı Nedir? Limit Ne Demek? Limit Nasıl Alınır?
Bir f(x) fonksiyonunda x değişkenine bir a değerine sınırsız yaklaşan değerler verildiğinde fonksiyondaki f(x) değerleri de bir L değerine sınırsız yaklaşıyorsa; bu L değerine f(x) fonksiyonunun a değeri için limiti denir. Limit şu şekilde gösterilir:
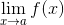
Bu tanımı daha da anlaşılır kılmak için örnek verelim:

Sağdan ve Soldan Limit – Sağ Limit ve Sol Limit
Bir f(x) fonksiyonunda x’e, bir a değerine sınırsız yaklaşan değerler x < a koşulu ile verildiğinde f(x) değerleri de bir L1 değerine sınırsız yaklaşıyorsa; bu L1 değerine f(x) fonksiyonunun a değeri için soldan limiti; x > a koşulu ile verildiğinde f(x) değerleri de bir L2 değerine sınırsız yaklaşıyorsa; bu L2 değerine f(x) fonksiyonunun a değeri için sağdan limiti denir.
Süreklilik Nedir? Süreklilik Ne Demek? Fonksiyonların Sürekliliği
x = a değerinde f fonksiyonun sürekli olması için,

Bu üç koşuldan birinin sağlanmadığı durumda f fonksiyonu x = a değeri için süreksiz olur.
“Fonksiyonun sürekliliği ancak tanım kümesindeki noktalarda araştırılır. Tanımsız olduğu noktalarda sürekliliği tartışmak anlamsızdır.”
Limit ile İlgili Doğru Bilinen Yanlışlar – Limit Konusu Karıştırılan Kavramlar
- Bir fonksiyonun limit değeri o fonksiyonun asla ulaşamadığı bir değerdir.
YANLIŞ. Bir fonksiyon belirli bir a reel sayısında bir görüntüye sahip olabilir. Bu da fonksiyon x’den a’ya giderken o noktaya ulaşabildiğini söyler.
- Limit, bir x değeri belli bir noktaya yaklaşırken, bir fonksiyonun değerinin nasıl değiştiğini açıklar.
YANLIŞ. Çünkü, limit kavramı fonksiyonun o noktada ne yaptığını değil o noktanın civarında ne yaptığını inceler. Bir fonksiyonun belirli bir a reel sayısında bir görüntüye sahip olması ya da olmaması fonksiyonun o noktadaki limitini etkilemez.
- Bir fonksiyonun bir noktada birden çok limit değeri olabilir.
YANLIŞ. Bir fonksiyonun bir noktada sadece bir limit değeri vardır.
- Bir fonksiyonun sürekli olmadığı noktalarda limiti yoktur.
YANLIŞ. Bilindiği gibi, bir fonksiyonun bir noktadaki limitinin varlığı, fonksiyonun söz konusu noktada tanımlı ve sürekli olmasına bağlı değildir. Dolayısıyla limit için süreklilik ve tanımlılık ön koşul olmamaktadır.
- Bir fonksiyonun bir noktada sürekli olması için o noktada limitinin olması gerekir.
DOĞRU. Yukarıda da bahsettiğimiz üzere fonksiyonların sürekliliği başlığında 3 koşulumuz vardı.
- Sürekli bir fonksiyonun grafiğinde hiçbir kopukluk, kesiklik ya da kırıklık yoktur.
YANLIŞ. Sürekli bir fonksiyonun grafiğinde kopukluk, kesiklik ya da kırıklıklar OLABİLİR. Aşağıdaki örneğe bakalım, fonksiyonda kırıklık var ama sürekli bir fonksiyon.

Limit Kuralları ve Limit Formülleri

Limit ve Süreklilik Soru Çözümü – Limit Soru Çözümü
12. Sınıf Limit konu anlatımı yazımızın sonuna geldik! Konuyu tam olarak anlamak için bol bol soru çözümü yapmak da çok önemli. Kunduz’a şu ana kadar sorulmuş binlerce Limit ve Süreklilik konulu soruyu aşağıdan inceleyebilirsin.
Referanslar:
Baştürk, Savaş, and Gülden Dönmez. “Mathematics student teachers’ misconceptions on the limit and continuity concepts.” Necatibey Faculty of Education Electronic Journal of Science and Mathematics Education 5.1 (2011): 225-249.
☀️☀️☀️
Sınava hazırlık uzun bir maraton. Kunduz ekibi olarak bu yolculukta yanında olmayı çok isteriz! Alanında uzman Profesyonel eğitmenler tarafından hazırlanan Soru Çözümü, binlerce soru ve çözümden oluşan Soru Bankası hizmetlerimizden faydalanabilirsin.



