The derivative of arctan(x), also known as the tangent inverse, is an essential concept in calculus. It allows us to find the rate of change of the arctan function with respect to its input variable. Understanding the derivative of arctan(x) is crucial in various fields such as physics, engineering, and mathematics.
In this article, we will explore the derivative of arctan(x) in detail. We will discuss its definition, formulas, proofs, and practical applications. By the end of this article, you will have a solid understanding of how to differentiate the arctan function and apply it to solve real-world problems.
So, let’s dive into the fascinating world of the derivative of arctan(x)!
What is Arctangent?
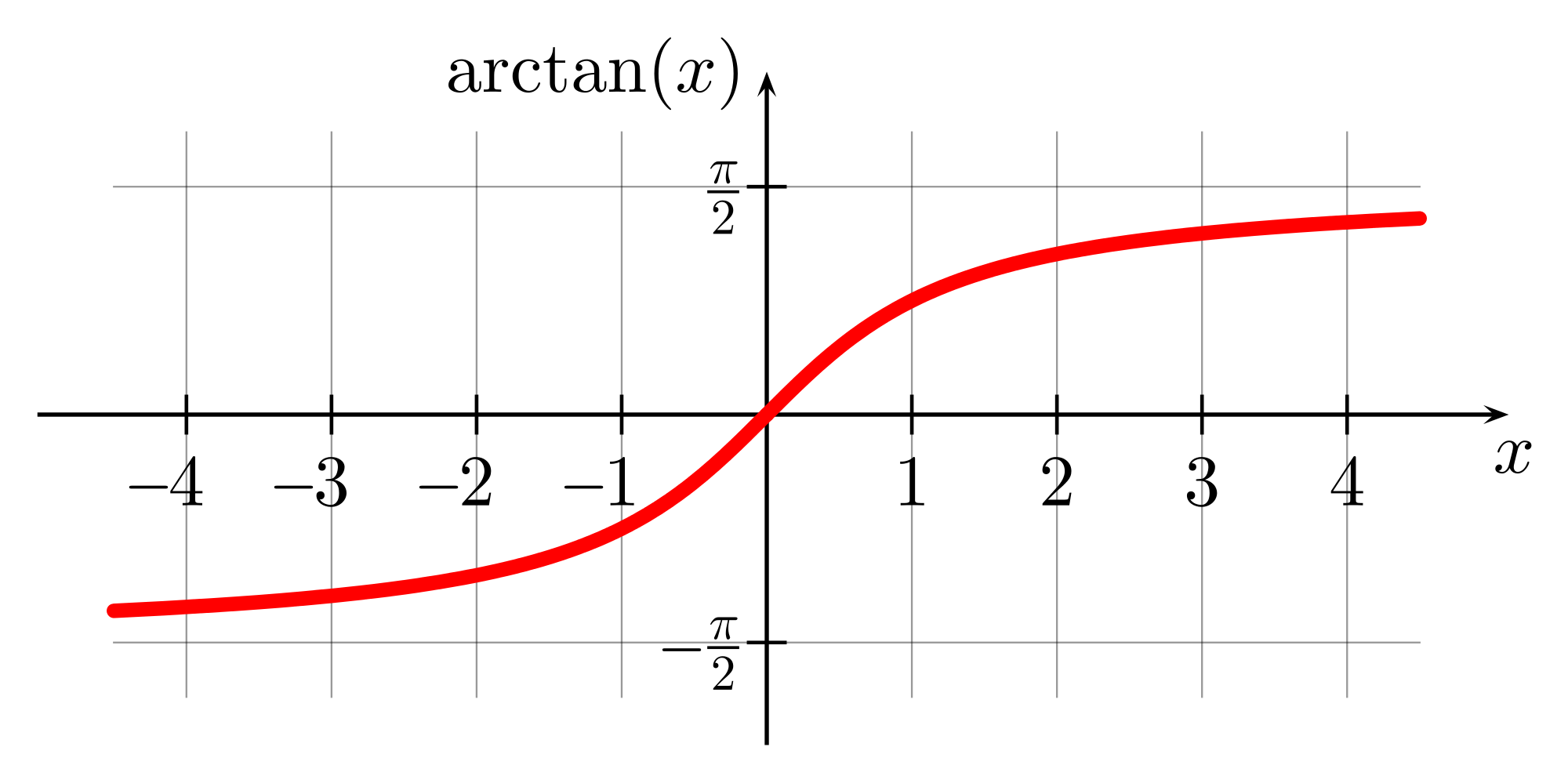
Before we delve into the derivative of arctan(x), let’s first understand what the arctan function is. Arctan, denoted as tan⁻¹(x) or atan(x), is the inverse function of the tangent function. In other words, if y = arctan(x), then tan(y) = x.
The arctan function maps real numbers to angles, specifically the angle whose tangent is equal to the given input value. It is defined for all real values of x, ranging from negative infinity to positive infinity. The output of the arctan function lies between -π/2 and π/2, representing the principal values of the inverse tangent.
.png)
What is the Derivative of Arctan(x)?
The derivative of arctan(x), denoted as d/dx(arctan(x)) or (arctan(x))’, represents the rate of change of the arctan function with respect to its input variable x. It measures how the output of the arctan function varies as x changes.
The derivative of arctan(x) can be expressed using different mathematical representations. The most commonly used formula is:
d/dx(arctan(x)) = 1 / (1 + x²)
This formula tells us that the derivative of arctan(x) is equal to 1 divided by the sum of 1 and the square of x. It is important to note that this derivative formula holds true for all real values of x.
If you want to learn other trigonometric functions’ derivatives, you can read our content about: Differentiation of Trigonometric Functions
Derivative of Arctan(x) Formula
The derivative formula for arctan(x) is derived using various methods such as the chain rule, quotient rule, or first principles. In this section, we will explore two popular methods for proving the derivative of arctan(x): the first principles and the chain rule.
Derivative of Arctan(x) Proof by First Principles
The first principles approach involves using the fundamental definition of the derivative to derive the derivative formula for arctan(x). Let’s go through the step-by-step process:
Step 1: Assume f(x) = arctan(x).
Step 2: Calculate the difference quotient using the definition of the derivative:
[f(x + h) – f(x)] / h
Step 3: Substitute the arctan function into the difference quotient:
[arctan(x + h) – arctan(x)] / h
Step 4: Simplify the expression using trigonometric identities and algebraic manipulation.
Step 5: Take the limit as h approaches 0 to find the derivative formula.
Derivative of Arctan(x) Proof by Chain Rule
The chain rule is another method commonly used to prove the derivative of arctan(x). The chain rule states that if y = f(g(x)), then the derivative of y with respect to x is given by dy/dx = f'(g(x)) * g'(x).
To prove the derivative of arctan(x) using the chain rule, we start by assuming y = arctan(x) and rewrite it as x = tan(y). Then, we differentiate both sides of the equation with respect to x:
d/dx(x) = d/dx(tan(y))
Simplifying the equation and applying trigonometric identities, we can derive the derivative formula for arctan(x).
Graph of Derivative of Arctan(x)
To gain a visual understanding of the derivative of arctan(x), let’s examine its graph. The graph of the derivative represents how the slope of the arctan function changes at different points.
Insert Graph Image Here
As shown in the graph, the derivative of arctan(x) is always positive for all values of x. It starts from zero at x = 0 and approaches zero as x tends to positive or negative infinity. The graph is symmetric about the y-axis, indicating that the derivative of arctan(x) is an odd function.
Anti-Derivative of Arctan(x)
The anti-derivative, also known as the indefinite integral, of arctan(x) can be found by reversing the process of differentiation. The anti-derivative of arctan(x) is denoted as ∫arctan(x)dx.
To find the anti-derivative of arctan(x), we can use integration techniques such as substitution or integration by parts. The result will be a function whose derivative is equal to arctan(x) plus a constant of integration.
Derivative of Negative Arctan(x)
The derivative of the negative arctan function, -arctan(x), is equal to the negative of the derivative of arctan(x). In other words, d/dx(-arctan(x)) = -[d/dx(arctan(x))].
This property holds true because differentiation is a linear operation, meaning it preserves scalar multiplication.
Derivative of Inverse Arctan(x)
The derivative of the inverse arctan function, arctan⁻¹(x), is equal to the derivative of arctan(x) with respect to x. In mathematical notation, d/dx(arctan⁻¹(x)) = d/dx(arctan(x)).
This property arises from the fact that the inverse function of a function has the same derivative as the original function.
Derivative of Arctan Example Problems
Now that we understand the concept and formula of the derivative of arctan(x), let’s apply it to solve some example problems. These problems will help solidify our understanding and demonstrate how the derivative of arctan(x) can be used in real-world scenarios.
Derivative of Arctan(2x)
To find the derivative of arctan(2x) with respect to x, we can use the derivative formula for arctan(x) and apply the chain rule.
Step 1: Let’s set u = 2x.
Step 2: Calculate the derivative of u with respect to x: u’ = 2.
Step 3: Apply the derivative formula for arctan(x) and the chain rule:
d/dx(arctan(2x)) = (1 / (1 + (2x)²)) * 2
Step 4: Simplify the expression to obtain the final result:
d/dx(arctan(2x)) = 2 / (1 + 4x²)
Therefore, the derivative of arctan(2x) with respect to x is 2 / (1 + 4x²).
Derivative of Arctan(1/x)
To find the derivative of arctan(1/x) with respect to x, we can again use the derivative formula for arctan(x) and apply the chain rule.
Step 1: Let’s set u = 1/x.
Step 2: Calculate the derivative of u with respect to x: u’ = -1/x².
Step 3: Apply the derivative formula for arctan(x) and the chain rule:
d/dx(arctan(1/x)) = (1 / (1 + (1/x)²)) * (-1/x²)
Step 4: Simplify the expression to obtain the final result:
d/dx(arctan(1/x)) = -1 / (x²+ 1)
Therefore, the derivative of arctan(1/x) with respect to x is -1 / (x² + 1).
Derivative of Arctan(4x)
To find the derivative of arctan(4x) with respect to x, we can once again use the derivative formula for arctan(x) and apply the chain rule.
Step 1: Let’s set u = 4x.
Step 2: Calculate the derivative of u with respect to x: u’ = 4.
Step 3: Apply the derivative formula for arctan(x) and the chain rule:
d/dx(arctan(4x)) = (1 / (1 + (4x)²)) * 4
Step 4: Simplify the expression to obtain the final result:
d/dx(arctan(4x)) = 4 / (1 + 16x²)
Therefore, the derivative of arctan(4x) with respect to x is 4 / (1 + 16x²).
Derivative of Arctan(x² + 1)
To find the derivative of arctan(x² + 1) with respect to x, we can once again use the derivative formula for arctan(x) and apply the chain rule.
Step 1: Let’s set u = x² + 1.
Step 2: Calculate the derivative of u with respect to x: u’ = 2x.
Step 3: Apply the derivative formula for arctan(x) and the chain rule:
d/dx(arctan(x² + 1)) = (1 / (1 + (x² + 1)²)) * 2x
Step 4: Simplify the expression to obtain the final result:
d/dx(arctan(x² + 1)) = 2x / (x^4 + 2x² + 2)
Therefore, the derivative of arctan(x² + 1) with respect to x is 2x / (x^4 + 2x² + 2).
These example problems demonstrate how to apply the derivative formula for arctan(x) to specific functions and find their derivatives. It is essential to practice solving such problems to develop a deeper understanding of the concept.
Common Misconceptions Related to Derivative of Arctan(x)
While studying the derivative of arctan(x), there are a few common misconceptions that students often encounter. Let’s address these misconceptions and clarify the correct understanding of the derivative of arctan(x).
Misconception 1: Arctan is the derivative of tan.
Contrary to popular belief, arctan is not the derivative of the tangent function. The derivative of the tangent function is sec²(x). However, the derivative of the arctan function is 1 / (1 + x²).
Misconception 2: The derivative of arctan(x) is always positive.
While it is true that the derivative of arctan(x) is positive for all real values of x, it does not mean that the arctan function is always increasing. The arctan function has a range of -π/2 to π/2, and its rate of change varies depending on the input values.
Misconception 3: Arctan is not differentiable.
Arctan is indeed a differentiable function. Its derivative exists for all real values of x, allowing us to find the rate of change of the arctan function at any point in its domain. The graph of the arctan function is smooth and continuous, indicating its differentiability.
It is crucial to understand and dispel these misconceptions to have a clear and accurate understanding of the derivative of arctan(x).
Derivative of Arctan(x) from Limit Definition
Another approach to finding the derivative of arctan(x) is to use the limit definition of the derivative. This method involves taking the limit of the difference quotient as it approaches zero.
By applying the limit definition, we can prove that the derivative of arctan(x) is indeed 1 / (1 + x²).
How Do You Differentiate Arctangent?
To differentiate the arctangent function, you can use the derivative formula for arctan(x) or the limit definition of the derivative. Both methods will yield the same result: 1 / (1 + x²).
The derivative formula allows for a more straightforward and efficient calculation, especially when dealing with complex expressions involving arctan. However, the limit definition of the derivative provides a more rigorous and fundamental approach to understanding the derivative conceptually.
Is Arctan(x) Differentiable?
Yes, the arctan function is differentiable for all real values of x. Its derivative, which represents the rate of change of the arctan function, exists at every point in its domain. The differentiability of the arctan function can be observed through its smooth and continuous graph.
Solved Examples of Derivative of Arctan(x)
Let’s solve a few more examples to solidify our understanding of the derivative of arctan(x).
Example 1: Find the derivative of arctan(3x).
To find the derivative of arctan(3x), we can apply the chain rule.
Step 1: Let’s set u = 3x.
Step 2: Calculate the derivative of u with respect to x: u’ = 3.
Step 3: Apply the derivative formula for arctan(x) and the chain rule:
d/dx(arctan(3x)) = (1 / (1 + (3x)²)) * 3
Step 4: Simplify the expression to obtain the final result:
d/dx(arctan(3x)) = 3 / (1 + 9x²)
Therefore, the derivative of arctan(3x) with respect to x is 3 / (1 + 9x²).
Example 2: Find the derivative of arctan(e^x).
To find the derivative of arctan(e^x), we can again apply the chain rule.
Step 1: Let’s set u = e^x.
Step 2: Calculate the derivative of u with respect to x: u’ = e^x.
Step 3: Apply the derivative formula for arctan(x) and the chain rule:
d/dx(arctan(e^x)) = (1 / (1 + (e^x)²)) * e^x
Step 4: Simplify the expression to obtain the final result:
d/dx(arctan(e^x)) = e^x / (1 + e^(2x))
Therefore, the derivative of arctan(e^x) with respect to x is e^x / (1 + e^(2x)).
These solved examples demonstrate how to apply the derivative formula for arctan(x) to specific functions and find their derivatives. Practicing these problems will enhance your proficiency in differentiating the arctan function.
How Kunduz Can Help You Learn Derivatives of Arctan(x)
Mastering the derivatives of arctan(x) and other calculus concepts requires practice and guidance. Kunduz is your trusted companion in your journey towards mathematical excellence.
With Kunduz, you can access a comprehensive range of educational resources, including interactive lessons, video tutorials, and detailed explanations. Our platform is designed to provide you with a personalized and immersive learning experience, allowing you to grasp complex mathematical concepts with ease.
Whether you are a student preparing for exams or a professional seeking to enhance your mathematical skills, Kunduz has got you covered. Join our community today and embark on an exciting adventure of mathematical discovery.
In conclusion, the derivative of arctan(x) plays a crucial role in calculus and various scientific disciplines. Understanding its formula, proofs, and applications is essential for solving mathematical problems and gaining insights into the behavior of functions. By following the methods and examples outlined in this article, you can confidently differentiate the arctan function and apply it to solve real-world challenges. So, embrace the world of derivatives and unlock the power of arctan(x) in your mathematical journey!
