Fonksiyon Nedir?
Matematikte değişkenleri girdi olarak kabul eden ve her bir girdiden yalnızca bir çıktı oluşmasını sağlayan kurala fonksiyon denir.
Fonksiyon matematiğin temel konularından biridir. Bunun yanında günlük hayatımızda da fonksiyon kavramını fark etmeden sıkça kullanmaktayız. Örneğin bir manava gittiğinizde aldığınız ürünün miktarına göre ödenecek tutar da değişir. Ürün miktarı ve ödenecek tutar arasındaki ilişkiyi bir örnekle inceleyelim. Bir kilo elmanın 10 TL olduğunu varsayarsak bir kilo elma alan kişi 10 tl öderken, 3 kilo elma alan biri ise 30 TL ödeme yapar. Bu örnekte alınan elma miktarı girdi iken, ödenecek tutar ise çıktıdır.
- Örneğimizi incelediğimiz de her bir girdi için bir çıktı hesaplayabiliyoruz.
- Alınan elma miktarına göre ödenecek ücret yani çıktımız ise yalnızca bir tanedir.
Fonksiyon kavramının matematiksel tanımına geçmeden önce, fonksiyonların iki çokluk arasında bu iki şartı sağlayabilen bağıntılar olduğunu söyleyebiliriz.
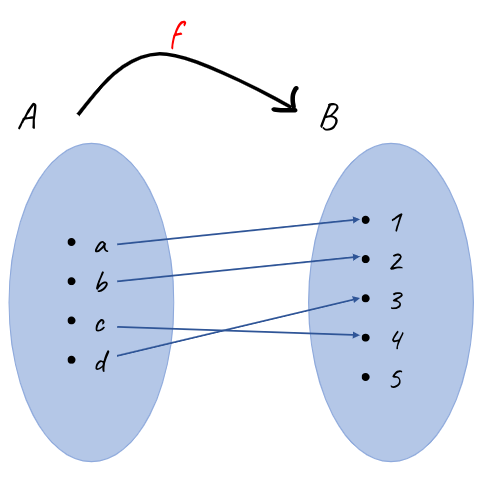
A ve B boş olmayan iki küme olsun. A’nın her elamanı B’nin yalnız bir elemanına eşleyen f bağıntısına A’dan B’ye tanımlı bir fonksiyon denir.
f : A → B biçiminde gösterilir.
Fonksiyonların Özellikleri
f : A → B şeklinde tanımlı bir fonksiyon,
Birebir ise, A kümesinde tanımlı olduğu her değeri B kümesinden ayrı bir ögeye eşler. Matematiksel olarak; her x1, x2 €A için f(x1)=f(x2) => x1=x2
İçine ise B kümesinde, eşlenmemiş en az bir değer vardır.
Örten ise A kümesindeki bütün ögeler için tanımlıdır.
Matematiksel olarak; her y € B için en az bir x€A vardır öyle ki; f(x)=y’dir.
Tanım Kümesi ve Değer Kümesi
f : A → B biçiminde verilen bir fonksiyon için A tanım kümesi iken, B kümesi fonksiyonun değer kümesidir.
Fonksiyon Türleri
- Bire Bir Fonksiyon
- Örten Fonksiyon
- İçine Fonksiyon
- Sabit Fonksiyon
- Birim Fonksiyon
- Çift ve Tek Fonksiyon
- Ters Fonksiyon
- Bileşke Fonksiyon
- Parçalı Fonksiyon
- Doğrusal (Lineer) Fonksiyon
Bire Bir Fonksiyon
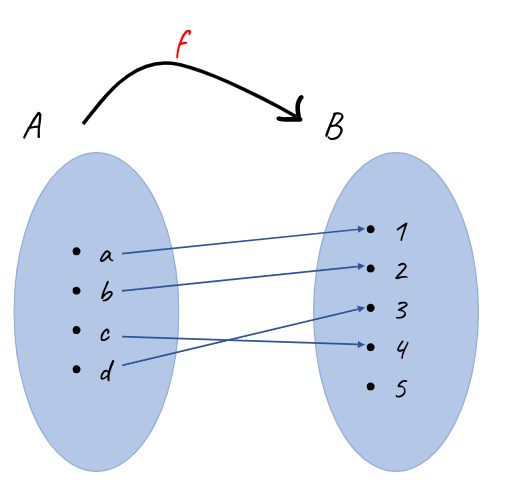
Bir fonksiyonda tanım kümesindeki elemanların görüntüleri de birbirinden farklıysa buna bire bir fonksiyon deriz.
Kural olarak göstermemiz gerekirse: ∀ a,b ∈ A için, f(a) = f(b) iken, a = b oluyorsa f fonksiyonu bire birdir.
Örten Fonksiyon
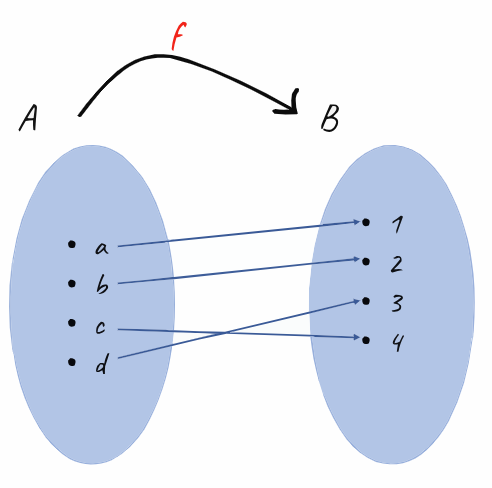
Görüntü kümesiyle değer kümesinin aynı olduğu fonksiyonlara örten fonksiyon deniyor, yani f : A → B biçiminde tanımlanmış fonksiyonumuzda B kümesinin eşi olmayan eleman olmaması gerekiyor!
İçine Fonksiyon
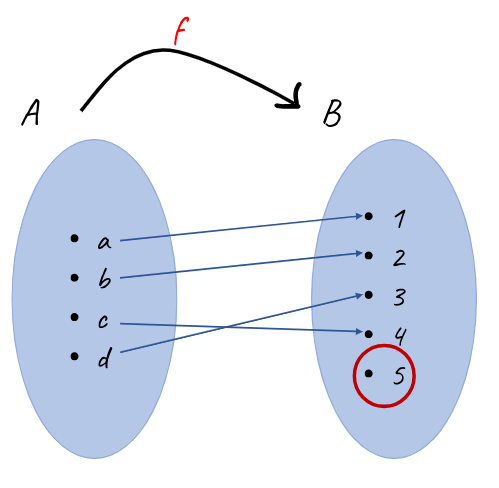
f : A → B biçiminde tanımlanmış fonksiyonumuzda değer kümesinde, yani B kümesinde, eşi olmayan eleman varsa bunu içine fonksiyon deriz.
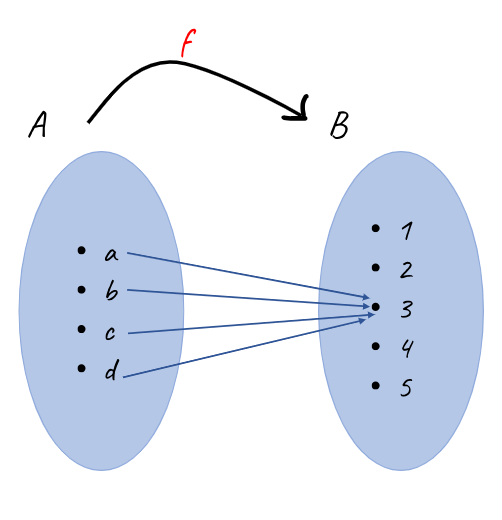
Sabit Fonksiyon
Birim fonksiyonla birlikte hatırlaması en kolay olan fonksiyon sabit fonksiyondur. Sabit fonksiyonda A kümesindeki her bir eleman B kümesindeki tek bir elemana eştir. Sabit fonksiyon:
∀x ∈ A ve c ∈ B için, f : A → B f(x) = c şeklinde tanımlanır. Buradaki “c” değeri sabit değeri ifade eder.
Birim Fonksiyon
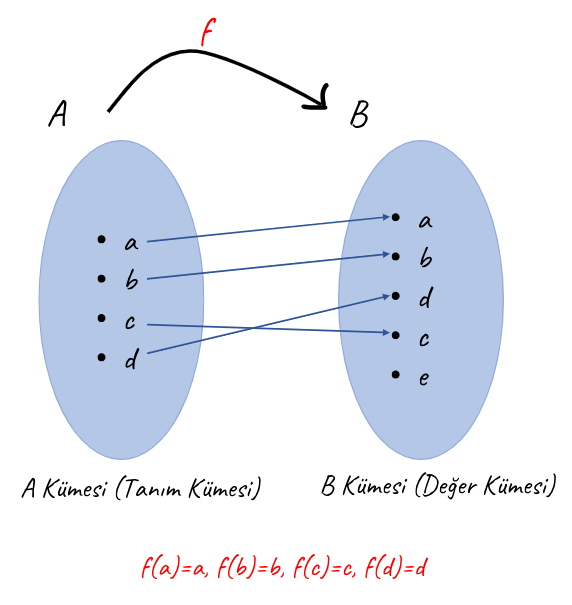
Tanım kümesindeki her eleman B kümesinde kendisiyle eşlenirse buna birim fonksiyon deriz. Birim fonksiyon “ I “ ile gösterilir.
Çift ve Tek Fonksiyon
Çift fonksiyonlar f(x) = f(-x) fonksiyonlardır. Mesela f(2)’nin f(-2)’ye eşit olması gibi.
Eğer f(x) = -f(x) ise bu durumda da tek fonksiyon deriz. Mesela f(2)’nin f(2)’ye eşit olması gibi.
Çift fonksiyonlar y eksenine göre simetrik iken, tek fonksiyonlar orijine göre simetriktir.
Ters Fonksiyon
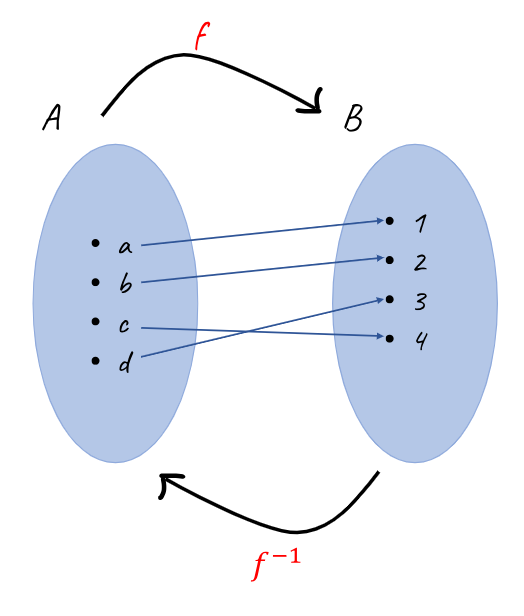
Elimizde yukarıda bahsettiğimiz gibi birebir ve örten bir fonksiyon olması gerekiyor: şayet öyle bir fonksiyonumuz var ve f: A → B’ye tanımlanmışsa:
Tanım kümesini B, değer kümesini A olarak ters çevirerek ters fonksiyon elde edebiliriz. Böylelikle fonksiyonun tersini alma işlemi uygulanmış olur.
Bileşke Fonksiyon
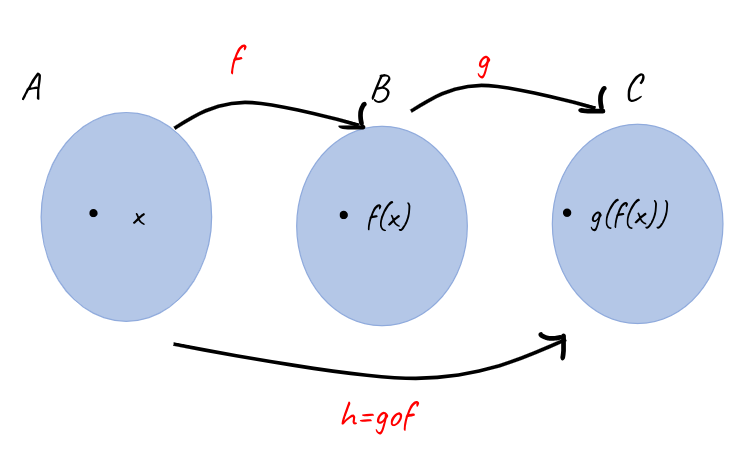
İki veya daha fazla fonksiyonu birleştirerek tek fonksiyon yapmaya bileşke fonksiyon denir.
f : A → B ****ve g : B → C tanımlı fonksiyonlar verilsin.
Bu iki f ve g fonksiyonlarının bileşkesi gof : A → C üzere
gof(x) = g(f(x)) şeklinde gösterilen fonksiyonlara, f ve g fonksiyonlarını bileşkesi denir.
Parçalı Fonksiyon
Parçalı fonksiyon, matematikte tanım aralığı alt aralıklara parçalanan ve her bir alt aralık için farklı bir fonksiyon olarak tanımlanan bir fonksiyon türüdür.
Doğrusal (Lineer) Fonksiyon
a, b reel sayı olmak üzere, f : R → R, f(x) = ax + b şeklindeki fonksiyonlara doğrusal fonksiyon denir.
Fonksiyon Olma Koşulları
Bir bağıntının fonksiyon olabilmesi için:
1)Tanım kümesinde açıkta eleman kalmamalıdır (Değer kümesinde açıkta eleman olabilir).
2)Tanım kümesindeki her elemanın görüntüsü yalnız bir tane olmalıdır.
Fonksiyonlarla İşlemler
- Fonksiyonlarla Toplama İşlemi
- Fonksiyonlarla Çıkarma İşlemi
- Fonksiyonlarla Çarpma İşlemi
- Fonksiyonlarla Bölme İşlemi
Fonksiyonlarla Toplama İşlemi
f : A → R ve g : B → R olmak üzere, f ve g fonksiyonlarının birlikte tanımlı olduğu x değerleri için;
f + g : A ∩ B → R
(f + g)(x) = f(x) + g(x)
Örneğin; (f + g)(2) = f(2) + g(2)
Fonksiyonlarla Çıkarma İşlemi
f : A → R ve g : B → R olmak üzere, f ve g fonksiyonlarının birlikte tanımlı olduğu $x$ değerleri için;
f – g : A ∩ B → R
(f – g)(x) = f(x) – g(x)
Örneğin; (f – g)(2) = f(2) – g(2) olur.
Fonksiyonlarla Çarpma İşlemi
f : A → R ve g : B → R olmak üzere, f ve g fonksiyonlarının birlikte tanımlı olduğu x değerleri için;
f * g : A ∩ B → R
(f * g) = f(x) * g(x)
Örneğin; (f * g)(4 )= f(4) * g(4) olur.
Fonksiyonlarla Bölme İşlemi
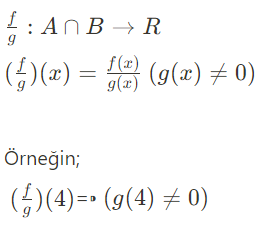
Fonksiyon Sayısı
A ve B iki küme olmak üzere s(A)=a, s(B)= b olsun:
- A’dan B’ye tanımlanan fonksiyon sayısı b^ a dır.
- A’dan B’ye tanımlanan fonksiyon sayısı {a!} / {(b-a)! dir.
- A’dan B’ye tanımlanabilecek sabit fonksiyon sayısı b’dir.
Fonksiyonların Grafikleri ve Grafik Okuma
Fonksiyon bağıntısının elemanlarının her birinin koordinat düzleminde grafik ile gösterilmesine fonksiyon grafiği denir. Bir grafiğin fonksiyon olup olmadığını anlayabilmek için dikey doğru testi uygulanır. Grafiğin fonksiyon olabilmesi için, çizilen her bir dikey çizgi grafiği yalnız bir noktada kesmelidir. Grafiği bir noktada kesmeyen veya birden fazla noktada kesen çizgi varsa bu grafik fonksiyon değildir.
Fonksiyon ile İlgili Gerçek Hayat Problemleri
30 soruluk bir sınavda 4 yanlış bir doğruyu götürmektedir. Boş bırakılmayan sınavda n adet soruyu doğru cevaplayan bir öğrencinin net sayısını veren fonksiyon nedir?
Öncelikle örnek bir net hesaplayabilmek için doğru ve yanlışa birer değer verelim
Doğru: 18
Yanlış: 12
Net: ?
4 yanlış bir doğruyu götürüyor ise 12 yanlış 12/4’ten 3 doğruyu götürür.
Net sayısı ise 18-3=15 şeklinde bulunur.
Bu durumda n tane soruyu doğru cevaplayan bir öğrencinin;
Doğru sayısı = n
Yanlış sayısı = 30 – n
Net Sayısı = {30-n} / {4}‘ün doğru sayısından çıkarılması ile elde edilir.
n – {30-n} / {4}

