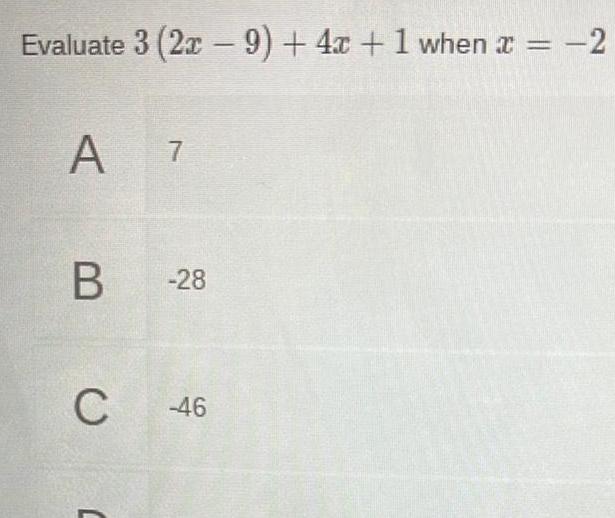
Algebra Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.



Algebra
Matrices & DeterminantsA corporation creates a sinking fund in order to have 510 000 to replace some machinery in 10 years How much should be placed in this account at the end of each week if the annual interest rate is 3 2 compounded weekly Round your answers to the nearest cent How much interest would they earn over the life of the account Determine the value of the fund after 2 4 and 6 years 2 years 4 years 6 years es How much interest was earned during the third week of the 5th year

Algebra
Sequences & SeriesClearly A A a b 1 H H a b 1 1 H H a b A A H H ab G G G G A A H H H H 1 1 Also 0 A A H H 3ab 31 16 17 H 2a b and 22 1 6 1 4 200 3ab a b 1 2b a 2a b 3ab 2b a 2a b 9ab Let P n 25 1 24 n 5735 For n 1 P 1 625 24 5735 6336 24 x 11 which is divisible by 24 Hence P 1 Is true Let P K be the true where K 2 1 25 24 K 5735 24 2 where AEN For n k 1 For x 0 cot x sin P K 1 25 2 24 K 5735 25 25 1 24 K 5735 25 24 K 25 5735 5735 24 K 1 25 24 2 24 K 5735 24 24 25 24 24 K 24 5736 25 24 24 K 24 239 24 2 25 K 230 which is divisible by 24 Hence by the method of mathematical Induction result is true vne N and

Algebra
Quadratic equationsTwo companies working together can clear a parcel of land in 30 hours Working alone it would take Company A 3 hours longer to clear the land than it would Company B How long would it take Company B to clear the parcel of land alone Round your answer to the nearest tenth

Algebra
Quadratic equationsA rectangular dining room table is twice as long as it is wide If the perimeter of the table is 192 inches what is the width 64 inches 32 inches 47 inches 48 inches
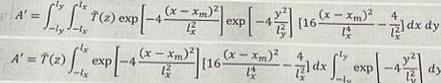
Algebra
Matrices & Determinantsx x A 1 2 xp 4 m exp 42 16 x Xm 1dx dy 1 T 2 exp 4 x 1m 11 4 x xm x xm 16 71dx exp 477 dx dy 1

Algebra
Permutations and CombinationsB4 Identity Laws XVO x XAI x B5 Complementation Laws x X 0 x V x I We write this algebraic structure as B X V A 0 1 or simply B if the context makes the meaning of tlie other terms clear The two operations V and A are called the join operation and meet operation respectively The unary operation is called the complementation From our discussion preceding the definition above you would agree that the set S of propositions is a Booleaii algebra where T and F will do the job of I and O respectively Thus S A V F T is an example of a Boolean algebra We give another example of a Boolean algebra below Example 1 Let X be a non empty set and P X denote its power set i e P X is the set consisting of all the subsets of the set X Show that P X is a Boolean algebra Solution We take the usual set theoretic operations of intersection n union u and complementation in P X as the three required operations Let and X play the roles of O and I respectively Then from MTE 04 you can verify that all the coriditions for P X U n X to be a Boolean algebra hold good For instance the identity laws B4 follow from two set theoretic facts hamely the intersection of any subset with the whole set is the set itself arid the union of any set with the empty set is the set itself On the otlier hand the complementation laws B5 follow from another set of facts from set theory namely the intersection of any subset with its complement is the empty set and the union of any set with its complement is the whole set Yet another example of a Boolean algebra is based on switching circuits For this we first need to elaborate on the functioning of ordinary switches in a mathematical way In fact we will present the basic ides which helped tlic American C E Shannon to detect tlic connection between the functioning of switches and Boole s symbolic logic You may be aware of the functioning of a simple on off switch which is commonly used as an essential component in the electric or electronic networking systems A switch is a clevice which allows the current to flow only when it is placed in tlic ON position i e when the gap is closed by a conducting rod Thus the ON position of a switch is one state of a switch called a closed state The other state of a switch is the open state when it is placed in the OFF position So a switch has two stable states There is another way to talk about the functioning of a switch We can denote a switch by x and use the values 0 and 1 to depict its two states i e to convey that x is open we write x 0 and to convey that x is closed we write x 1 see Fig 2 TXT These values which clcnote the state of a switch x are called the state values s v in short of that switch Boolean Algebra Circ x 1 x 0 Fig 2 OFF ON p tion

Algebra
Permutations and Combinationsthis definition Now using Tables 1 and 2 you can check that the five laws B1 B5 hold good Thus S par ser 1 0 1 is a Boolean algebra A Boolean algebra whose underlying set has only two elements is very important in the study of circuits We call such an algebra a two element Boolean algebra Throughout the unit we denote this algebra by B From this Boolean algebra we can build many more as in the following example Example 3 Let B BxBx x B e e2 en each e 0 or 1 for n 2 1 be the Cartesian product of n copies of B For ik jk 0 1 1 k n define 11 12 11 12 1 2 Jn i1Aj1 12 A 12 in jn Vi1 j2 11 12 in El a Then B is a Boolean algebra for all n 1 Solution Firstly observe that the case n 1 is the Boolean algebra B Now let us write 0 0 0 0 and I 1 1 1 for the two clcments of B consisting of n tuples of 0 s and 1 s respectively Using the fact that B is a Boolean algebra you can check that B3 with operations as clcfined above is a Boolean algebra for every n 2 1 in Vj1 12 Vj2 in Vin and The Boolean algebras B 121 called switching algebras are very useful for the study of the hardware and software of digital computers We shall now state without proof some other properties of Boolean algebras which can be deduced from the five laws B1 B5 Theorem 1 Lot B S V A O I be a Boolean algebra Then the following laws hold Vx y ES x V x x x Ax x a Idempotent laws b Absorption laws c Involution law d De Morgan s laws x V x Ay x x A XV y x x x xVy x Ay x Ay x Vy In fact you have already come across some of these properties for the Boolean algebra S of propositions in Unit 1 In the following exercise we ask you to verify them Verify the identity laws and absorption laws for the Boolean algebra S A V T F of propositions b Verify the absorption laws for the Boolean algebra P X U n X 1 In Theorem 1 you may have noticed that for each statement involving V and A there is an analogous statement with A instead of V and V instead of A This is not a coincidence as the following definition and result shows Definition Ifp is a proposition involving A and V the dual of P denoted by pd is the proposition obtained by replacing each occurrence of A and or V in p by V and or A respectively in p For example x V x A y x is the dual of x A x V y x Boolean A

Algebra
Permutations and CombinationsNow you should find it easy to solve the following exercise E4 Simplify tlie Boolean expression X X1 X2 X3 x1 A X2 V X1 AX2 A X3 V X2 AX3 With this we conclude this section In the next Section we shall give an important application of the concepts discussed here 3 4 LOGIC CIRCUITS If you loole around you would notice many electric or electronic appliances of daily use Sorne of them need a sirnple switching circuit to control the auto stop such as in a stereo system Some would use an auto power oil systeni used in transformers to control voltage fluctuations Each circuit is usually a combination of on off switches wirecl together in some specific configuration Nowadays certain types of electronic blocks i e solid state devices such as transistors resistors and capacitors are more in usc We call these electronic bloclcs logic gates or simply gates In Fig 5 we have shown a box which consists of some electronic switches or logic gates wired together in a specific manner Each line which is entering tlie box from the left represents an independent power source called input where all of them need not supply voltage to tlie box at a given moment A single line coming out of the box gives tlie final output of the circuit box The output depends on the type of input Input power lines Circuit Box Output lead Fig 5 A logic circuit This sort of arrangement of input power lines a circuit box and output lead is basic to all electronic circuits Throughout tlic unit any sucli interconnected assemblage of logic gates is referred to as a logic circuit As you may know computer hardwares are designed to handle only two levels of voltage both as inputs as well as outputs These two levels denoted by 0 and 1 are called bits an acronym for binary digits When the bits are applied to the logic gates by means of one or two wires input leads tlie output is again in the form of voltages 0 and 1 Roughly speaking you may think of a gate to be on or off according to whether the output voltage is at level 1 or 0 respectively Three basic types of logic gates are an AND gate an OR gate and a NOT gate We shall now define them one by one Definition Let the Boolean variables x and x2 represent any two bits An AND gate receives inputs x arid x2 and produces the output denoted by xi A x2 as given in Table 3 alongside The standard pictorial representation of an AND gate is shown in Fig 6 From the first three rows of Table 3 you can see that whenever the voltage in any one of the input wires of the AND gate is at level 0 then the output voltage of the gate is also at level 0 Boolean Algebra a Circu Table 3 Output X1 0 0 AND gat X2 X1 X2 0 0 1 1 0 0 0 1

Algebra
Matrices & DeterminantsEary Logic ve means lements of a set of previousely ements of the Now the following principle tells us that if a statement is proved true then we have simultaneously proved that its dual is true If s is a theorem about a Theorem 2 The principle of duality Boolean algebra then so is its dual s It is because of this principle that the statements in Theorem 1 look so similar Let us now see how to apply Boolean algebra methods to circuit design For this purpose we shall introduce the necessary mathematical terminology and ideas in the following section 3 3 BOOLEAN EXPRESSIONS In Unit 2 you learnt how a compound statement can be formed by combining some propositions P1 P2 Pn say with the help of logical connectives A V and Analogously while expressing circuits mathematically we identify each circuit in terms of some Boolean variables Each of these variables represents either a simple switch or an input to some electronic switch Definition Let B X V A 0 1 be a Boolean algebra A Boolean expression in variables X1 X2 xk say each taking their values in the set X is defined recursively as follows i Each of the variables x x2 xk as well as the elements O and I of the Boolean algebra B are Boolean expressions ii If X and X are previously definecl Boolean expressions then X A X2 X V X2 and X are also Boolean expressions For instance x A x3 is a Boolean expression because so are x and x3 Similarly because x V x2 is a Boolean expression so is x1 V x2 A x AX3 If X is a Boolean expression in n variables x x2 Xn say we write this as X X X X Each variable x and its complement x 1 i k is called a literal For example in the Boolean expression X X1 X2 X3 x1 V x2 x1 X3 there are three literals namely X1 X2 and x3 In the context of designing a circuit or redesigning a circuit with fewer electronic switches we need to consider techniques for minimising Boolean expressions In the process we shall be using the concepts defined below Definition A Boolean expression in k variables x x2 xk is called a minterm if it is of the form y A y2 A Ayki i ii a maxterm if it is of the form y Vy2 V Vyki where each yj is a literal i e it is either an x or an x for 1 i k and Vi y for i j Thus a minterm or a maxterm in k variables is a meet or a join respectively of exactly k distinct variables For example X A x2 and x V x2 is a minterm a maxterm respectively in the two variables X and x2 Definition A Boolean expression involving k variables is in disjunctive

Algebra
Permutations and Combinationsas an arbitrary even number arid not a particular value Why don t you try an exercise ngw E6 Give a direct proof of the statement If x is a real number such that x 9 then either x 3 or x 3 Let us now consider another proof strategy 2 3 2 Indirect Proofs In this sub section we shall consider two roundabout methods for proving p q Proof by contrapositive In the first method we use the fad that the proposition p q is logically equivalent to its contrapositive q p i e p q q p For instance If Ammu does not agree with communalists then she is not orthodox is the same as If Ammu is orthodox then she agrees with communalists Because of this equivalence to prove p q wc can instead prove q p This means that we can assume that q is true and then try to prove that p is true In other words what we do to prove p q in this method is to assume that q is false and then show that p is false Let us consider an example Example 4 Prove that If x y EZ such that xy is odd then botli x and y are odd by proving its contrapositive Solution Let us name the statements involved as below P xy is odd q both x and y are odd So p xy is even and q x is even or y is even or both are even We want to prove p q by proving that q p So we start by assuming that q is true i c we suppose that x is even Then x 2ii for some n E N Therefore xy 2ny Therefore xy is even by definition That is p is true So we have shown that q p Therefore p q S f Why don t you try some related exercises now E7 Write down the contrapositive of the statement If f is a 1 1 function from a finite set X into itself then f must be surjective E8 Prove the statement If x is an integer and x is even then x is also even by proving its contrapositive And now let us consider the other way of proving a statement indirectly

Algebra
Permutations and Combinations2 3 DIFFERENT METHODS OF PROOF In this section we shall consider three different strategies for proving a statement We will also discuss a method that is used only for disproving a statement Let us start with a proof strategy based on the first rule of inference that we discussed in the previous section 2 3 1 Direct Proof This form of proof is based entirely on modus ponens Let us formally spell out the strategy Definition A direct proof of p q is a logically valid argument that begins with the assumption that p is true and in one or more applications of the law of detachment concludes that q must be true So to construct a direct proof of p q we start by assuming that P is true Then in one or more steps of the form p 9 9192 9n q we conclude that q is true Consider the following examples 1 Example 2 Give a direct proof of the statement The product of two odd integers is odd Solution Let us clearly analyse what our hypotheses are and what we have to prove We start by considering any two odd integers x and y So our hypothesis is p x and y are odd The conclusion we want to reach is q xy is odd 9 Let us first prove that P Since x is odd x 2m 1 for some integer m Similarly y 2n 1 for some integer n Then xy 2m 1 2n 1 2 2mn m n 1 Therefore xy is odd So we have shown that p q Now we can apply modus ponens to p A p q to get the required conclusion Note that the essence of this direct proof lies in showing p q b Exar 3 Give a direct proof of the theorem The square of an even integer is an even integer Solution First of all let us write the given statement symbolically as VxEZ p x q x where p x x is even and q x x is even i e q x is the same as p x The direct proof then goes as follows Let x be an even number i e we assume p x is true Then x 2n for some integer n we apply the definition of an even number

Algebra
Matrices & Determinantslikely to turn around look menacingly at me and say Prove it What she or he really wants is to be convinced of my statement by some evidence In this case it would probably be a big physical push Convincing evidence is also what the world asks for before accepting a scientist s predictions or a historian s claims In the same way if you want a mathematical statement to be accepted as true you would need to provide mathematically acceptable evidence to support it This means that you would need to show that the statement is universally true And this would be done in the form of a logically valid argument Definition An argument in mathematics or logic is a finite sequence of statements P P p such that p A P A A p p Each statement in the sequence except the last one i e pi for i 1 n is called a premise or an assumption or a hypothesis The final statement p is called the conclusion Let s consider an example of an argument that shows that a given statement is true Example 1 Give an argument to show that the mathematical statement For any two sets A and B An BCA is true Solution One argument could be the following Let x be an arbitrary element of AnB Then X E A and x E B by definition of n Therefore x A This is true for every x in An B Therefore AnBC A by definition of C The argument in Example 1 has a peculiar nature The truth of each of tho 4 premises and of its conclusion follows from the truth of the earlier premises in it Of course we start by assuming that the first statement is true Then assuming the definition of intersection the second statement is true Tlic third one is true whenever the second one is true because of the properties of logical implication The fourth statement is truc whenever the first three arc true because of the definition and properties of the term for all And finally the last statement is true whenever all the earlier ones are In this way we have shown that the given statcinent is true In other words we have proved the given statement as the following definitions show Definitions We say that a proposition p follows logically from propositions P P2 and Pn if p must be true whenever P P2 Pn are true i e P AP A AP p Here note the use of the implication arrow For any two propositions r and s rs denotes s is true whenever r is true Note that using the contrapositive this also denotes r is false whenever s is false Thus rs and rs are different except when both r and s are true or both are false A proof of a proposition p is a mathematical argument consisting of a sequence of statements P P2 Pn from which p logically follows So p is the conclusion of this argument The statement that is proved to be true is called a theorem Sometimes as you will see in Sec 2 3 3 instead of showing that a statement p is true we try to prove that it is false i e that p is true Such a proof is

Algebra
Quadratic equationsthe conclusion is true Therefore the argument is valid This form of valid argument is called the law of detachment because the conclusion q is detached from a premise namely p q It is also called the law of direct inference ii Law of contraposition or modus tollens To understand this law consider the following argument If Kali can draw then she will get a job Kali will riot get a job Therefore Kali can t draw Taking p arid q as in i above you can see that the premises arc p q and q The conclusion is p So the argument is P q 9 P If you check you ll find that this is a valid form of argument There are two more rules of inference that most commonly form tlie basis of several proofs The following exercise is about them 3 E4 You will find three arguments below Convert each of them into the language of symbols and check if they are valid i Either the eraser is white or oxygen is a metal The eraser is black Therefore oxygen is a metal i c pq Aq p ii If Madhu is a sarpanch she will head the panchayat If Madhu heads the panchayat she will decide on property disputes Therefore if Madhu is a sarpanch she will decide on property disputes iii Either Munna will cook or Mumi will practise Karate If Munni practises Karate then Munna studies 1 Munna does not study Therefore Munni will practise Karate E5 Write down one example each of modus ponens and modus tollens As you must have discovered the arguments in E4 i and ii arc valid The first one is an example of a disjunctive syllogism The second one is an example of a hypothetical syllogism Thus a disjunctive syllogism is of the form pvq P i e pv q Ap q q And a hypothetical syllogism is of the form 2 P q qr i e p q qr pr Method Modus tollen method of de

Algebra
Matrices & Determinantscalled a disproof of p In the next section you will read about some ways of disproving a statement Sometimes it happens that we feel a certain statement is true but we don t succeed in proving it It may also happen that we can t disprove it Such statements are called conjectures If and when a conjecture is proved it would be called a theorem If it is disproved then its negative will be a theorem In this context there s a very famous conjecture which was made by a mathematician Goldbach in 1742 He stated that For every n E N if n is even arid n 2 then n is the sum of two primes To this day no one has been able to prove it or disprove it To disprove it several people have been hunting for an example for which the statement is not truc i e an even number 1 2 such that h cannot be written as the sum of two prime numbers Now as you have seen a mathematical proof of a statement consists of one or more premises These premises could be of four types i a proposition that has been proved earlier e g to prove that the complex roots of a polynomial in R x occur in pairs we use tlie division algorithm or ii a proposition that follows logically from the earlier the proof as you have seen in Example 1 or iii a mathematical fact that has never been proved but is universally accepted as true e g two points determine a line Such a fact is called an axiom or a ppstulate Dositions given in iv the definition of a mathematical term e g assuming the definition of C in the proof of AnBCA You will come across more examples of each type while doing the following exercises and while going through proofs in this course and other courses El Write down an example of a theorem and its proof of at least 4 steps taken from school lcvcl algebra At each step indicate which of tlie four types of premise it is E2 Is every statement a theorem Why So far we have spoken about valid or acceptable arguments Now let us see an example of a sequence of statements that will not Sorm a valid argument Consider the following sequence If Maya sees the movie she won t finish her homework Maya won t finish her homework Therefore Maya sees the movie Looking at the argument can you say whether it is valid or not Intuitively you may feel that the argument isn t valid But is there a formal logical tool that you can apply to checlr if your intuition is correct What about truth tables Let s see The given argument is of the form pa q P where p Maya sees the movie and q Maya won t finish her homework J M

Algebra
Permutations and Combinationsns 1 P i T TTT F T 1 F Table 1 qpq p a A p T F T F F F 1 The last column gives the truth values of the premises The first column gives the corresponding truth values of the conclusion Now the argument will only be valid if whenever both the premises are true the conclusion is true This happens in the first row but not in the third row Therefore the argument is not valid Why don t you check an argument for validity now F T T E3 Check whether the following argument is valid pqV r q p pr You have seen that a proof is a logical argument that verifies the truth of a theorem There are several ways of proving a theorem as you will see in the next section All of them are based on one or more rules of inference which are different forms of arguments We shall now present four of the most commonly used rules Law of detachment or modus ponens Consider the following argument If Kali can draw she will get a job Kali can draw Therefore she will get a job To study the form of the argument let us take p to be the proposition Kali can draw and q to be the proposition Kali will get a job Then the premises are pq and p The conclusion is q So the form of the argument is P q P q Is this argument valid To find out let s construct its truth table see Table 2 Table 2 Truth table for p q A p q i e pq Ap q I P q P q pa p T T T T F F F T F F F T F In the table look at the second column the conclusion and the fourth T F CL

Algebra
Permutations and CombinationsSolution Let us start by assuming A is a truth teller What A says is true B is a truth teller What B says is true A and B are of opposite types This is a contradiction because our premises say that A and B are both truth tellers The assumption we started with is false A always tells lies What A has told you is a lie B always tells lies A and B are of the same type i e both of them always lie Here are a few exercises for you now While doing them you would realise that there are situations in which all the three methods of proof we have discussed so far can be used E9 Use the method of proof by contradiction to show that i 3 is irrational ii For x E R if x 4x 0 then x 0 6 E10 Prove E 9 ii directly as well as by the method of contrapositive E11 Suppose you are visiting the village described in Example 7 above Another two villagers C and D approach you C tells you Both of us always tell the trutli and D says C always lies What types are C and D Let us now consider the problem of showing that a statement is falsc 2 3 3 Counterexamples Suppose I make the statement All human beings are 5 feet tall You are quite likely to show me an example of a human being standing nearby for whom the statement is not true And as you know the moment we have even one example for which the statement Vx p x is false i e 3x p x is true then the statement is false An example that shows that a statement is false is a counterexample to such a statement The name itself suggests that it is an example to counter a given statement A common situation in which we look for counterexamples is to disprove statements of the form p q From Unit 1 you know that p q PA q Therefore a counterexample to p where p q is true i e p is true and holds but the conclusion q does not hold q needs to be an example q is true i e the hypothesis p For instance to disprove the statement If n is an odd integer then n is prime we need to look for an odd integer which is not a prime number 15 is one such integer So n 15 is a counterexample to the given statement Notice that a counterexample to a statement p proves that P is false i e p is true Let us consider another example Example 8 Disprove the following statement VaR VbER a b a b

Algebra
Permutations and Combinations4 5 Proof by contradiction In this method to prove q is true we start by assuming that q is false i e q is true Then by a logical argument we arrive at a situation where a statement is true as well as false i e we reach a contradiction r r for some statement r This means that the truth of q implies a contradiction a staternent that is always false This can only happen when q is false also Therefore q must be true This method is called proof by contradiction It is also called reductio ad absurdum a Latin phrase because it relies on reducing a given assumption to an absurdity Let us consider an example of the use of this method Example 5 Show that 5 is irrational Solution Let us try and prove the given statement by contradiction For this we begin by assuming that 5 is rational This rneans that there exist positive integers a and b such that 5 where a and b have no common a b factors This implies a 5b a 5b 5 a 5 a Therefore by definition a 5c for some c E Z Therefore a 25c But a 5b also So 25c 5b2 5c b 5 b 5 b AD But now we find that 5 divides both a and b which contradicts our e assumption that a and b have no common factor Therefore we conclude that our assumption that 5 is rational is false i e 5 is irrational We can also use the method of contradiction to prove an implication r s Here we can use the equivalence rs rAs So to prove r s we can begin by assuming that r s is false i e r is true and s is false Then we can present a valid argument to arrive at a contradiction Consider the following example from plane geometry Example 6 Prove the following If two distinct lines L and La intersect then their intersection consists of exactly one point Solution To prove the given implication by contradiction let us begin by assuming that the two distinct lines L and L2 intersect in more than one point Let us call two of these distinct points A and B Then both L and L2 contain A and B This contradicts the axiom from geomctry that says Given two distinct points there is exactly one line containing them Therefore if L and L2 intersect then they must intersect in only one point The contradiction rule is also used for solving many logical puzzles by discarding all solutions that reduce to contradictions Consider the following example those Example 7 There is a village that consists of two types of people who always tell the truth and those who always li Suppose that you visit the village and two villagers A and B come up to you Further suppose A says B always tells the truth and B says A and I are of opposite types What types are A and B 8

Algebra
Matrices & DeterminantsSolution A good way of disproving it is to look for a counterexample that is a pair of real numbers a and b for which a b2 but a b Can you think of such a pair What about a 1 and b 1 They serve the purpose In fact there are infinitely many counterexamples Why Now an exercise E12 Disprove the following statements by providing a suitable counterexample i VxEZ x N ii x y n x y Vn N x yeZ iii f N N is 1 1 iff f is onto Hint To disprove p q it is enough to prove that p q is false or qp is false There are some other strategies of proof like a constructive proof which you will come across in the appendix to Unit 11 and in other mathematics courses We shall not discuss this method here Other proof related adjectives that you will come across are vacuous and trivial A vacuous proof makes use of the fact that if p is false then p q is true regardless of the truth value of q So to vacuously prove pq all we need to do is to show that p is false For instance suppose we want to prove that If n n 1 for n Z then n 0 Since n n 1 is false for every ne Z the given statement is vacuously true or true by default Similarly a trivial proof of p q is one based on the fact that if q is true then pq is true regardless of the truth value of p So for example If n n 1 for n E Z then n 1 n is trivially true since n 1 nVnEZ The truth value of the hypothesis which is false in this example does not come into the picture at all Here s a chance for you to think up such proofs now E13 Give one example each of a vacuous proof and a trivial proof And now let us study a very important technique of proof for statements that are of the form p n n N 2 4 PRINCIPLE OF INDUCTION In a discussion with some students the other day one of them told me very cynically that all Indian politicians are corrupt I asked him how he had reached such a conclusion As an argument he gave me instances of several politicians all of whom were known to be corrupt What he had done was to formulate his general opinion of politicians on the basis of several particular instances This is an example of inductive logic a process of reasoning by which general rules are discovered by the observation of several individual

Algebra
Sequences & Series1 Use the integral test to determine if the series converge or diverge a 8 0 2 n n 1 b

Algebra
Matrices & Determinants7 of such a pair What about a 1 and b 1 They serve the purpose In fact there are infinitely many counterexamples Why Now an exercise E12 Disprove the following statements by providing a suitable counterexample i VxEZ x N ii x y n x y Vn N x y Z iii f N N is 1 1 iff f is onto Hint To disprove p q it is enough to prove that p q is false or qp is false There are some other strategies of proof like a constructive proof which you will come across in the appendix to Unit 11 and in other mathematics courses We shall not discuss this method here Other proof related adjectives that you will come across are vacuous and trivial A vacuous proof makes use of the fact that if p is false then p q is true regardless of the truth value of q So to vacuously prove p q all we need to do is to show that p is false For instance suppose we want to prove that If n n 1 for n Z then n 0 Since n n 1 is false for every ne Z the given statement is vacuously true or true by default Similarly a trivial proof of p q is one based on the fact that if q is true then p q is true regardless of the truth value of p So for example If n n 1 for n E Z then n 1 n is trivially true since n 1 nVnEZ The truth value of the hypothesis which is false in this example does not come into the picture at all Here s a chance for you to think up such proofs now E13 Give one example each of a vacuous proof and a trivial proof And now let us study a very important technique of proof for statements that are of the form p n n N 2 4 PRINCIPLE OF INDUCTION In a discussion with some students the other day one of them told me very cynically that all Indian politicians are corrupt I asked him how he had reached such a conclusion As an argument he gave me instances of several politicians all of whom were known to be corrupt What he had done was to formulate his general opinion of politicians on the basis of several particular instances This is an example of inductive logic a process of reasoning by which general rules are discovered by the observation of several individual cases Inductive reasoning is used in all the sciences including mathematics But in mathematics we use a more precise form

Algebra
Quadratic equationsSubtract the product of 2x 1 x 3 from the sum of 2x 4x 5 and x 9x 6 This gives x 2 x 2 r2 10x 4

Algebra
Complex numbersroblem 1 Let f x 3x x 2 Complete the following a Find the vertex of f x b Does f x have a maximum or a minimum Justify your answer c State the interval s where f x is increasing d State the interval s where f x is decreasing e Write f x in the form of f x a x h k f Sketch the graph of f x Label the vertex and two additional points on the graph yc include the x and y coordinates of all points and appropriately scale the axes to incl entire graph
Algebra
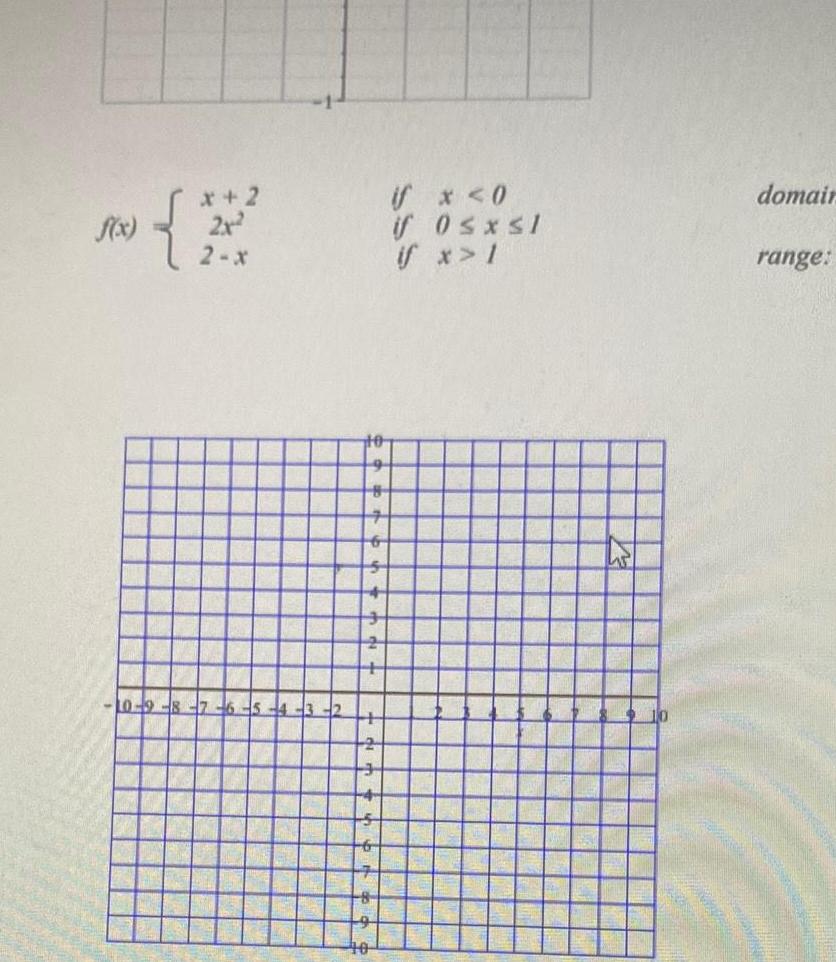
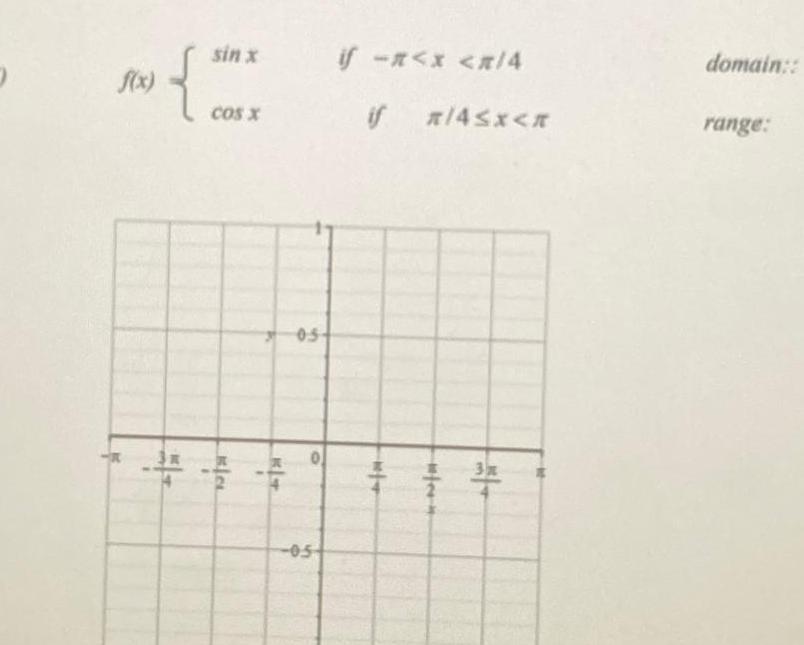
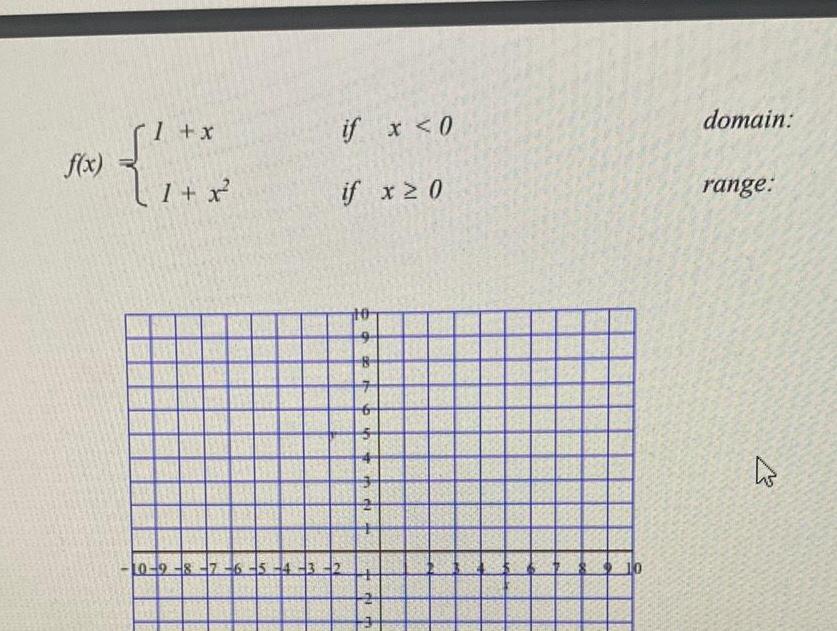
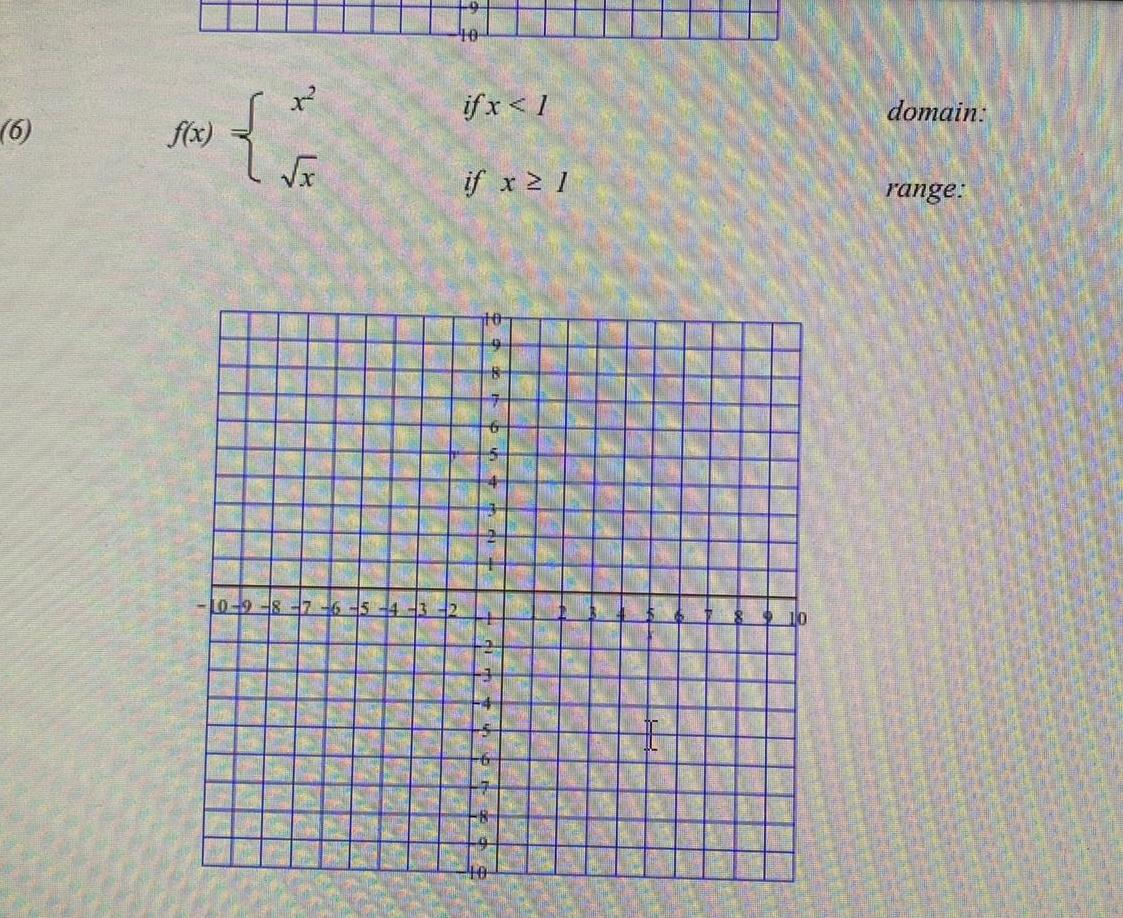
Quadratic equationsf x 1 x 1 x DAR BAR SUN MOD 100 10 9 7 6 5 4 m if x 0 if x 0 2 121 21 m 10 domain range K

Algebra
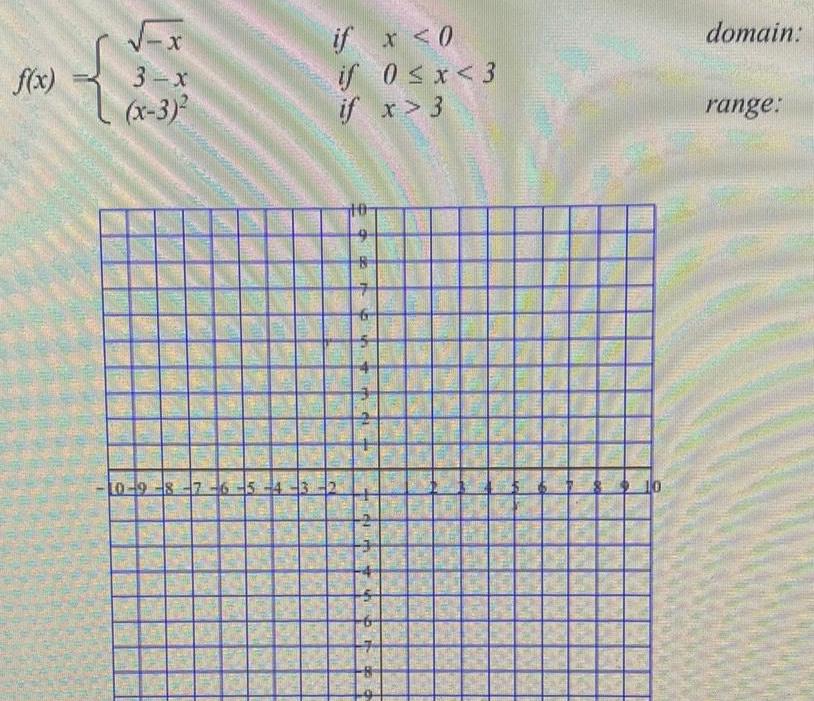
Quadratic equationsName GOZ 8 100 Prof Meangru The following functions were taken from Essential Calculus by James Stewart 2007 For each function 1 4 f x a Graph each function neatly b Describe the domain and range 1 x if x 1 if x 1 8 7 6 5 4 3 10 domain range
Algebra
Complex numbers6 f x x 2 fo x 10 9 8 7 6 5 4 3 2 10 if x 1 if x 1 4 8 tr N 10 10 domain range

Algebra
Quadratic equationsTo prove 1 2 2 l 1 z z 1 Zz z z Z Z 1 22 2 2 2 z 2 2 z 1 z 1 1 z 0 1 2 1 0 Which is obvious as z 1 z Pe cose 3 sine shortest distance exists along the common normal Slope of normal at P esece 3 cos ece 2 tan 6 1 so cose and sine 3 Hence PE 2 1 A A I a b c a b c bcabca ca bc a b 0 0 1 SOLUTIONS a b2 c ab bc ca ab bc ca 100 ab bc ca a b c ab bc ca 010 ab bc ca ab bc ca a 6 0 0 0 1 100 010 a b c 1 1 and ab bc ca 0 2 Now a b c a b c a b c ab bc ca 3abc a b c 3 3 Now a b c a b 2 ab bc ca 1 2 0 1 a b c 1 Now from 3 a b c 1 3 4 a b c 4 1 2 1 2 4 C 4C Alternate A A 1 AA A 1 a b c 3abc 1 a b c 3abc 1 since a b c are positive real number a b c 2 3abc from AM2 GM since a b c are real positive number 1 1 2 n k k r k r x y 7 n r n n r r n k k r
Algebra
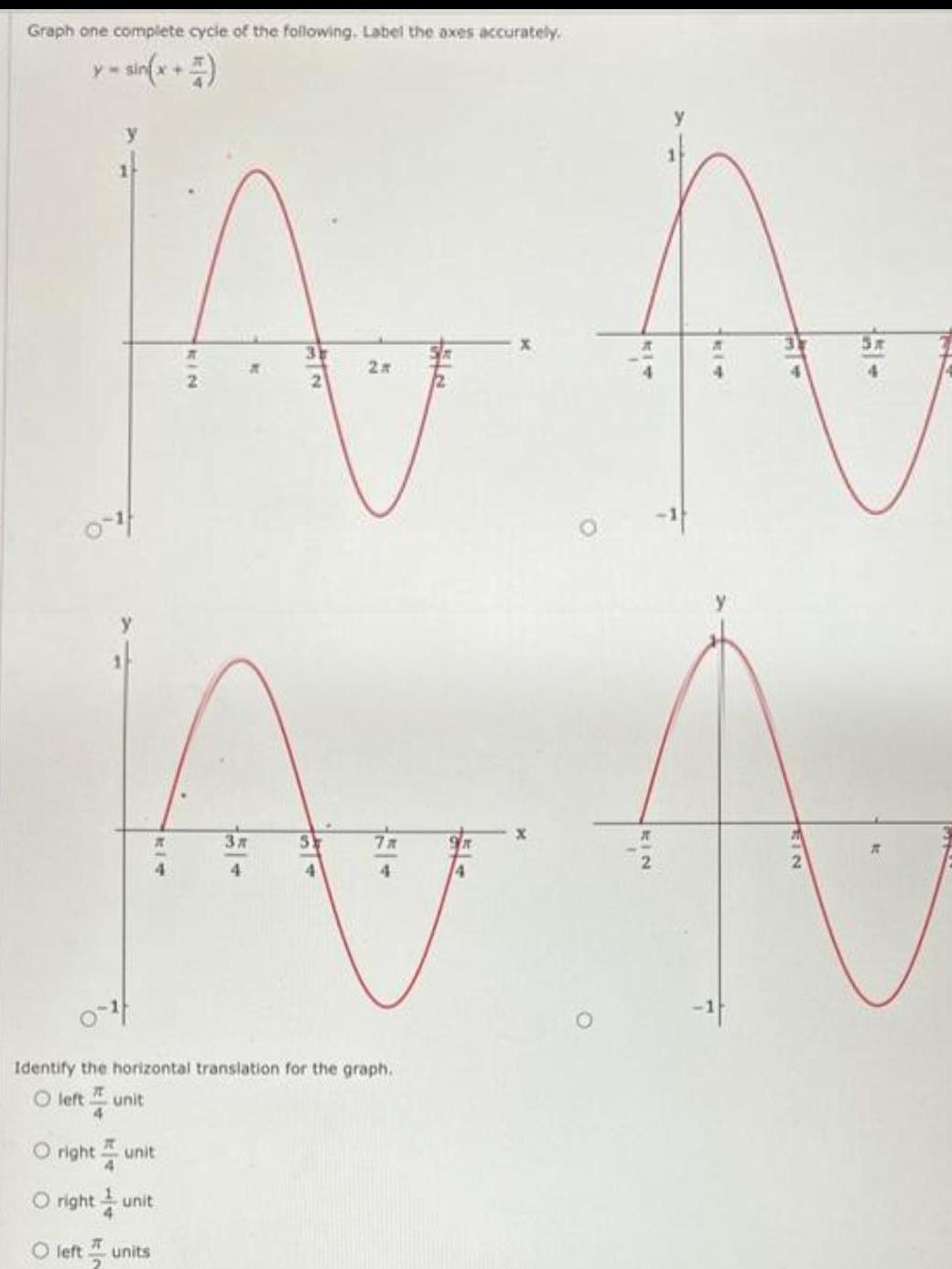
Quadratic equationsGraph one complete cycle of the following Label the axes accurately A A M A 3 7x 4 4 4 0 4 right unit O right unit O left units Identify the horizontal translation for the graph I Oleft unit 4 KIN EIN
Algebra
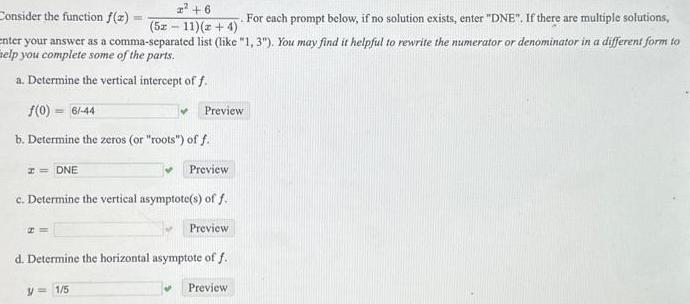
Complex numbers6 52 11 z 4 For each prompt below if no solution exists enter DNE If there are multiple solutions enter your answer as a comma separated list like 1 3 You may find it helpful to rewrite the numerator or denominator in a different form to elp you complete some of the parts a Determine the vertical intercept of f f 0 6 44 b Determine the zeros or roots off Consider the function f x I DNE 20 W V 1 5 Preview c Determine the vertical asymptote s of f Preview Preview d Determine the horizontal asymptote of f Preview
Algebra
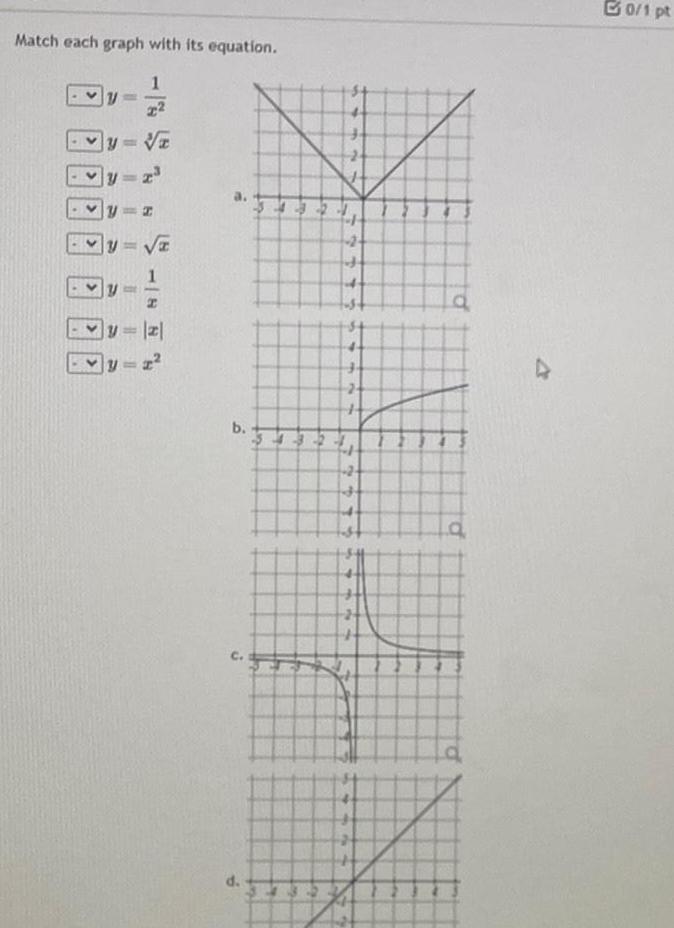
Quadratic equationsMatch each graph with its equation 1 x C Vz 1 GIF A 1 y z y z b d EZ Rad 13 2 0 1 pt
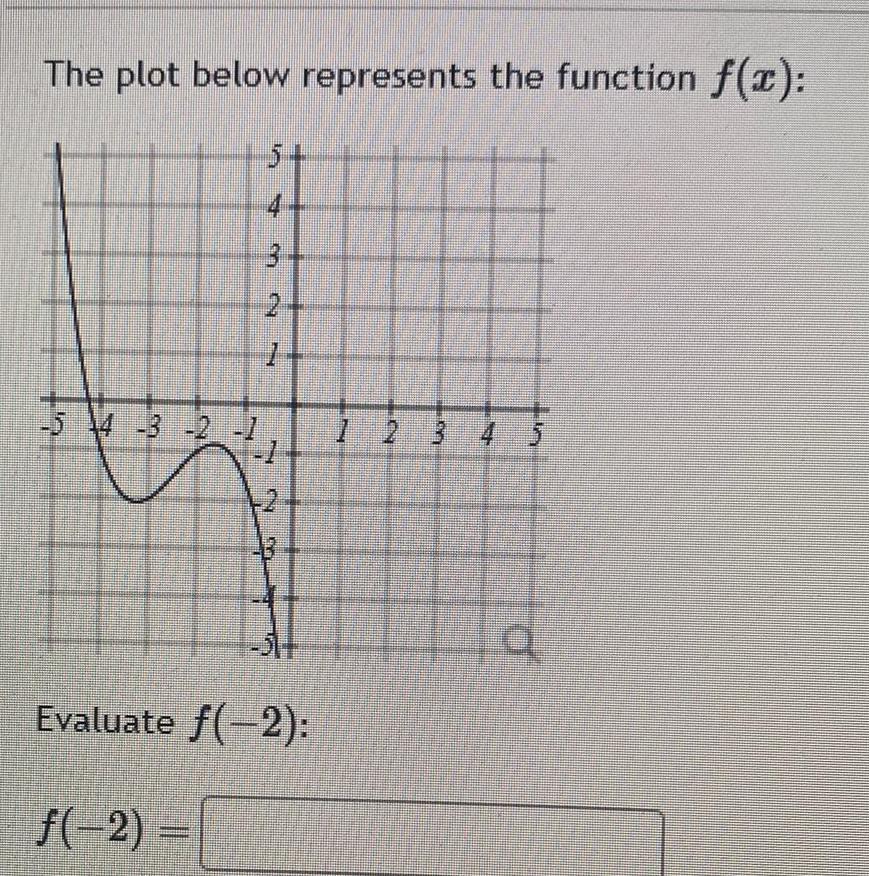
Algebra
Quadratic equationsThe plot below represents the function f x T 5 14 3 2 1 4 3 ba 2 7 hond 1 Evaluate f 2 f 2 1 2 3 4 LA 3 a
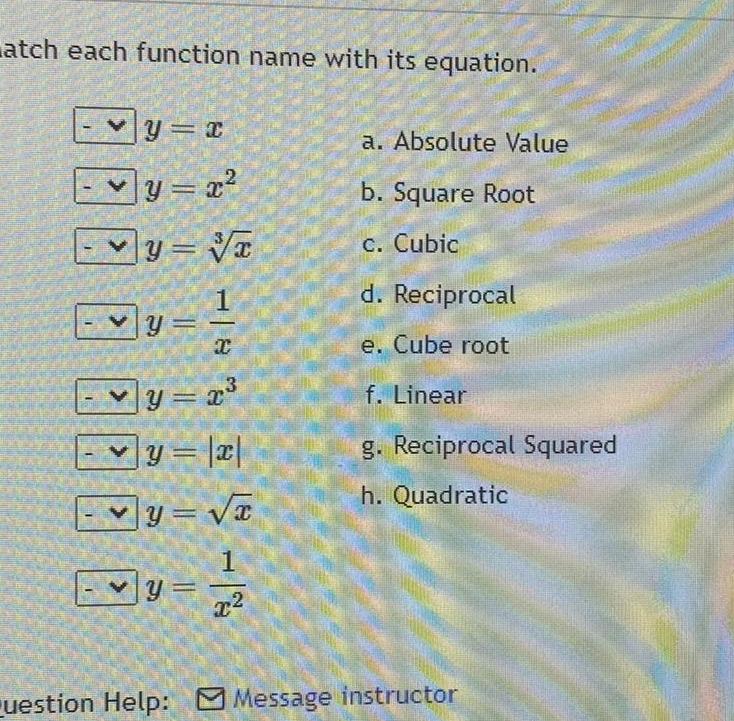
Algebra
Quadratic equationsatch each function name with its equation y x y x y x y y x y x y x 1 x 881 8 a Absolute Value b Square Root c Cubic d Reciprocal e Cube root f Linear g Reciprocal Squared h Quadratic Question Help Message instructor
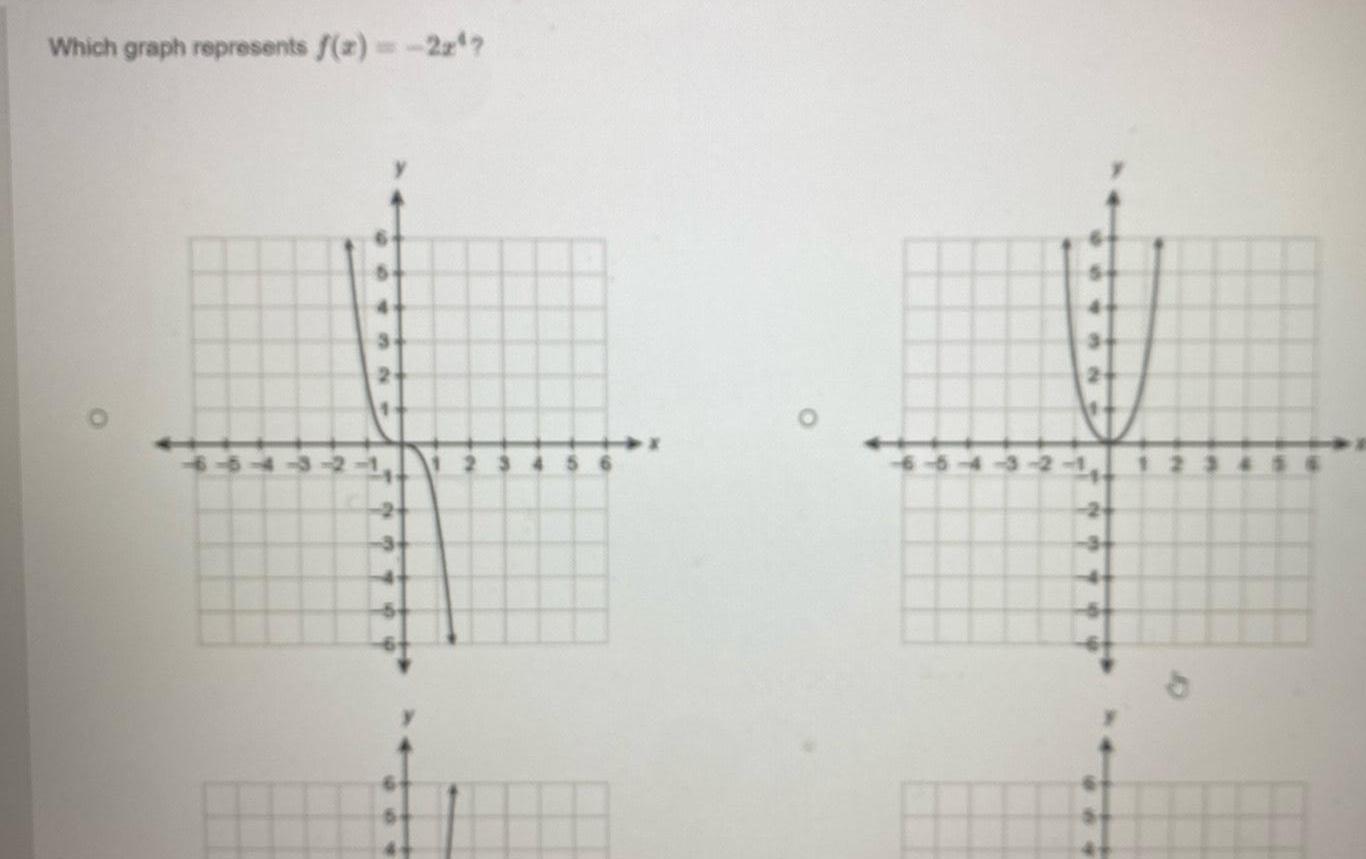
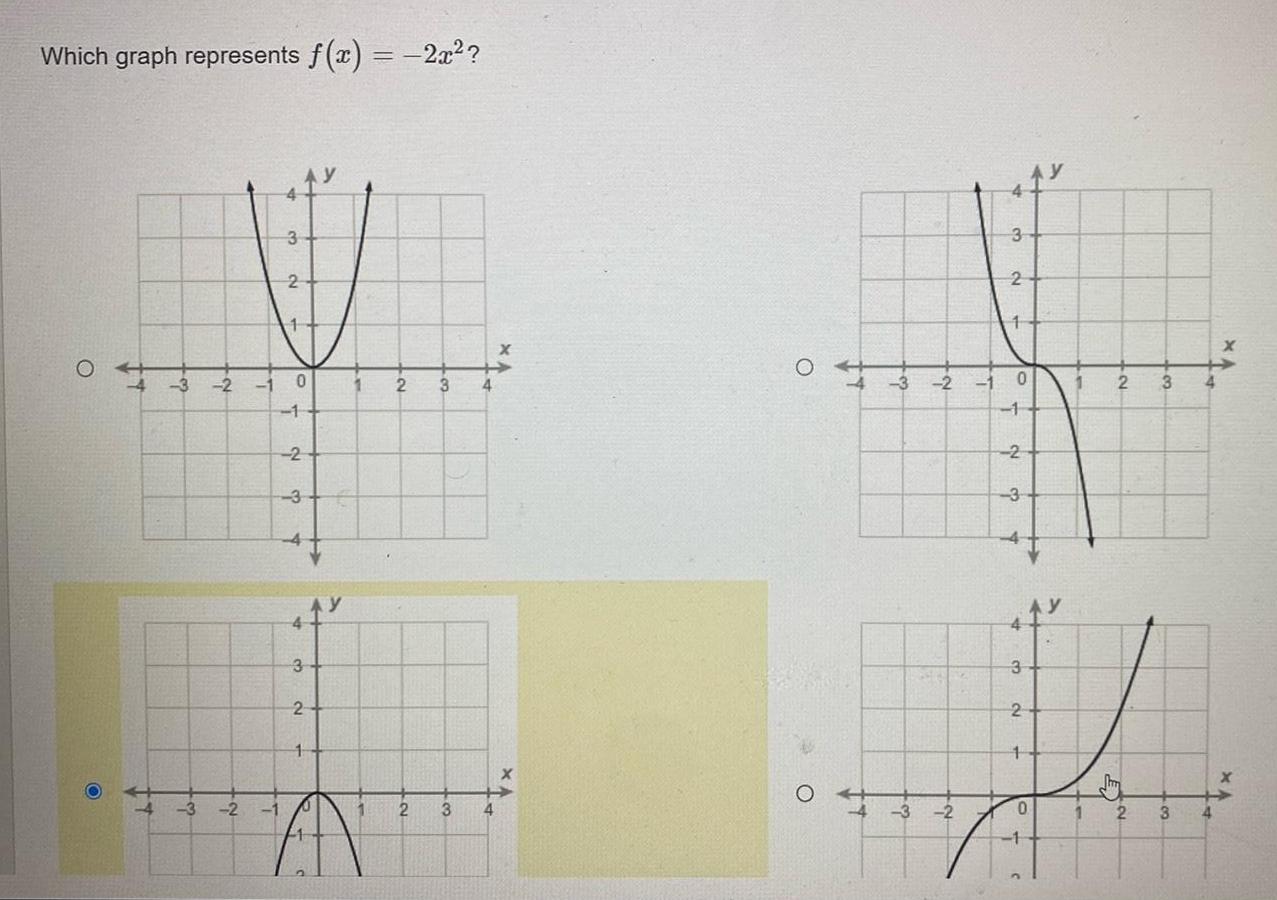
Algebra
Complex numbersWhich graph represents f x 2x 04321 3 2 3 2 NO 1 0 1 2 3 3 2 1 1 1 AN 2 2 3 3 4 4 X X O O 4 3 2 3 2 1 3 2 1 0 1 2 3 444 3 2 y 1 0 1 Ft 1 2 2 3 3 4 X
Algebra
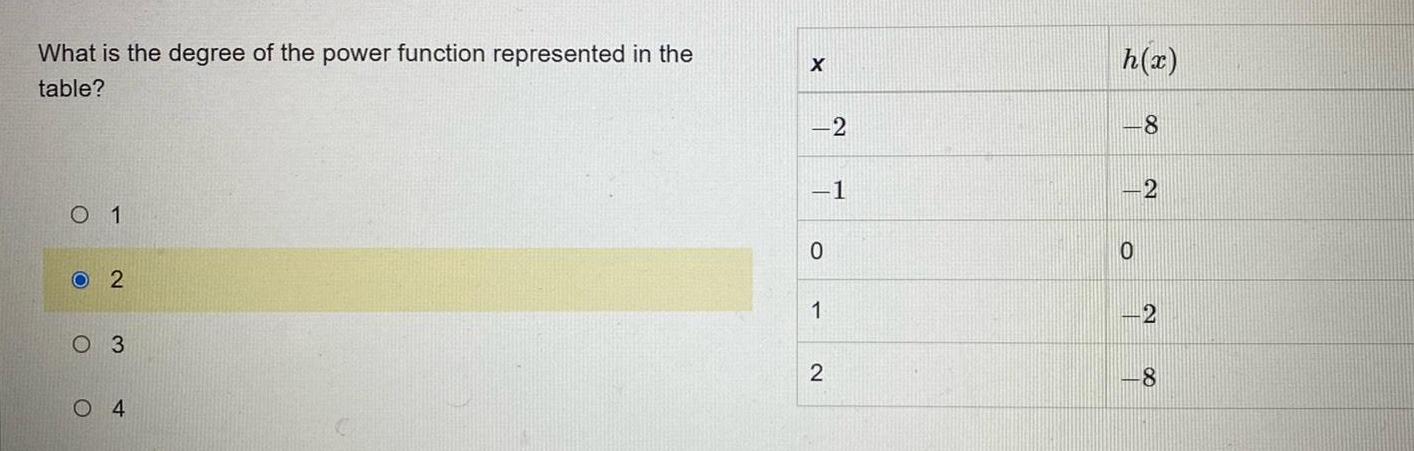
Complex numbersWhat is the degree of the power function represented in the table O 1 O 2 O 3 O4 X 1 0 1 2 2 h x 0 8 2 2 8

Algebra
Sequences & SeriesWhat is the remainder when the polynomial 8x2 4x 3 is divided by 2x 1 Enter your answer in the box

Algebra
Quadratic equationsWhat is the remainder when the polynomial 5x 10x Enter your answer in the box 15 is divided by x 5
Algebra
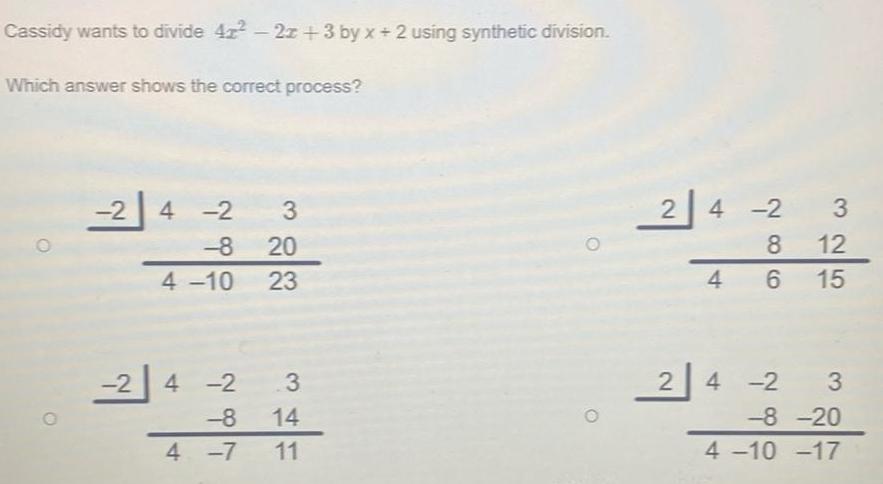
Quadratic equationsCassidy wants to divide 42 2z 3 by x 2 using synthetic division Which answer shows the correct process 2 4 2 3 8 20 4 10 23 2 3 4 2 8 14 4 7 11 2 4 2 8 4 6 24 2 3 12 15 4 2 3 8 20 4 10 17

Algebra
Complex numbersWhat is the result of dividing 7 by x 2 O x 2x 4 15 x 2 1 O x 2x 4 2 2 O x 2x 4 O 15 x 2 x 2x 4 z 2

Algebra
Quadratic equationsWhat is the result of dividing 2x 6x 6x 2 by x 1 2x 4x 10 2x 4x 2 O 2x 6x 2 2x 6x 12
Algebra
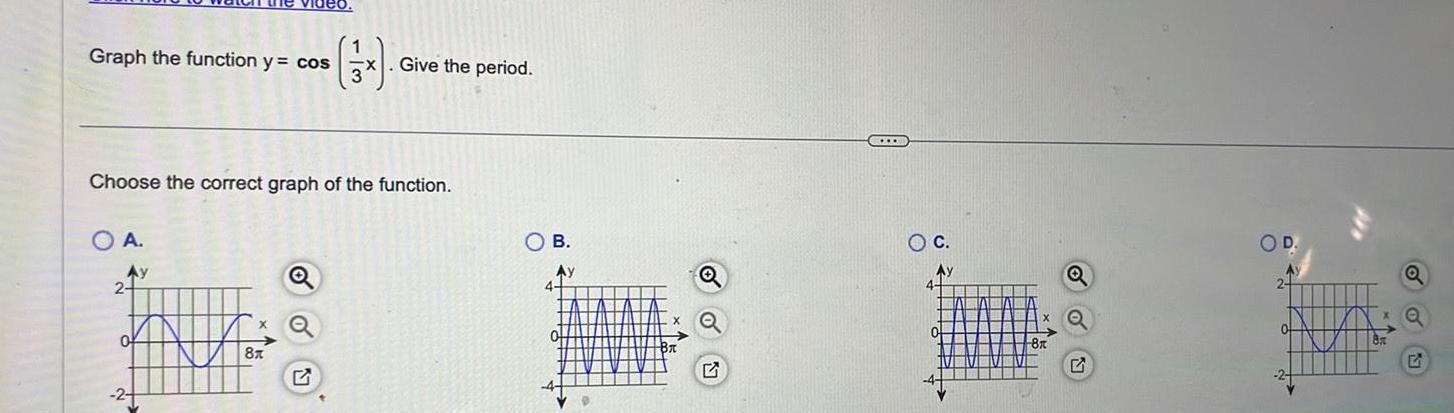
Quadratic equationsGraph the function y cos x Give the period Choose the correct graph of the function O A Ay 2 0 2 NA 8x Q OB Ay 4 0 B BA O C Ay 4 0 A 8x Q 5 OD M 2 8x Q 51
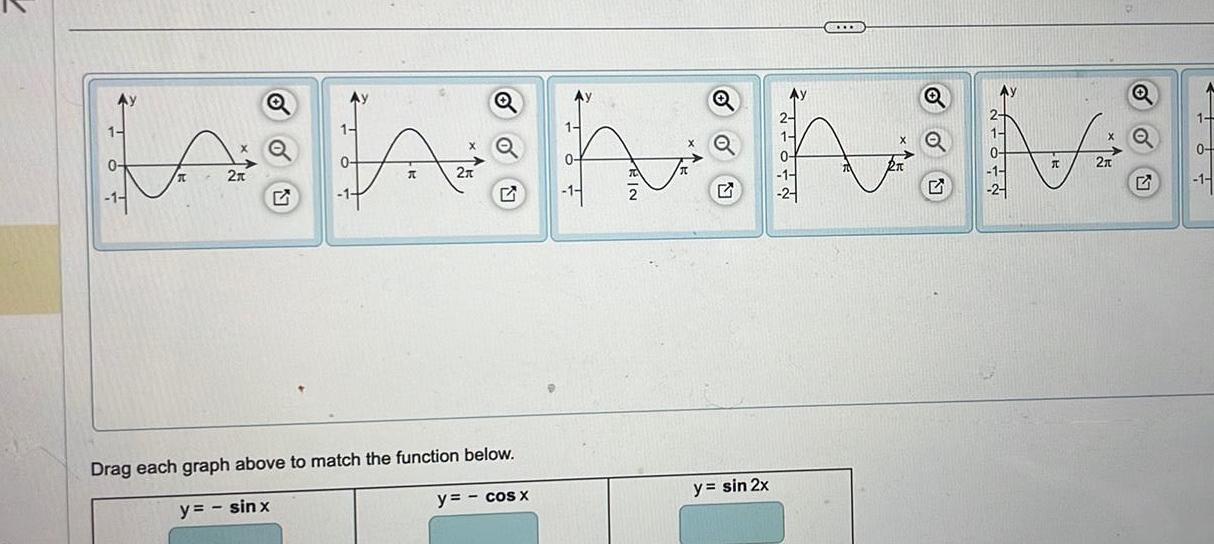
Algebra
Complex numbers1 2x 1 y sinx R 2x Drag each graph above to match the function below y cos x 1 y sin 2x Ay 2 1 2 T 2 1 0 1