Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Application of derivativesUse the Binomial Theorem to expand and simplify the expression a 7 4
Calculus
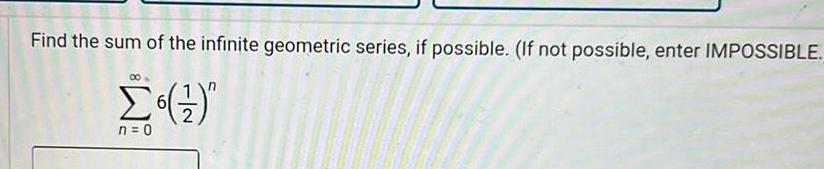
Limits & ContinuityFind the sum of the infinite geometric series if possible If not possible enter IMPOSSIBLE n 0


Calculus
Application of derivativesWrite an expression for the apparent nth term of the sequence Assume that n begins with 1 10 12 14 16 18 an 11
Calculus
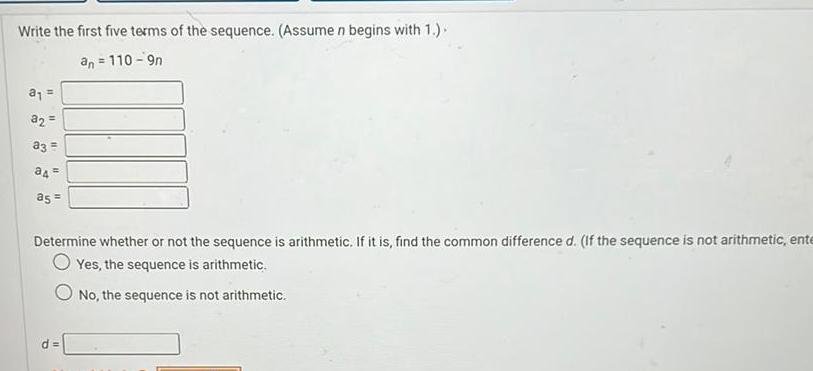
Vector CalculusWrite the first five terms of the sequence Assume n begins with 1 an 110 9n a 32 a3 a4 a5 Determine whether or not the sequence is arithmetic If it is find the common difference d If the sequence is not arithmetic ente O Yes the sequence is arithmetic No the sequence is not arithmetic d
Calculus
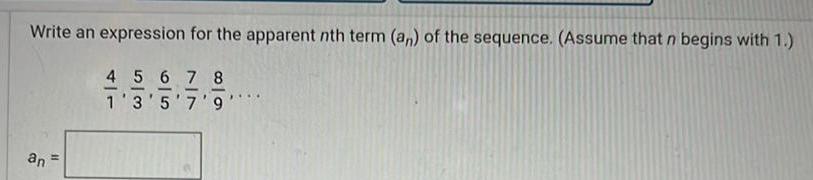
Application of derivativesWrite an expression for the apparent nth term an of the sequence Assume that n begins with 1 4 5 6 7 8 1 3 5 7 9 an 11
Calculus
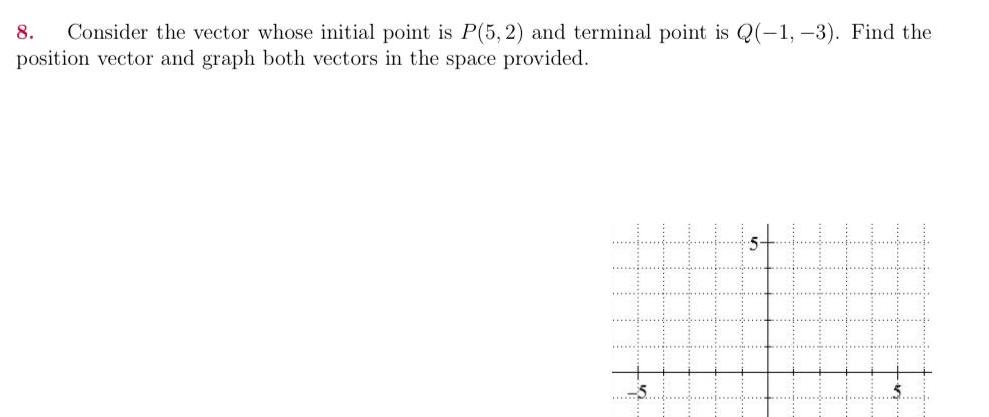
Vector Calculus8 Consider the vector whose initial point is P 5 2 and terminal point is Q 1 3 Find the position vector and graph both vectors in the space provided 5
Calculus
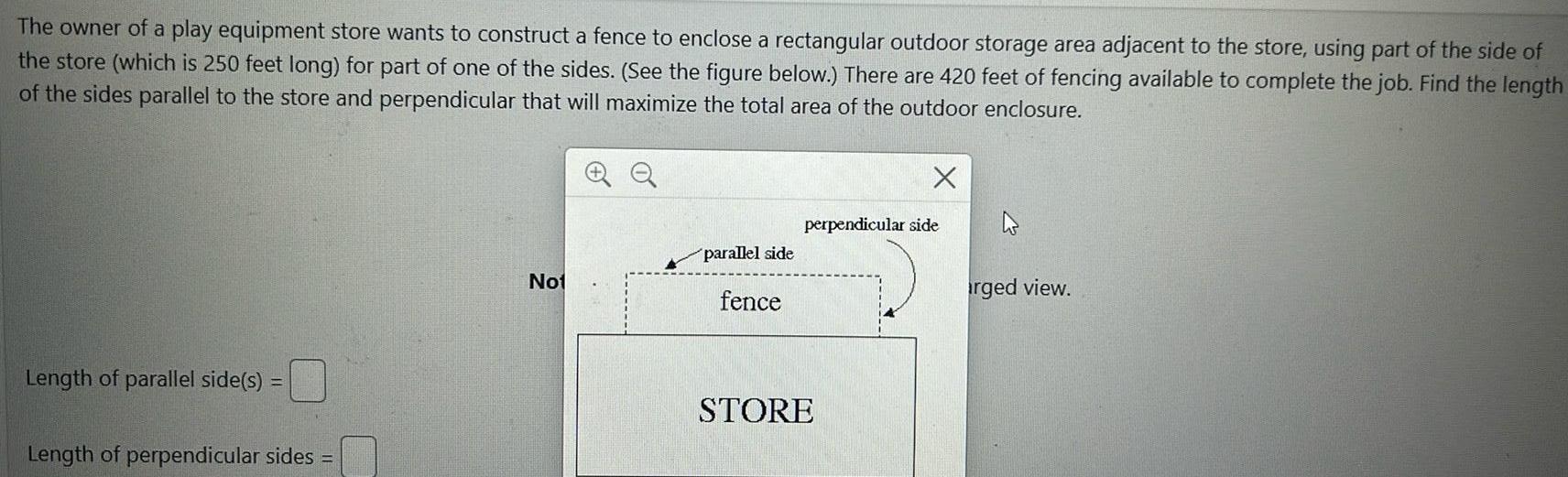
Application of derivativesThe owner of a play equipment store wants to construct a fence to enclose a rectangular outdoor storage area adjacent to the store using part of the side of the store which is 250 feet long for part of one of the sides See the figure below There are 420 feet of fencing available to complete the job Find the length of the sides parallel to the store and perpendicular that will maximize the total area of the outdoor enclosure Length of parallel side s Length of perpendicular sides Not parallel side fence X perpendicular side STORE rged view

Calculus
Limits & ContinuitySolve the logarithmic equation for x Enter your answers as a comma separated list log x log x 48 2 X

Calculus
Vector CalculusSolve the logarithmic equation for x as in Example 7 Enter your answers as a comma separated list 2 log x log 2 log 5x 8

Calculus
Vector Calculus7 To find the distance between two cities a satellite calculates the distance and the angle shown below not to scale Find the distance between the two cities Round your answer to the nearest tenth 250 km 1 8 210 km

Calculus
Vector CalculusSolve the logarithmic equation for x as in Example 7 Enter your answers as a comma separated list log x log x 3 log 3x X

Calculus
Application of derivativesA car rental agency rents 200 cars per day at a rate of 30 dollars per day For each 1 dollar increase in the daily rate 5 fewer cars are rented At what rate should the cars be rented to produce the maximum income and what is the maximum income Rate Maximum Income

Calculus
Differential equationsA rectangle is inscribed with its base on the x axis and its upper corners on the parabola y 5x What are the dimensions of such a rectangle with the greatest possible area Width 2 5 Height 5

Calculus
Limits & ContinuityDetermine whether the sequence converges or diverges If it converges find the limit If the sequence diverges enter DIVERGES 9n 20 lim an 11 an

Calculus
Application of derivativesUse the Fundamental Theorem to evaluate the definite integral exactly 8 x x dx

Calculus
Definite IntegralsA particle is released as part of an experiment Its speed t seconds after release is given by v t 0 6t 12t where v t is in meters per second a How far does the particle travel during the first 6 sec b How far does it travel during the second 6 sec

Calculus
Differential equations1 3 2 A baseball diamond is a square with sides of 90 feet To the nearest foot how long is a throw to first base from third base the child to reach the water 3 A soccer ball is kicked from the ground and its height in meters above ground is modeled by the function 4 9t 19 6t where t represents the time in seconds after the ball is kicked How long is the ball in 0 4 9 19 6t e air 04 9t
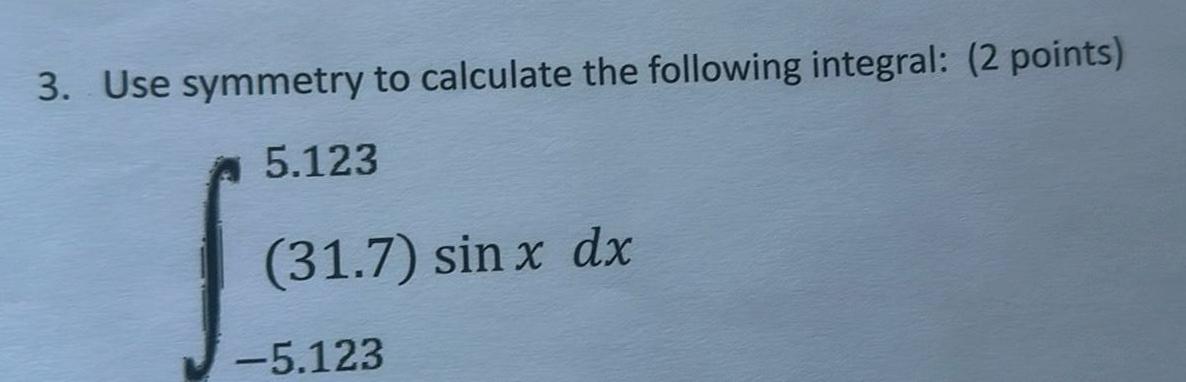
Calculus
Definite Integrals3 Use symmetry to calculate the following integral 2 points 5 123 31 7 sin x dx 5 123
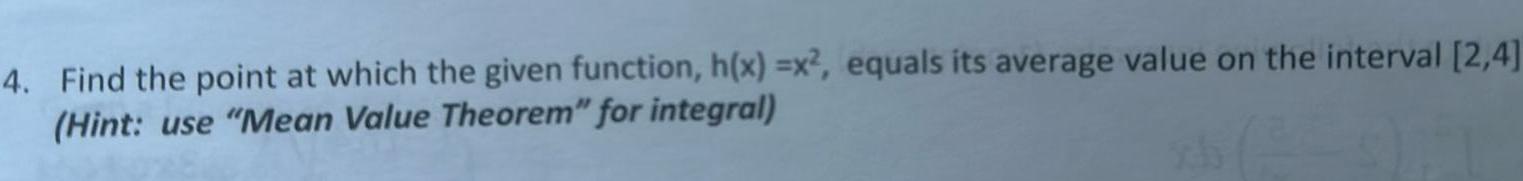
Calculus
Application of derivatives4 Find the point at which the given function h x x2 equals its average value on the interval 2 4 Hint use Mean Value Theorem for integral
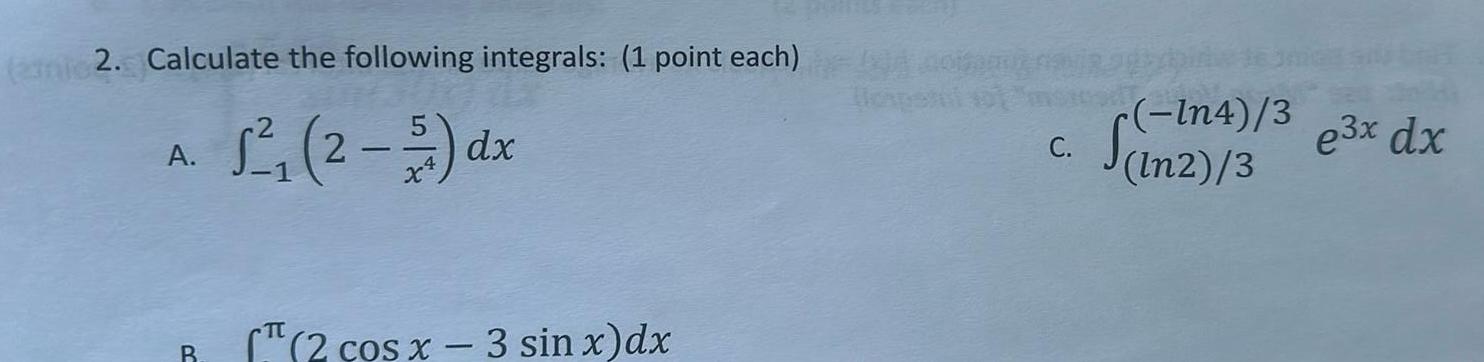
Calculus
Definite Integrals2 Calculate the following integrals 1 point each 2 2 dx A B TT 2 cos x 3 sin x dx Hospel sol In4 3 c S 172743 3 e x dx C ln2 3
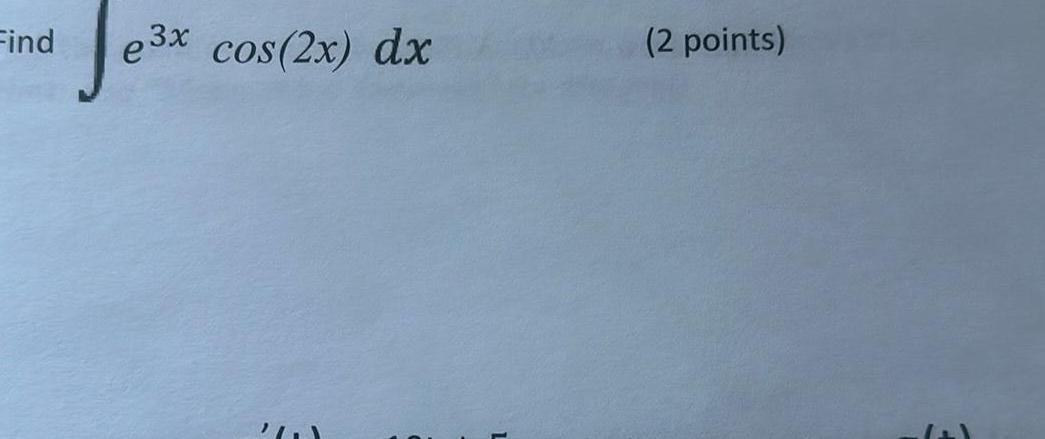
Calculus
Definite Integrals1 Given a function of g x on 1 8 and k x 0 on 1 3 k x dx 10 k x 0 on 3 6 k x dx k x 0 on 6 8 k x dx 5 estimate the following integrals 1 point each c f k x dx A k x dx d Are B Sk x dx D fg k x dx

Calculus
Indefinite Integration5 Use the Variations on the Substitution Method to calculate the following integral 2 points 3x 4 hint set u S x sin 3x 4 dx

Calculus
Definite IntegralsA 0 60 sin 30x dx 2 points each hint set u 30x Table 4 9 Ti for Quiz 4 21 points 2tniog St 5 bine 2 mt 1 B f 3x lnx dxist hint use integration by parts set x and dy

Calculus
Application of derivatives1 2 1 point You hold two sheets paper vertically facing each other You blow air between the sheets and observe that they are moving closer toward each other Which statement is correct As you blow the air it moves and it causes the pressure between the sheets the increase above the ambient atmospheric pressure As you blow the air between the sheets its movement causes the pressure between the sheets to drop As you blow the air between the sheets its movement creates vacuum between the sheets As you blow the air between the sheets it displaces all the air between the sheets and they collapse 1 point In a section of horizontal pipe with a diameter of 50 cm the velocity of the water flowing is 4 0 m s and the pressure is 4 3 kPa What volume of water flows per unit time in the pipe Give your answer in m 3 s but do not include the units in the answer box Type your answer

Calculus
Limits & Continuity8 Consider the function f x 3x 5x 4 7x a Find a term that when added to f would change the end behavior of f as but not as x b Find a term that when added to f would change the end behavior of f on both sides as x and as c Find a term that when added to f would NOT change the end behavior of f
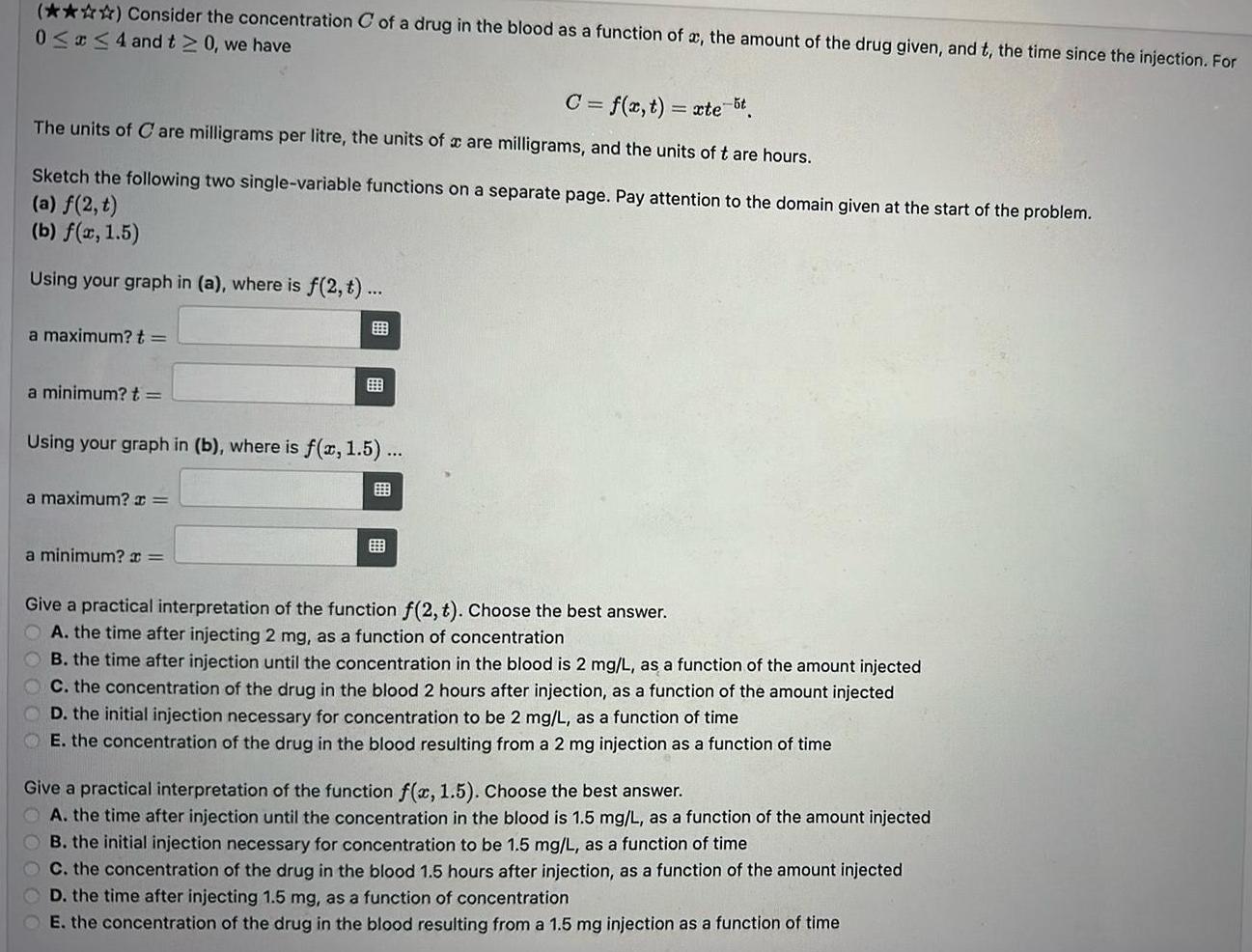
Calculus
Application of derivativesConsider the concentration C of a drug in the blood as a function of a the amount of the drug given and t the time since the injection For 0 x 4 and t 0 we have C f x t xte t The units of Care milligrams per litre the units of a are milligrams and the units of t are hours Sketch the following two single variable functions on a separate page Pay attention to the domain given at the start of the problem a f 2 t b f x 1 5 Using your graph in a where is f 2 t a maximum t a minimum t Using your graph in b where is f x 1 5 a maximum x a minimum x Give a practical interpretation of the function f 2 t Choose the best answer A the time after injecting 2 mg as a function of concentration B the time after injection until the concentration in the blood is 2 mg L as a function of the amount injected C the concentration of the drug in the blood 2 hours after injection as a function of the amount injected D the initial injection necessary for concentration to be 2 mg L as a function of time E the concentration of the drug in the blood resulting from a 2 mg injection as a function of time Give a practical interpretation of the function f x 1 5 Choose the best answer A the time after injection until the concentration in the blood is 1 5 mg L as a function of the amount injected OB the initial injection necessary tration to be 1 5 mg L as a function of time C the concentration of the drug in the blood 1 5 hours after injection as a function of the amount injected D the time after injecting 1 5 mg as a function of concentration E the concentration of the drug in the blood resulting from a 1 5 mg injection as a function of time
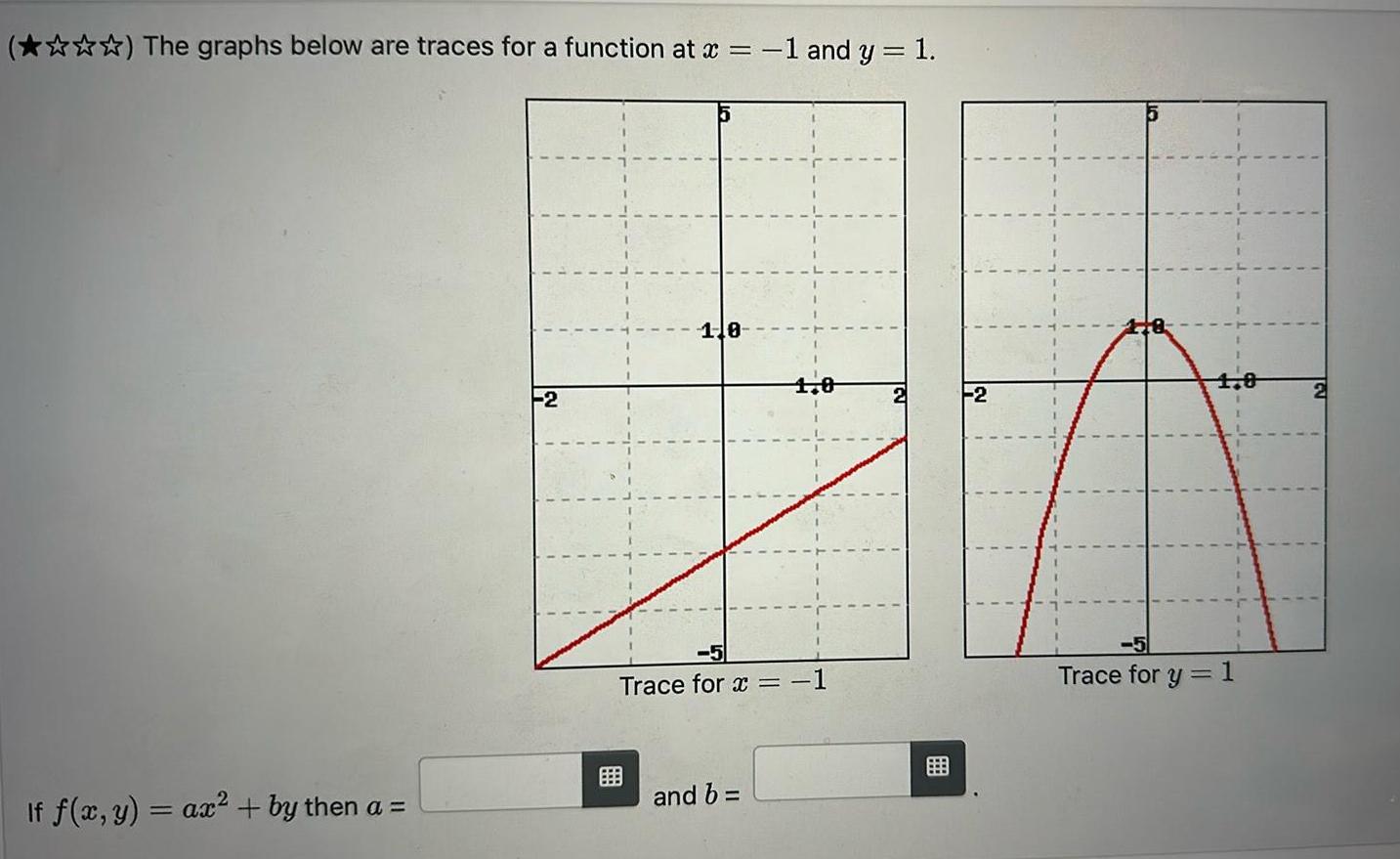
Calculus
Vector CalculusThe graphs below are traces for a function at x If f x y ax by then a 2 110 1 and y 1 and b 1 0 Trace for x 1 2 2 1 0 Trace for y 1 2
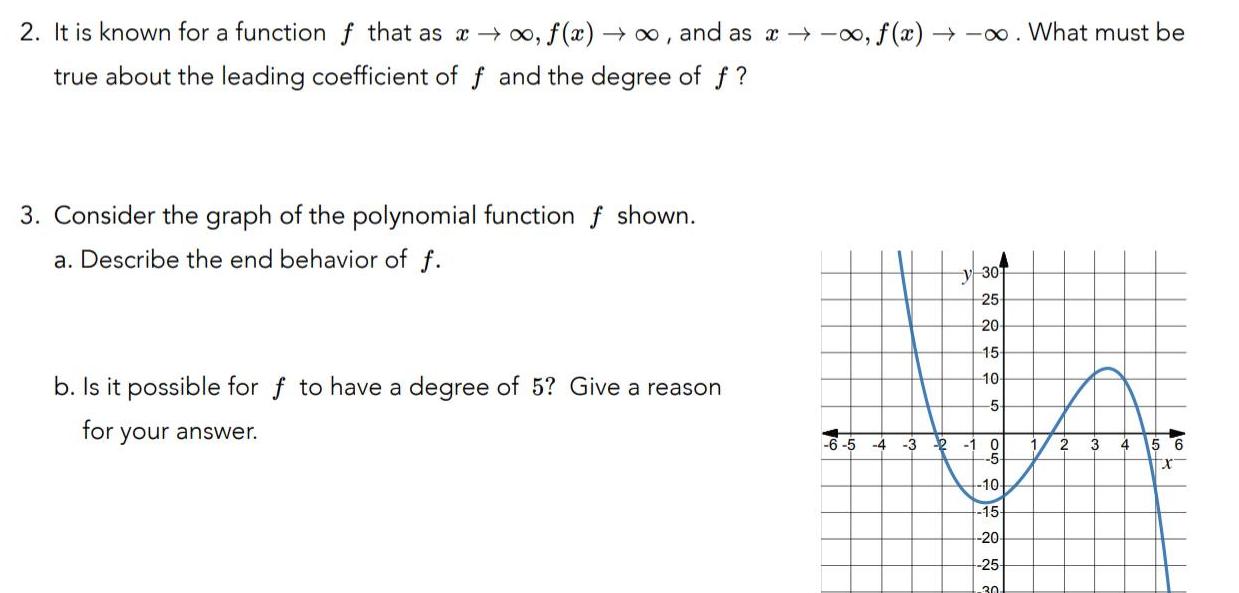
Calculus
Limits & Continuity2 It is known for a function f that as f x and as a o f x What must be true about the leading coefficient of f and the degree of f 3 Consider the graph of the polynomial function f shown a Describe the end behavior of f b Is it possible for f to have a degree of 5 Give a reason for your answer y 30 25 20 15 10 5 3 2 1 6 Go 0 10 15 20 25 30 2 3 4 5 6 X

Calculus
Application of derivativesThe marginal price for a weekly demand of x bottles of shampoo in a drugstore is given by the function shown below Find the price demand equation if the weekly demand is 150 when the price of a bottle of shampoo is 8 What is the weekly demand when the price is 6 50 p x 9 000 3x 50 Find the price demand equation Type an equation www

Calculus
Definite IntegralsAn automobile company is ready to introduce a new line of cars through a national sales campaign After test marketing the line in a carefully selected city the marketing research department estimates that the sales in millions of dollars will increase at the monthly rate of the following function for t months after the campaign has started S t 22 13e 0 1t Ost 24 A What will be the total sales S t t months after the beginning of the national sales campaign if we assume no sales at the beginning of the campaign s t
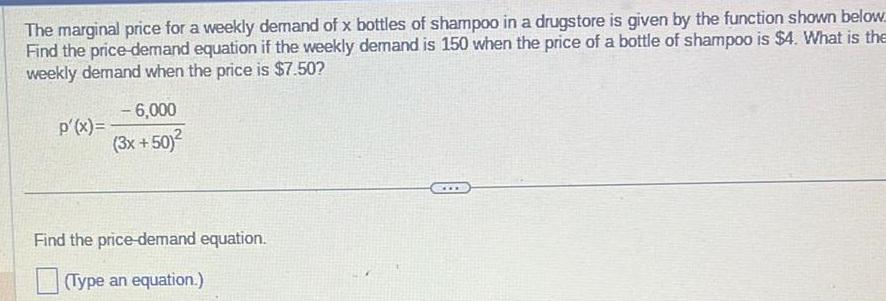
Calculus
Definite IntegralsThe marginal price for a weekly demand of x bottles of shampoo in a drugstore is given by the function shown below Find the price demand equation if the weekly demand is 150 when the price of a bottle of shampoo is 4 What is the weekly demand when the price is 7 50 p x 6 000 3x 50 Find the price demand equation Type an equation

Calculus
Application of derivativesA yeast culture is growing at the rate of W t 0 40 1 grams per hour If the starting culture weighs 4 grams what wi be the weight of the culture W t after t hours After 9 hours The weight of the culture after t hours will be W t

Calculus
Vector CalculusFind the solution of the exponential equation as in Example 1 Enter your answers as a comma separated list 22x3 1 X

Calculus
Definite IntegralsA one meter long bar is heated unevenly with temperature in C at a distance x meters from one end at time t given by H x t 120e 0 15t sin x 0 x 1 On a sheet of paper sketch a graph of H against for t 0 and t 1 Think about why your graphs make sense a Calculate each of H 0 2 t H 0 8 t Be sure that you can say in words what the practical interpretation in terms of temperature of these two partial derivatives is and why each has the sign that it does b Calculate x t Again be sure that you understand why it has the sign that it does and what its interpretation in terms of temperature is

Calculus
Vector CalculusFind the solution of the exponential equation as in Example 1 Enter your answers as a comma separated list e 3x e4x 3 X
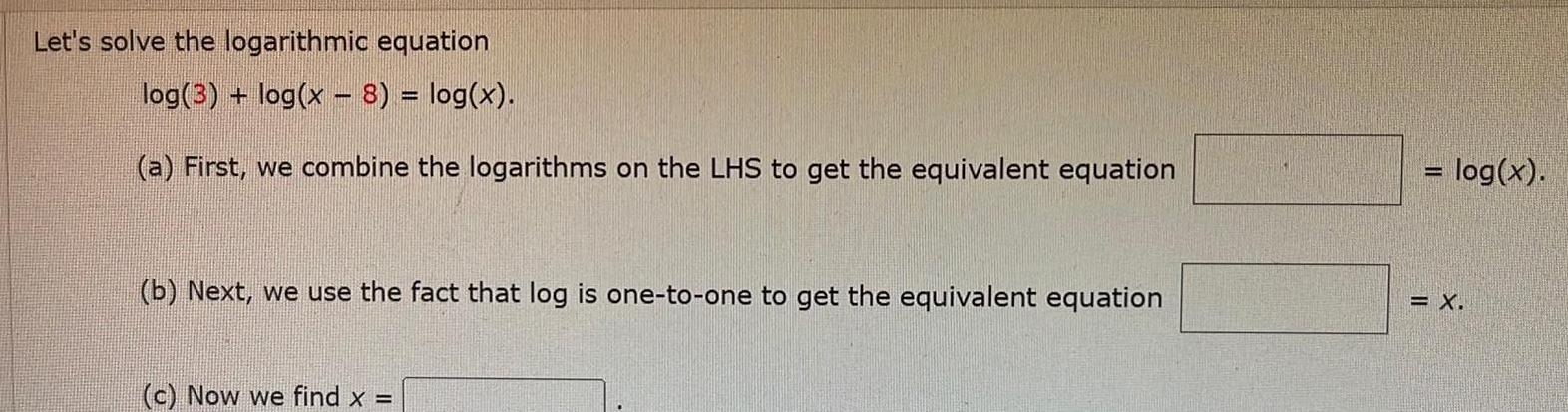
Calculus
Application of derivativesLet s solve the logarithmic equation log 3 log x 8 log x a First we combine the logarithms on the LHS to get the equivalent equation b Next we use the fact that log is one to one to get the equivalent equation c Now we find x log x X
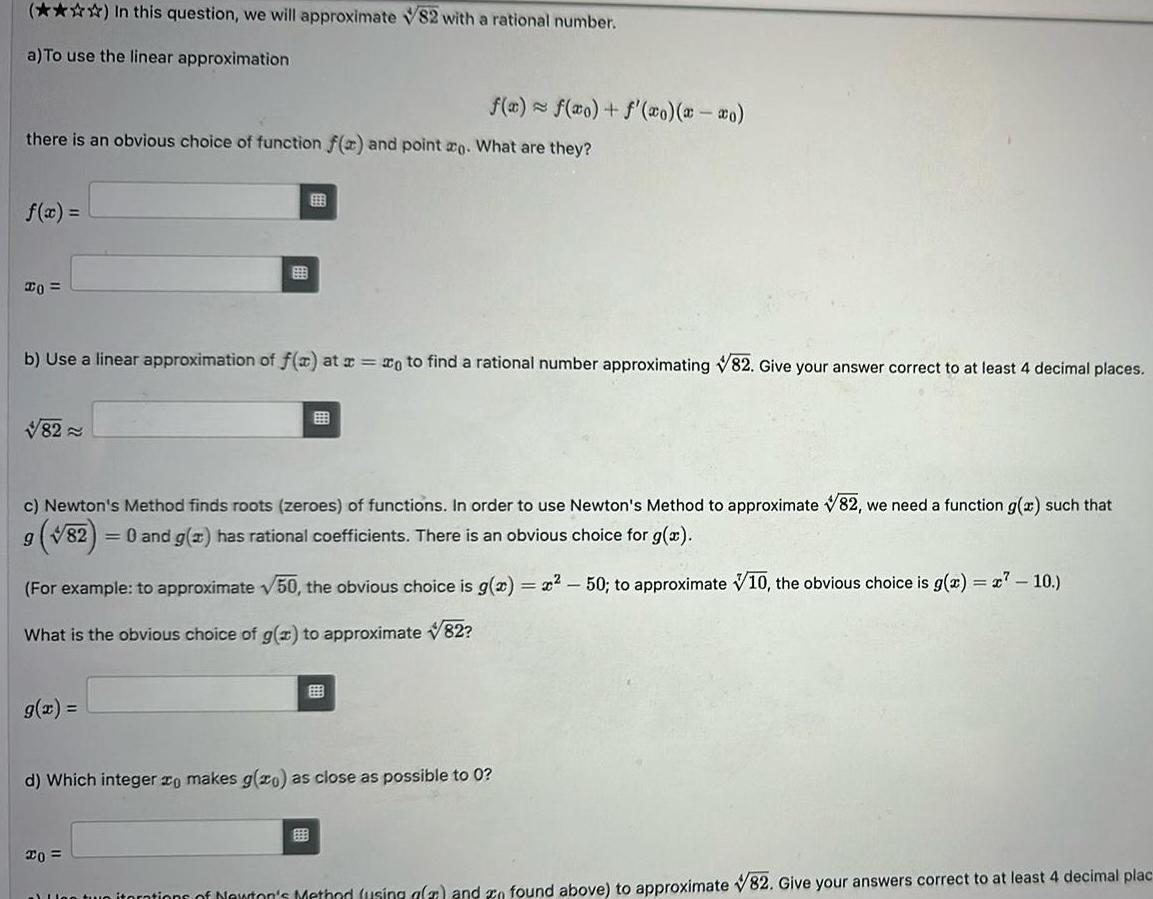
Calculus
Application of derivativesIn this question we will approximate 82 with a rational number a To use the linear approximation there is an obvious choice of function f x and point ao What are they f x 20 82 f x f x f xo x xo 999 b Use a linear approximation of f x at x xo to find a rational number approximating 82 Give your answer correct to at least 4 decimal places c Newton s Method finds roots zeroes of functions In order to use Newton s Method to approximate 82 we need a function g x such that 9 82 0 and g x has rational coefficients There is an obvious choice for g x For example to approximate 50 the obvious choice is g x x 50 to approximate 10 the obvious choice is g x x7 10 What is the obvious choice of g x to approximate 82 20 d Which integer zo makes g zo as close as possible to 0 on two iterations of Newton s Method using afa and n found above to approximate 82 Give your answers correct to at least 4 decimal plac

Calculus
DifferentiationLet z x 4y Then The rate of change in zat 3 1 as we change x but hold y fixed is The rate of change in zat 3 1 as we change y but hold a fixed is

Calculus
Application of derivativesThe question asks us to sketch the function y cos 3t First note that the function is a cosine function and will have that basic shape From the text the general form of a non shifted cosine function is y a cos bt The text also tells us that a is the amplitude that is the maximum height above zero that the function attains Note that the amplitude must be a positive number Looking at our function the amplitude is
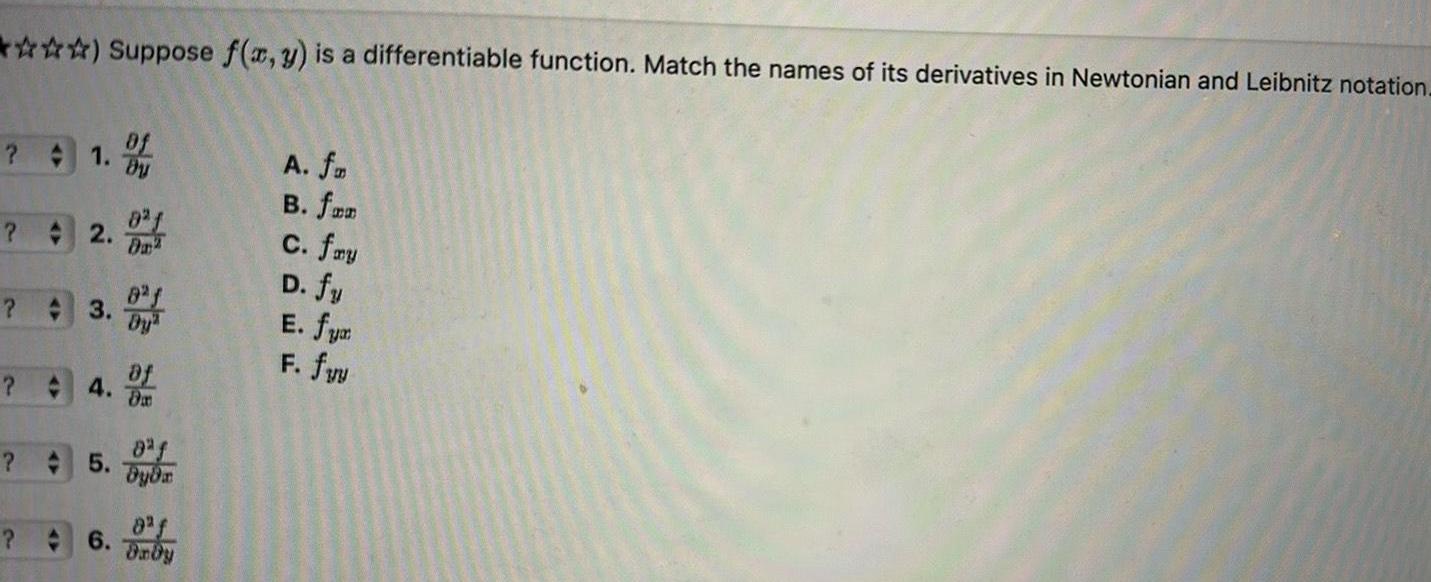
Calculus
Application of derivativesSuppose f x y is a differentiable function Match the names of its derivatives in Newtonian and Leibnitz notation 1 2 3 4 5 of By of Da dyda 6 Drby A fm B fan c fry D fy E fym F fu
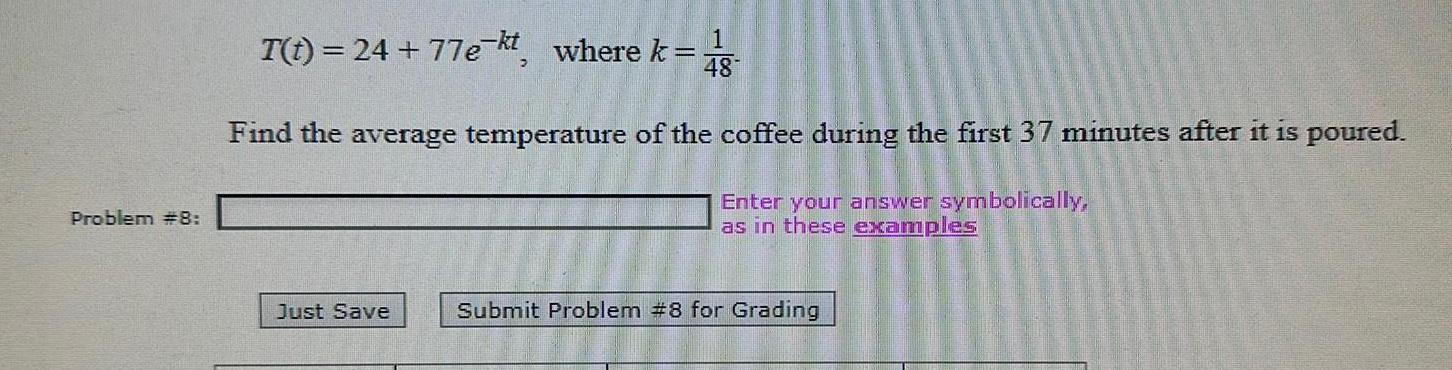
Calculus
Application of derivativesProblem 8 I t 24 77e kt where k 48 Find the average temperature of the coffee during the first 37 minutes after it is poured Enter your answer symbolically as in these examples Just Save Submit Problem 8 for Grading
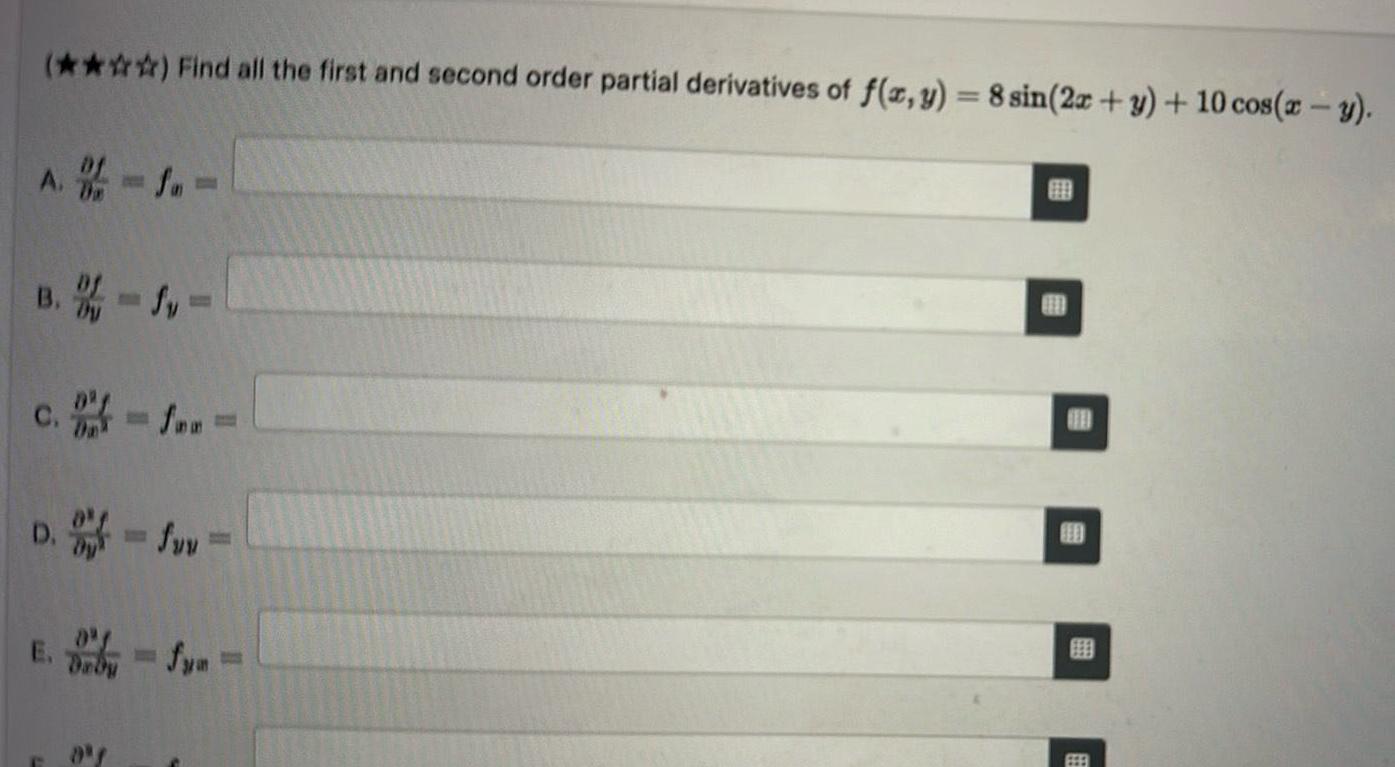
Calculus
DifferentiationFind all the first and second order partial derivatives of f x y 8 sin 2x y 10 cos x y A 1 B Sv c fen D ffwr 0 f FEEL

Calculus
Application of derivativesFind the partial derivatives of the function fx x y fy x y fay x y f ra f x y xye B
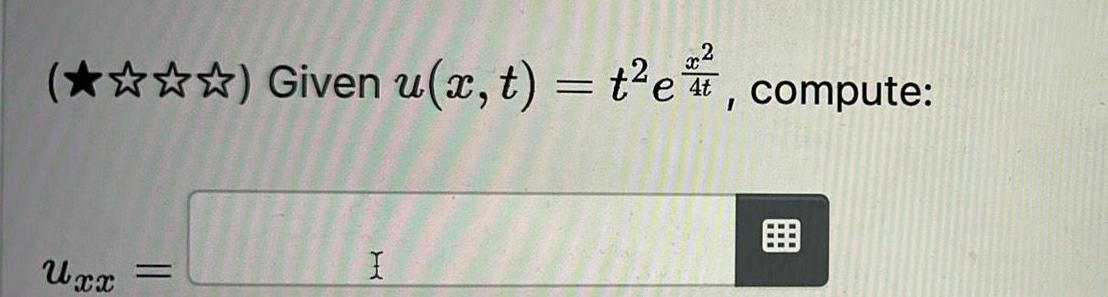
Calculus
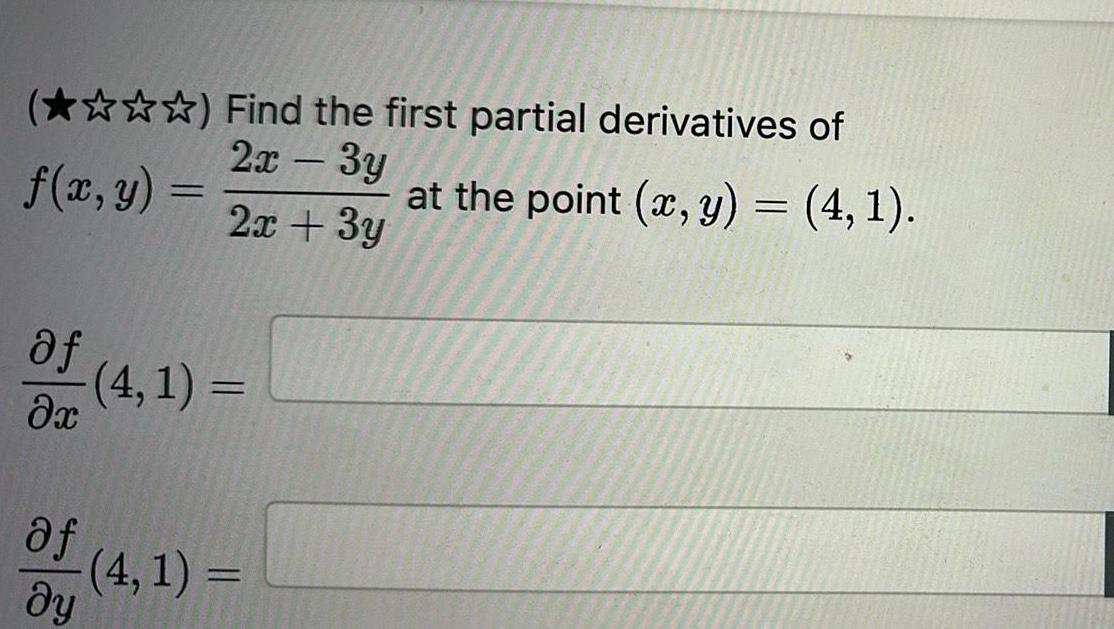
Application of derivativesFind the first partial derivatives of 2x 3y 2x 3y f x y af x af 4 1 4 1 dy at the point x y 4 1
Calculus
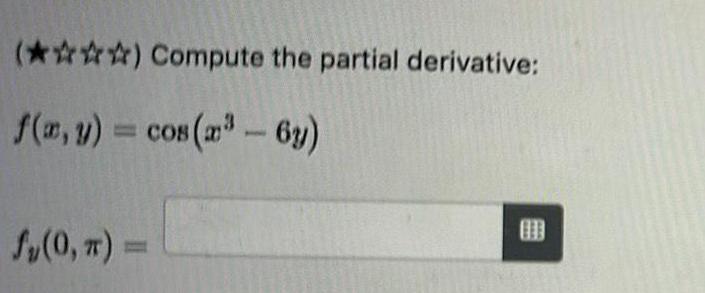
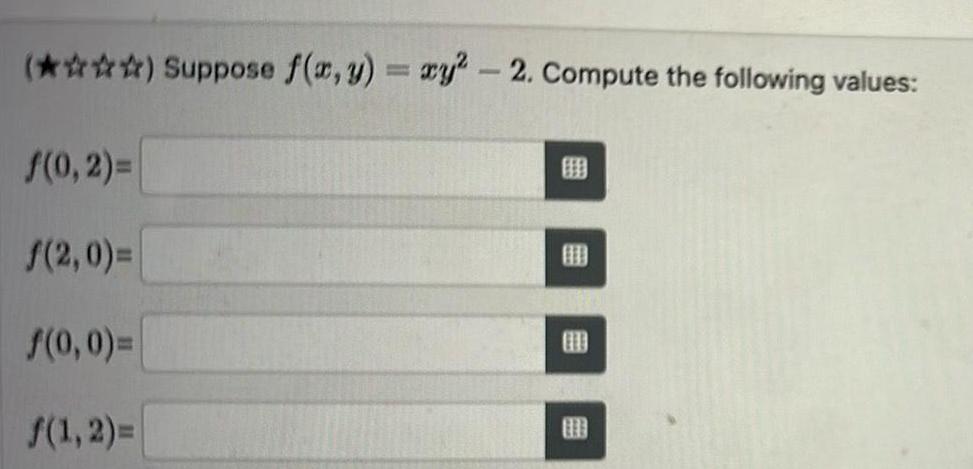
Application of derivativesSuppose f x y xy 2 Compute the following values f 0 2 2 0 f 0 0 1 2

Calculus
Limits & Continuityroblem 6 Find an integral which represents the volume of the solid obtained by rotating the region enclosed by the curves y x and y 8x about the line x 8 Problem 6 64 A 50 D G A 8 8 dy B 50 7 z 8 8 5 C a 8 2 8 2 dy 64 64 a 8 2 8 y 8 5 8 2 8 8 dv 64 Just Save Problem 6 Your Answer 8 E a 8 8 5 f r 8 8 5 8 dy F dy Submit Problem 6 for Grading Attempt 1 Attempt 2 Attempt 3 G A 4