Application of derivatives Questions and Answers

Calculus
Application of derivatives4 f n 2 cos x 2n n T 1 Find the intervals on which f n is increacing and decreasing 2 Identify the local maximum and minimum of f k 3 Identify the intervals on which f x is concave up and concove down 4 Identify the inflection points
Calculus
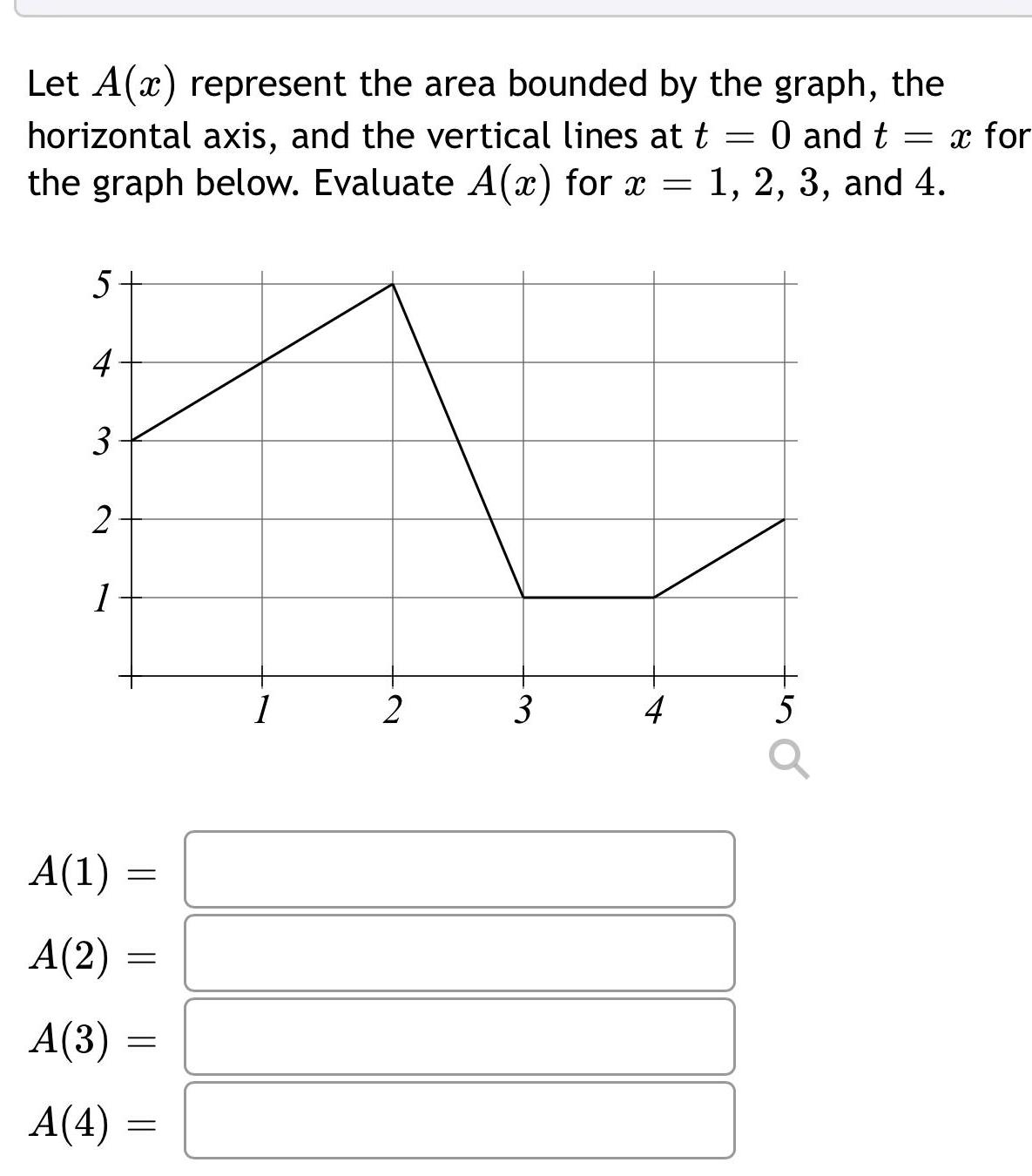
Application of derivativesLet A x represent the area bounded by the graph the 0 and t x for horizontal axis and the vertical lines at t the graph below Evaluate A x for x 1 2 3 and 4 5 4 3 2 1 A 1 A 2 A 3 A 4 1 2 3 4 5 a
Calculus
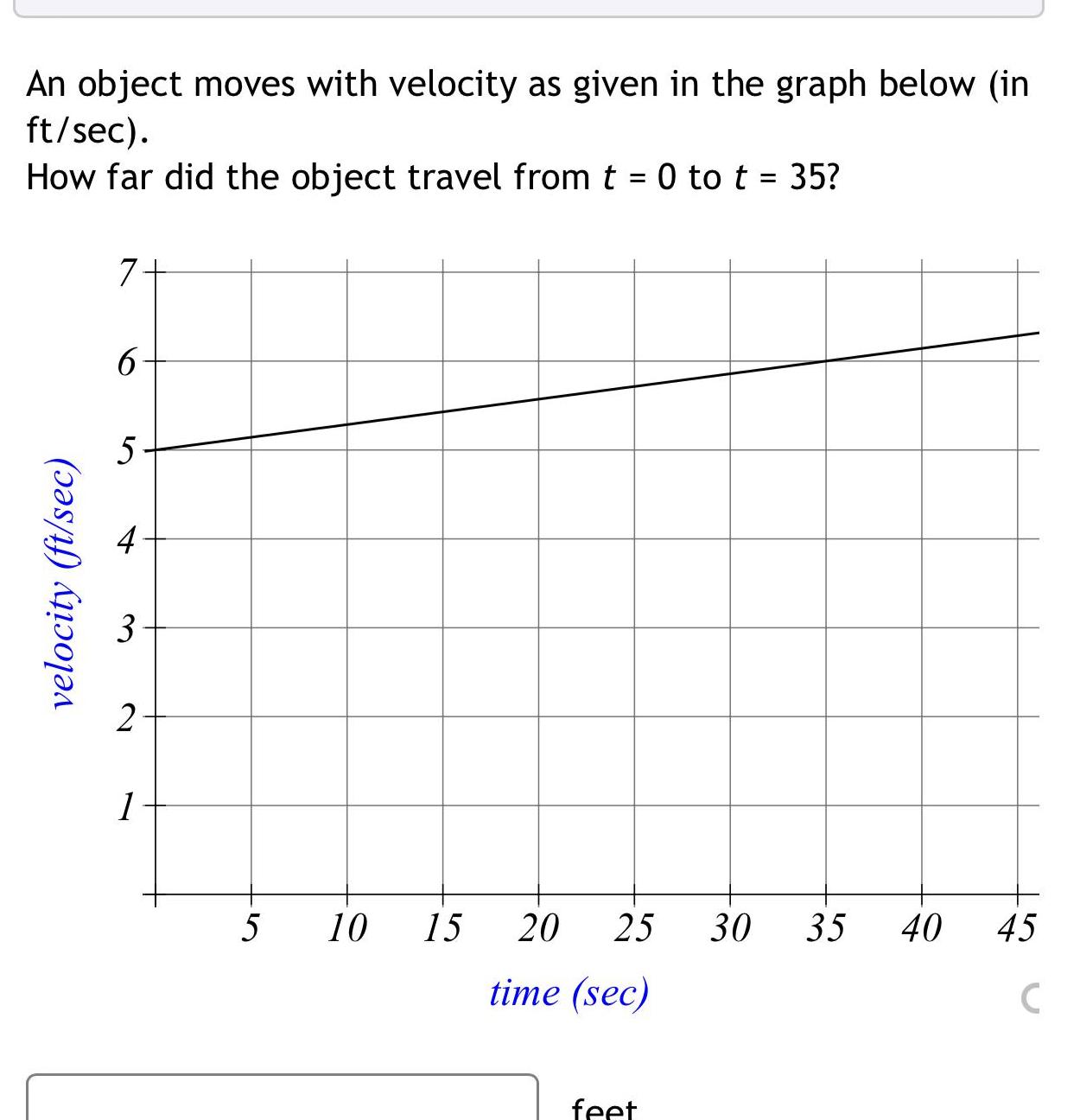
Application of derivativesAn object moves with velocity as given in the graph below in ft sec How far did the object travel from t 0 to t 35 velocity ft sec 7 6 5 2 1 5 10 15 20 25 30 35 time sec feet 40 45 C
Calculus
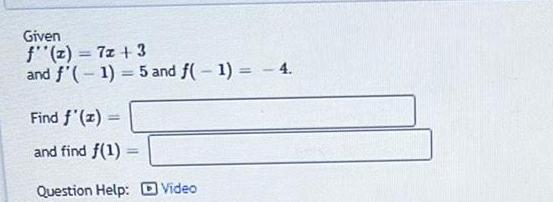
Application of derivativesGiven f z 7x 3 and f 1 5 and f 1 4 Find f x and find f 1 Question Help Video

Calculus
Application of derivativesis the headquarters of Greedy The cable company is about to expand service to two nearby towns Springfield and Shelbyville There needs to be cable connecting Centerville to both towns The idea is to save on the cost of cable by arranging the cable in a Y shaped configuation Centerville is located at 7 0 in the xy plane Springfield is at 0 2 and Shelbyville is at 0 2 The cable runs from Centerville to some point x 0 on the x axis where it splits into two branches going to Springfield and Shelbyville Find the location x 0 that will minimize the amount of cable between the 3 towns and compute the amount of cable needed Justify your answer To solve this problem we need to minimize the following function of x f x We find that f x has a critical number at x To verify that f x has a minimum at this critical number we compute the second derivative f x and find that its value at the critical number is positive number Thus the minimum length of cable needed is 2 a
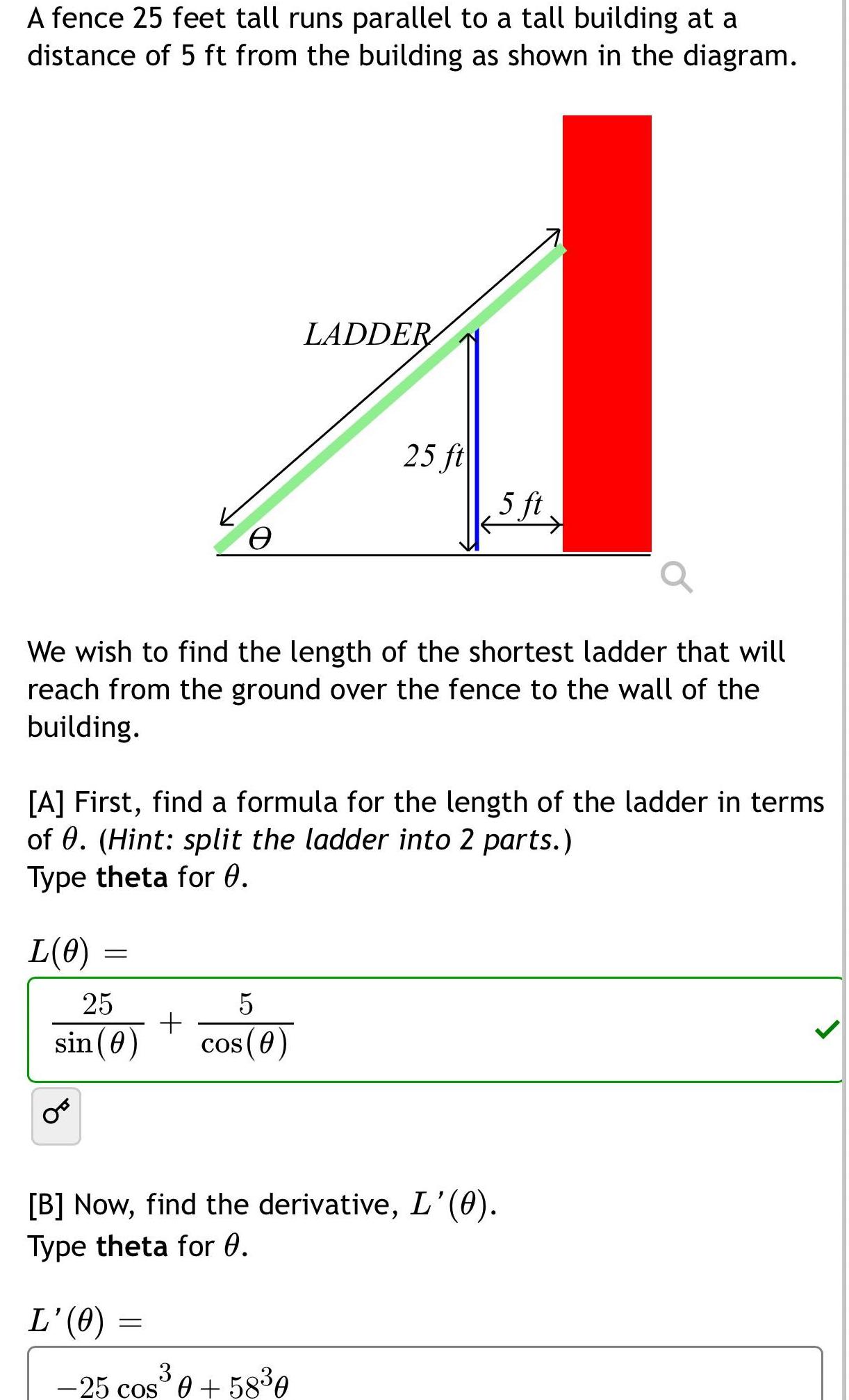
Calculus
Application of derivativesA fence 25 feet tall runs parallel to a tall building at a distance of 5 ft from the building as shown in the diagram L 0 We wish to find the length of the shortest ladder that will reach from the ground over the fence to the wall of the building 25 sin 0 e A First find a formula for the length of the ladder in terms of 0 Hint split the ladder into 2 parts Type theta for 0 L 0 LADDER 5 cos 0 25 ft B Now find the derivative L 0 Type theta for 0 3 25 cos 0 58 0 5 ft

Calculus
Application of derivativesA microwaveable cup of soup package needs to be constructed in the shape of cylinder to hold 300 cubic centimeters of soup The sides and bottom of the container will be made of styrofoam costing 0 03 cents per square centimeter The top will be made of glued paper costing 0 07 cents per square centimeter Find the dimensions for the package that will minimize production cost Helpful information h height of cylinder r radius of cylinder Volume of a cylinder V tr h Area of the sides A 2 rh Area of the top bottom A r To minimize the cost of the package Radius Height Minimum cost cm cm cents

Calculus
Application of derivativesnce 25 all par to a call ing at a distance of 5 ft from the building as shown in the diagram L 0 e LADDER We wish to find the length of the shortest ladder that will reach from the ground over the fence to the wall of the building 25 ft A First find a formula for the length of the ladder in terms of 0 Hint split the ladder into 2 parts Type theta for 0 5 ft B Now find the derivative L 0 Type theta for 0 L 0 C Once you find the value of that makes L 0 0 substitute that into your original function to find the length

Calculus
Application of derivativesc Find the values of p ER for which the series is convergent 1 n ln n ln In n P n 3 Hint You may use the result about p integral provided that you state d Find the radius of convergence and interval of convergence of the series 2n 272 x 2 n

Calculus
Application of derivatives7 Find a symbolic representation formula for a function f that calculates the gallons of wate in a whirlpool bath after x hours past noon f00150x100 8 Use your function to calculate how many gallons of water are in the bath at 5 00pm Plot and label this point on the graph 160 880 750t 9 Find the difference quotient for f from number 7 f x h f x h 1

Calculus
Application of derivativesTextbook Videos If 2300 square centimeters of material is available to make a box with a square base and an open top find the largest possible volume of the box Volume

Calculus
Application of derivativesf x x 3 Which information is true about f x elect one Of x is neither even nor odd Of x is odd Of x is even O We need more information to determine if f x is even or odd
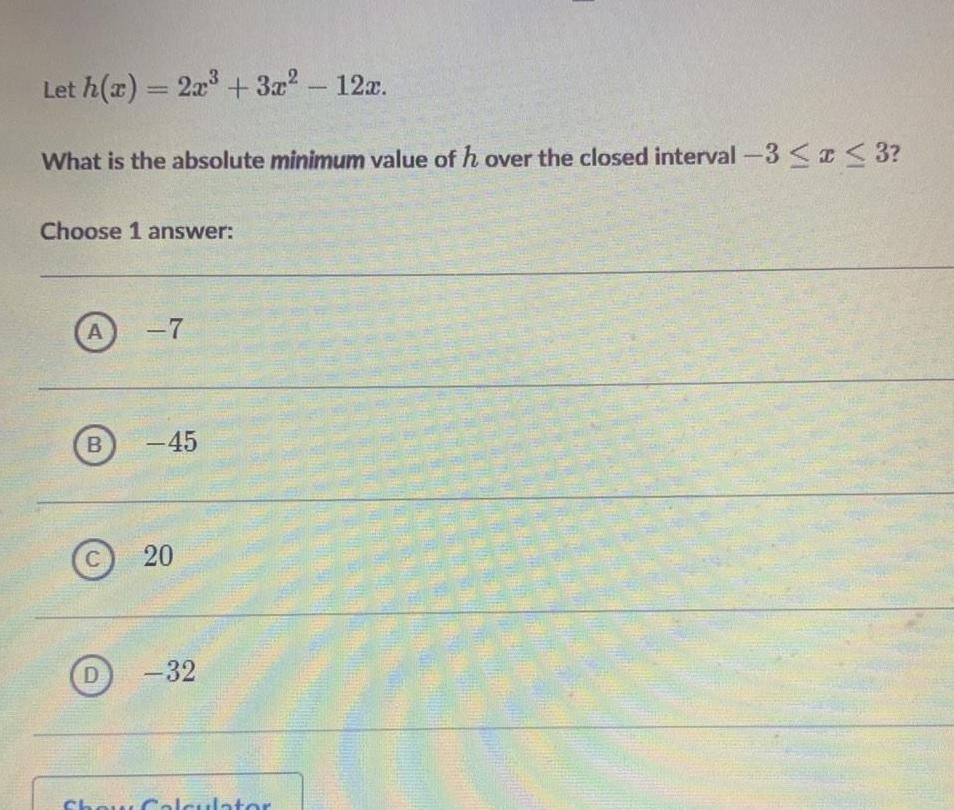
Calculus
Application of derivativesLet h x 2x 3x 12x What is the absolute minimum value of h over the closed interval 3 x 3 Choose 1 answer A B C D 7 45 20 32 Show Calculator TEMAL MFD 79709 ALUMER Mement Par De M EXTERNET of WA
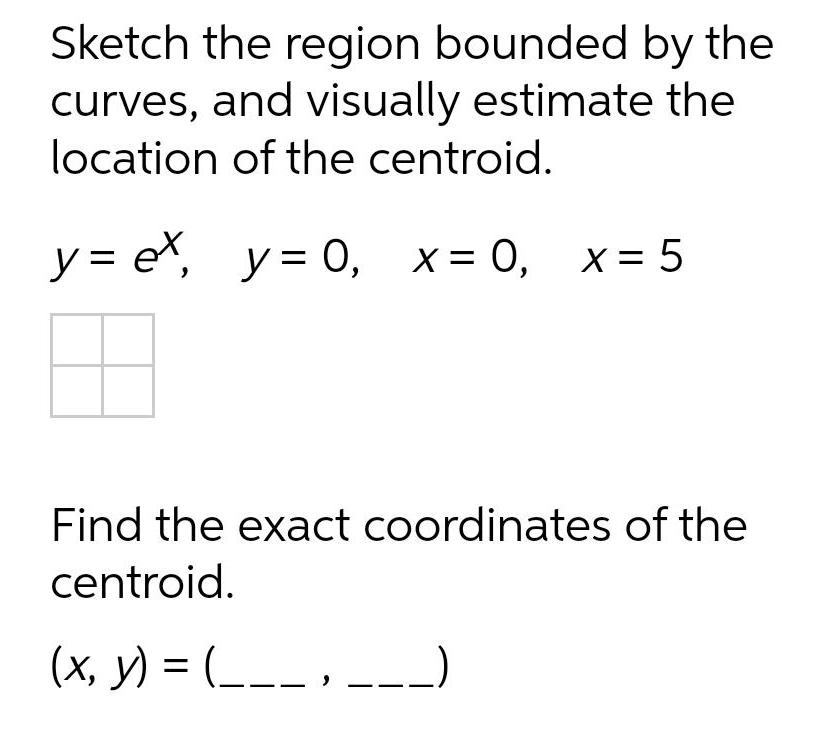
Calculus
Application of derivativesSketch the region bounded by the curves and visually estimate the location of the centroid y ex y 0 x 0 x 5 Find the exact coordinates of the centroid x y

Calculus
Application of derivativesA circle is inside a square The radius of the circle is increasing at a rate of 1 meter per day and the sides of the square are decreasing at a rate of 1 meter per day When the radius is 6 meters and the sides are 16 meters then how fast is the AREA outside the circle but inside the square changing The rate of change of the area onclosed botwoon the circle
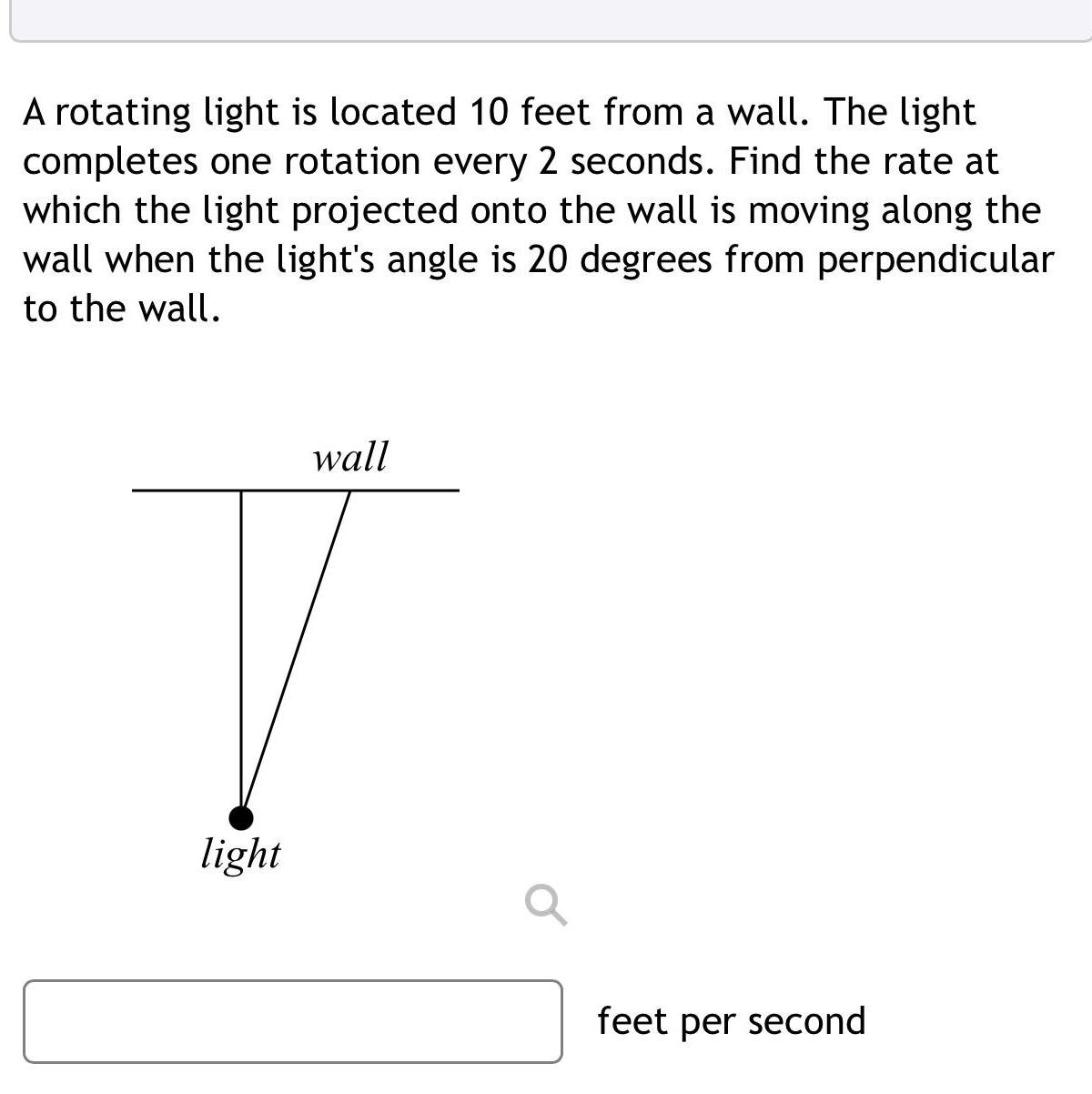
Calculus
Application of derivativesA rotating light is located 10 feet from a wall The light completes one rotation every 2 seconds Find the rate at which the light projected onto the wall is moving along the wall when the light s angle is 20 degrees from perpendicular to the wall light wall feet per second

Calculus
Application of derivativesGravel is being dumped from a conveyor belt at a rate of 40 cubic feet per minute It forms a pile in the shape of a right circular cone whose base diameter and height are always equal How fast is the height of the pile increasing when the pile is 19 feet high Recall that the volume of a right circular cone with height h and radius of the baser is given by 1 V r h ft

Calculus
Application of derivativesThe altitude of a triangle is increasing at a rate of 2 5 centimeters minute while the area of the triangle is increasing at a rate of 2 5 square centimeters minute At what rate is the base of the triangle changing when the altitude is 8 5 centimeters and the area is 90 square centimeters 156 16 x cm min
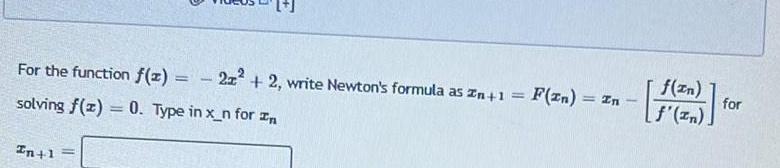
Calculus
Application of derivativesFor the function f x solving f x 0 Type in x n for In In 1 2z 2 write Newton s formula as n 1 F In In f zn f zn for
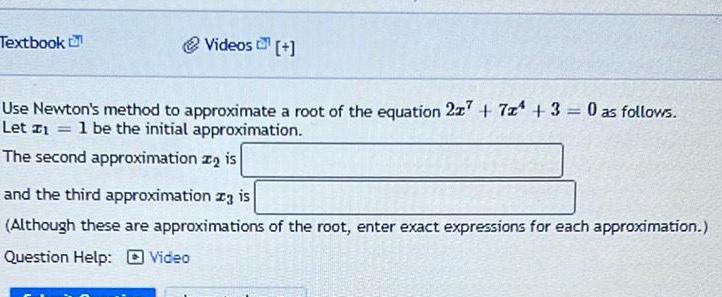
Calculus
Application of derivativesTextbook Videos Use Newton s method to approximate a root of the equation 227 7 3 0 as follows Let z 1 be the initial approximation The second approximation is and the third approximation za is Although these are approximations of the root enter exact expressions for each approximation Question Help Video

Calculus
Application of derivativesA company is forecasted to generate free cash flows of 30 million next year and 40 million the year t 2 After that cash flows are projected to grow at a 2 annual rate in perpetuity The company s cost of capital is 8 What s it enterprise value today Answer in millions rounded to a whole number e g 246 3 million 246

Calculus
Application of derivativesDepending on the demand for his babysitting services Trent makes 17 to 59 babysitting each week If he writes down the amount of money he makes weekly what kind of sequence will he see

Calculus
Application of derivativesThe radius of a sphere is decreasing at a constant rate of 2 meters per minute At the instant when the radius of the sphere is 7 meters what is the rate of change of the volume The volume of a sphere can be found with the equation V r Round your answer to three decimal places

Calculus
Application of derivativesThe radius of a sphere is increasing at a rate of 7 5 meters per minute At a certain instant the radius is 5 meters What is the rate of change of the surface area of the sphere at that instant in square meters per minute
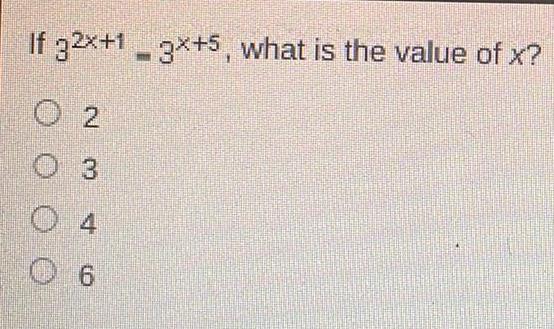

Calculus
Application of derivativesRelated Rates One Formula Jan 05 5 50 20 PM The height of a cylinder is increasing at a constant rate of 2 meters per second and the volume is decreasing at a rate of 800 cubic meters per second At the instant when the radius of the cylinder is 5 meters and the volume is 648 cubic meters what is the rate of change of the radius The volume of a cylinder can be found with the equation V Tr h Round your answer to three decimal places
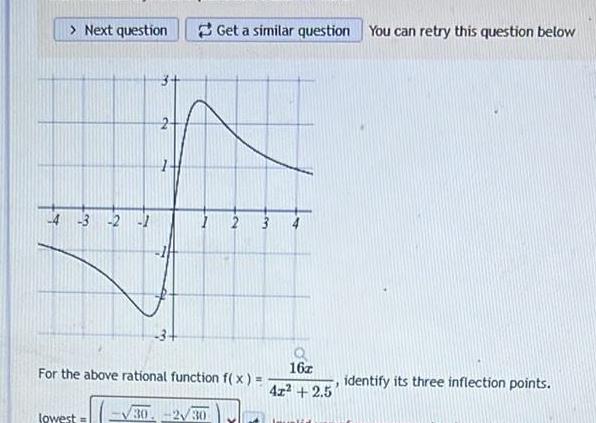
Calculus
Application of derivativesNext question 1 3 2 1 lowest Get a similar question You can retry this question below For the above rational function f x 30 230 2 16z 42 2 5 identify its three inflection points
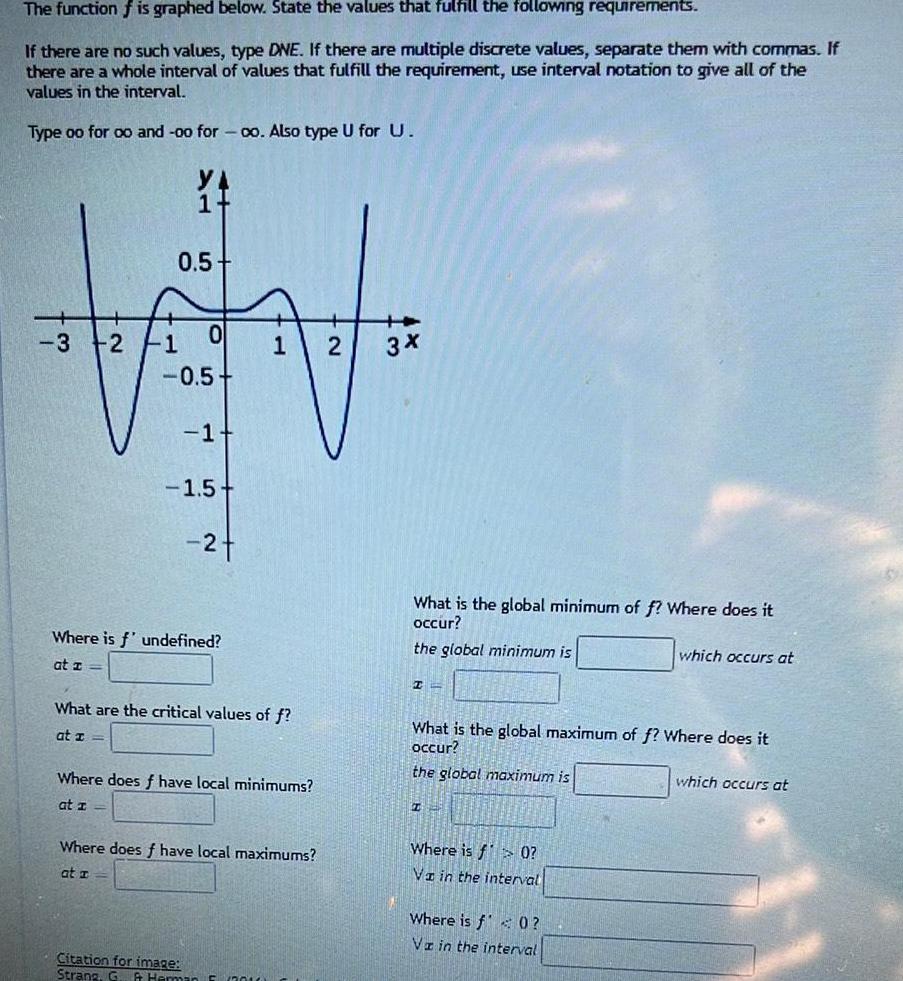
Calculus
Application of derivativesThe function f is graphed below State the values that fulfill the following requirements If there are no such values type DNE If there are multiple discrete values separate them with commas If there are a whole interval of values that fulfill the requirement use interval notation to give all of the values in the interval Type oo for oo and oo for co Also type U for U 3 2 Te CA 0 5 O 0 5 1 1 5 2 Where is f undefined at I 1 What are the critical values of f at I Where does f have local minimums at 1 Citation for image Strang G Herman Where does f have local maximums at I 2 3 3x What is the global minimum of f Where does it occur the global minimum is IL What is the global maximum of f Where does it occur the global maximum is Z Where is f 0 VI in the interval which occurs at Where is f0 VI in the interval which occurs at
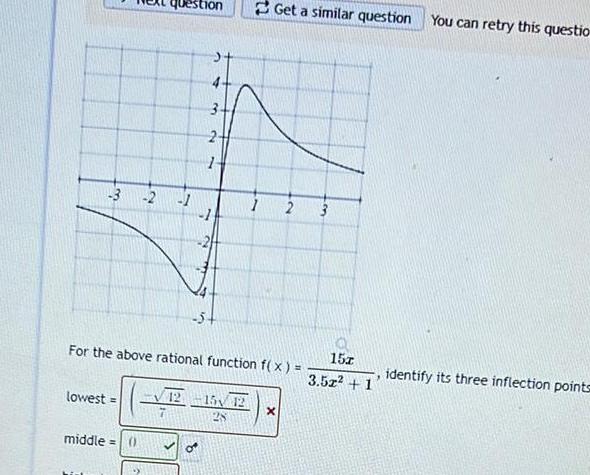
Calculus
Application of derivatives3 2 lowest middle 1 For the above rational function f x 7 Get a similar question You can retry this questio 12 15 12 28 1 2 3 X 15z 3 5z 1 identify its three inflection points
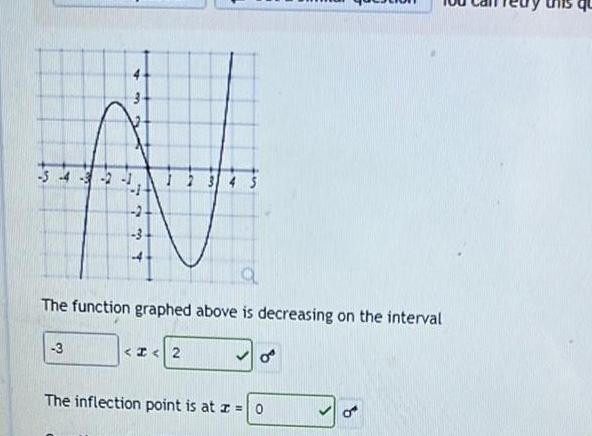
Calculus
Application of derivatives4 2 737 3 1 2 3 4 5 q The function graphed above is decreasing on the interval 2 The inflection point is at z 0 d
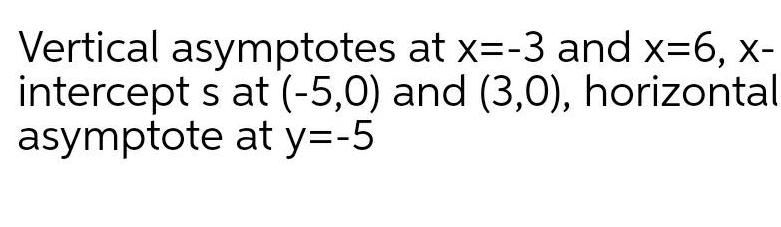
Calculus
Application of derivativesVertical asymptotes at x 3 and x 6 x intercept s at 5 0 and 3 0 horizontal asymptote at y 5
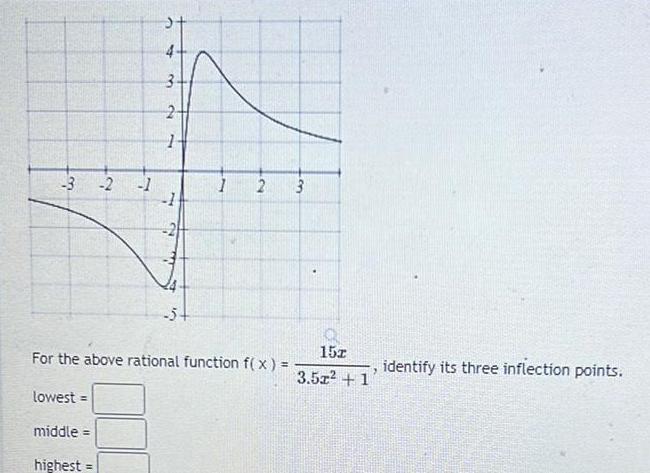
Calculus
Application of derivatives3 2 1 lowest e middle highest my f w 2 1 1 For the above rational function f x 2 3 15z 3 52 1 identify its three inflection points

Calculus
Application of derivativesx a sqrt p b c where a 80 b 22 and c 394 Find the instantaneous rate of change of the supply with respect to price when the price is 74 Round to the nearest hundredth 2 decimal places helmets per dollar
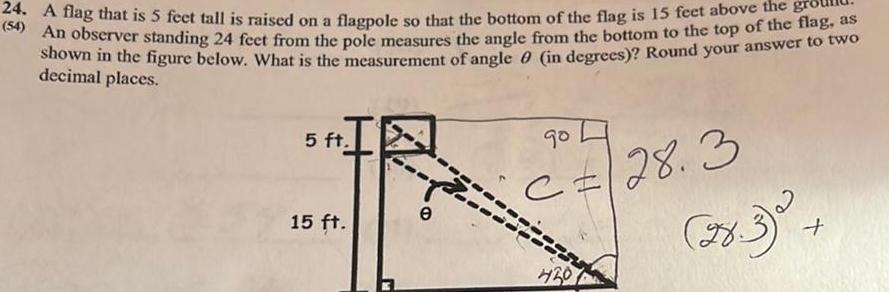
Calculus
Application of derivatives24 A flag that is 5 feet tall is raised on a flagpole so that the bottom of the flag is 15 feet above the 54 An observer standing 24 feet from the pole measures the angle from the bottom to the top of the flag as shown in the figure below What is the measurement of angle 0 in degrees Round your answer to two decimal places 5 ft 15 ft e 90 C 28 3 4201 78 3

Calculus
Application of derivativesL V32 The formula P 2n can be used to approximate the period of a pendulum where L is the pendulum s length in feet and P is the pendulum s period in seconds If a pendulum s period is 1 6 seconds which of the following is closest to the length of the pendulum 4 2 ft 1 4 ft 2 1 ft
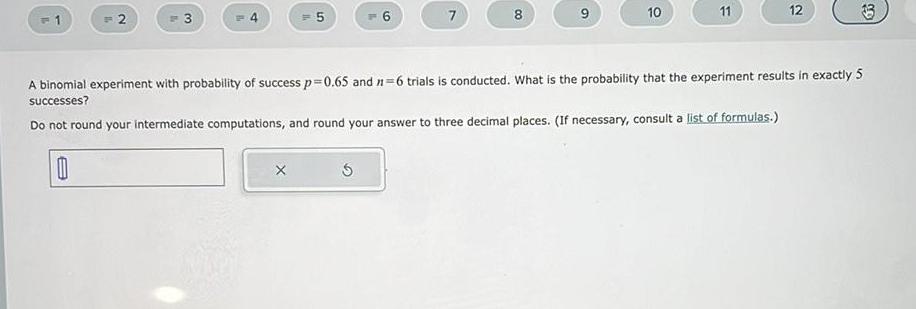
Calculus
Application of derivatives1 2 3 5 X 6 5 7 8 9 10 11 12 A binomial experiment with probability of success p 0 65 and 1 6 trials is conducted What is the probability that the experiment results in exactly 5 successes Do not round your intermediate computations and round your answer to three decimal places If necessary consult a list of formulas 0 33
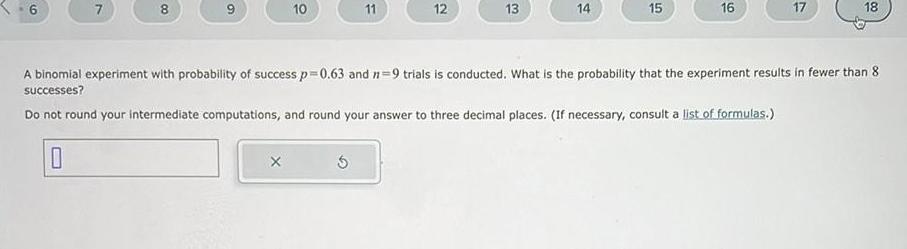
Calculus
Application of derivatives6 7 8 9 10 X 11 12 13 14 15 16 17 18 A binomial experiment with probability of success p 0 63 and 7 9 trials is conducted What is the probability that the experiment results in fewer than 8 successes Do not round your intermediate computations and round your answer to three decimal places If necessary consult a list of formulas 0

Calculus
Application of derivativesflaming stone over a castle wall It is mounted on a Small hill and has a parabolic trajectory neglecting air resistance Once it crashes into the ground on the other side of the castle Wall it comes to rest This motion is described by the function below where X measured in meters represents horizontal displacement from the launch position and y f x represents vertical distance from the ground measured in meters f x 0 25 x 2 3 15 x 5 Detecmine the contextual domain and range and justify your answers What is the peak height of the flaming stone
Calculus
Application of derivatives6 Construct a 99 confidence interval for the population standard deviation o if a sample of size 10 has standard deviation s 12 6 Round the answers to at least two decimal places A 99 confidence interval for the population standard deviation is o S 8 E S d

Calculus
Application of derivativesThe Cauchy Problem for the Diffusion Equation We consider the initial value problem for a one dimensional diffusion equation with no sources or sinks 2 12 23 Ut KUxx x x t 0 where is a diffusivity constant with the initial condition u x 0 f x r 00 2 12 24

Calculus
Application of derivatives2 Find all local extreme values of f x 2x 30 The FIRST local extreme value moving from left to right on the graph is a Select an answer The SECOND extreme value moving from left to right on the graph is a Select an answer at Select an answer minimum maximum at
Calculus
Application of derivativesTextbook Consider the function f z 1 7z on the interval 3 3 Find the average or mean slope of the function on this interval i e f 3 f 3 3 3 By the Mean Value Theorem we know there exists a c in the open interval 3 3 such that f c is equal to this mean slope For this problem there is only one c that works Find it
Calculus
Application of derivativesThe function f x 2x 241 72z 5 has one local minimum and one local maximum Use a graph of the function to estimate these local extrema This function has a local minimum at z and a local maximum at z Question Help Video 1 with output value with output value Video 2 Video 3
Calculus
Application of derivativesTextbook Find the critical numbers of the function f x 121 75x your answers to three decimal places X X X Videos Question Help is a Select an answer is a Select an answer is a Select an answer 100 3 and classify them Round

Calculus
Application of derivativesThe function f x 2x 36x 120z 11 has two critical numbers The smaller one is x and the larger one is x
Calculus
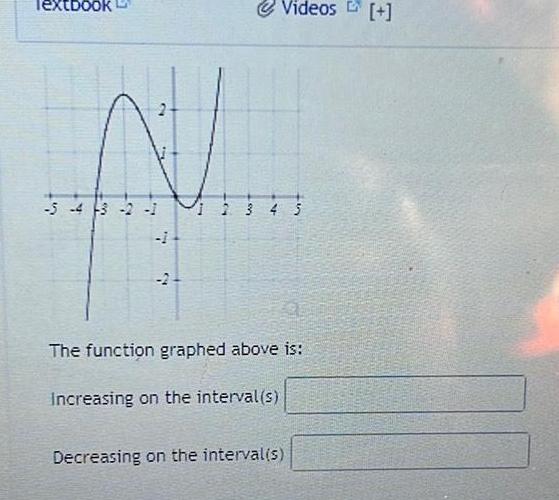
Application of derivativesTextbook 2 5 4 3 2 1 1 2 Videos 2 3 4 5 Increasing on the interval s ZOE The function graphed above is Decreasing on the interval s

Calculus
Application of derivatives14 1 point Solve each equation or inequality Check your solutions 221 O 1 C 3 h 1 No Solution 1
Calculus
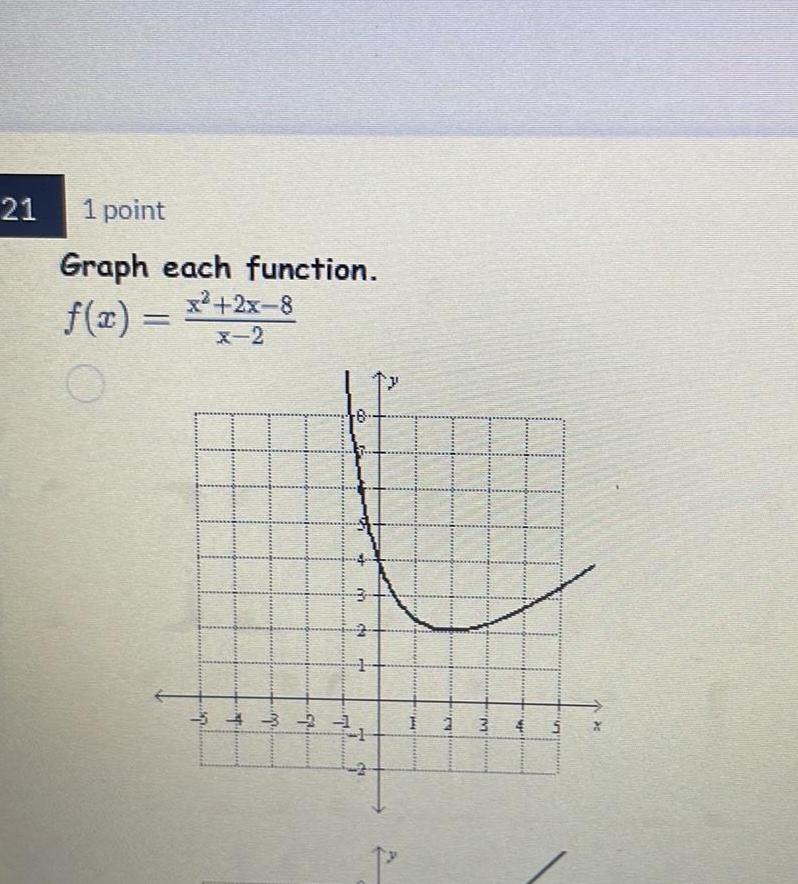
Application of derivatives21 1 point Graph each function x 2x 8 f x be F k 25 1 8 fo m da 1 H 24 www bt I 2 M 3 HA L be

Calculus
Application of derivativesThe smallest positive integer in the set 24x 60y 2000 x y ze ist a 2 b 4 c 6 d 24 swer A B