Application of derivatives Questions and Answers
Calculus
Application of derivativesse the appropriate reciprocal identity to find the value of tan 0 given that cot 0 2 5 0 Type an integer or a decimal
Calculus
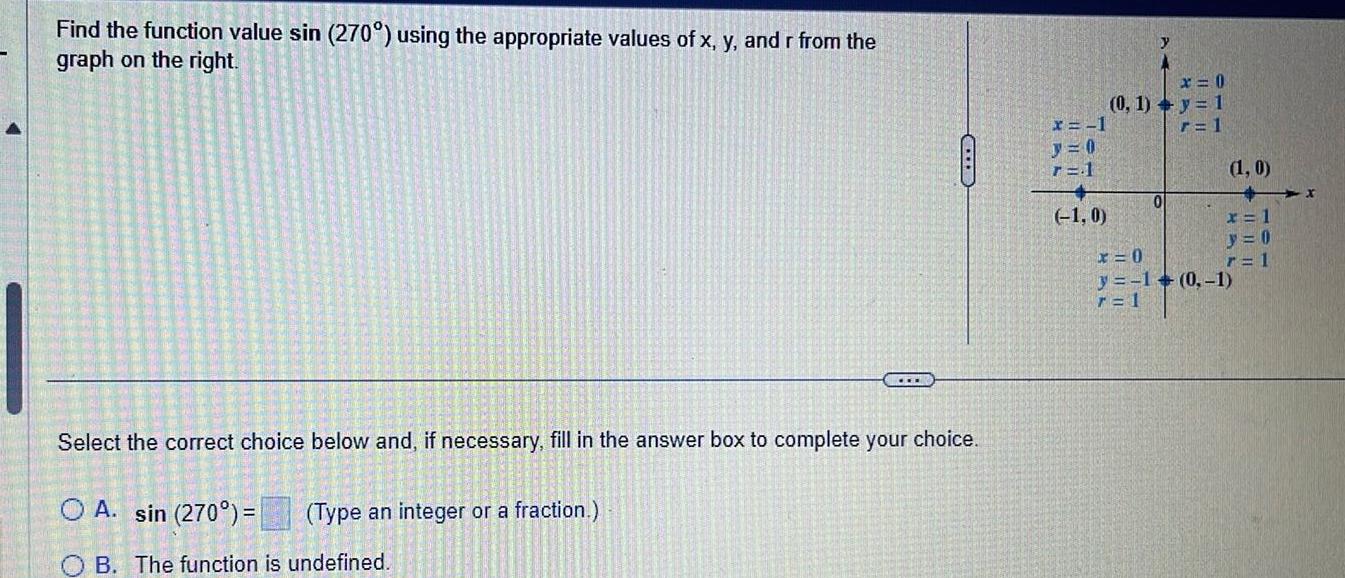
Application of derivativesFind the function value sin 270 using the appropriate values of x y and r from the graph on the right Select the correct choice below and if necessary fill in the answer box to complete your choice O A sin 270 Type an integer or a fraction CEL B The function is undefined x 1 r 1 1 0 y x 0 0 1 y 1 r 1 0 1 0 x x 1 y 0 r 1 x 0 y 1 0 1 7 1
Calculus
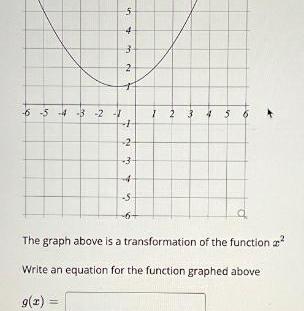
Application of derivativesLo 4 3 2 5 to 3 NO T 25 2 3 4 S I 2 3 4 5 6 q The graph above is a transformation of the function Write an equation for the function graphed above g x
Calculus
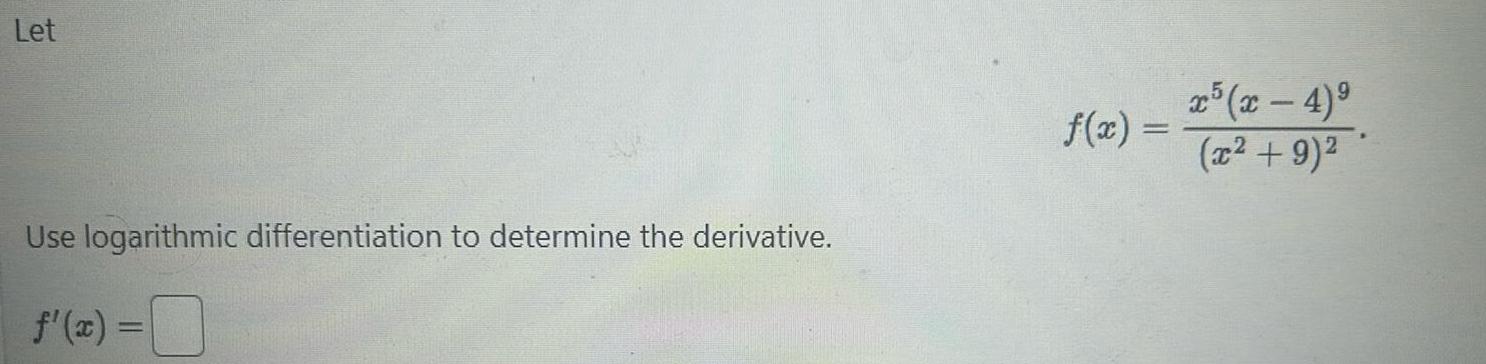
Application of derivativesLet Use logarithmic differentiation to determine the derivative f x f x x5 x 4 x 9

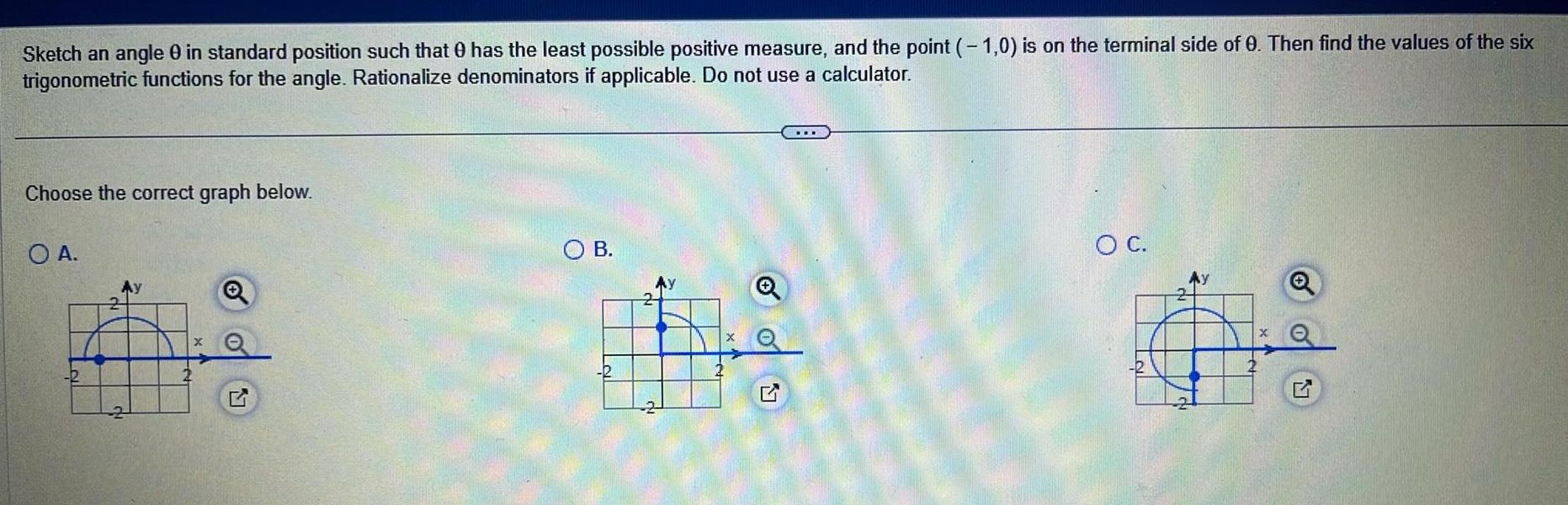
Calculus
Application of derivativesSketch an angle 0 in standard position such that has the least possible positive measure and the point 1 0 is on the terminal side of 0 Then find the values of the six trigonometric functions for the angle Rationalize denominators if applicable Do not use a calculator Choose the correct graph below O A Q O B 2 O C
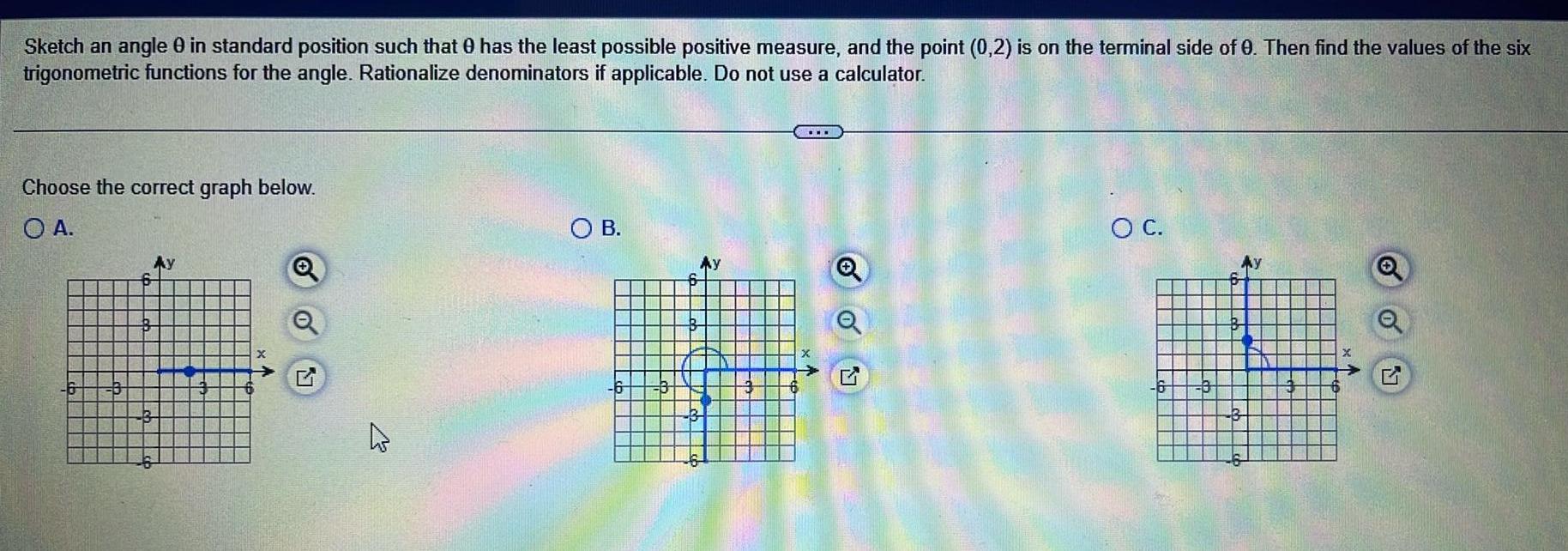
Calculus
Application of derivativesSketch an angle 0 in standard position such that has the least possible positive measure and the point 0 2 is on the terminal side of 0 Then find the values of the six trigonometric functions for the angle Rationalize denominators if applicable Do not use a calculator Choose the correct graph below O A N 4 OB 6 Ay O C 6 O
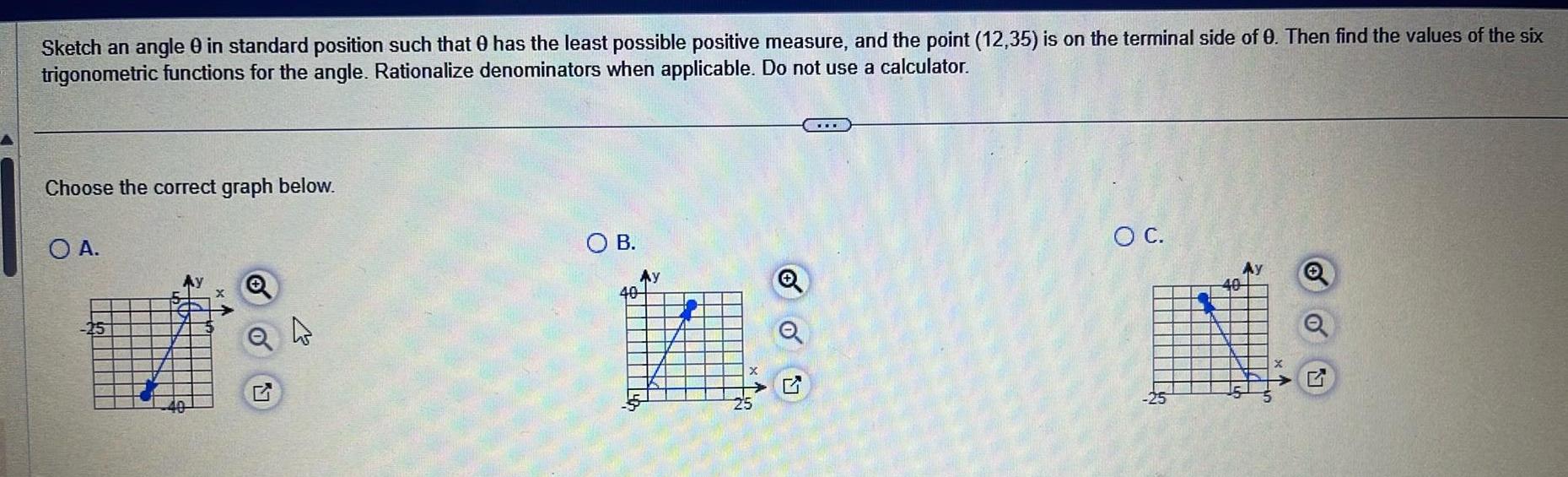
Calculus
Application of derivativesSketch an angle 0 in standard position such that has the least possible positive measure and the point 12 35 is on the terminal side of 0 Then find the values of the six trigonometric functions for the angle Rationalize denominators when applicable Do not use a calculator Choose the correct graph below O A 25 Q O B Ay 40 oo O C Ay Q
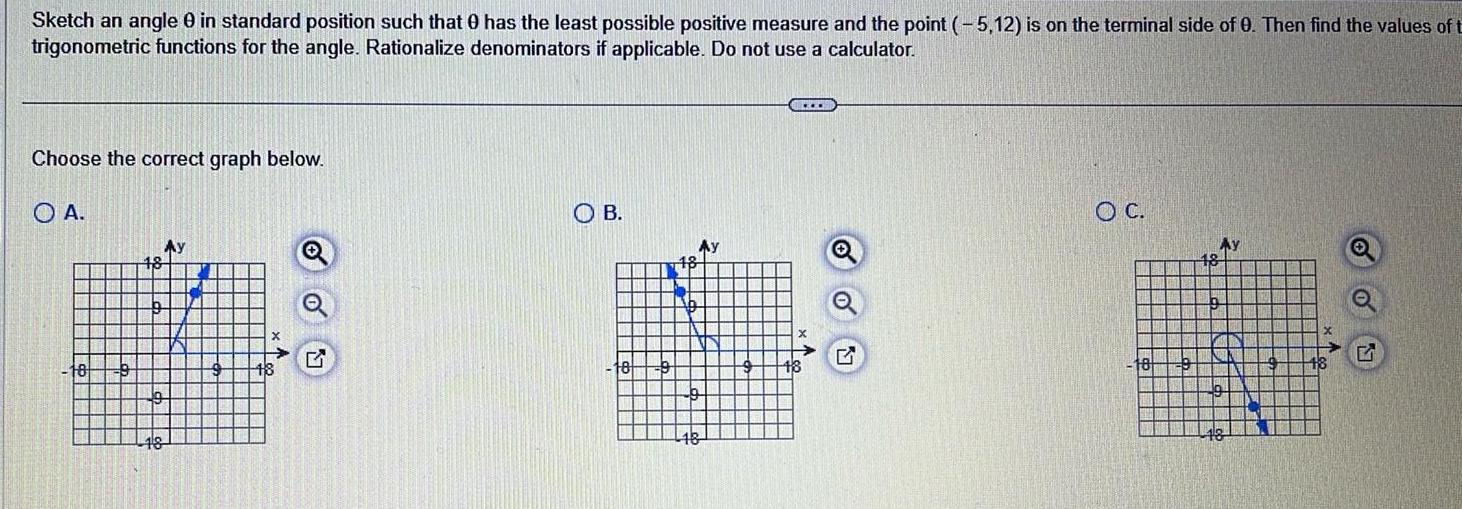
Calculus
Application of derivativesSketch an angle 0 in standard position such that has the least possible positive measure and the point 5 12 is on the terminal side of 0 Then find the values of t trigonometric functions for the angle Rationalize denominators if applicable Do not use a calculator Choose the correct graph below A 18 OB 117 Ay 1 OC 18 Q

Calculus
Application of derivativesThe value of e that satisty the conclusion of the mean value theorem for f x 1 3 Select one On 2 Ob 2 0 OC Od 3 Oe 3 NONE

Calculus
Application of derivativesWhich description applies to the graph of y3 7 7472 The graph is a translation 7 units right and 7 units up of the graph of y 3 7 The graph has an asymptote at y 7 The domain is all real numbers and the range is y 7 O The graph is a translation 7 units left and 7 units up of the graph of y 3 7 The graph has an asymptote at y 7 The domain is all real numbers and the range is y 7 O The graph is a translation 7 units left and 7 units down of the graph of y 3 7 The graph has an asymptote at y 7 The domain is all real numbers and the range is y 7 The graph is a translation 7 units night and 7 units down of the graph of y 3 7 The graph has an asymptote at y 7 The domain is all real numbers and the range is y 7
Calculus
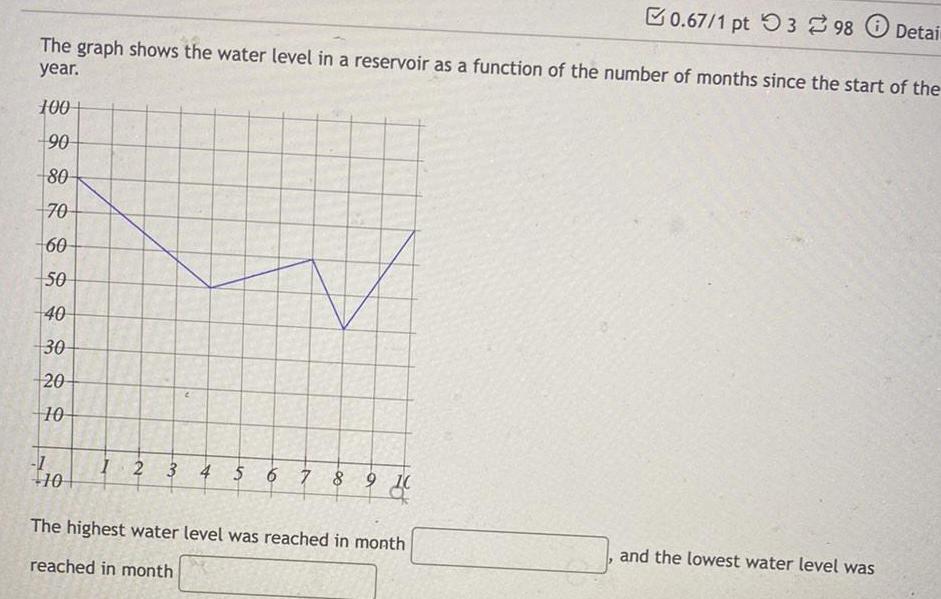
Application of derivatives0 67 1 pt 398 Detai The graph shows the water level in a reservoir as a function of the number of months since the start of the year 100 90 80 70 60 50 40 30 20 10 1 10 1 2 3 4 5 6 7 8 9 10 The highest water level was reached in month reached in month and the lowest water level was
Calculus
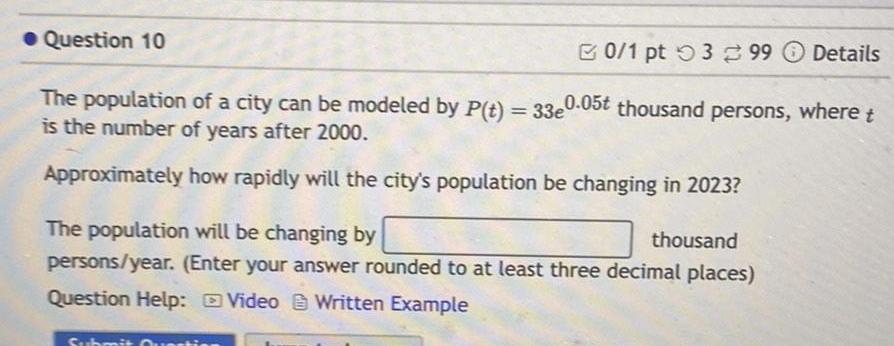
Application of derivativesQuestion 10 0 1 pt 399 Details The population of a city can be modeled by P t 33e0 05t thousand persons where t is the number of years after 2000 Approximately how rapidly will the city s population be changing in 2023 The population will be changing by thousand persons year Enter your answer rounded to at least three decimal places Question Help Video Written Example Subr

Calculus
Application of derivativesThe following chart shows living wage jobs in a city per 1000 working age adults over a 5 year period Year 1997 1998 1999 2000 2001 635 670 700 720 735 Jobs What is the average rate of change in the number of living wage jobs from 1997 to 1999 Note the units are already included Jobs Year
Calculus
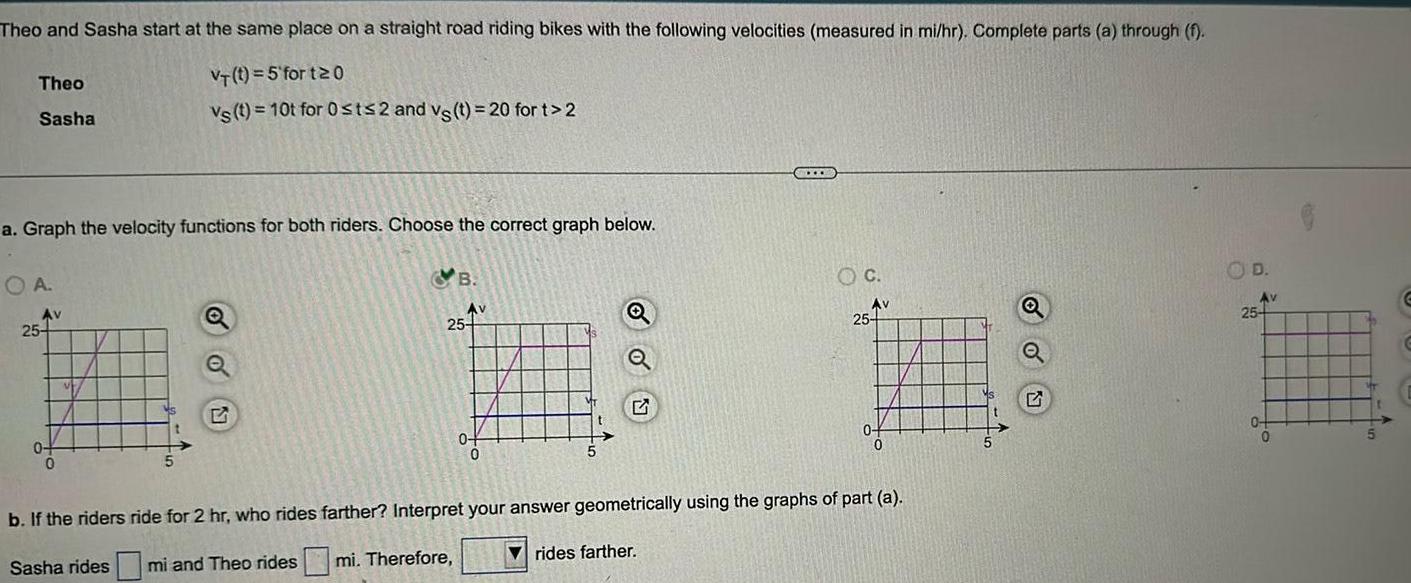
Application of derivativesTheo and Sasha start at the same place on a straight road riding bikes with the following velocities measured in mi hr Complete parts a through f VT t 5 fort 20 vs t 10t for 0 st 2 and vs t 20 for t 2 Theo Sasha a Graph the velocity functions for both riders Choose the correct graph below OA Av 25 0 0 5 B Av 25 0 OC rides farther Av 25 0 0 b If the riders ride for 2 hr who rides farther Interpret your answer geometrically using the graphs of part a Sasha rides mi and Theo ridesmi Therefore D Av 25 0
Calculus
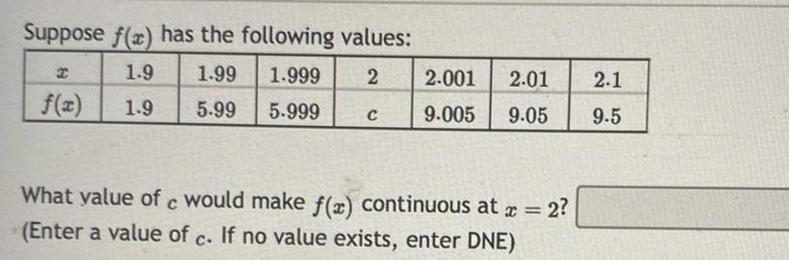
Application of derivativesSuppose f x has the following values I 1 9 1 99 1 999 2 1 9 5 99 5 999 C 2 001 2 01 2 1 9 005 9 05 9 5 What value of c would make f x continuous at x 2 Enter a value of c If no value exists enter DNE

Calculus
Application of derivativesSuppose f x is defined at 1 and lim f x exists but lim 4 1 1 The graph of y f z might look like select all that apply None of these f x f 1

Calculus
Application of derivativesLet f x 4x 3 if x 1 12 5x if x 1 Determine whether f x is continuous at x 1 If f x is not continuous identify why Not continuous lim x 1 f x f 1 Not continuous f 1 is undefined Not continuous lim f x does not exist x 1 The function is continuous at x 1
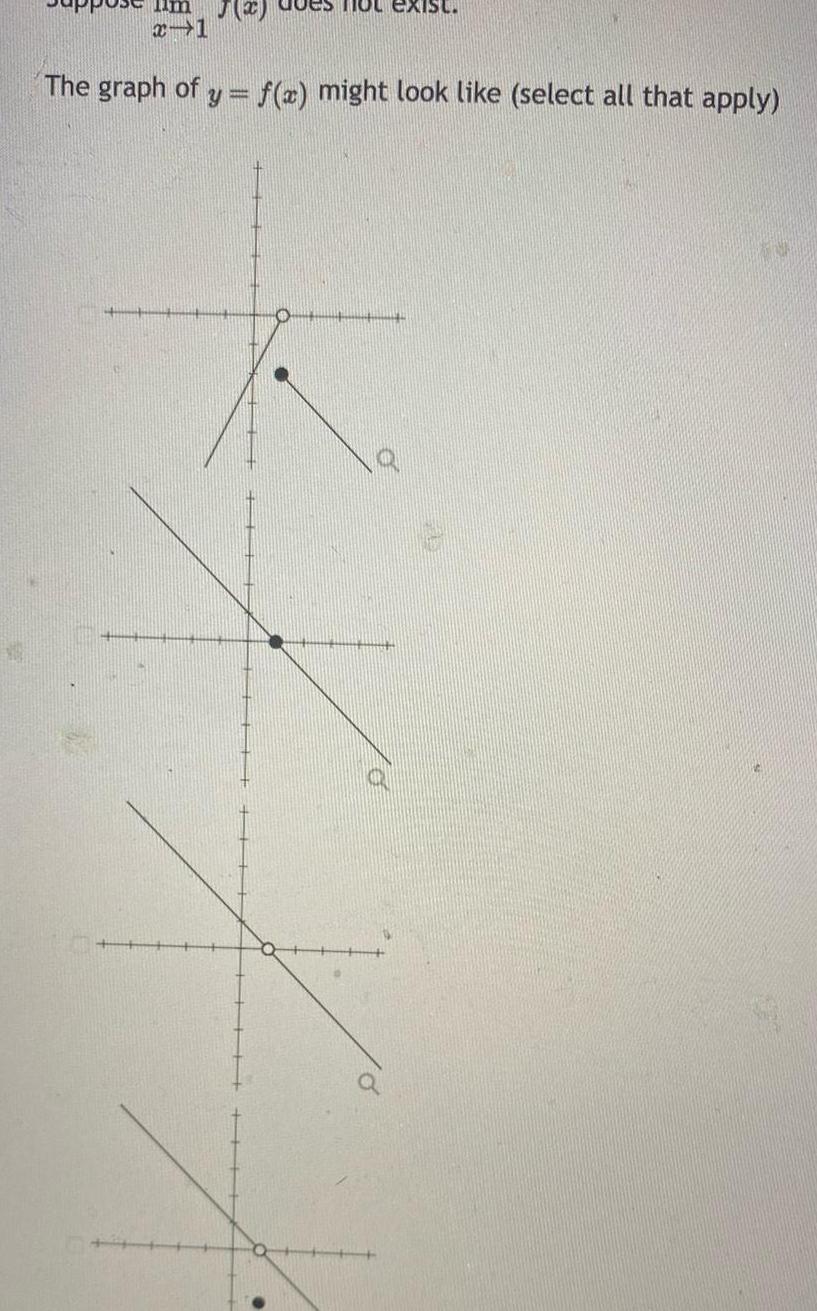
Calculus
Application of derivativesx 1 not exist The graph of y f x might look like select all that apply Q

Calculus
Application of derivativesThe graph below is the function f x 54 3 2 lim x 1 54327 lim x 1 2 he 72 S Find the following If no value exists enter DNE f x f x 12 lim f x x 1

Calculus
Application of derivativesThe graph of y f z has the following features e e f 2 1 lim f x 2 2 lim f x 2 2 2 Which of the following might be a graph of y y f x

Calculus
Application of derivativesDetermine the area of the given region The region bounded by y sin X 2 and y cos The area of the given region is Type an exact answer using radicalo X 2 on 3t 5t 2 2
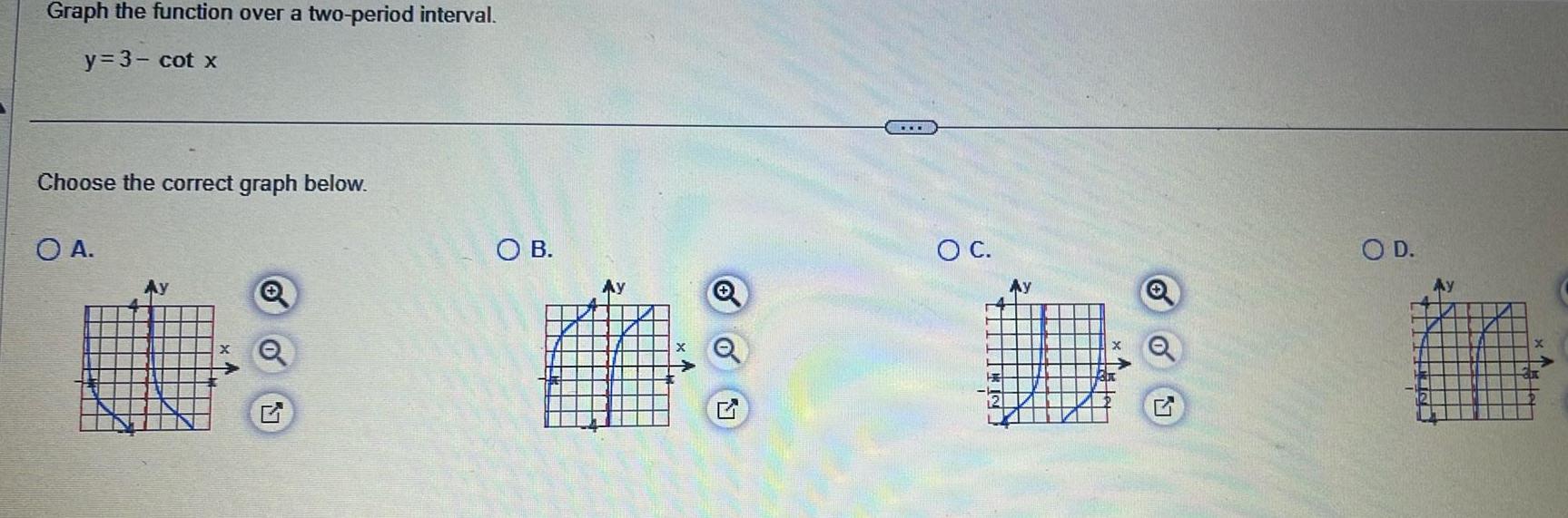
Calculus
Application of derivativesGraph the function over a two period interval y 3 cot x Choose the correct graph below O A OB Ay A O 17 O C Ay O D Ay
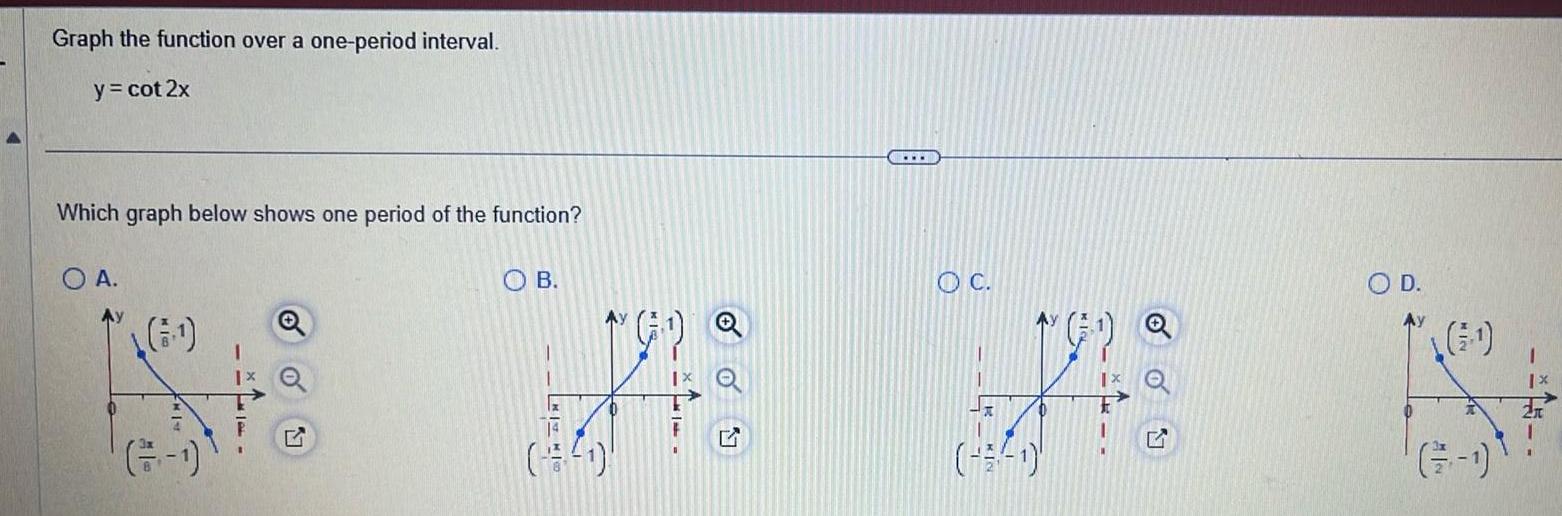
Calculus
Application of derivativesGraph the function over a one period interval y cot 2x Which graph below shows one period of the function O A 6 GF G B O C A O D Ay 6 1 1131
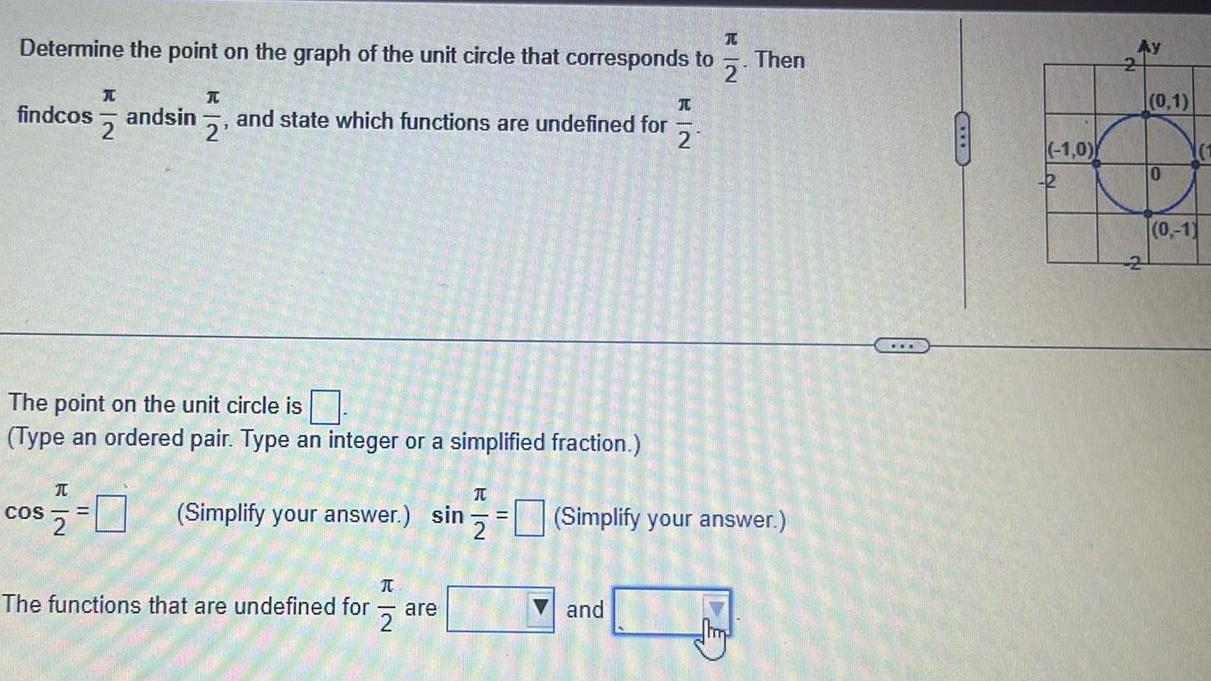
Calculus
Application of derivativesDetermine the point on the graph of the unit circle that corresponds to T findcos 2 andsin COS T and state which functions are undefined for The point on the unit circle is Type an ordered pair Type an integer or a simplified fraction The functions that are undefined for 2 2 are RIN and 2 T T 2 0 Simplify your answer sin Simplify your answer RIN 2 Then 1 0 2 Ay 2 0 1 10 1 0 1
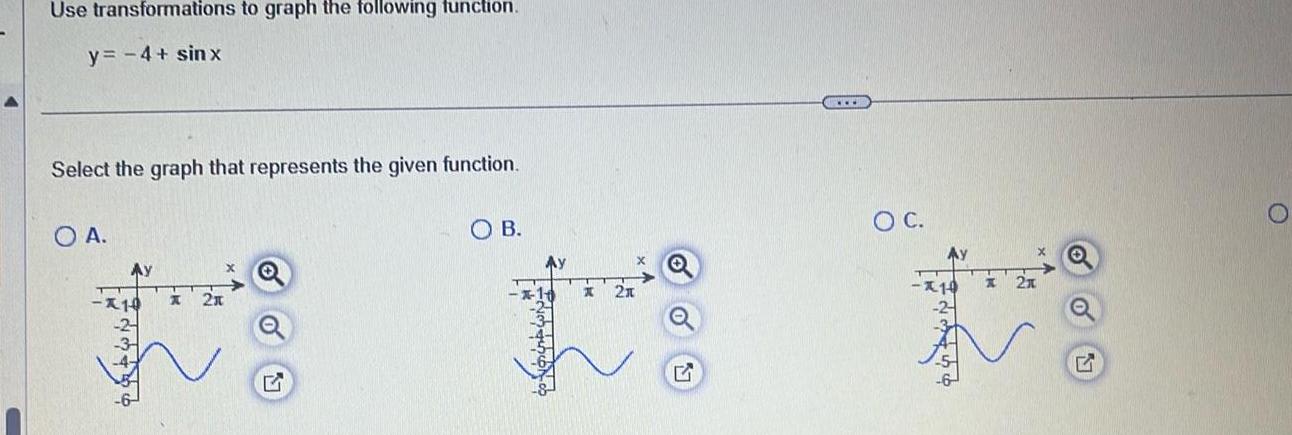
Calculus
Application of derivativesUse transformations to graph the following function y 4 sinx Select the graph that represents the given function O A Ay K 2x G OB K 2x G O C Ay 10 21 G O

Calculus
Application of derivativesCalculate the amount of work done to lift an object and cable Question How much work in foot pounds is done when a 45 foot long cable with a weight density of 7 pounds per foot is wound up 34 feet Do not include any units in your answer

Calculus
Application of derivativesThe concentration of a solution is defined as the amount of a substance divided by the volume of the solution Suppose a vat contains 18 kg of salt and 50 liters of water At t 0 water is added at a rate of 25 liters minute while salt is added at a rate of 9 kg minute A function giving the concentration after t minutes will be C t kg liter express as a function of t As time passes the concentration will Decrease Increase
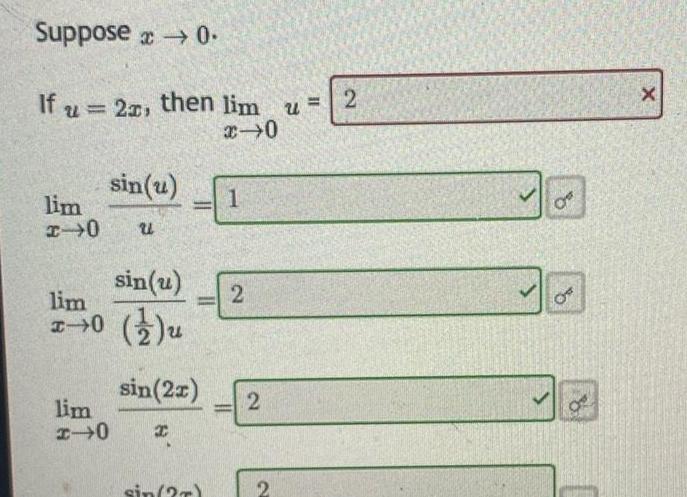
Calculus
Application of derivativesSuppose 0 If 2 then lim x 0 lim 0 lim sin u sin u 0 u lim H 0 U sin 2x I sin 2 1 2 2 2 U 2 OF OF X
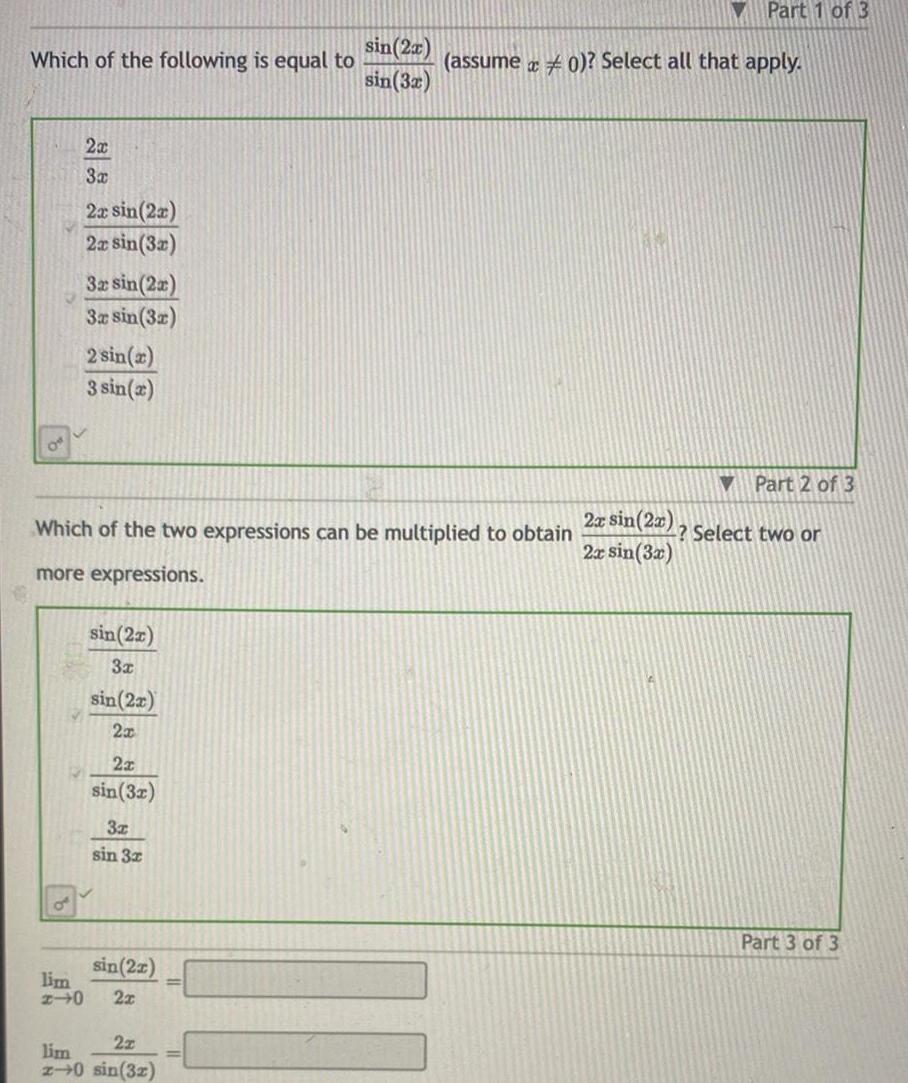
Calculus
Application of derivativesWhich of the following is equal to 2x 3x 2x sin 2x 2x sin 3x 3x sin 2x 3x sin 3x 2 sin x 3 sin x sin 2x 3x sin 2x 2x Which of the two expressions can be multiplied to obtain more expressions 2x sin 3x 3x sin 3x sin 2x lim 2 0 2x sin 2x sin 3x 2z lim 2 0 sin 32 assume x0 Select all that apply Part 1 of 3 2x sin 2x 2x sin 3x Part 2 of 3 Select two or Part 3 of 3
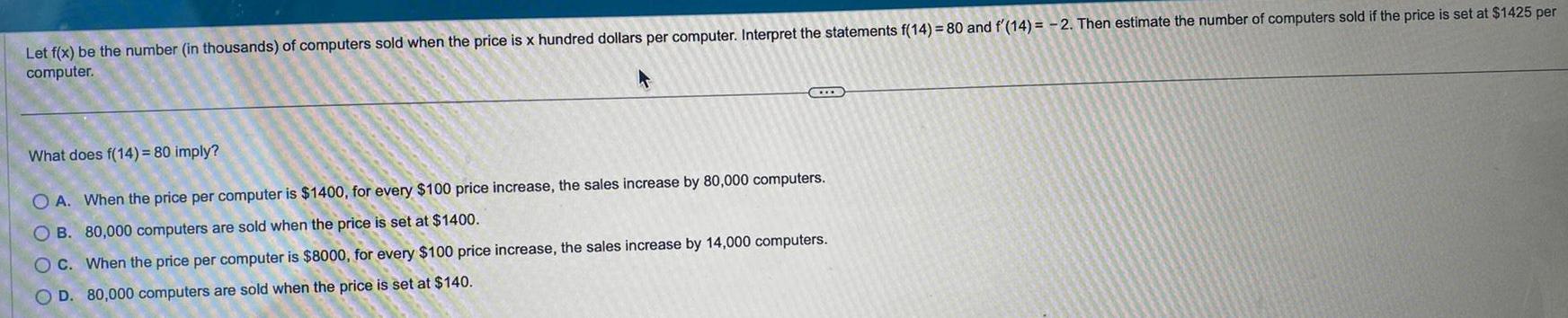
Calculus
Application of derivativesLet f x be the number in thousands of computers sold when the price is x hundred dollars per computer Interpret the statements f 14 80 and f 14 2 Then estimate the number of computers sold if the price is set at 1425 per computer T What does f 14 80 imply O A When the price per computer is 1400 for every 100 price increase the sales increase by 80 000 computers OB 80 000 computers are sold when the price is set at 1400 OC When the price per computer is 8000 for every 100 price increase the sales increase by 14 000 computers OD 80 000 computers are sold when the price is set at 140
Calculus
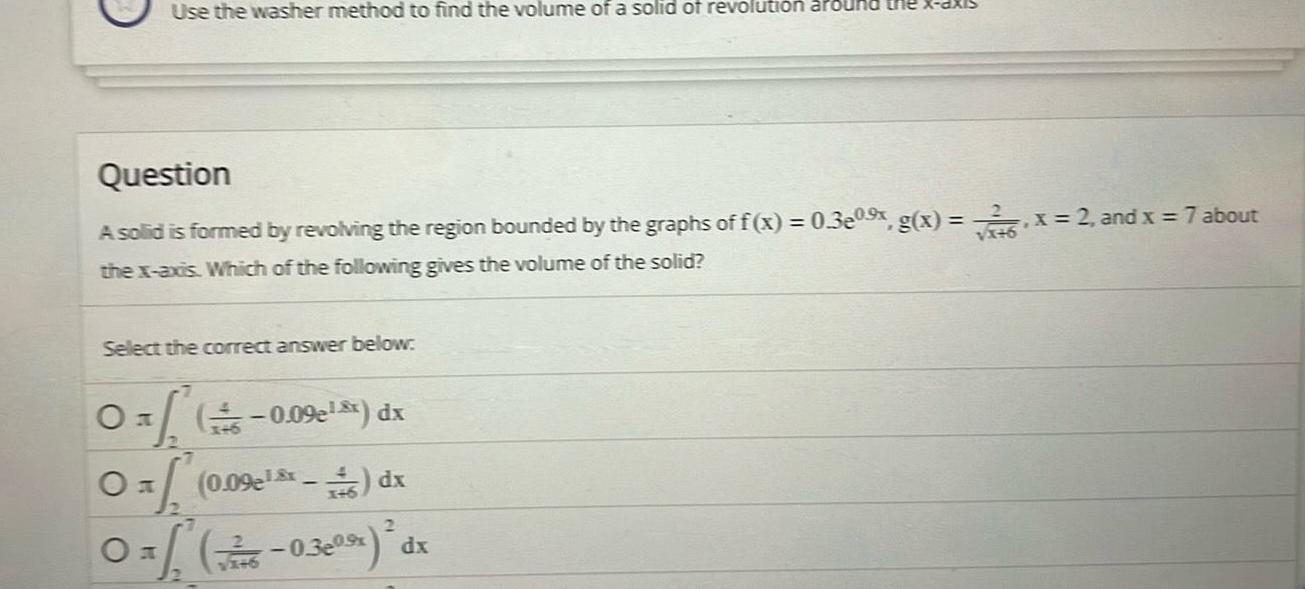
Application of derivativesUse the washer method to find the volume of a solid of revolution around Question 2 A solid is formed by revolving the region bounded by the graphs of f x 0 3e0 x g x x 2 and x 7 about the x axis Which of the following gives the volume of the solid Select the correct answer below Oxf 0 09e xx dx 0 0 09e 46 dx 2 0 6 0 3e0 dx
Calculus
Application of derivativesAn object moving in a straight line travels s t kilometers in t hours where s t 7t 5t a What is the object s velocity when t 6 b How far has the object traveled in 6 hours c When is the object traveling at a rate of 6 km h a The object s velocity when t 6 is km h
Calculus
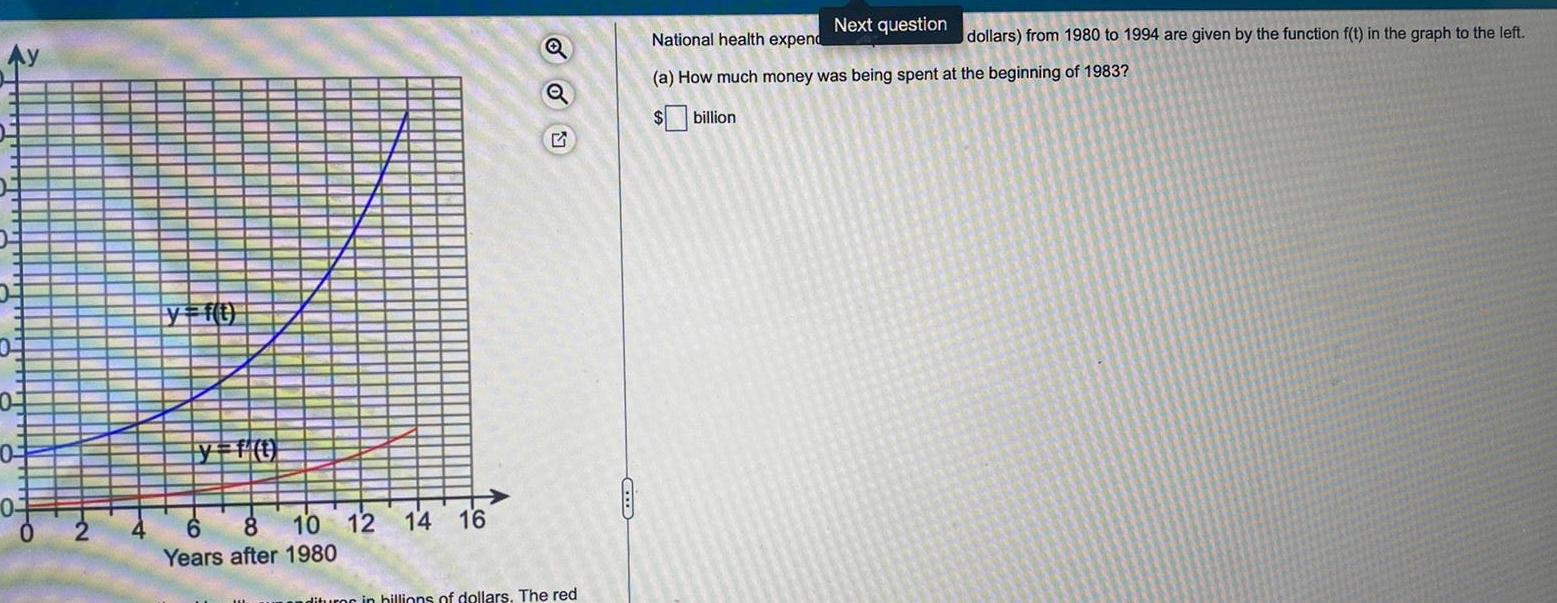
Application of derivativesAy 01 0 3 0 y f t y f t 10 12 14 16 8 Years after 1980 Q OU Q ndituror in billions of dollars The red Next question National health expend dollars from 1980 to 1994 are given by the function f t in the graph to the left a How much money was being spent at the beginning of 1983 billion

Calculus
Application of derivativesLet f t be the temperature of a cup of coffee t minutes after it has been poured Interpret f 8 110 and f 8 5 Estimate the temperature of the coffee after 8 minutes and 42 seconds that is after 8 7 minutes C What does f 8 110 imply OA 8 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 110 degrees per minute B 110 minutes after the coffee has been poured the temperature of the cup of coffee is 8 degrees O C 110 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 8 degrees per minute OD 8 minutes after the coffee has been poured the temperature of the cup of coffee is 110 degrees
Calculus
Application of derivativesSuppose that f x x a What is the average rate of change of f x over each of the following intervals 3 to 4 3 to 3 5 3 and to 3 1 b What is the instantaneous rate of change of f x when x 3 a The average rate of change of f x over the interval 3 to 4 is Simplify your answer
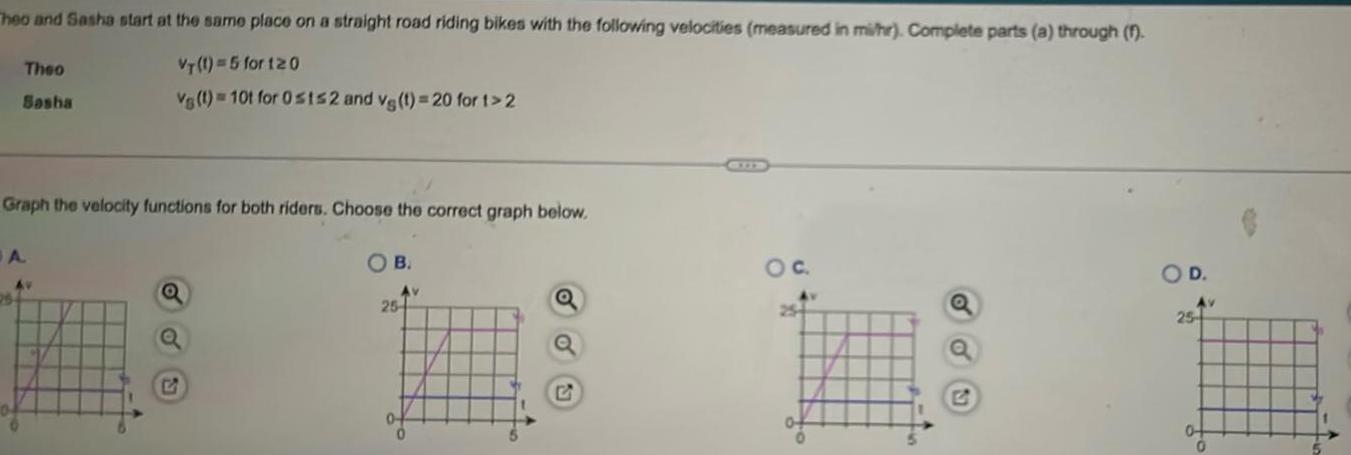
Calculus
Application of derivativesTheo and Sasha start at the same place on a straight road riding bikes with the following velocities measured in mi hr Complete parts a through f VT 1 5 for 120 Vg t 10t for Osts2 and vg t 20 for 1 2 Theo Sasha Graph the velocity functions for both riders Choose the correct graph below JA 25 Av Q C OB Av 25 04 OC O D 25 Av
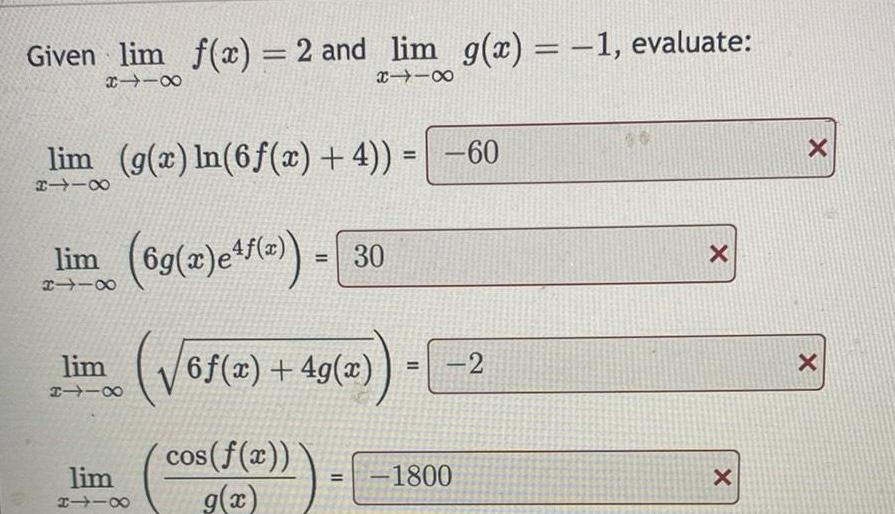
Calculus
Application of derivativesGiven lim f x 2 and lim g x 1 evaluate 8118 X118 lim g x ln 6f x 4 60 8118 lim 69 x e f z 30 8118 lim 8118 lim 8118 6f x 49 a cos f x g x 11 2 1800 20 X X X X
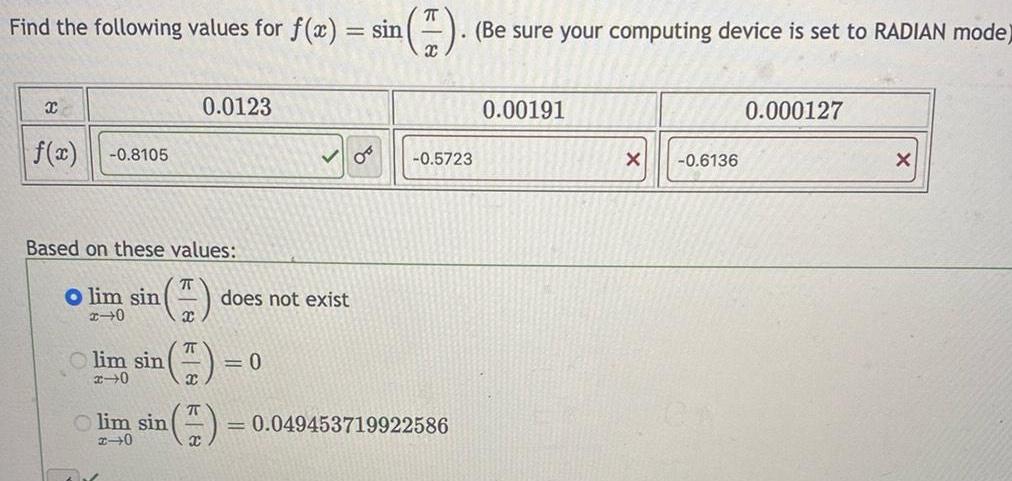
Calculus
Application of derivativesFind the following values for f x sin Be sure your computing device is set to RADIAN mode X f x 0 8105 Based on these values O lim sin x 0 lim sin x 0 Olim sin x 0 0 0123 70 X 05 does not exist 0 X 0 5723 0 049453719922586 0 00191 X 0 6136 0 000127 X
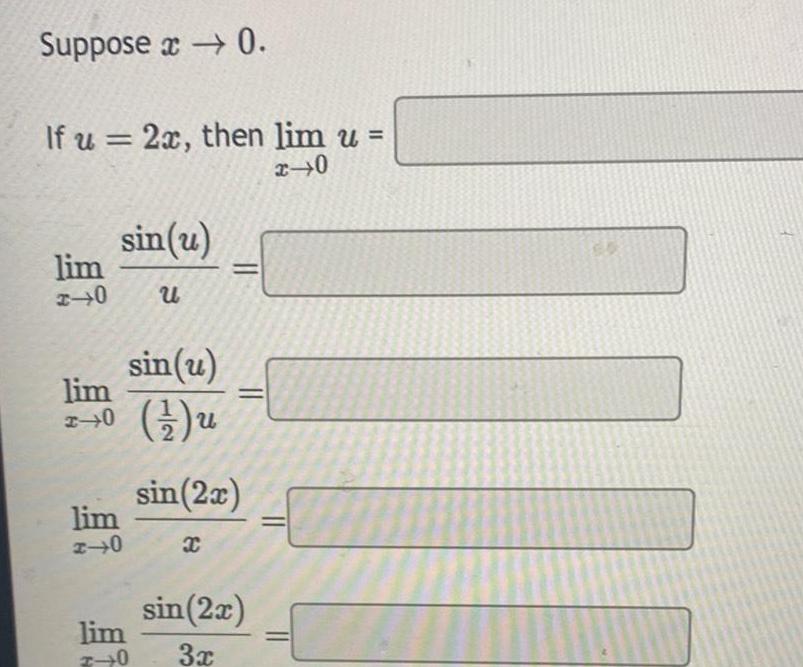
Calculus
Application of derivativesSuppose 0 If u 2x then lim u x 0 lim 1 0 lim I 0 lim A 0 sin u u lim 0 sin u 1 u sin 2x x sin 2x 3x
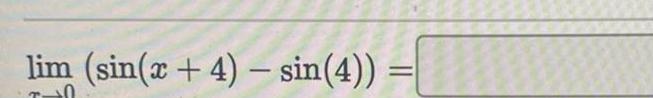
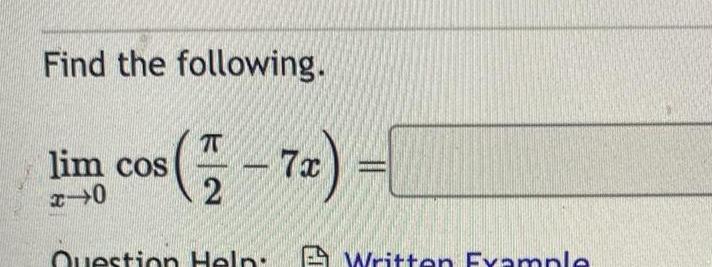
Calculus
Application of derivativesFind the following lim cos 72 7x x 0 Question Help Written Example
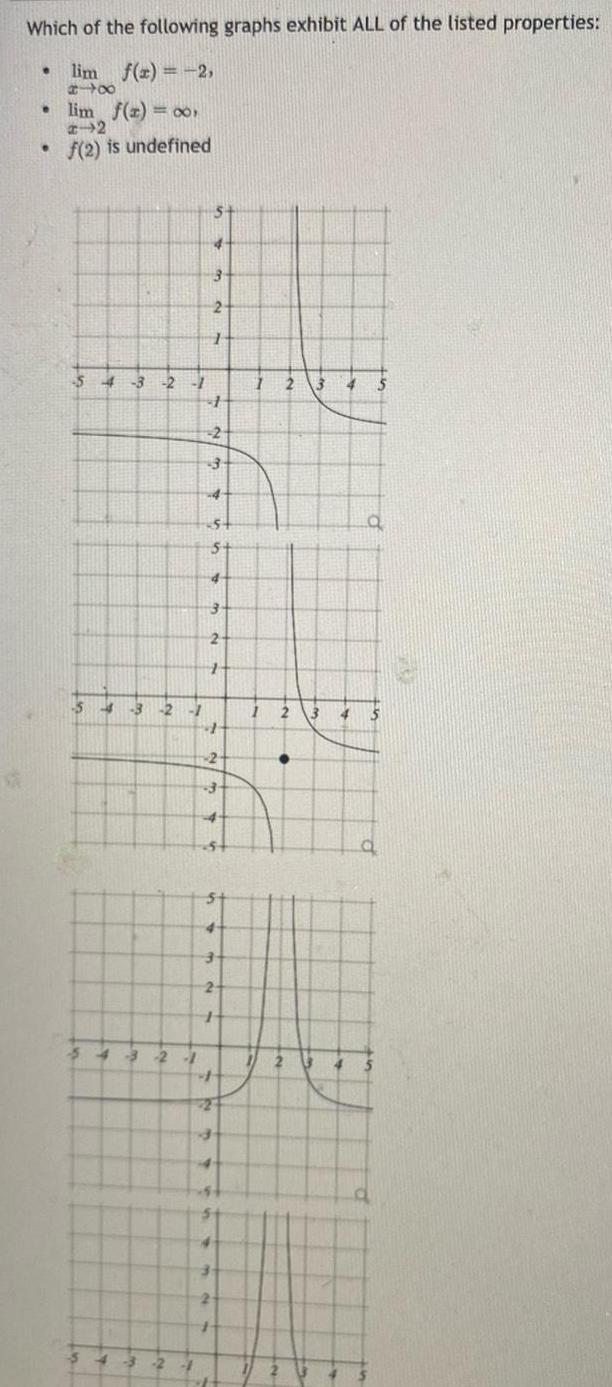
Calculus
Application of derivativesWhich of the following graphs exhibit ALL of the listed properties lim f x 2 818 lim f t o 2 f 2 is undefined 54 3 2 1 54 3 2 1 54 3 2 1 4 3 2 4 S 4 3 2 1 2 4 S 5 4 3 2 1 1 2 3 5 3 2 P DE 1 1 2 34 5 2 a 3 4 2 B q 70
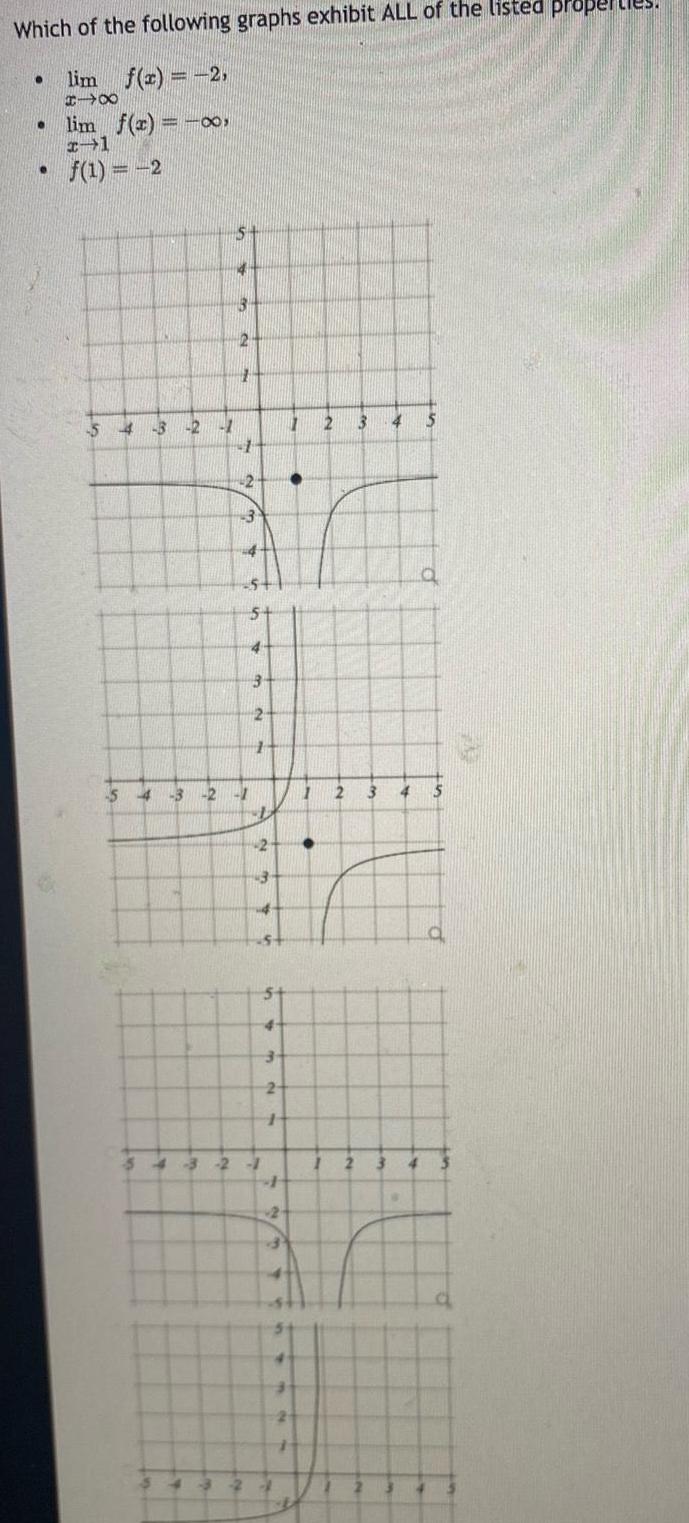
Calculus
Application of derivativesWhich of the following graphs exhibit ALL of the listed proper lim f x 2 HIX lim f x 00 I 1 f 1 2 54 3 2 1 51 4 13 2 1 1 2 3 4 54 5 54 3 2 1 4 3 2 1 2 3 4 st 3 2 54 3 2 1 2 1 2 3 1 2 3 4 5 La 4 5 1 2 3 4 a
Calculus
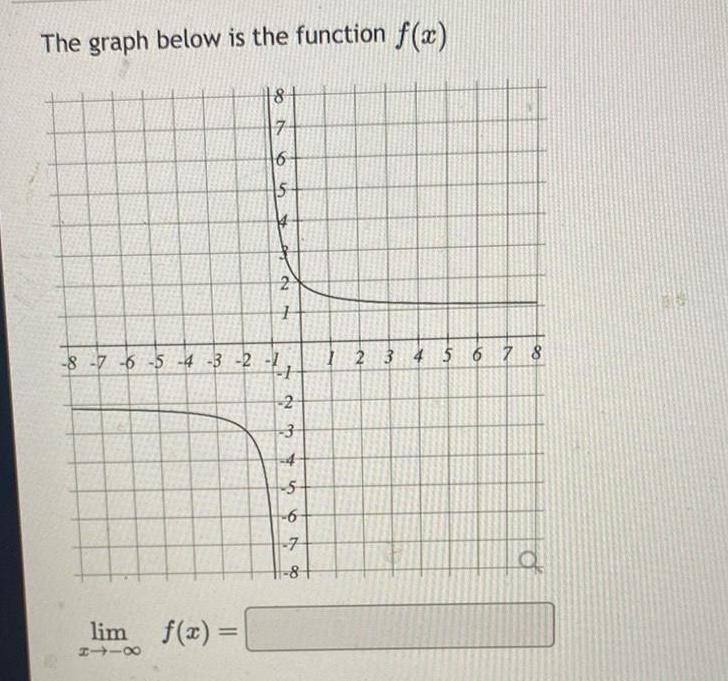
Application of derivativesThe graph below is the function f x 8 7 16 15 lim f x 8118 2 1 8 7 6 5 4 3 2 1 2 3 34 4 5 56400 6 7 8 1 2 3 4 5 6 7 8
Calculus
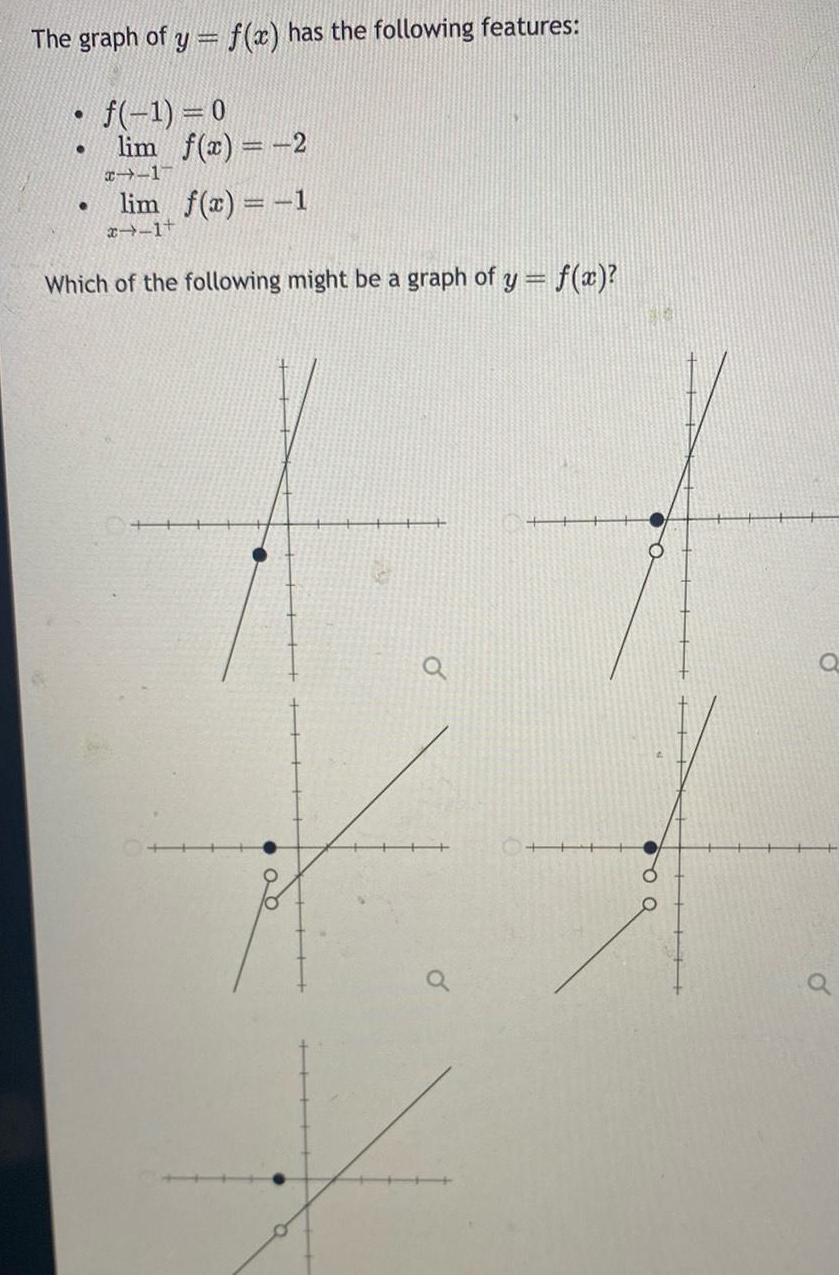
Application of derivativesThe graph of y f x has the following features f 1 0 lim f x 2 x 1 lim f x 1 1 Which of the following might be a graph of y f x a Q a

Calculus
Application of derivatives12 If the function f is continuous for all real numbers and if when x 3 then f 3 f x x 6x 9 x 3

Calculus
Application of derivativesSuppose a student finds the following values of x and f x x If f 4 9 3 4 99 877 C 4 999 2393 these values would SUPPORT the claim that lim f x x 5
Calculus
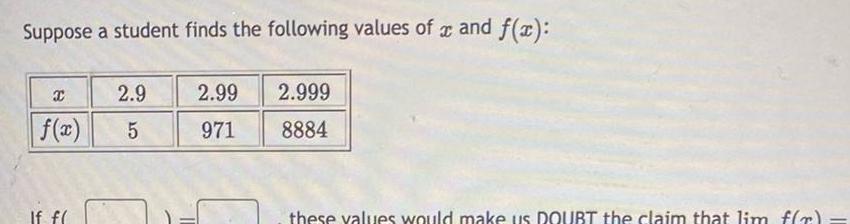
Application of derivativesSuppose a student finds the following values of x and f x X 2 9 f x 5 If f 2 99 971 2 999 8884 these values would make us DOUBT the claim that lim f x
Calculus
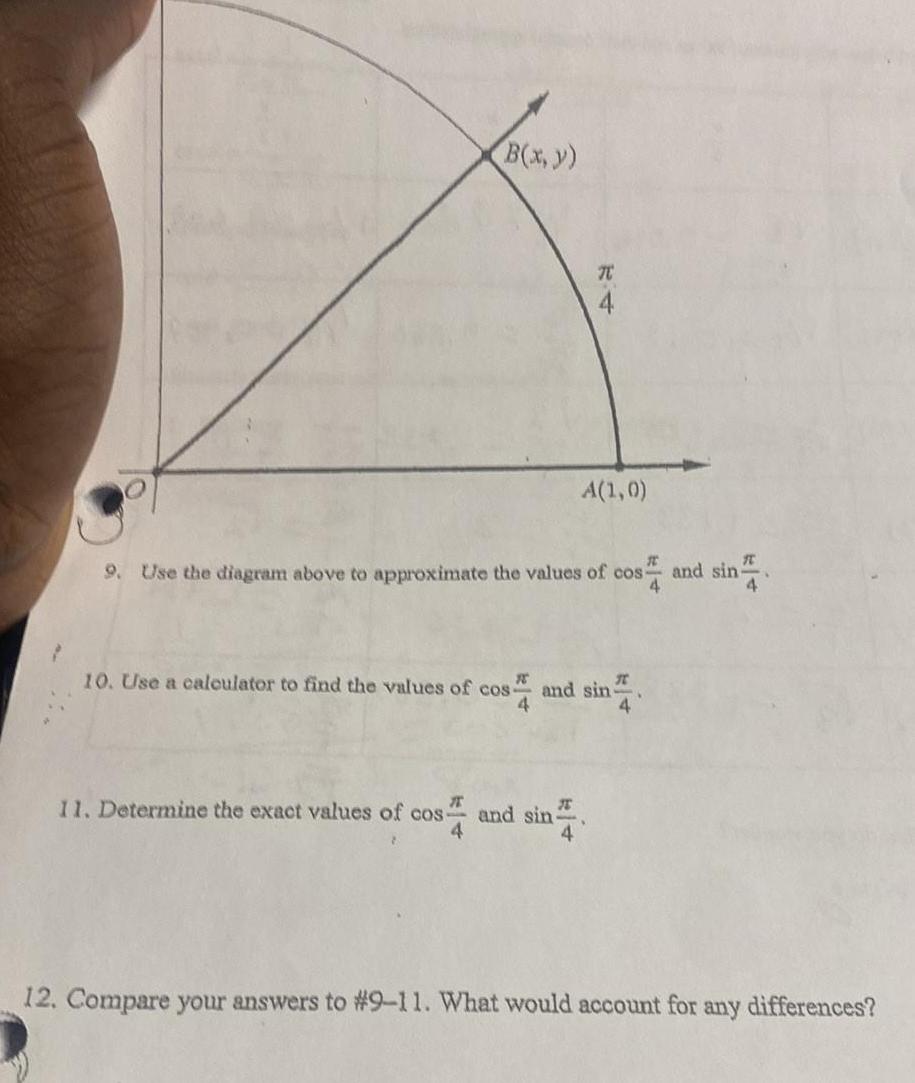
Application of derivativesB x y 11 Determine the exact values of cos I 4 TC 4 T 9 Use the diagram above to approximate the values of cosand sin 4 A 1 0 10 Use a calculator to find the values of cos and sin 4 4 and sin 4 12 Compare your answers to 9 11 What would account for any differences