Definite Integrals Questions and Answers
Calculus
Definite IntegralsHow many integers satisfy the inequality x2 4 x2 10 0 Onone Otwo four an infinite number
Calculus
Definite IntegralsFind the average value of f x 2 sin x 6 cos z on the interval 0 Average value

Calculus
Definite IntegralsA carpenter is building an open box with a square base for holding firewood The box must have a surface area of 8 m What dimensions will yield the maximum volume

Calculus
Definite IntegralsThe decay rate k for a particular radioactive element is 2 1 where time is measured in years Find the half life of the element
Calculus
Definite IntegralsScore 2 8 2 8 answered Question 7 Find the area of a triangle bounded by the y axis the line f x 6 f x that passes through the origin Area Question Help Video Message instructor 5 7 and the line perpendicular to

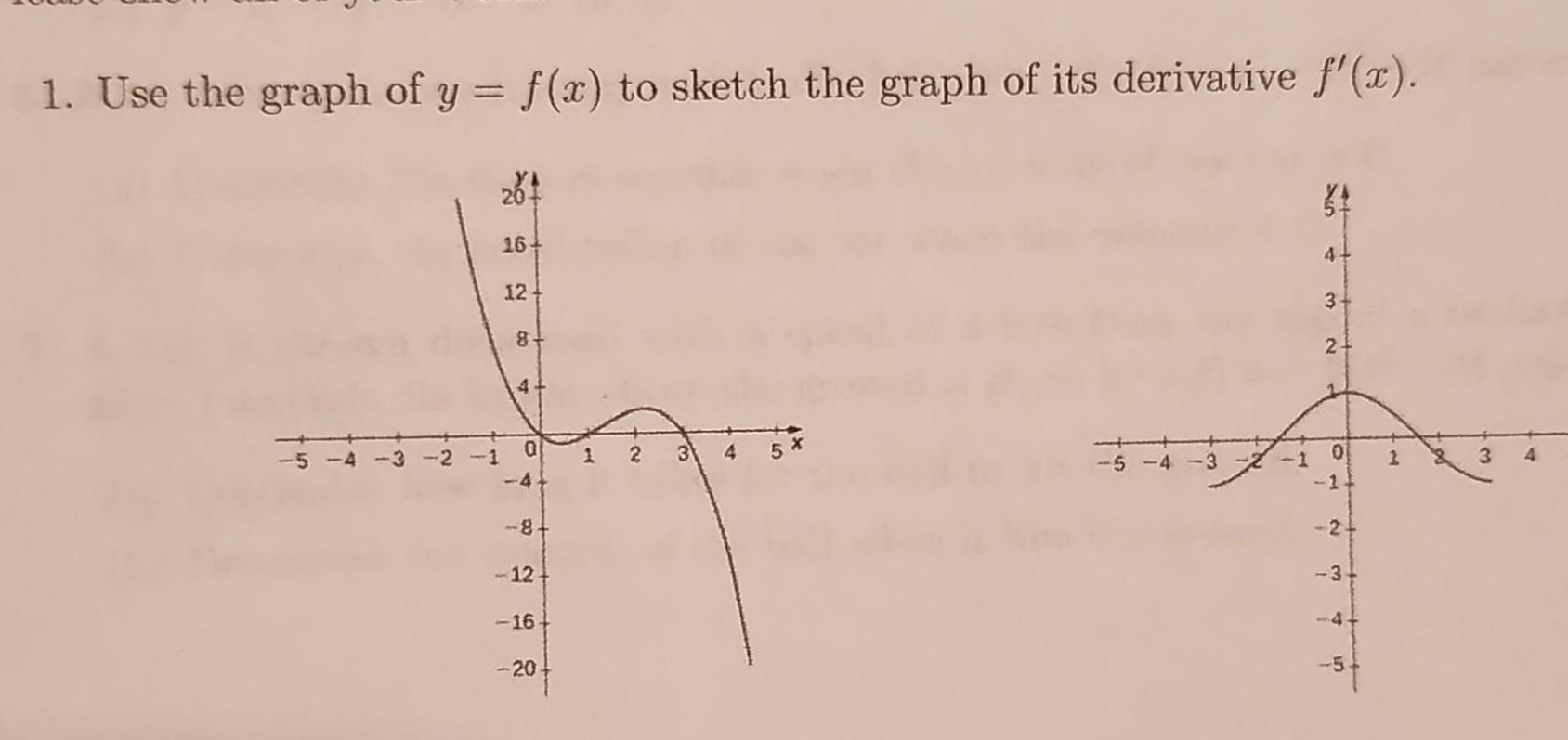
Calculus
Definite Integrals1 Use the graph of y f x to sketch the graph of its derivative f x 20 16 124 8 4 0 4 8 12 16 20 2 3 A 5 4 3 1 1 34 3 2 O T 2 3 4 in M 3 4
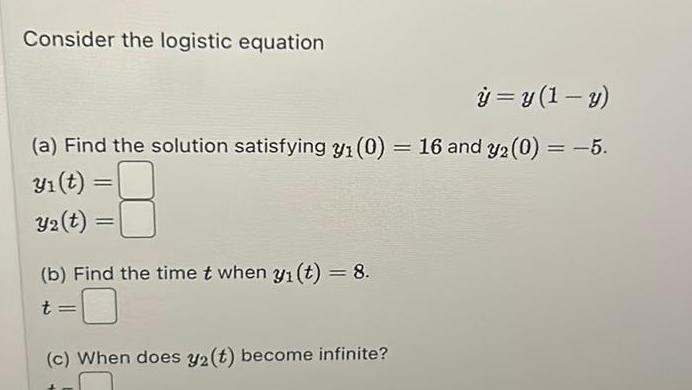
Calculus
Definite IntegralsConsider the logistic equation y y 1 y a Find the solution satisfying y 0 16 and y2 0 5 3 t Y2 t b Find the time t when y t 8 t c When does y2 t become infinite
Calculus
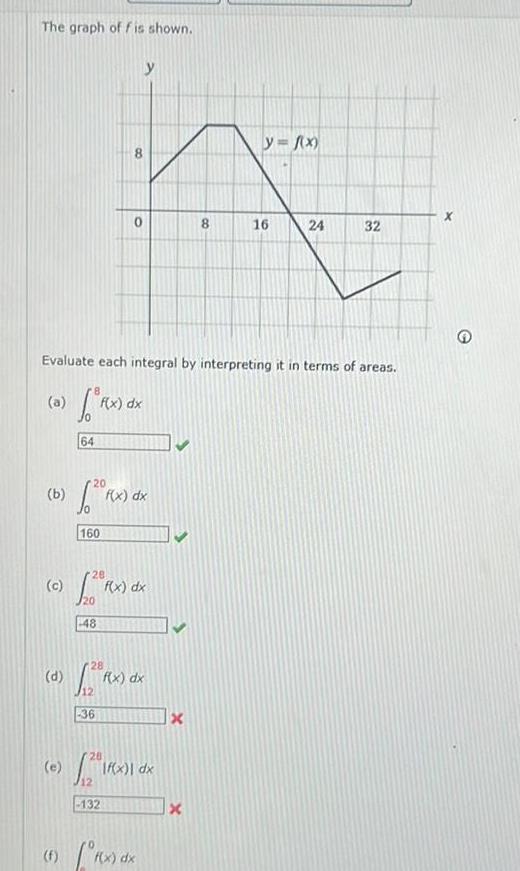
Definite IntegralsThe graph of f is shown b d Evaluate each integral by interpreting it in terms of areas a f x dx e 64 20 160 y f x A 8 16 24 48 28 20 RX f x dx 132 8 28 FX 12 36 f x dx 28 12 1Rx f x dx If x dx f f x dx Xx 32 x
Calculus
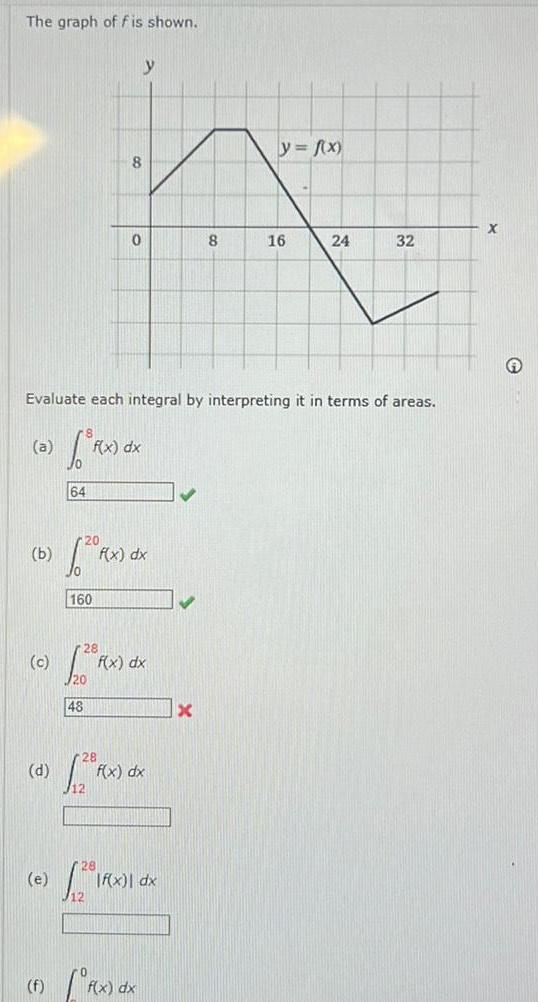
Definite IntegralsThe graph of f is shown b c d e f 64 Evaluate each integral by interpreting it in terms of areas a Rx dx 20 160 48 8 28 0 F f x dx 28 f x dx f x dx 2 1Rx dx f x dx 8 x y f x 16 24 32 X


Calculus
Definite IntegralsGraphy 22 12 x2 and y Select each correct answer on the same axes Which do you think is larger x3 1 dx is greater because the area under y is greater than the area under the graph of y S 23 1 1 6 12 1 2 dx is greater because the area under y dx is greater because the area under y S dx is greater because the graph of y 1 3 dx ordx Why dx is greater because the graph of y dx is greater because the graph of y 1 1 is greater than the area under the graph of y x3 1 is less than the area under the graph of y x 1 is above greater than the graph of y x2 1 is below less than the graph of y is above greater than the graph of y x3 x x2

Calculus
Definite IntegralsThe acceleration function in m s2 and the initial velocity v 0 in m s are given for a particle moving along a line a t 2t 2 v 0 15 Ost 5 a Find the velocity in m s at time t m s b Find the distance traveled in m during the given time interval m

Calculus
Definite IntegralsTheorem If f is integrable on a b then f x dx heorem f x dx lim f x 4x 118 where Ax and x a iAx Use the given theorem to evaluate the definite integral b a n x2 4x 7 dx
Calculus
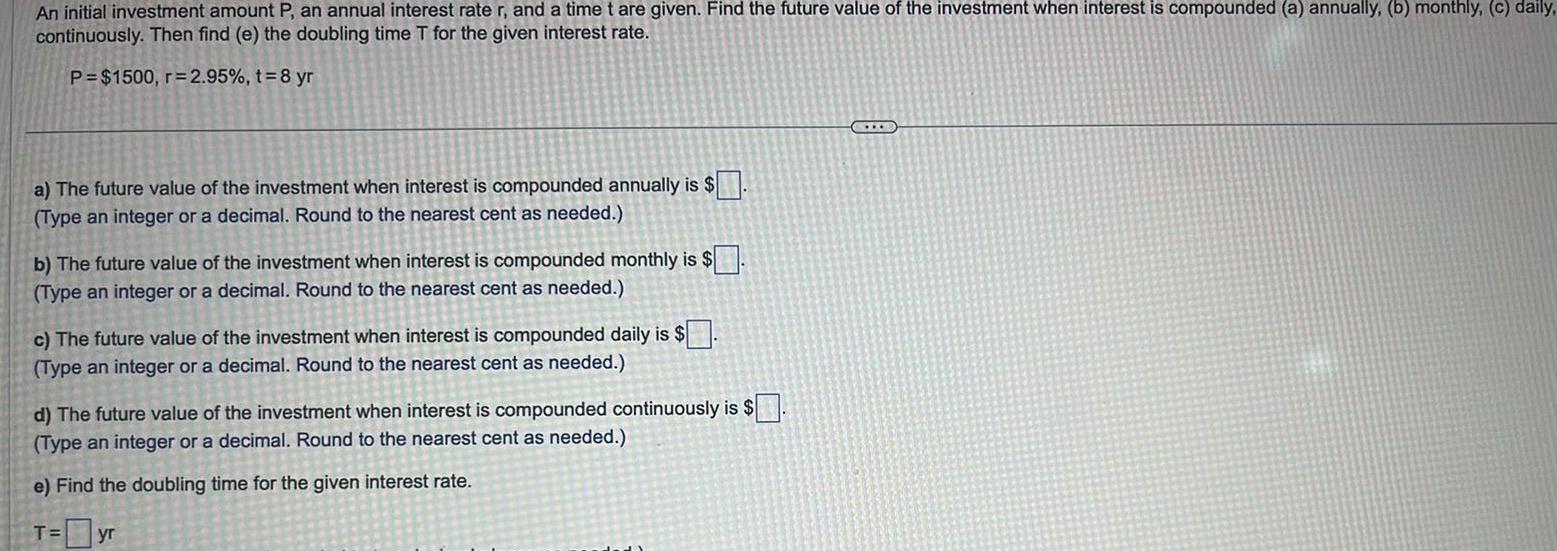
Definite IntegralsAn initial investment amount P an annual interest rate r and a time t are given Find the future value of the investment when interest is compounded a annually b monthly c daily continuously Then find e the doubling time T for the given interest rate P 1500 r 2 95 t 8 yr a The future value of the investment when interest is compounded annually is Type an integer or a decimal Round to the nearest cent as needed b The future value of the investment when interest is compounded monthly is Type an integer or a decimal Round to the nearest cent as needed c The future value of the investment when interest is compounded daily is Type an integer or a decimal Round to the nearest cent as needed d The future value of the investment when interest is compounded continuously is Type an integer or a decimal Round to the nearest cent as needed e Find the doubling time for the given interest rate T yr C

Calculus
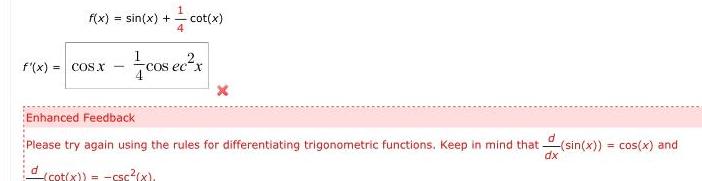
Definite Integralsf x COS X f x sin x cot 4 d cot x cos ec x Enhanced Feedback Please try again using the rules for differentiating trigonometric functions Keep in mind that sin x cos x and dx cot x csc x

Calculus
Definite IntegralsUse an appropriate substitution and then a trigonometric substitution to evaluate the integral In 3 S 0 In 3 S 0 e dt 2t 4 e dt 2t ve 4 11
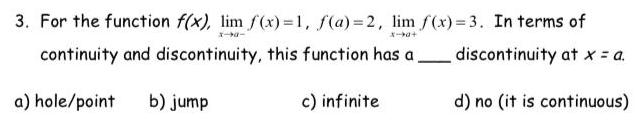
Calculus
Definite Integrals3 0 3 b0 3 For the function f x lim f x 1 f a 2 lim f x 3 In terms of continuity and discontinuity this function has a discontinuity at x a a hole point b jump c infinite d no it is continuous

Calculus
Definite Integrals2 Find a center of mass of a thin plate of density 8 6 bounded by the lines y x and x 0 and the parabola y 2 x the first quadrant x 0 y 0 Type simplified fractions
Calculus
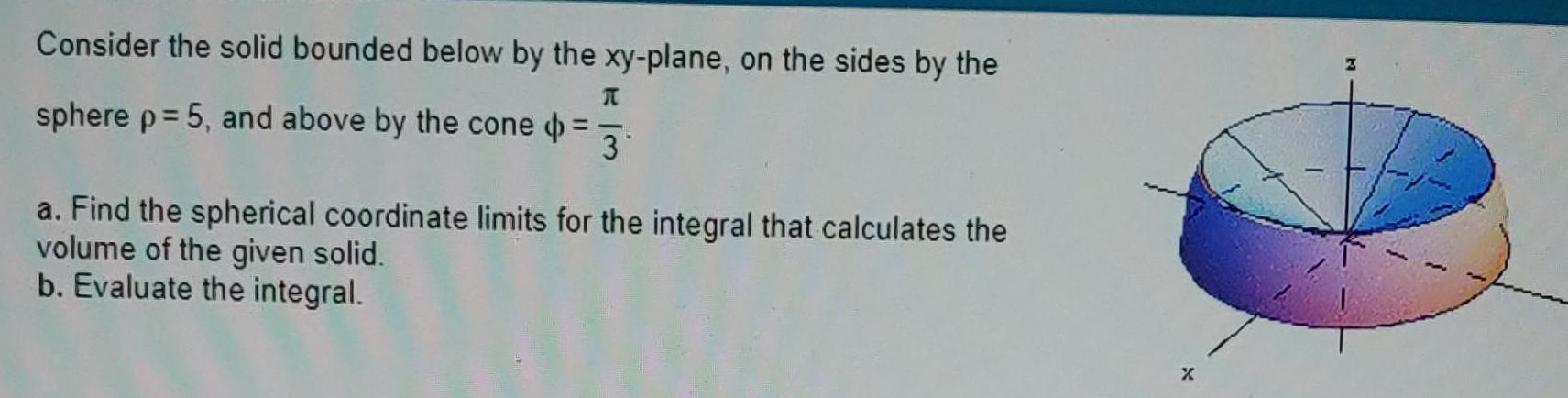
Definite IntegralsConsider the solid bounded below by the xy plane on the sides by the sphere p 5 and above by the cone 3 a Find the spherical coordinate limits for the integral that calculates the volume of the given solid b Evaluate the integral X
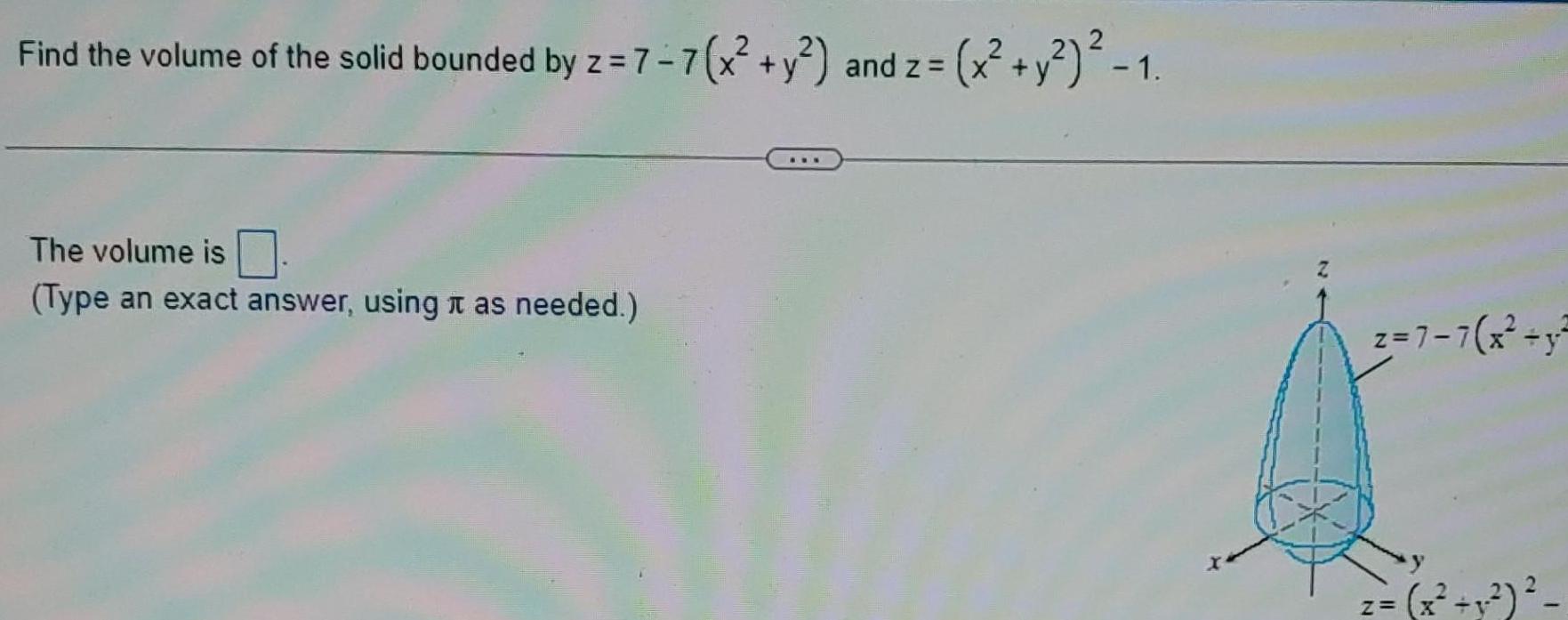
Calculus
Definite IntegralsFind the volume of the solid bounded by z 7 7 x y and z 2 The volume is Type an exact answer using as needed x y 1 z 7 7 x y z x

Calculus
Definite IntegralsIn each part determine all values of p for which the integral is improper Enter in interval notation or none if there are no relevant values of p dx 0 dat 0 XP p values that make integral improper dx x p p values that make integral improper b c S dr

Calculus
Definite IntegralsTherefore the anti derivative of Question 4 Answer The anti derivative of It is known that d ax b 30 ax b 1 d ar b 30 de x b x b Therefore the anti derivative of Question 5 sin 2x 4e Answer The anti derivative of sin 2x 46 It is known that Class XII de Question 6 is the function of x whose derivative is Answer 4 fe de fide sin 2x 4e Therefore the anti derivative of sin 2x 4e is is the function of x whose derivative is Page 2 of 216 Chapter 7 Integrals of sin 2x 40 con 2x is Maths

Calculus
Definite IntegralsUse a calculator to evaluate the trigonometric function Round your answer to four decimal places Be sure the calculator is in the correct moc sin 330

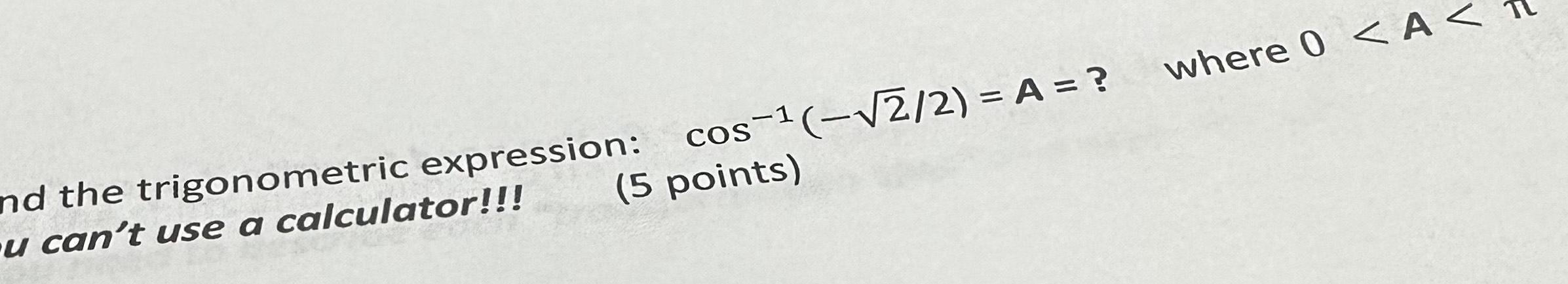
Calculus
Definite Integrals5 points and the trigonometric expression cos 2 2 A u can t use a calculator where 0 A F
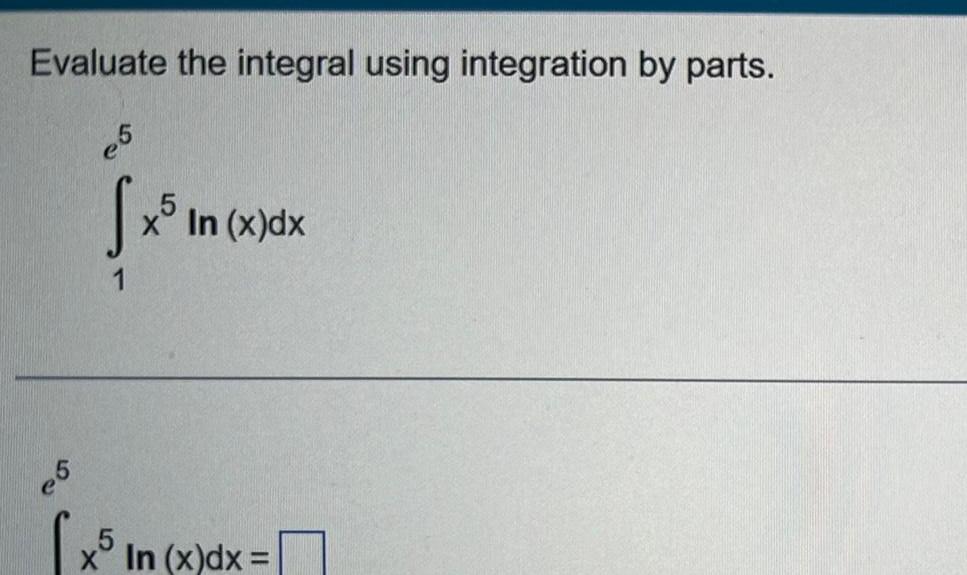
Calculus
Definite IntegralsEvaluate the integral using integration by parts e5 S x In x dx 5 x5 In x In x dx

Calculus
Definite Integrals1 4 7 10 12 6 16 x 3sinx e C 18 tan x sec x C 440 S 4 cos cos x C 12 cos2x ax b 3a 14 20 2 tan x x 3 sec x C 22 A 17 log x 2x C MATHEMATICS 2 c x 4 x 8 C 1 m log x 1 m 2 C 5 C 2 5 9 1 15 sin 3x ax 8 at by a C 9 3x C 18 3 ax b C 7 x 2 x 2 C 3a 6 EXERCISE 7 2 4a 1 4 17 19 tan x x C 21 C 2 ax b C Rationalised 2023 24 logi x C 3 log 1 log x C cos cos 2 a ONCERT not to be republished 10 log19 4x 1 C 16 10 2log x 1 C 1 18 2 3x pe 19 log e e C

Calculus
Definite IntegralsE be the event at least two heads appear and F be the event first coin shows tail Then and Therefore and 1 Since the coins are fair we can assign the probability to each sample point Let Also with or E HHH HHT HTH THH F THH THT TTH TTT P E P HHH P HHT P HTH P THH Thus 1 1 111 Why 88 882 P F P THH P THT P TTH P TTT 408 11111 8 8 8 8 2 P EF P THH Now suppose we are given that the first coin shows tail i e F occurs then what is the probability of occurrence of E With the information of occurrence of F we are sure that the cases in which first coin does not result into a tail should not be considered while finding the probability of E This information reduces our sample space from the set S to its subset F for the event E In other words the additional information really amounts to telling us that the situation may be considered as being that of a new random experiment for which the sample space consists of all those outcomes only which are favourable to the occurrence of the event F Now the sample point of F which is favourable to event E is THH 1 Thus Probability of E considering F as the sample space 4 EnF THH 1 Probability of E given that the event F has occurred 4 This probability of the event E is called the conditional probability of E given that F has already occurred and is denoted by P EIF P EIF MATHEMATICS Note that the elements of F which favour the event E are the common elements of E and F i e the sample points of En F RT 1 P EIF Thus we can also write the conditional probability of E given that F has occurred as Number of elementary events favourable to EnF Number of elementary events which are favourable to F n EF n F Rationalised 2023 24 blished Dividing the numerator and the denominator by total number of elementary events of the sample space we see that P EIF can also be written as n EnF n S n F n S Note that 1 is valid only when P F 0 i e F Why P EIF P EF P F hed 1

Calculus
Definite Integrals1 1 4 Composition of Functions 1 Letf A B and g B C be two functions Then the composition of f and g denoted by g of is defined as the function g of AC given by go f x g y xe A ii Iff A B and g BC are one one then g of A C is also one one iii Iff A B and g BC are onto then g of AC is also onto However converse of above stated results ii and iii need not be true Moreover we have the following results in this direction iv Letf A B and g BC be the given functions such that g of Then fis one one v Letf A B and g BC be the given functions such that g is onto ER 1 1 5 Invertible Function 1 A function f X Y is defined to be invertible if there exists a function g Y X such that g of 1 and fog 1 The function g is called the inverse of fand is denoted by f ii A function f X Y is invertible if and only if f is a bijective function blated one one is onto Then i If f X Y g Y Z and h Z S are functions then ho gof hog of iv Let f X Y and g Y Z be two invertible functions Then g of is also invertible with gof fog 1 1 6 Binary Operations i A binary operation on a set A is a function AxA A We denote a b by a b ii A binary operation on the set X is called commutative if a b ba for every a be X iii A binary operation A x AA is said to be associative if a b c a b c for every a b c e A iv Given a binary operation AxAA an elemente e A if it exists is called identity for the operation if ae a e a ya A 1 2 Solved Examples Short Answer S A Example 1 Let A 0 1 2 3 and define a relation R on A as follows R 0 0 0 1 0 3 1 0 1 1 2 2 3 0 3 3 Is R reflexive symmetric transitive RELATIONS AND FUNCTIONS 3 v Given a binary operation A x AA with the identity element e in A an element a A is said to be invertible with respect to the operation if there exists an element b in A such that a b e ba and b is called the inverse of a and is denoted by a Solution R is reflexive and symmetric but not transitive since for 1 0 3 e R whereas 1 3 Example 2 For the set A 20 04 2018 R and R 11 2 3 define a relation R in the set A as follows

Calculus
Definite Integralsn F Dividing the numerator and the denominator by total number of elementary events of the sample space we see that P EIF can also be written as P EIF Also Note that 1 is valid only when P F 0 i e F Why Thus we can define the conditional probability as follows Definition 1 If E and F are two events associated with random experiment the conditional probability of the event E given that F has occurred i e P EIF is given by P EIF We have n EF n S n F n S P SIF 13 2 1 Properties of conditional probability Let E and F be events of a sample space S of an experiment then we have Property 1 P SIF P FIF 1 We know that P EF P F P FF P F P AUB IF P SOF P F P F P F provided P F 0 P FIF Thus P SIF P FIF 1 Property 2 If A and B are any two events of a sample space S and F is an event of S such that P F 0 then P AUB IF P A F P BIF P AB IF Rationalised 2023 24 P F 1 P F In particular if A and B are disjoint events then P AUB IF P A F P BIF P AUB FI P F same sample space of a Property 3 P EIF 1 P EIF From Property 1 we know that P SIF 1 P EEF 1 pride you P AF U BF P F by distributive law of union of sets over intersection P AF P BOF P AOB OF P F When A and B are disjoint events then P AB IF 0 P AB F P A F P BIF PROBABILITY 409 P AF P BF P AB FJ P F P F P F P A F P BIF P AB IF since SEVE

Calculus
Definite Integrals1 4 ax b 3a 7 10 log x 2x C 2 12 14 16 x 3sin x e C 18 tan x sec x C 6 440 20 2 tan x 3 sec x C 22 A C 8 11 4 cos cos x C 5 12 14 17 2 5 MATHEMATICS 8 log x 1 m C ONCERT not to be republished sin 3x 3 9 C 15 2 cx 4a x 4 x 8 C x c 3 EXERCISE 7 2 ax b C 7 x 2 x 2 C 3a 6 2 logixl C 3 log 1 logx C 9 1 cos 2 ax b C Rationalised 2023 24 x x 1 C 17 3 19 tan x x C 21 C 18 C 4 3cos x 10 13 log19 4x 1 C 16 10 2log x 1 C 1 18 2 3x 19 log e e C Ble te 9 C
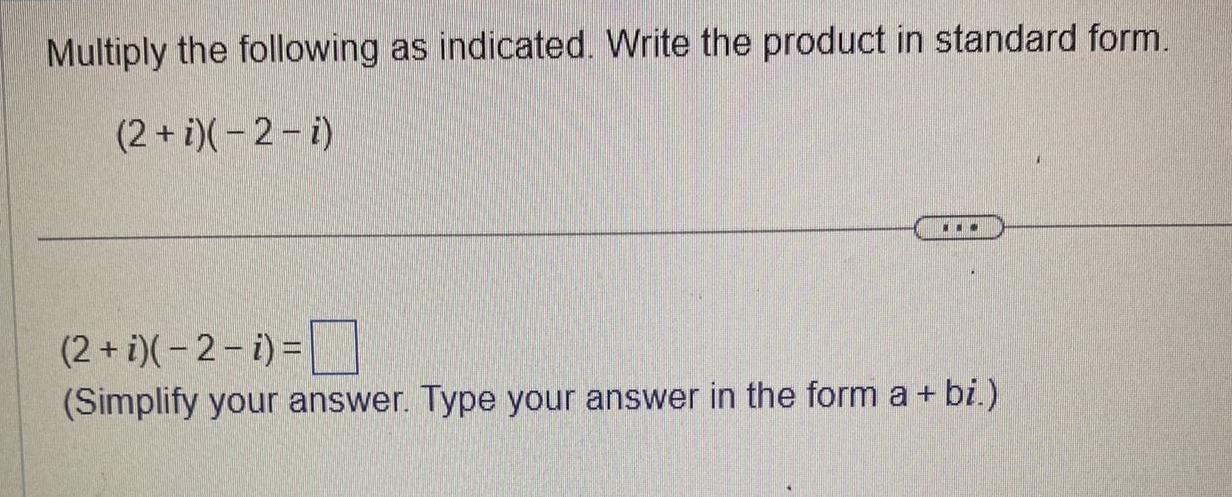
Calculus
Definite IntegralsMultiply the following as indicated Write the product in standard form 2 i 2 i 2 i 2 i Simplify your answer Type your answer in the form a bi

Calculus
Definite IntegralsThe sun is 22 above the horizon Find the length of a shadow cast by a park statue that is 12 feet tall Round your answer to one decimal place ft
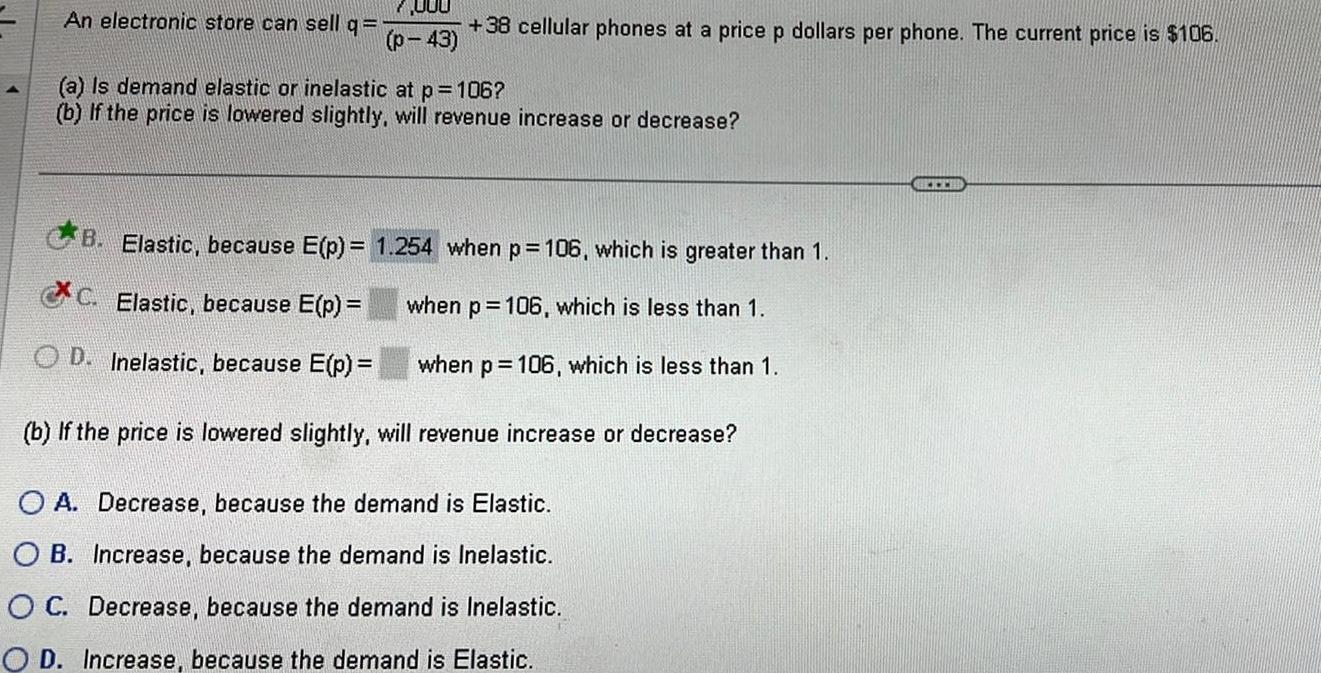
Calculus
Definite Integrals000 p 43 An electronic store can sell q 1 38 cellular phones at a price p dollars per phone The current price is 106 a Is demand elastic or inelastic at p 106 b If the price is lowered slightly will revenue increase or decrease B Elastic because E p C Elastic because E p OD Inelastic because E p b If the price is lowered slightly will revenue increase or decrease O A Decrease because the demand is Elastic OB Increase because the demand is Inelastic OC Decrease because the demand is Inelastic OD Increase because the demand is Elastic 1 254 when p 106 which is greater than 1 when p 106 which is less than 1 when p 106 which is less than 1 www
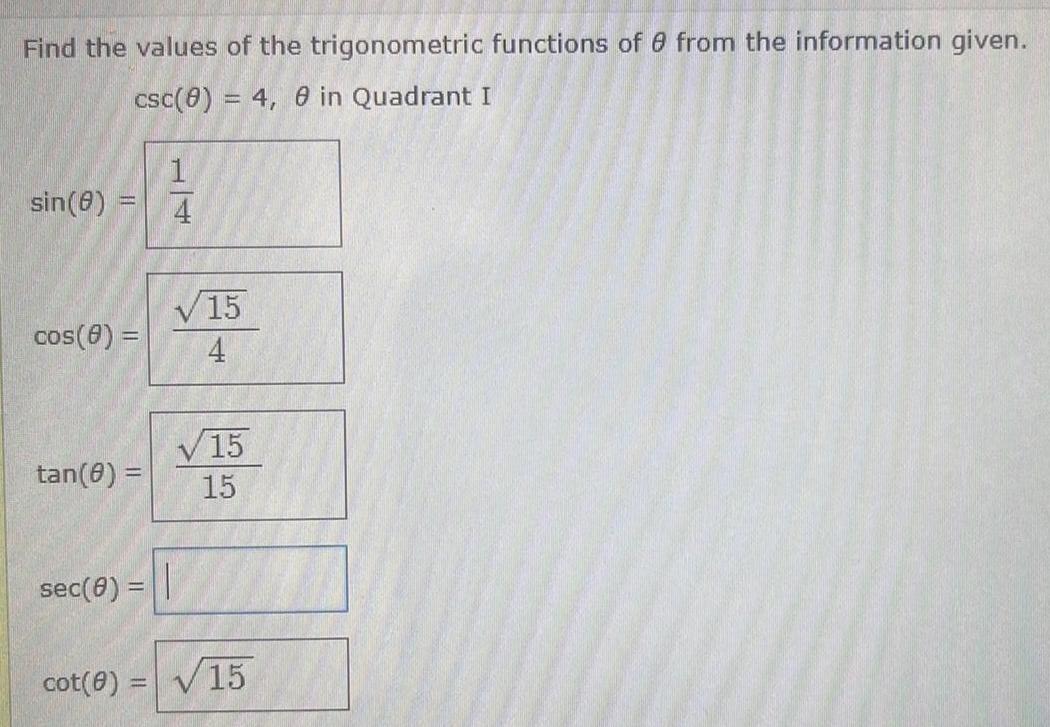
Calculus
Definite IntegralsFind the values of the trigonometric functions of 8 from the information given csc 0 4 8 in Quadrant I sin 8 cos 8 tan 8 sec 0 cot 0 1 4 15 4 15 15 15

Calculus
Definite Integralsopen interval I gives rise to the succession of derivatives 9 dX d x d X dt dt dt Now a differential equation in the function X t is therefore an equation of the type X MATHEMATICS F1 X du x X dX d X dt d 2 du x x 1 i n Such an equation is said to be an ordinary differential equation Thus an ordinary differential equation is a differential equation in which the constituent function X X t is a function of a single real variable Tim We often use the acronym ODE in place of the full term ordinary differential equation j1 i j n D u de X dik II On the other hand there are differential equations in a function u xu x of a real multivariable x x x x which ranges in an open subset of R Such a function u u x gives rise to mixed partial derivatives 0 Fx u 1 GJEJ 65 for various multi indices a a a with o Zi 0 1 2 the mixed partial derivative D u having the order a o 0 Now a differential equation in such a function u ux of a multi variable x x ranging in an open subset of R is an equation of the type du d u Du o m 0 2 x x dx its order being m Equation 2 is said to be a partial differential equation in u x because it involves the mixed partial derivatives of u We use the acronym PDE for this type of differential equations There is more about the setting of a differential equation In a mathematical problem a differential equation is accompanied by auxiliary data A solution of a differential equation is required to satisfy this auxiliary data To be more specific we are given a subset of the domain of a prospective solution and some of its derivatives of the solution at the points of this subset

Calculus
Definite IntegralsFind the volume of the region bounded by the coordinate planes the plane x y 5 and the cylinder y 9z 2 25 2 The volume is Type an exact answer using as needed

Calculus
Definite Integralsy cosec x 07 201 restrict the domain of secant function to 0 x 0 y see x 0 1 the domain of y secx is the set R x x 2n 1 COS X n Z and range is the set R 1 1 It means that sec secant function assumes all real values except 1 1 and is not defined for odd multiples of 3 If we Y y cosec x Rationalised 2023 24 Fig 2 3 ii then it is one one and onto with its range as the set R 1 1 Actually secant function restricted to any of the 3x intervals 1 0 0 n 2n etc is bijective and its range 3x is R 1 1 Thus sec can be defined as a function whose domain is R 1 1 and range could be any of the intervals 7 0 0 n 2n etc Corresponding to each of these intervals we get different branches of the function sec The branch with range 0 is called the principal value branch of the function sec We thus have R R 1 1 0 x 1 A 2 INVERSE TRIGONOMETRIC FUNCTIONS 23 see 161 The graphs of the functions y sec x and y sec x are given in Fig 2 4 1 ii CERT reptableted y sec x

Calculus
Definite Integrals1 log 3 log x 1 5log x 2 4log x 3 C 4 log x 1 2log x 2 log x 3 C 5 4log x 2 2log x 1 C 8 10 11 12 29 50 5 3 x 2 C 1 x 2 3 x 1 log x 1 log x 1 5 444 20 22 14 3log x 2 C 7 x 2 16 log n 13 log x 1 log 1 x tan x C 18 x 3 log x 1 log x 2 log x 2 C log x log x 1 C x 4 22 B 1 H tan C X 3 MATHEMATICS 3tan 2 1 x cos x sin x C 6 3 e x 2x 2 C log2r C 6 15 log 19 17 log log 4 x 1 x 3 21 Rationalised 2023 24 2 sin x 1 siny blished 23 A EXERCISE 7 6 6 x 1 C 10g c 2 cos3x sin 3x C 4 log x tan x C log x C pe

Calculus
Definite Integralscollinear Solution Direction ratios of line joining A and B are 1 2 2 3 3 4ie 1 5 7 The direction ratios of line joining B and Care 3 1 8 2 11 3 ie 2 10 14 It is clear that direction ratios of AB and BC are proportional hence AB is parallel to BC But point B is common to both AB and BC Therefore A collinear points B C are EXERCISE 11 1 1 Ifa line makes angles 90 135 45 with the x y axes respectively find its direction cosines 2 Find the direction cosines of a line which makes equal angles with the coordinate axes 3 If a line has the direction ratios 18 12 4 then what are its direction cosines 4 Show that the points 2 3 4 1 2 1 5 8 7 are collinear 5 Find the direction cosines of the sides of the triangle whose vertices are 3 5 4 1 1 2 and 5 5 2 11 3 Equation of a Line in Space We have studied equation of lines in two dimensions in Class XI we shall now study the vector and cartesian equations of a line in space A line is uniquely determined if 1 it passes through a given point and has given direction or i it passes through two given points 11 3 1 Equation of a line through a given point and parallel to a given vector h Let a be the position vector of the given point A with respect to the origin O of the rectangular coordinate system Let be the line which passes through the point A and is parallel to a given vector b Let 7 be the position vector of an arbitrary point P on the line Fig 11 3 382 MATHEMATICS Then AP is parallel to the vector b i e AP b where is some real number But i e Rationalised 2023 24 AP OP 0A 2b 7 a Conversely for each value of the parameter A this equation gives the position vector of a point P on the line Hence the vector equation of the line is given by F a b and a ishd A P Fig 11 3 Pl Y 1 Remark If h ai b ck then a b c are direction ratios of the line and conversely if a b c are direction ratios of a line then b ai bj ck will parallel to the line Here b should not be confused with bl Derivation of cartesian form from vector form Let the coordinates of the given point A be x y z the direction ratios of the line be a b Consider the ates of any point Pbe x y z Then x i y j z k 7 xi y zk b al b ck Substituting these values in 1 and equating the coefficients of 1 and k we get x x a y y b z z kc 2 These are parametric cautions of the line Fliminating the parameter from 2
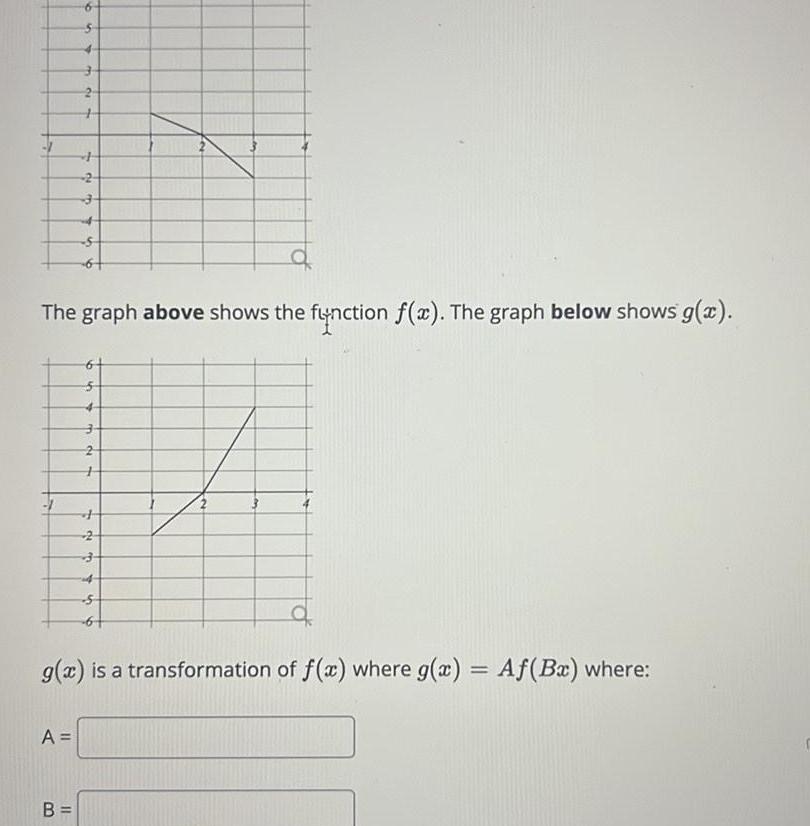
Calculus
Definite IntegralsThe graph above shows the function f x The graph below shows g x A 2 3 B 11 5 g x is a transformation of f x where g x Af Bx where 3 4
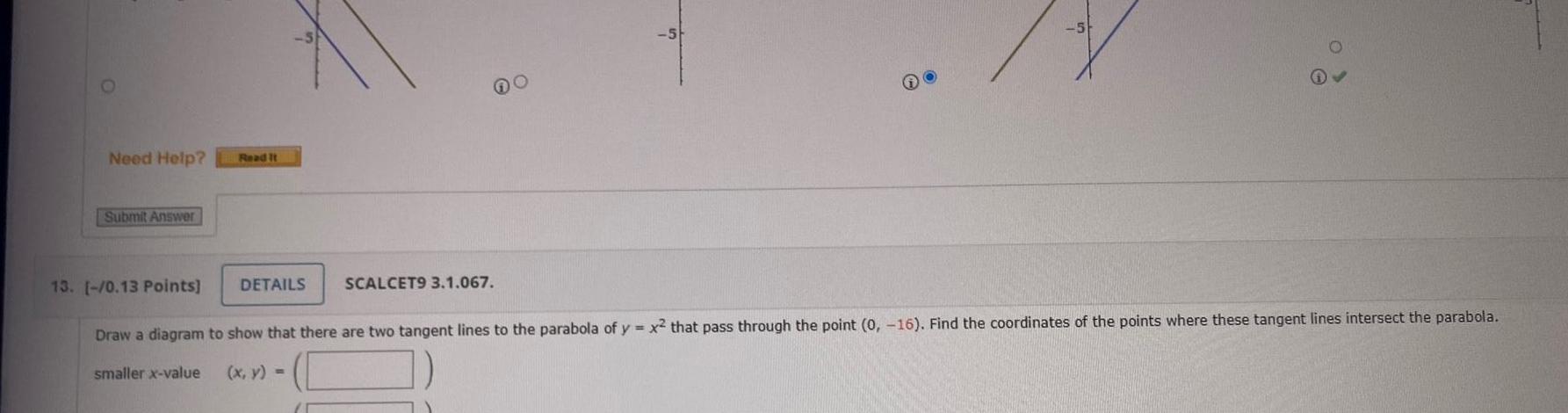
Calculus
Definite IntegralsNeed Help Submit Answer Read It DETAILS SCALCET9 3 1 067 13 0 13 Points Draw a diagram to show that there are two tangent lines to the parabola of y x that pass through the point 0 16 Find the coordinates of the points where these tangent lines intersect the parabola smaller x value x y

Calculus
Definite IntegralsFind the interval of convergence for the given power series The series is convergent from x to x left end included Y N right end included Y N 12 1 n x 11 10 n

Calculus
Definite Integrals3 log 5 3 2 2 11 x tan 3x 1 c C 13 log x 2 x 3x 2 C 15 log x a b x a x b C 2 6 4x 5 22 tan 2x C 6 7 1 log x 1 C 8 log x x a C 9 log tanx tan x 4 C 10 log x 1 2x 2 C 16 2 2x x 3 C 18 log 3x 2x 1 19 6 x 9x 20 6 log 6 9 12 sin 2 5x 3 0 in c 21 x 2x 3 log x 1 2x 3 C 1 x 1 x 3 9x 20 C log x 2x 5 7 log x 1 6 C C 1 210g x 1 C you to be rept lished

Calculus
Definite Integralsdx dt dy dt 2x 1 1 2 xy 3y 1 3 2xy a Find the value for each of the six parameters r1 72 K K2 01 02 b Perform nullcline analysis draw all nullclines draw the arrows in each section and across each nullclines indicating if each population increases or decreases find and label each equilibrium use this sketch to label each equilibria as stable or unstable if possible c Determine the stability of the equilibrium at coexistence neither population is extinct by linearizing around that equilibrium Find the Jacobian the matrix of partial derivatives Evaluate the Jacobian at the equilibria in question Either calculate the eigenvalues of this matrix OR use the trace determinant

Calculus
Definite IntegralsFind the volume of the solid whose base is the region in the xy plane that is bounded by the parabola y 4 x and the line y 3x while the top of the solid is bounded by the plane z x 8 The volume is units Type an integer or a simplified fraction

Calculus
Definite IntegralsFind the volume of the region bounded above by the paraboloid z x y and below by the triangle enclosed by the x y lines y x x 0 and x y 2 in the xy plane The volume under the paraboloid is Type a simplified fraction