Differential equations Questions and Answers

Calculus
Differential equationsSolve the following equation.
x^-2 - 4x^-1 - 5 = 0
Larger x =
Smaller x =

Calculus
Differential equationsFind the relative maximum and minimum values.
f(x,y) = e^(8x² + 5y² + 6)
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative maximum value of f(x,y) = at (x,y) =
B. The function has no relative maximum value.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative minimum value of f(x,y) = at (x,y) =
B. The function has no relative minimum value.
Calculus
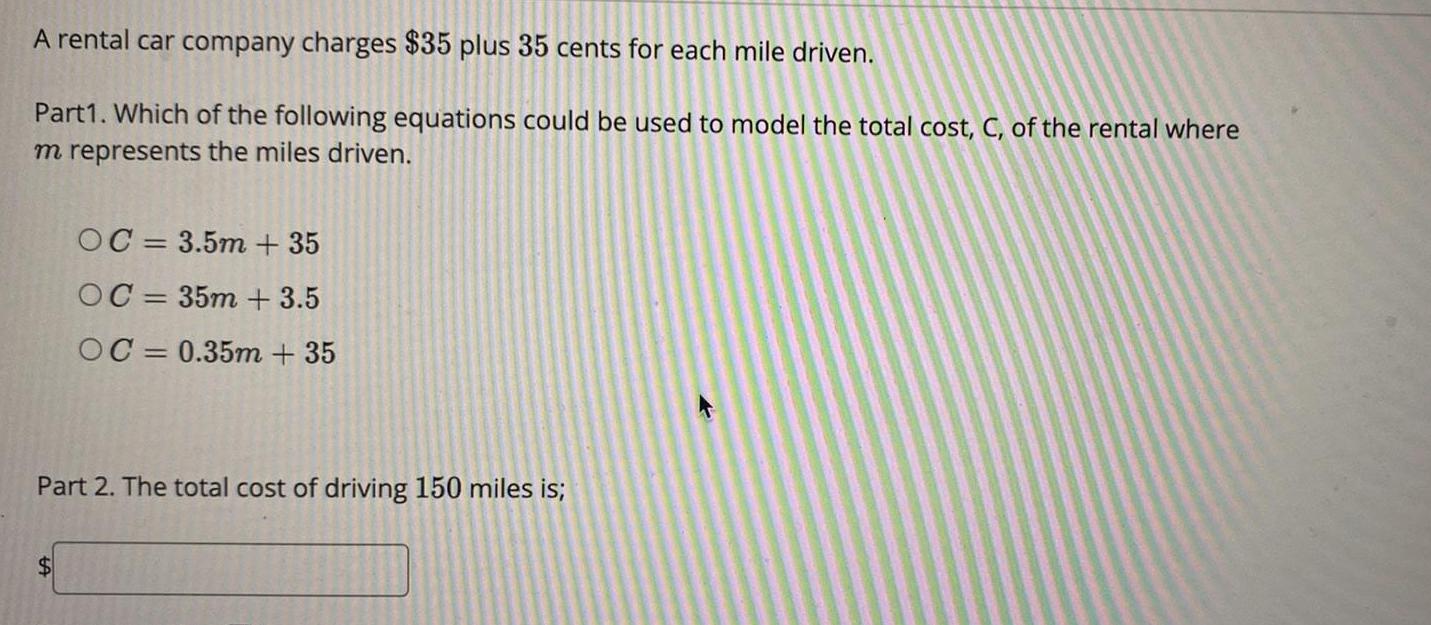
Differential equationsA rental car company charges $35 plus 35 cents for each mile driven.
Part1. Which of the following equations could be used to model the total cost, C, of the rental where
m represents the miles driven.
C= 3.5m + 35
C= 35m + 3.5
C= 0.35m + 35
Part 2. The total cost of driving 150 miles is;
Calculus
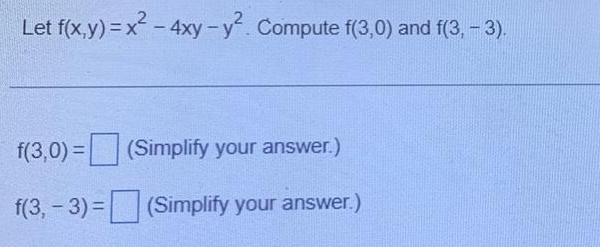
Differential equationsLet f(x,y)=x² - 4xy-y. Compute f(3,0) and f(3,-3).
f(3,0)= (Simplify your answer.)
f(3,-3)= (Simplify your answer.)
Calculus
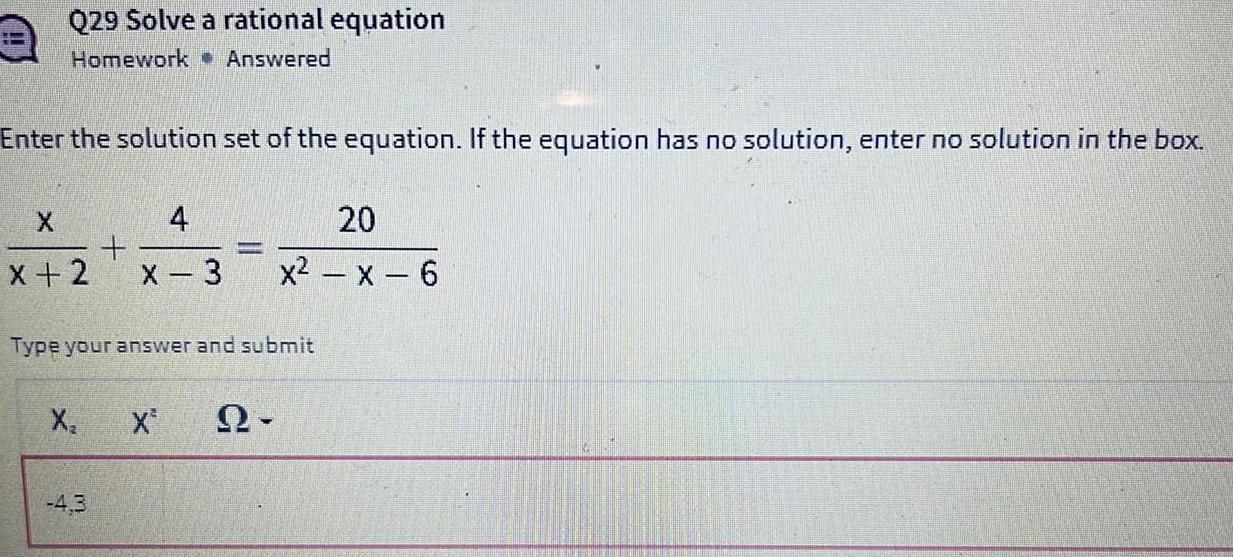
Differential equationsEnter the solution set of the equation. If the equation has no solution, enter no solution in the box.
x x +2 + 4 x - 3 = 20 x2 - x - 6
Type your answer and submit
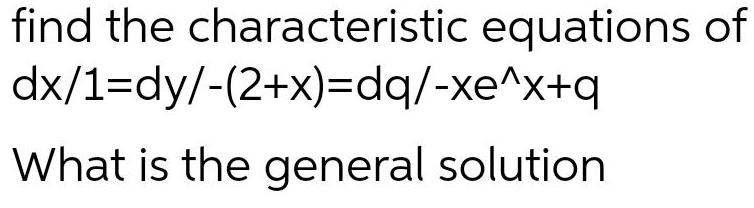
Calculus
Differential equationsfind the characteristic equations of dx/1=dy/-(2+x)=dq/-xe^x+q
What is the general solution

Calculus
Differential equationsOn which interval is the IVP (z cos x)y' + 2y = x+1, y(-5) = 2 guaranteed to have a unique solution?
(-∞,∞)
(-∞,∞)
(-5,∞)
(-5,0)
(-π,π)
(0,π 2)
(-π 2,π 2)
(0, π 2)
(-π 2,0)
(-2π,-3π 2)
(-5π 2,-3π 2)
(-5π 2,5π 2)
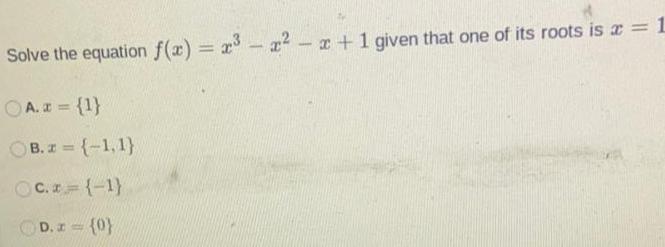
Calculus
Differential equationsSolve the equation f(x) = x³ = x²-x+1 given that one of its roots is a = 1
A. x = {1}
B. z={-1,1}
c.z={-1}
D. z = {0}

Calculus
Differential equationsMark dropped a phone from his apartment balcony. In an apartment below, Madelyn noticed the phone pass by her 2.4-meter tall window in 0.026 seconds. From how high above the top of Madelyn's window did Mark drop the phone? Round the solution to the nearest tenth, if necessary. motors
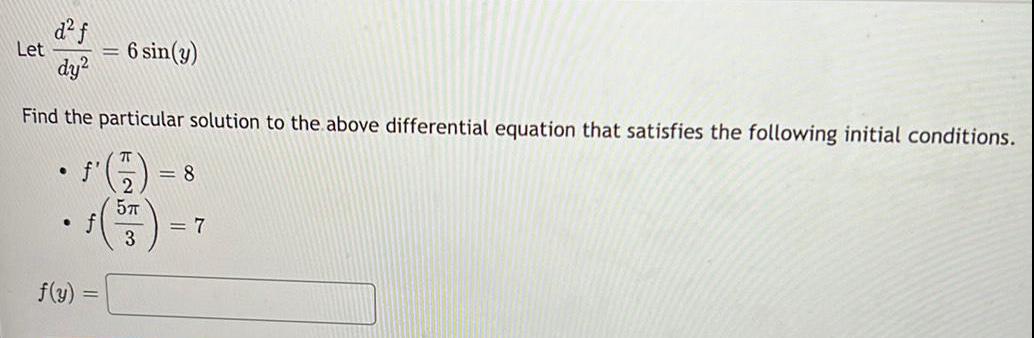
Calculus
Differential equationsLet d²f dy² = 6 sin (y)
Find the particular solution to the above differential equation that satisfies the following initial conditions.
f'(π 2) = 8
f(5π 3) = 7

Calculus
Differential equationsLet f''(x) = 1 2x3 2
Find the particular solution to the above differential equation that satisfies the following initial condition.
f has a horizontal tangent line at (1, 2).
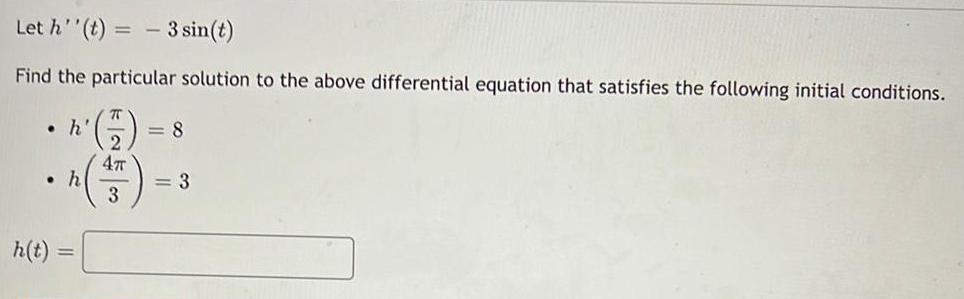
Calculus
Differential equationsLet h''(t) = -3 sin(t)
Find the particular solution to the above differential equation that satisfies the following initial conditions.
h'(π/2)=8
h(4π/3)=3
h(t)=
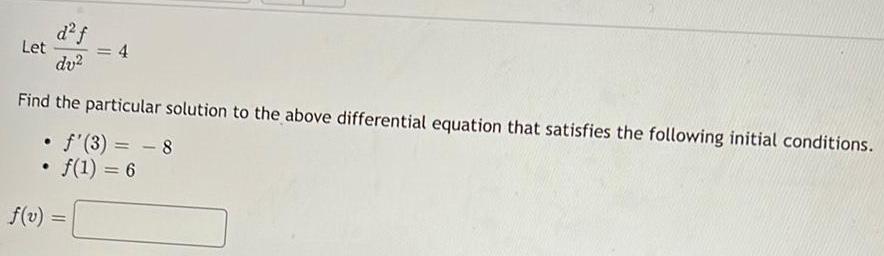
Calculus
Differential equationsLet d² f/dv²=4
Find the particular solution to the above differential equation that satisfies the following initial conditions.
• f'(3) = -8
f(1) = 6
f(v) =

Calculus
Differential equationsLet d² f/dz²=e^- 4z
Find the particular solution to the above differential equation that satisfies the following initial conditions.
f'(0) = 8
f(0) = 7
f(z) =

Calculus
Differential equationsLet dg/dy=3e^y
Find the particular solution to the above differential equation that satisfies the following initial condition.
• g(-3) = 2
g(y)=

Calculus
Differential equationsLet h''(x) = 36x + 16
Find the particular solution to the above differential equation that satisfies the following initial conditions.
• h'(0) = 2
• h(- 6) = -1
h(x)=

Calculus
Differential equationsLet d^2h/dt²=30t
Find the particular solution to the above differential equation that satisfies the following initial conditions.
h'(0) = 7
h(9) = -5
h(t)=

Calculus
Differential equationsLet dh/dx=-6/1+x^2
Find the particular solution to the above differential equation that satisfies the following initial condition.
• h(1) = -3
h(x)

Calculus
Differential equationsFind the area of the region under the graph of the following function.
f(x) = 2xe-x from x = 4 to x = 7
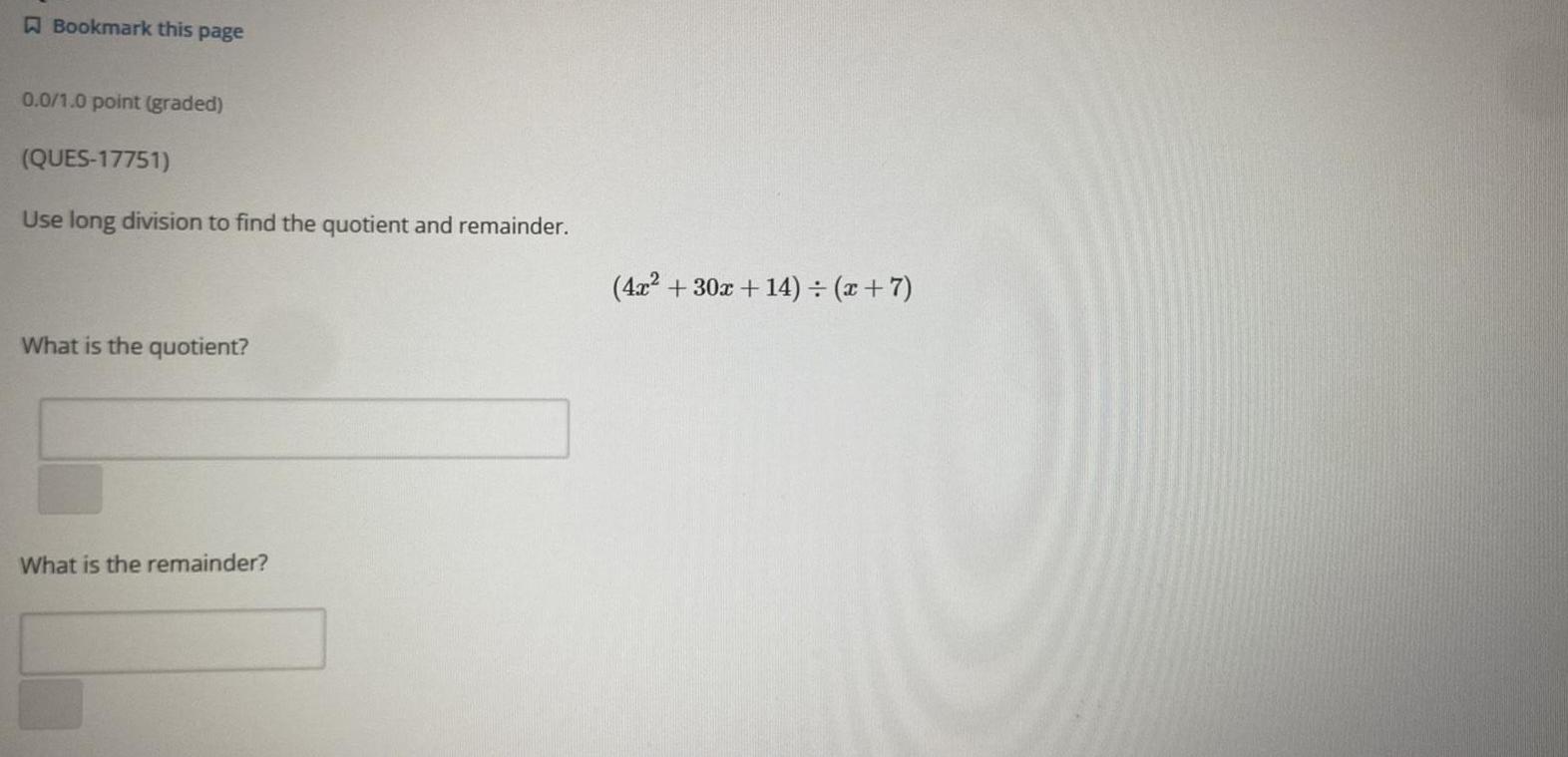
Calculus
Differential equationsUse long division to find the quotient and remainder.
(4x² + 30x+14) / (x + 7)
What is the quotient?
What is the remainder?

Calculus
Differential equationsIf a = 20 and c = = 28, find the missing sides and angles in the right triangle, where a is the side opposite of angle A, b is the side opposite of angle B and c is opposite of the right angle, angle C.
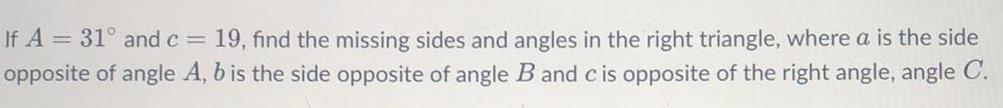
Calculus
Differential equationsIf A = 31° and c = 19, find the missing sides and angles in the right triangle, where a is the side opposite of angle A, b is the side opposite of angle B and c is opposite of the right angle, angle C.
Calculus
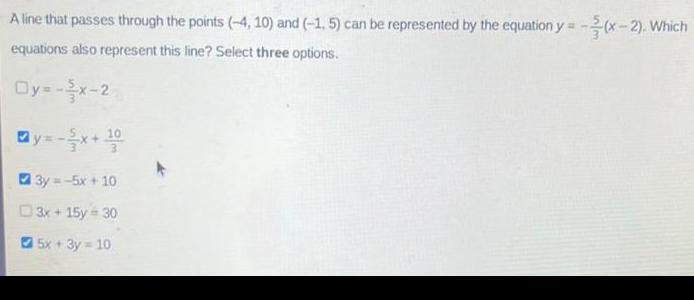
Differential equationsA line that passes through the points (-4, 10) and (-1, 5) can be represented by the equation y=-5 3(x-2). Which equations also represent this line? Select three options.
y=-5 3x-2
y=-5 3x+10 3
3y = -5x + 10
3x + 15y = 30
5x + 3y = 10
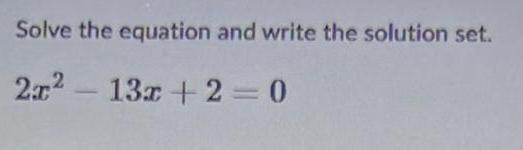

Calculus
Differential equationsFind (gof)(x) for the given functions. Simplify the expression. Do not enter any spaces in the answer.
f(x) = 6x - 1, g(x) = 5x + 2

Calculus
Differential equationsGiven the following function, determine the interval for the principal cycle. Then for the principal cycle, determine the equations of the vertical asymptotes, the coordinates of the center point, and the coordinates of the halfway points. Sketch the graph
y = tan (x - π 3)
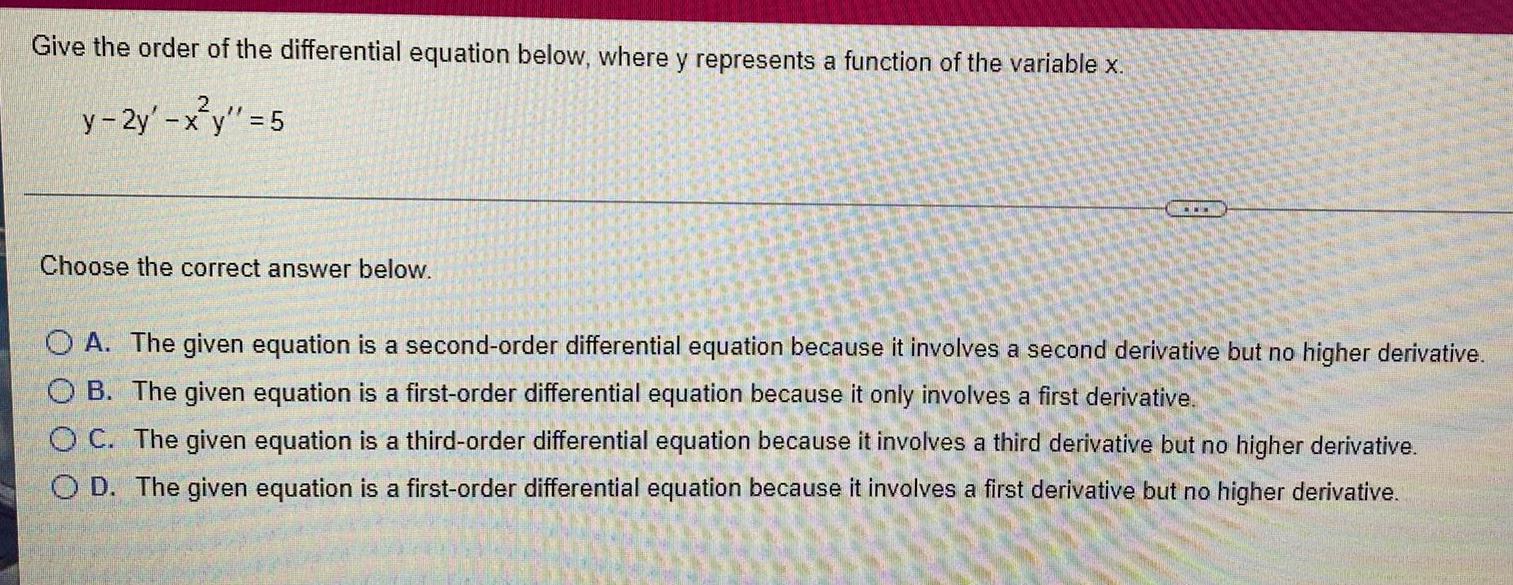
Calculus
Differential equationsGive the order of the differential equation below, where y represents a function of the variable x.
y-2y'-x²y" = 5
Choose the correct answer below.
A. The given equation is a second-order differential equation because it involves a second derivative but no higher derivative.
B. The given equation is a first-order differential equation because it only involves a first derivative.
C. The given equation is a third-order differential equation because it involves a third derivative but no higher derivative.
D. The given equation is a first-order differential equation because it involves a first derivative but no higher derivative.
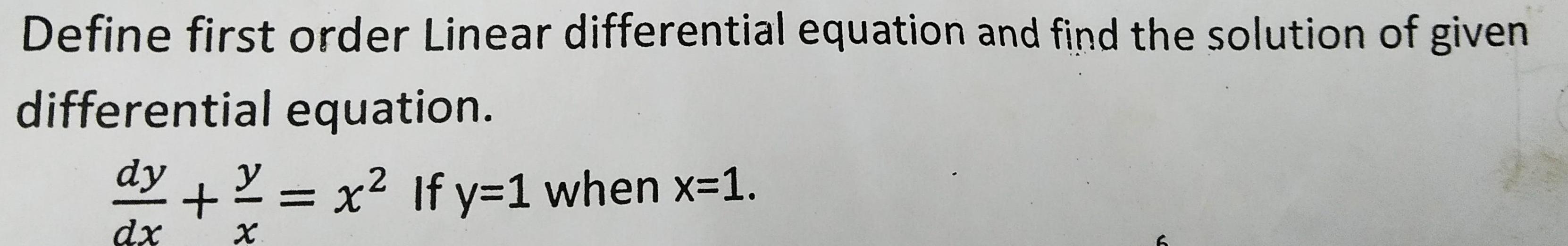
Calculus
Differential equationsDefine first order Linear differential equation and find the solution of given
differential equation.
dy/dx + y/x = x² If y=1 when x=1.

Calculus
Differential equationsUse ordinary division of polynomials to find the quotient and remainder.
(b2-3b-28)÷(b + 2)
Choose the correct quotient.
A. b-28, R 11
B. b-7
C. b-4
D. b-5, R (-18)
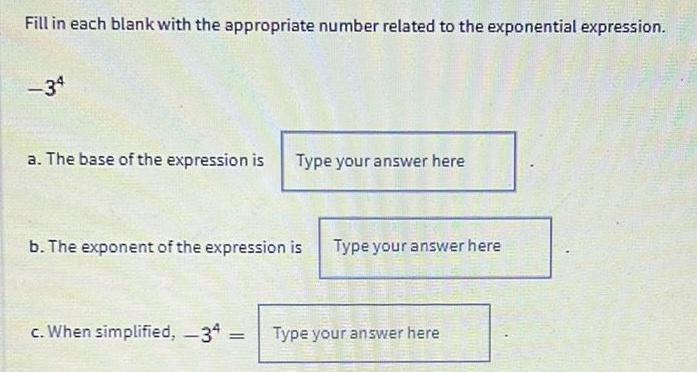
Calculus
Differential equationsFill in each blank with the appropriate number related to the exponential expression.
-34
a. The base of the expression is Type your answer here
b. The exponent of the expression is Type your answer here
c. When simplified, -34 = Type your answer here
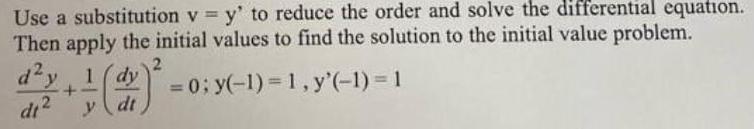
Calculus
Differential equationsUse a substitution v=y' to reduce the order and solve the differential equation.
Then apply the initial values to find the solution to the initial value problem.
d²y /dt²+ 1/y (dy/dx)^2= 0; y(-1)= 1, y'(-1)=1
Calculus
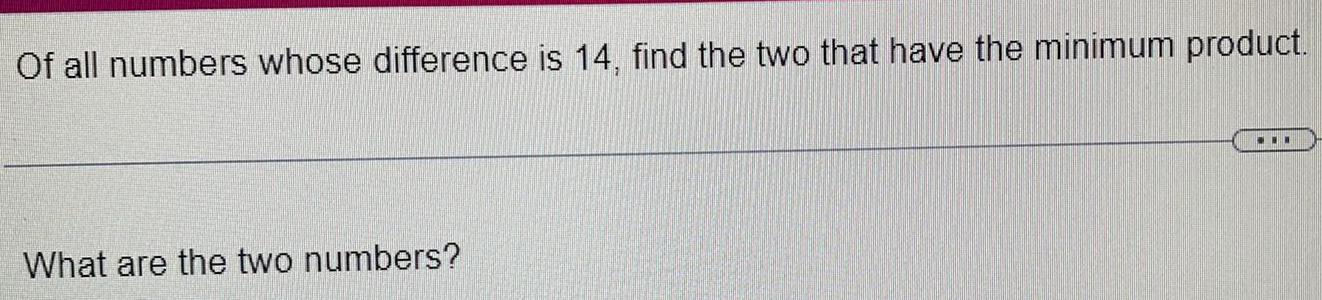
Differential equationsOf all numbers whose difference is 14, find the two that have the minimum product.
What are the two numbers?
Calculus
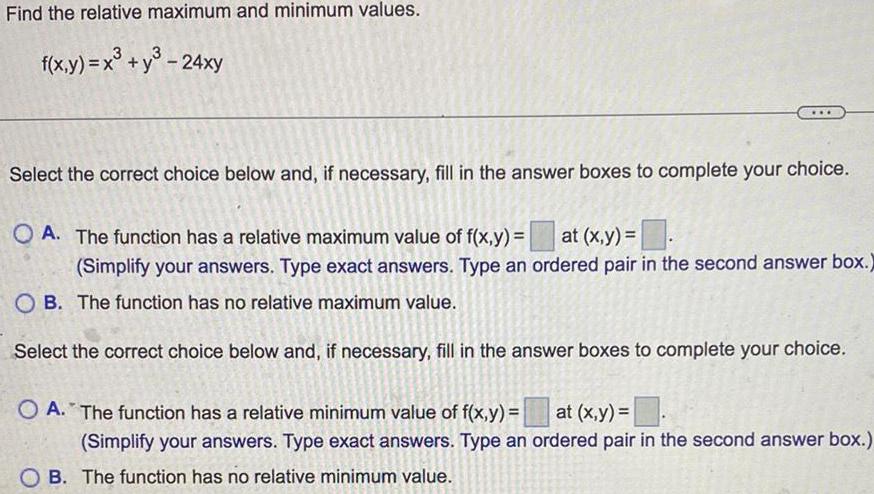
Differential equationsFind the relative maximum and minimum values.
f(x,y) = x³ +y³ - 24xy
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative maximum value of f(x,y) = at (x,y) =
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative maximum value.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative minimum value of f(x,y) = at (x,y) =
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative minimum value.

Calculus
Differential equationsThe population density of a city is given by P(x,y)= -25x²-20y² + 200x+600y + 180, where x and y are miles from the southwest corner of the city limits and P is the number of people per square mile. Find the maximum population density, and specify where it occurs.
The maximum density is people per square mile at (x,y)=
Calculus
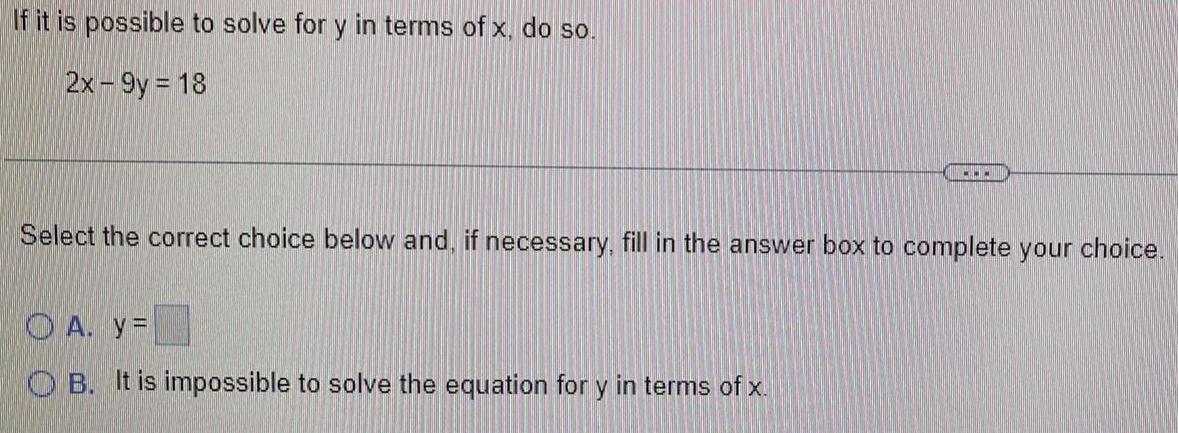
Differential equationsIf it is possible to solve for y in terms of x, do so.
2x - 9y = 18
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. y=
B. It is impossible to solve the equation for y in terms of x.
Calculus
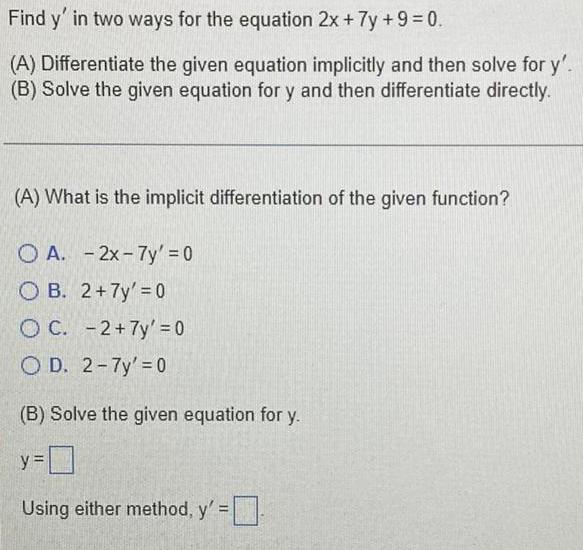
Differential equationsFind y' in two ways for the equation 2x + 7y + 9 = 0.
(A) Differentiate the given equation implicitly and then solve for y'.
(B) Solve the given equation for y and then differentiate directly.
(A) What is the implicit differentiation of the given function?
A. -2x-7y' = 0
B. 2+7y' = 0
C. -2+7y' = 0
D. 2-7y' = 0
(B) Solve the given equation for y.
y=
Using either method, y' =

Calculus
Differential equationsUse the price-demand equation to find the values of p for which demand is elastic and the values for which demand is inelastic. Assume that price and demand are both positive.
x = f(p) = 1936-4p²
The values of p for which demand is elastic are
(Simplify your answer. Type your answer in interval notation. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression.)
The values of p for which demand is inelastic are
(Simplify your answer. Type your answer in interval notation. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression.)
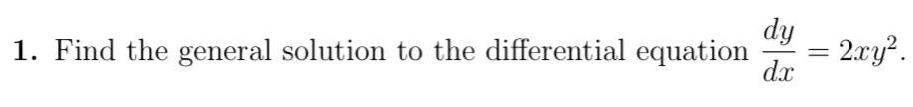
Calculus
Differential equations1. Find the general solution to the differential equation dy/ dx = 2xy².
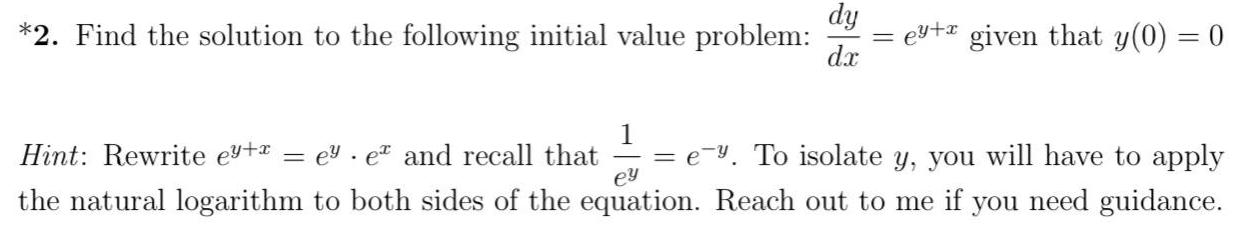
Calculus
Differential equations*2. Find the solution to the following initial value problem: dy/ dx = e^y+x given that y(0) = 0

Calculus
Differential equationsFor the function f(x)=(x-1) 4/5
(a) Find the critical numbers off (if any);
(b) Find the open intervals where the function is increasing or decreasing; and
(c) Apply the First Derivative Test to identify all relative extrema.
Use a graphing utility to confirm your results.
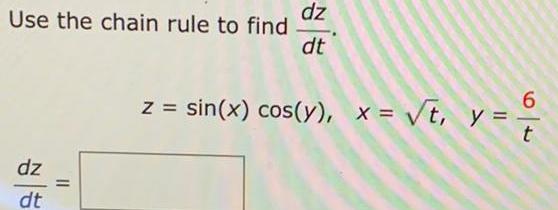
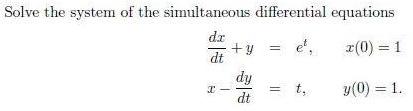
Calculus
Differential equationsSolve the system of the simultaneous differential equations
dx/dt + y = e^t, x(0) = 1
x - dy/dt = t, y(0) = 1

Calculus
Differential equationsNext question A motorcyclist being monitored by radar accelerates at a constant rate from 0 mph (v(0)=0) to 55 mph in 18 sec. How far has the motorcycle traveled after 18 sec? (Hint: Convert seconds to hours.)


Calculus
Differential equationsConsider the following.
x = sin(6t), y = cos(6t), z = 12t, (0, 1, 2π)
Find the equation of the normal plane of the curve at the given point.
Find the equation of the osculating plane of the curve at the given point.
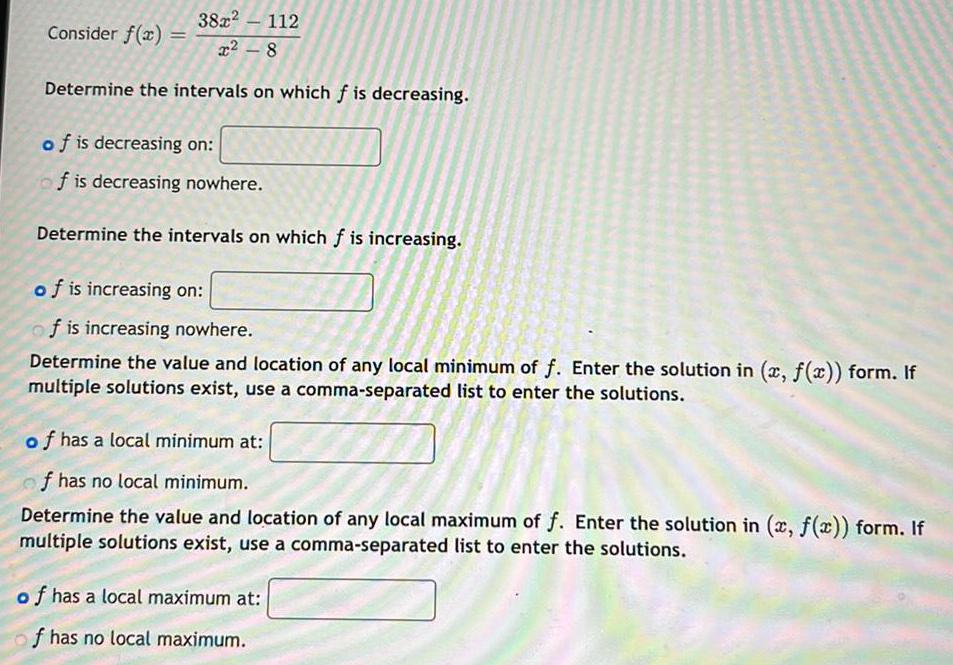
Calculus
Differential equationsConsider f(x) = 38x² -112 / x²-8
Determine the intervals on which f is decreasing.
f is decreasing on:
f is decreasing nowhere.
Determine the intervals on which f is increasing.
f is increasing on:
f is increasing nowhere.
Determine the value and location of any local minimum of f. Enter the solution in (x, f(x)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
f has a local minimum at:
f has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (x, f(x)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
f has a local maximum at:
f has no local maximum.
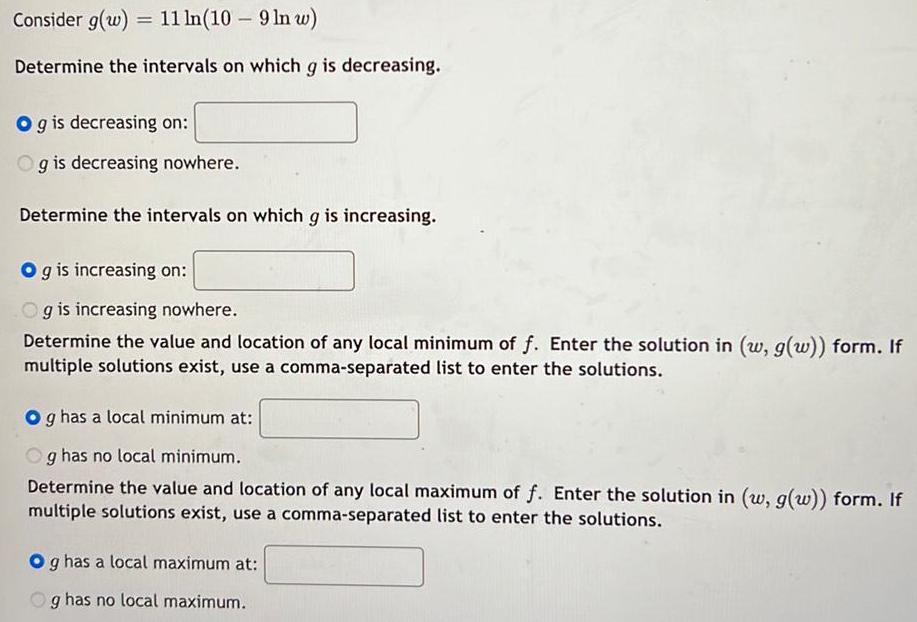
Calculus
Differential equationsConsider g(w) 11 ln(10 - 9 ln w)
=
Determine the intervals on which g is decreasing.
Og is decreasing on:
Og is decreasing nowhere.
Determine the intervals on which g is increasing.
Og is increasing on:
Og is increasing nowhere.
Determine the value and location of any local minimum of f. Enter the solution in (w, g(w)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
Og has a local minimum at:
g has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (w, g(w)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
Og has a local maximum at:
g has no local maximum.

Calculus
Differential equationsAn oceanographer claims that the mean dive duration of a North Atlantic right whale is 11.4 minutes. A random sample of 33 dive durations has a mean of 12.4 minutes and a standard deviation of 2.3
minutes. At x = 0.05 is there enough evidence to reject the oceanographer's claim? Complete parts (a) through (d) below. Assume the population is normally distributed.
Ho:
Ha:
(Type integers or decimals. Do not round.)
The claim is the
hypothesis.
(b) Use technology to find the P-value. Find the standardized test statistic, t.
t =
(Round to two decimal places as needed.)
Obtain the P-value.
P =
(Round to three decimal places as needed.)
(c) Decide whether to reject or fail to reject the null hypothesis.
Ho because the P-value
(d) Interpret the decision in the context of the original claim.
There
enough evidence at the % level of significance to
(Type integers or decimals. Do not round.)
greater than α.
support
reject
the claim that the mean dive duration of a North Atlantic right whale is
minutes.
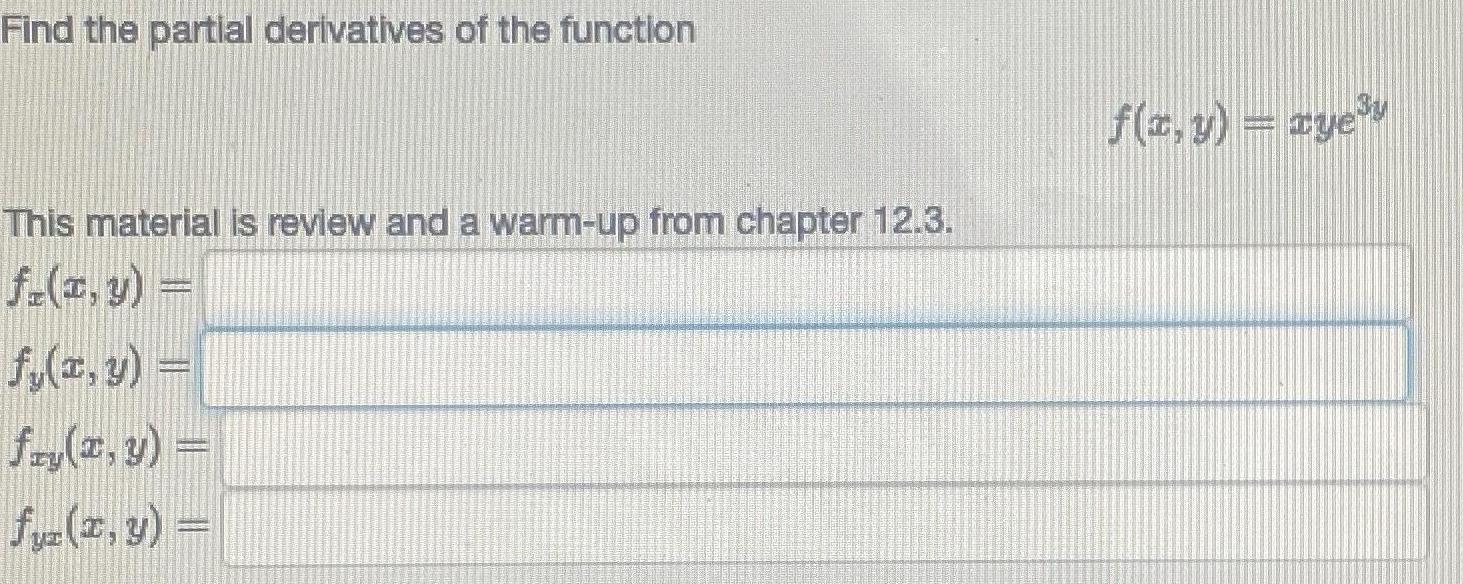
Calculus
Differential equationsFind the partial derivatives of the function
f(x, y) = xye^3y
fx(x, y) =
fy(x, y) =
fxy(x, y) =
fyx(x, y) =

Calculus
Differential equationsGiven the following linear system of ODE:
V₁' = 4y₁+2y₂
V₂' = 10y₁-4y₂
what is the type of the critical point?
the critical point is spiral
the critical point is saddle
the critical point is proper node
the critical point is center
the critical point is improper node