Differential equations Questions and Answers
Calculus
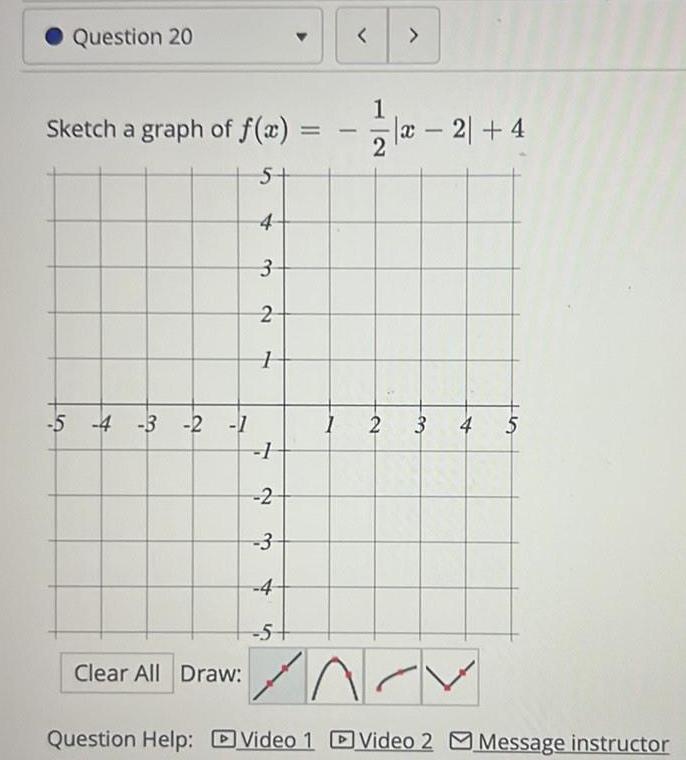
Differential equationsQuestion 20 Sketch a graph of f x 5 4 3 2 1 5 4 3 2 1 1 2 3 4 5 Clear All Draw 1 1 2 2 x2 4 3 4 5 NCY n Question Help Video 1 Video 2 Message instructor
Calculus
Differential equationsSubmit Answer 0 13 Points DETAILS SCALCET9 3 1 074 Find a parabola with equation y ax bx c that has slope 14 at x 1 slope 18 at x 1 and passes through the poi

Calculus
Differential equationsQuestion 13 Describe a function g x in terms of f x if the graph of g is obtained by reflecting the graph of f about the x axis and if it is horizontally stretched by a factor of 5 when compared to the graph of f g x Af Bx C where A B C
Calculus
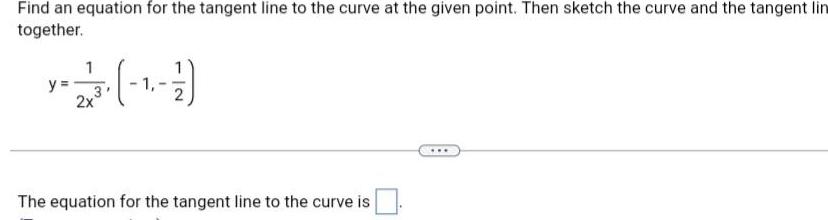
Differential equationsFind an equation for the tangent line to the curve at the given point Then sketch the curve and the tangent lin together y 223 1 1 2x The equation for the tangent line to the curve is

Calculus
Differential equations2 Calculate Brady s yards per attempt YPA YPA Total Passing Yards Total Passing Attempts YPA 79 204 10 598 YPA 7 47 3 Calculate Brady s touchdown percentage TD TD Total Touchdown Passes Total Passing Attempts 100 TD 581 10 598 100 TD 5 48 4 Calculate Brady s interception percentage INT INT Total Interceptions Total Passing Attempts 100 INT 191 10 598 100 INT 1 80 Now use these values to calculate Brady s passer rating using the NFL s formula Passer Rating CMP 30 20 YPA 3 4 TD 20 INT 25 Passer Rating 63 88 30 20 7 47 3 4 5 48 20 1 80 25 Passer Rating 33 88 20 4 47 4 109 6 45 Passer Rating 1 694 1 117 109 6 45 Passer Rating 112 411

Calculus
Differential equationsexampie Show that the points collinear Solution Direction ratios of line joining A and B are 1 2 2 3 3 4ie 1 5 7 1 It is clear that direction ratios of AB and BC are proportional hence AB is parallel to BC But point B is common to both AB and BC Therefore A B C are collinear points The direction ratios of line joining B and Care 3 1 8 2 11 3 ie 2 10 14 EXERCISE 11 1 1 If a line makes angles 90 135 45 with the x ya direction cosines 2 Find the direction cosines of a line which makes equal angles with the coordinate axes 3 If a line has the direction ratios 12 4 then what are its direction cosines 4 Show that the points 2 3 4 1 2 1 5 8 7 are collinear 5 Find the direction cosines of the sides of the triangle whose vertices are 3 5 4 1 1 2 and 5 5 2 11 3 Equation of a Line in Space We have studied equation of lines in two dimensions in Class XI we shall now study the vector and cartesian equations of a line in space A line is uniquely determined if 1 it passes through a given point and has given direction or n it passes through two given points 382 11 3 1 Equation of a line through a given point and parallel to a given vector b Let be the position vector of the given point A with respect to the origin O of the rectangular coordinate system Let be the line which passes through the point A and is parallel to a given vector b Let be the position vector of an arbitrary point P on the line Fig 11 3 wish But 1 0 MATHEMATICS Then AP is parallel to the vector b i e APA b where is some real number AP OP DA b 7 Conversely for each value of the parameter A this equation gives the position vector of a point P on the line Hence the vector equation of the line is given by X Rationalised 2023 24 s respectively find its and a 2 Fig 11 3 Y F a b Remark If hai b ck then a b c are direction ratios of the line and conversely if a b c are direction ratios of a line then b al by ck will be the parallel to the line Here b should not be confused with lb Derivation of cartesian form from vector form Let the coordinates of the given point A be x y z and the direction ratios of the line be a b c Consider the coordinates of any point P be x y z Then x t v t thit xitritzk b ai bj ck Substituting these values in 1 and equating the coefficients of i and k we get x x g v v b 2 2 kc 2

Calculus
Differential equations26 8 3 NT 0 C 4 B 8 A 2 A 6 C 0 C 4 A 1 2 8 8 B H 2 tan B C 2 sin 2A 31 D 35 C 39 B 43 D 47 C 51 B 55 B 59 D 63 C 27 m x 1 65 13 FI4 e TL 29 0 2nn 32 D 36 B 40 D 44 C 48 C 52 C 56 A DBD 60 1 4 12 14 3 a 1 2 a 4 66 3 3 8 True 69 False 70 False 2 False 73 True 74 True 6 a iv b i c ii d iii 5 bl 33 C 37 C 41 D 45 B 49 B 53 C 57 B 61 110 8 67 2 71 True 75 True

Calculus
Differential equations7 Information about a function f x is given in the table f 2 Decreasing 0 x 3 x 3 3 x 5 x 55 x Increasing 11 Increasing 5 a For which value s of e if any does f x have a relative local minimum b For which value s of x if any does f x have a relative local maximum

Calculus
Differential equations8 01 2 C 90 x C 10 2log x 1 C 12 14 17 1 Zet C 2e 20 log e C 29 x 4 x 8 C x 0 4 n c log x 1 m 22 tan 7 4x C 24 log 2sinx 3cos x C 26 2sin x C 32 37 C 15 1 3 39 B log sin x x 1 28 18 C 34 2v tanx C 35 cos tan x C I 13 18 2 3x log19 4x 1 C 16 C g cos x sin x C NCERT sin 4x 10 C 6 in 2x C 1 log x C Rationalised 2023 24 19 log e 1 C 30 log 1 cos x C 31 1 cos x otto e repurushed EXERCISE 7 3 sin 12x x sin 8x sin 4x C 8 4 cos 2x 1 cos 2x 1 C 25 tan 2x 3 x C sin x C 4 1 1 tan x 33 28 2 1 sin x C x 1 2 2 C 38 D 36 x log x C log cos x sin x C cos ANSWERS cos 7x cosx C 4 441
Calculus
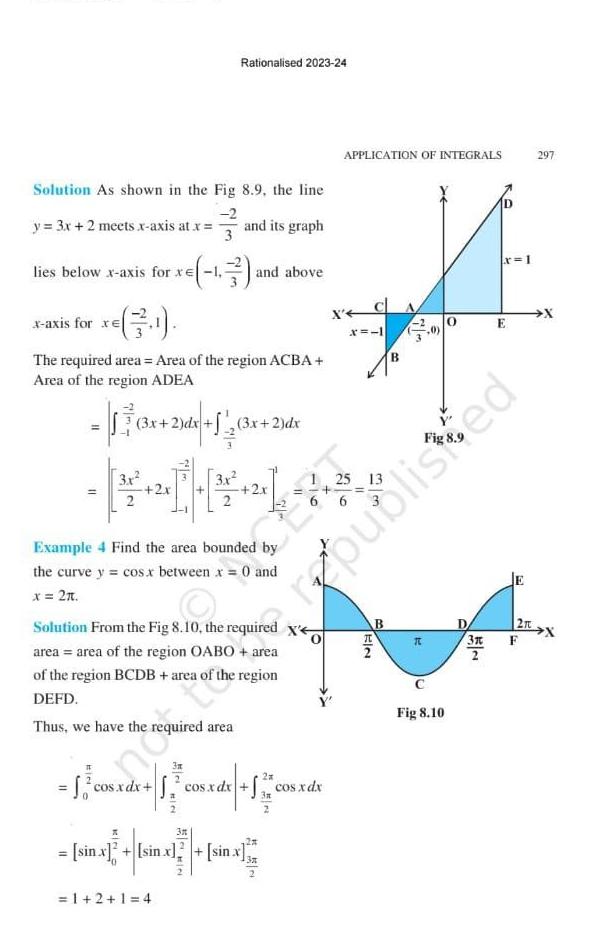
Differential equationsSolution As shown in the y 3x 2 meets x axis at x lies below x axis for xe x axis for xe 3 11 1 The required area Area of the region ACBA Area of the region ADEA 3x 2 dx 3 x Rationalised 2023 24 Fig 8 9 the line 2 and its graph 2 dx 3x 2 dx 1 2 1 4 and above Example 4 Find the area bounded by the curve y cos x between x 0 and x 2t 3n 0 Solution From the Fig 8 10 the required x area area of the region OABO area of the region BCDB area of region DEFD Thus we have the required area 2x cos xdx 1 cos x dx cos xdx cos xdx X sin x sin x sin x sin x APPLICATION OF INTEGRALS X CA 24 6 x 1 EIN B B 3 T 6 Fig 8 10 0 x 1 3x E republisted 1 2rt 297 F

Calculus
Differential equationslim Evaluate the Given limit 2x Answer 0 At x 2 the value of the given rational function takes the form 0 lim x 81 x 3 x 3 x 9 lim 2x 5x 3 al x 3 2x 1 x 3 x 9 Question 9 Answer Question 10 lim lim Evaluate the Given limit cx 1 lim 1 2x 1 Answer 3 3 3 9 2 3 1 ax b a 0 b lim cx 1 c 0 1 6x18 7 108 7 Evaluate the Given limit lim Accordingly lim 1 lim 2441 H ax b lim 2 4 At z 1 the value of the given function takes the form 0 Put x so that z 1 as x 1 lim 44 21h lim 13 0
Calculus
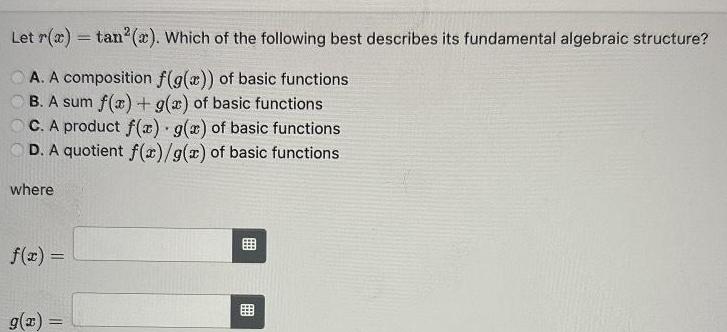
Differential equationsLet r x tan x Which of the following best describes its fundamental algebraic structure A A composition f g x of basic functions B A sum f x g x of basic functions C A product f x g x of basic functions D A quotient f x g x of basic functions where f x g x B
Calculus
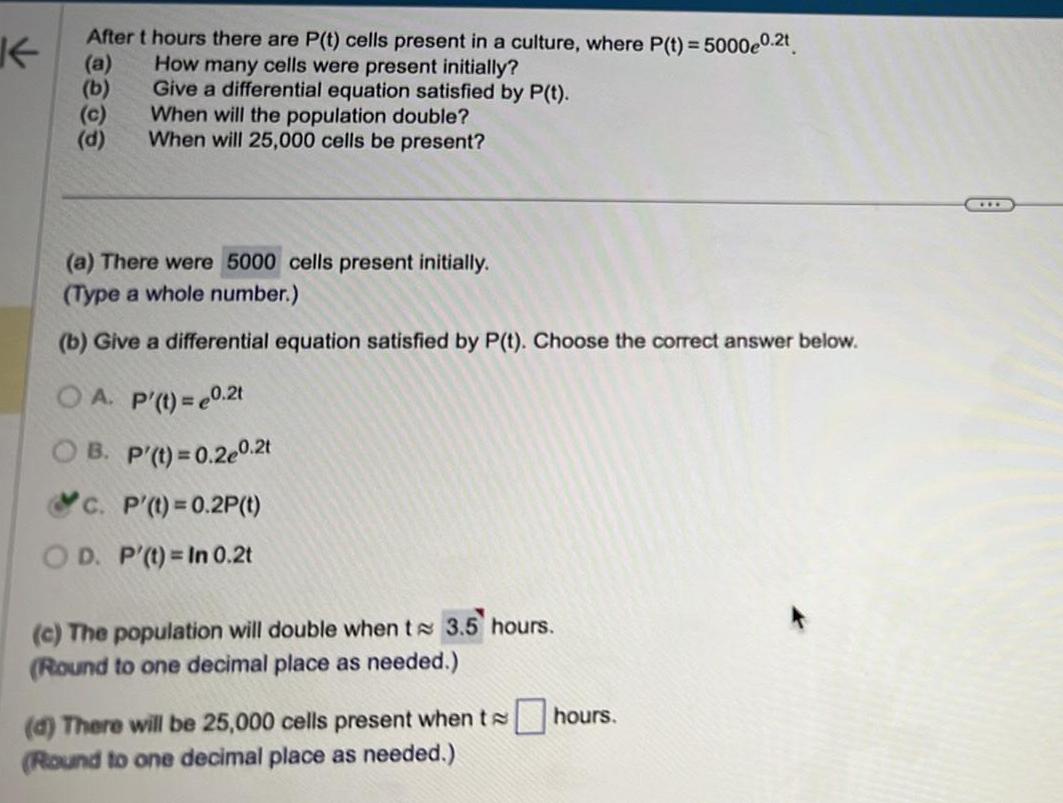
Differential equationsK After t hours there are P t cells present in a culture where P t 5000e0 2t a How many cells were present initially Give a differential equation satisfied by P t When will the population double When will 25 000 cells be present c d a There were 5000 cells present initially Type a whole number b Give a differential equation satisfied by P t Choose the correct answer below OA P t 0 2t B P t 0 2e0 2t c P t 0 2P t OD P t In 0 2t c The population will double when te 3 5 hours Round to one decimal place as needed d There will be 25 000 cells present when thours Round to one decimal place as needed
Calculus
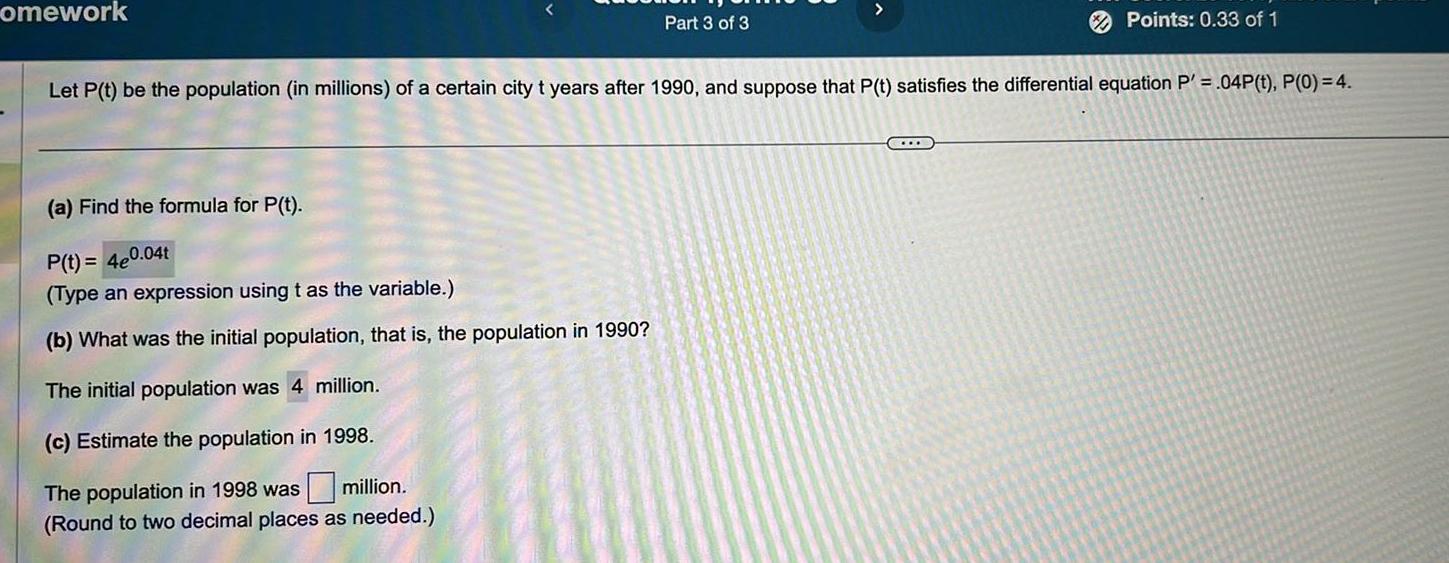
Differential equationsomework Part 3 of 3 a Find the formula for P t P t 4e0 04t Type an expression using t as the variable b What was the initial population that is the population in 1990 The initial population was 4 million c Estimate the population in 1998 The population in 1998 was million Round to two decimal places as needed Points 0 33 of 1 Let P t be the population in millions of a certain city t years after 1990 and suppose that P t satisfies the differential equation P 04P t P 0 4
Calculus
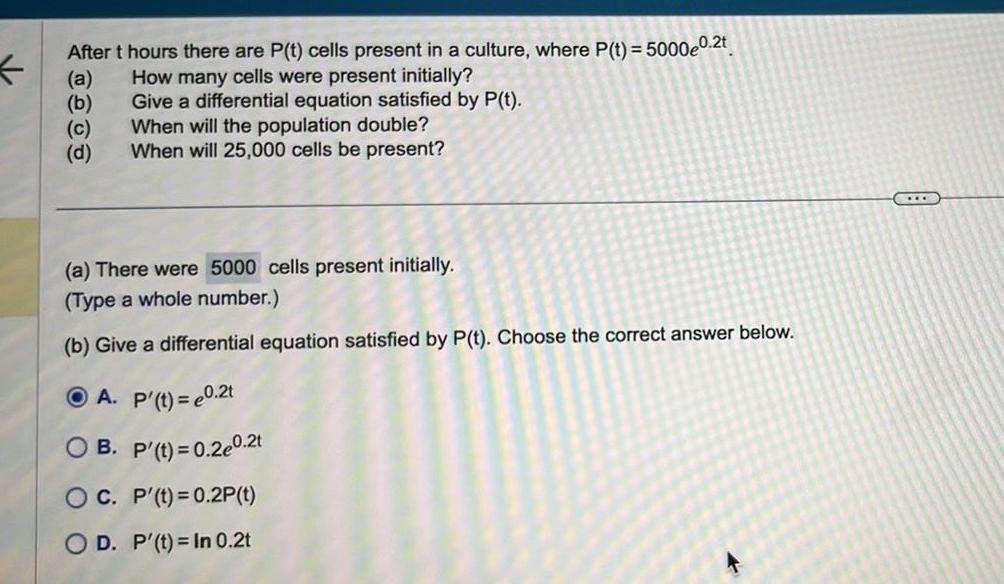
Differential equationsAfter t hours there are P t cells present in a culture where P t 5000e0 2t How many cells were present initially Give a differential equation satisfied by P t When will the population double When will 25 000 cells be present a b c d a There were 5000 cells present initially Type a whole number b Give a differential equation satisfied by P t Choose the correct answer below A P t 0 2t OB P t 0 2e0 2t OC P t 0 2P t OD P t In 0 2t
Calculus
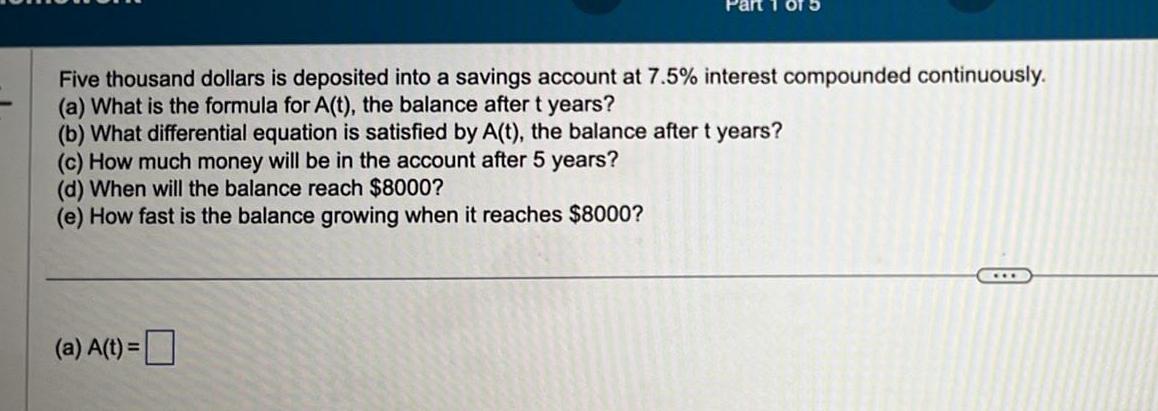
Differential equationsFive thousand dollars is deposited into a savings account at 7 5 interest compounded continuously a What is the formula for A t the balance after t years b What differential equation is satisfied by A t the balance after t years c How much money will be in the account after 5 years d When will the balance reach 8000 e How fast is the balance growing when it reaches 8000 a A t

Calculus
Differential equationsdL The intensity L x of light x feet beneath the surface of the ocean satisfies the differential equation dx From experience a diver knows that diving to 19 ft in a sea cuts the intensity in half He cannot work without artificial light when the intensity falls below one tenth of the surface value About how deep can he expect to work without artificial light He can work approximately ft deep without artificial light Simplify your answer Round to the nearest tenth as needed KL
Calculus
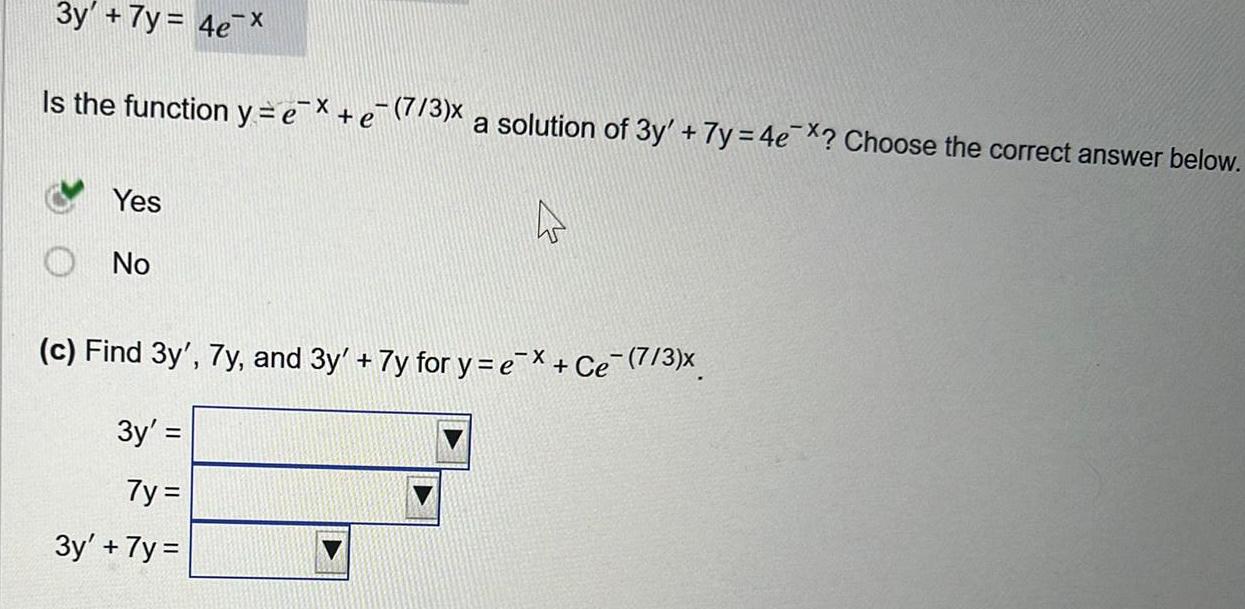
Differential equations3y 7y 4e X Is the function y e Yes No 7 3 x a solution of 3y 7y 4e Choose the correct answer below 4 c Find 3y 7y and 3y 7y for y e e 7 3 3y 7y 3y 7y
Calculus
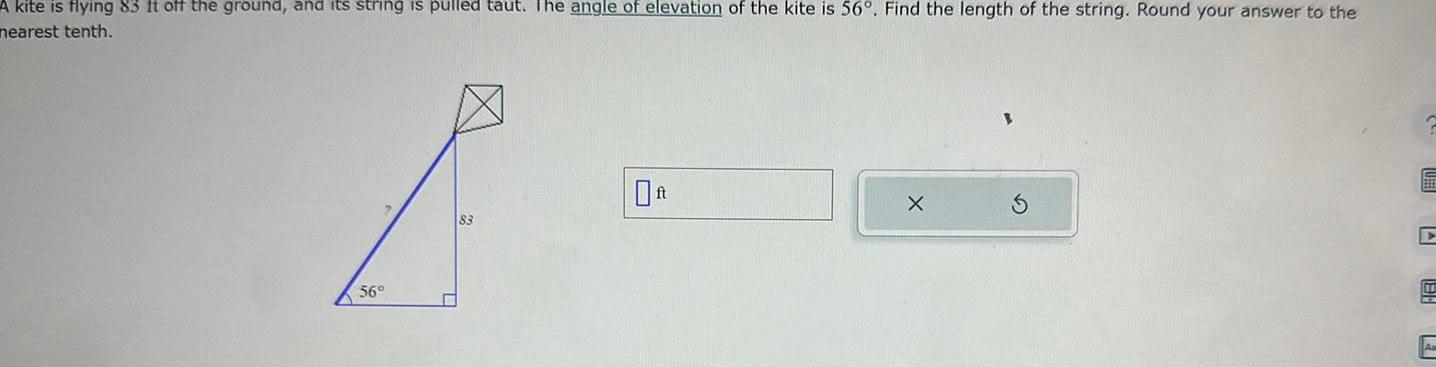
Differential equationsA kite is flying 83 ft off the ground and its string is pulled taut The angle of elevation of the kite is 56 Find the length of the string Round your answer to the nearest tenth 56 83 X S HB P

Calculus
Differential equationsSolve the differential equation dy dx 11 1 2 y cos y COS The solution is
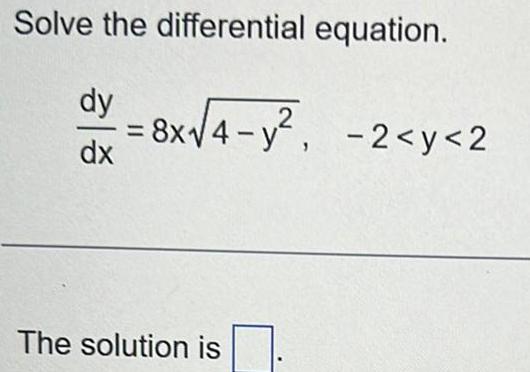

Calculus
Differential equationsCheck whether each of the following functions is a solution of the differential equation 3y 7y 4e x X b y e e 7 3 x a y ex c y ex Ce 7 3 x a Find 3y 7y and 3y 7y for y ex 3y 7y 3y 7y

Calculus
Differential equations63 78 Find the derivative of the function Simplify where possible 63 f x sin 5x 65 y tan x 1 64 g x sec e 66 y tan x

Calculus
Differential equations1 log 1 x C 4 cos cos x C 440 8 12 11 x 4 x 8 C 3 14 17 2 6 ax b C 7 x 2 x 2 C 3a 20 22 MATHEMATICS 32 log x l m 1 m 37 1 2e 1 2x C 9 x x 1 C 9 C 26 2sin x C C log e x e x C 1 29 log sin x C x 2 x 14 x 1 C tan 7 4x C 4 39 B 2 5 1 2 24 log 2 sin x 3 cos x C 15 4 3 logl x C cos tan x C 4 4a cos 2 ax b C Rationalised 2023 24 18 etan x C 8 3 34 2 tan x C 35 1 log x C 3 log 1 log x C 10 2log x 1 C e2x 3 log19 4x 1 C 16 3 C NCERT 13 Rationalised 2023 24 19 log e log 1 cos x C 31 25 1 18 2 3x 33 1 1 tan x 28 2 1 sinx C X tan 2x 3 x C 1 sin x C 1 1 cos x 38 D 1 C 22 C C otto e republished log cos x sinx C 36 x log x C 3

Calculus
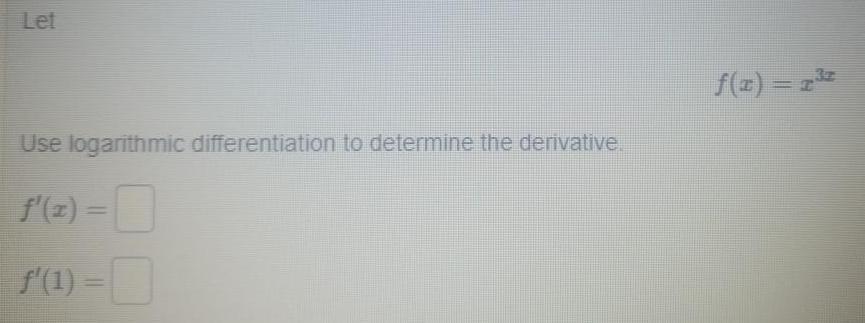
Differential equationsLet Use logarithmic differentiation to determine the derivative f x 1 f x 2
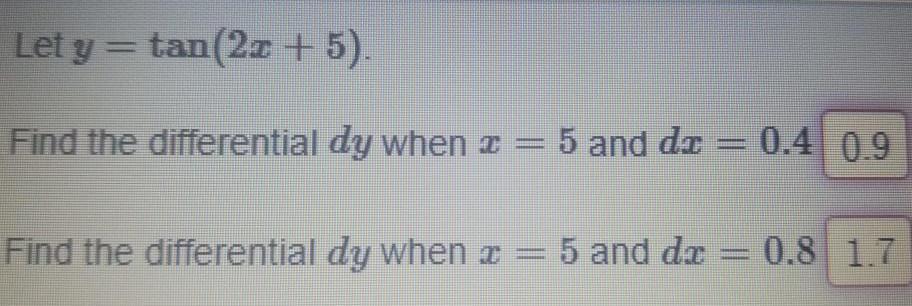
Calculus
Differential equationsLet y tan 2x 5 Find the differential dy when z 5 and di Find the differential dy when 5 and dr 0 4 0 9 0 8 1 7

Calculus
Differential equationsLet f and g be inverse functions The following table lists a few values of f g and f 30 2 f x g x f x 19 9 2 10 g 2 13 12 12

Calculus
Differential equations4 5 6 7 3 Transter Certificate T C Character Certificate C C Migration Certificate Bonafied Certificate Caste Certificate Aadhar Card Photo Copy
Calculus
Differential equationsHello there we sincerely apologize for any inconvenience caused by the delay in processing your payment We have already processed payments up to the 23rd of August We understand that you may have been eagerly awaiting the remaining payments and we want to assure you that they will be processed very soon We appreciate your patience and support as we work to resolve this matter Thank you for your understanding and please do not hesitate to reach out to us if you have any further concerns or questions
Calculus
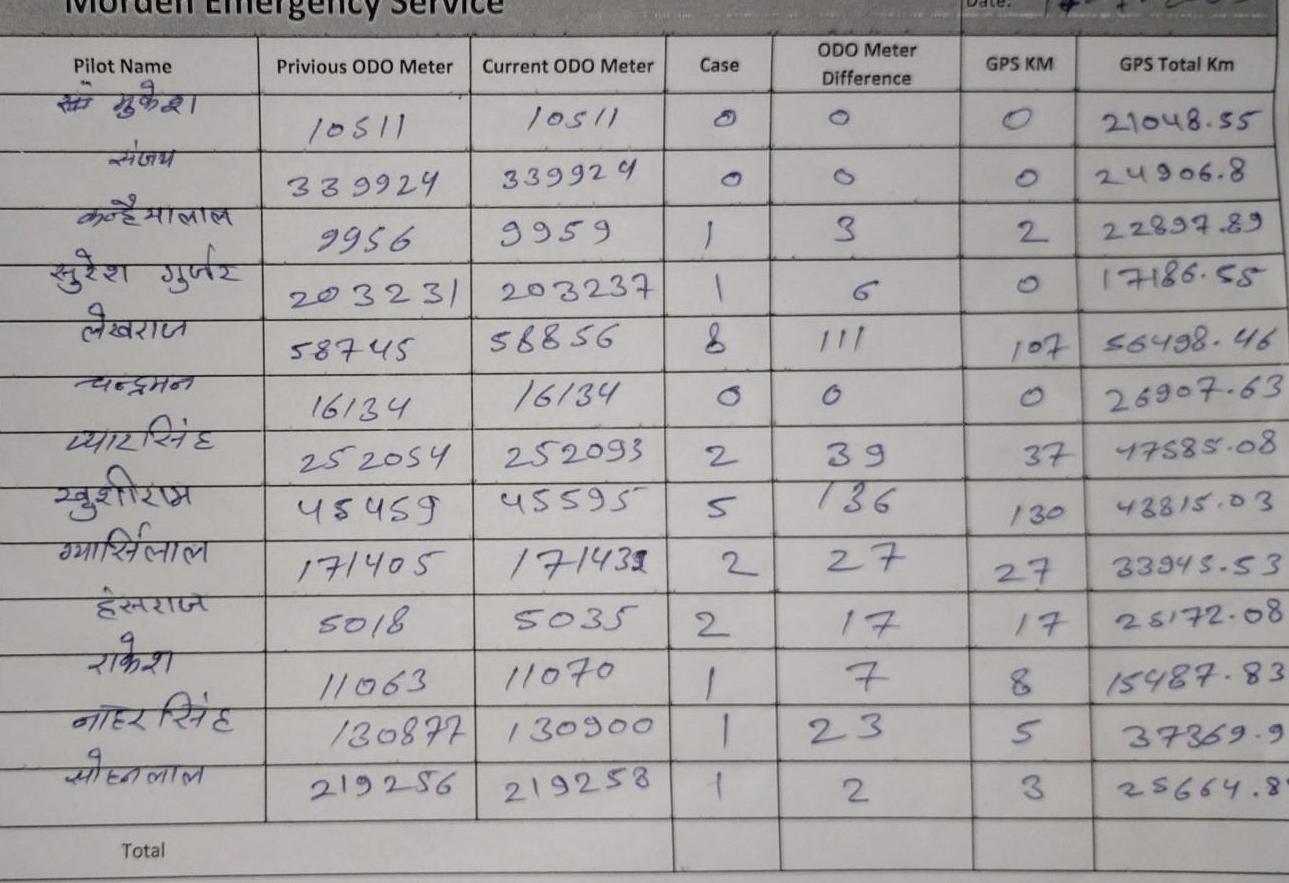
Differential equationsPilot Name 3 nhal LIGH gear shofe RIC 46GH THIRRJE zgertzen SZIG 2127 GITEZ PE Total Privious ODO Meter Current ODO Meter 10511 339929 9956 203231 58745 16134 252054 45459 171405 5018 los 1 339924 9959 203237 58856 16 34 252093 45595 171439 5035 11063 11070 130877 130900 219256 219258 Case J 1 O 2 5 2 2 1 1 1 ODO Meter Difference 0 3 6 39 736 27 17 73 7 23 2 GPS KM 2 37 107 56498 46 26907 63 47585 08 43815 03 130 27 17 8 5 GPS Total Km 3 21048 55 24906 8 22897 89 17186 55 33945 53 28172 08 15487 83 37369 9 25664 8
Calculus
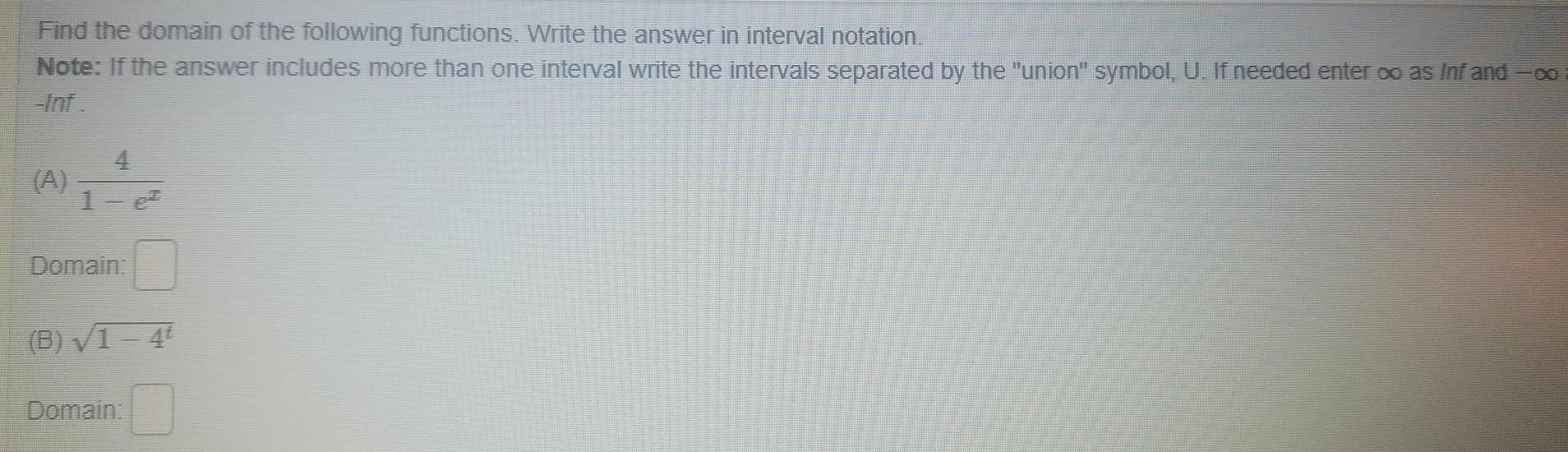
Differential equationsFind the domain of the following functions Write the answer in interval notation Note If the answer includes more than one interval write the intervals separated by the union symbol U If needed enter o as Infand co Inf A 4 1 e Domain B 1 4t Domain

Calculus
Differential equationsII I Discontinuity of the First Kind from the Left at x The function f X R is said to have a discontinuity of first kind from the left at x if the left hand limit exist at x but not equal to the value of the function at x i e lim f x f x II II Discontinuity of the First Kind from the Right at The function f X R is said to have a discontinuity of first kind from the right atx if the right hand limit exist at x but not equal to the value of the function atx i e lim f x f x X III Discontinuity of the Second Kind at x The function f X R is said to have a discontinuity of second kind at if both the left hand limit and right hand limit do not exist at x i e lim f x and lim f x do not exist III I Discontinuity of the Second Kind from the Left at x The function f X R is said to have a discontinuity of second kind from the left at x if the left hand limit does not exist at x i e lim f x does not exist X x III II Discontinuity of the First Kind from the Right at x The function f X R is said to have a discontinuity of second kind from the right at x if the right hand limit does not exist at i e lim f x does not exist x Value Addition Jump of a Function at x If a function f X R has a discontinuity of first kind at x then the function f is said to have a jump at x and the value of the jump is equal to the difference of both the limits at x i e Institute of Lifelong Learning University of Delhi Value of the jump at x lim f x lim f x 1 94 1 g Example 5 Show that the function f defined by sin x Continuity of Functions f x x DEL x 0 x 0 dementimuit pg 10 10

Calculus
Differential equationsPart 1 The Partial Fraction Setup 4x 3 and find the values of the 3x 5 x 3 Perform the partial fraction decomposition of coefficients Give the coefficients as exact integers or fractions If you use a decimal number all answers will be marked as incorrect 4z 3 3x 5 2 3
Calculus
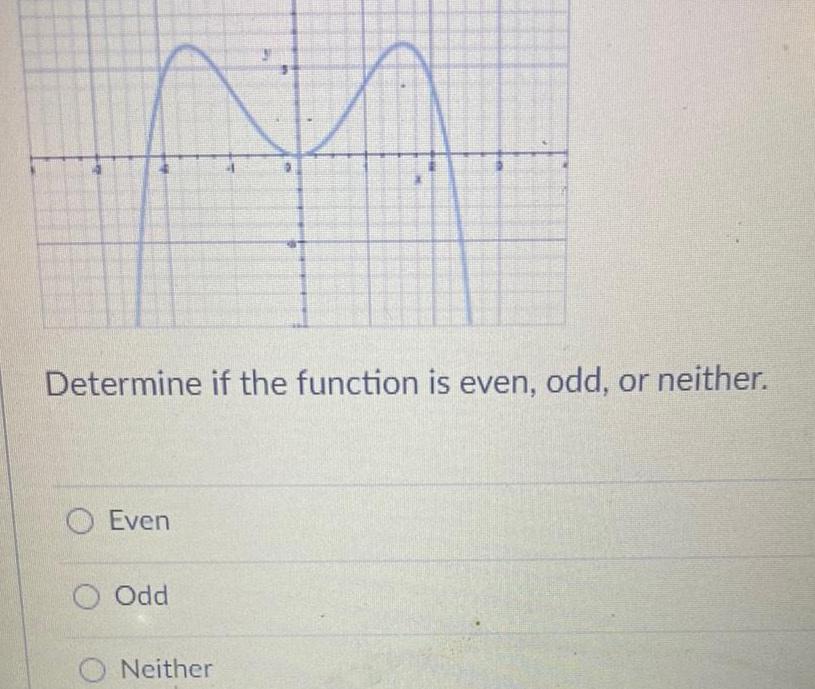
Differential equationsNA Determine if the function is even odd or neither Even O Odd ONeither

Calculus
Differential equations5 1 Types of Discontinuity Let f be a function defined as f X R and let xeX and let left hand limit right hand limit limit of the function and the value of the function at xoare denoted by lim f x lim f x lim f x and f x respectively Then I Removable Discontinuity at x at have th The function f X R is said to have the removable discontinuity at x EX if the limit of the function exist at x but not equal to the value of the function at x i e lim f x f x X 40 ata II Discontinuity of the First Kind at x The function f X R is said to have a discontinuity of first kind at x if both the left hand limit and right hand limit exist at x but are not equal to each other i e 799 lim f x lim f x DL

Calculus
Differential equationsThe graph of fis given State the numbers at which is not differentiable Enter your answers as a comma separated li than 0 2 4 e
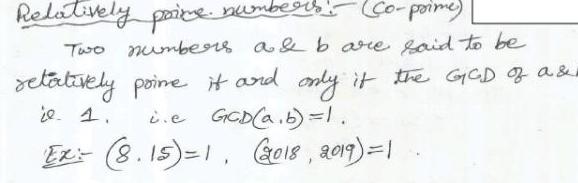
Calculus
Differential equationsRelatively paine numbers Co poime Two numbers a b are said to be retatively poine it and only if the GGD of a ie 1 ie GCD a b 1 2018 2019 1 Ex 8 15 1

Calculus
Differential equationsmust be used to obtain the particular solution desired here Since tan 10 0 and tan 1 c 0 7 Thus the solution of the initial value problem is 77 tan x tan y Let us look at another example Example 3 Solved Solution Let us write the given equation as 1 ky my2 dx dy 1 Let Now we will try to decompose the coefficient of dy into partial fractions 1 B y k my A yk my where A and B are constants to be determined From 6 we get 1 A k my By or 4 which gives 1 Ak and 1 M 1 ky my2 where k 0 and m 0 are real constants and R E Bk m 6

Calculus
Differential equationsFor the first order system above let u t 0 t0 0 and x 0 5 Use Simulink to solve the resulting system using an integrator block and rewriting the equation as dx t dt 1 2 1 cos t x t Compare your Simulink result to the closed form solution
Calculus
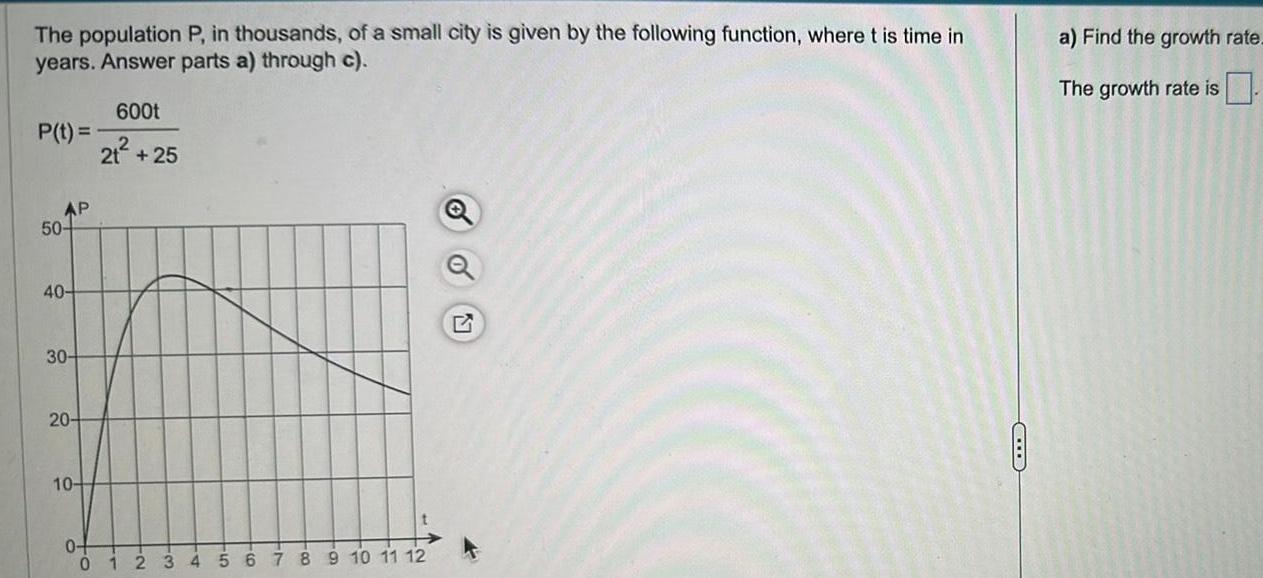
Differential equationsThe population P in thousands of a small city is given by the following function where t is time in years Answer parts a through c P t AP 50 40 30 20 10 0 0 600t 21 25 1 2 32 ti 56 78 9 10 11 12 a Find the growth rate The growth rate is

Calculus
Differential equationsIs the function g x continuous at x 9 G x 81 No O Yes x 9 19 for x 9 for x 9 Choose the correct answer below
Calculus
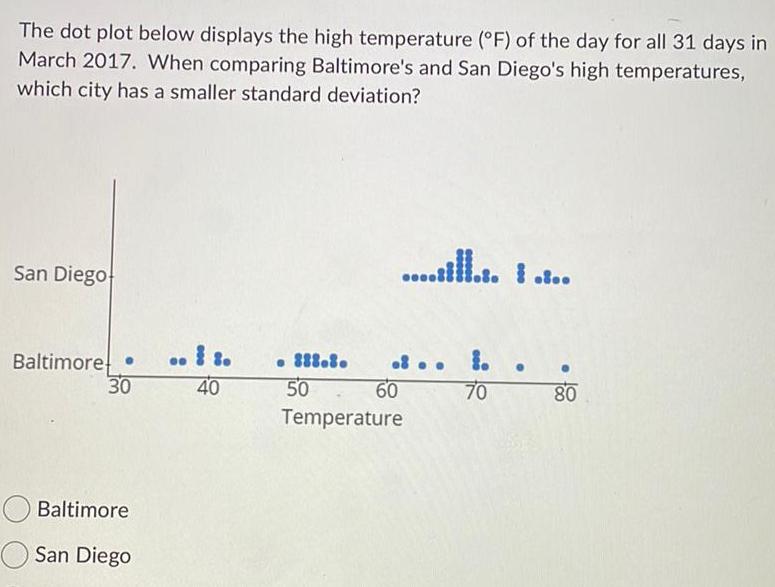
Differential equationsThe dot plot below displays the high temperature F of the day for all 31 days in March 2017 When comparing Baltimore s and San Diego s high temperatures which city has a smaller standard deviation San Diego Baltimore 30 Baltimore San Diego 40 888 8 50 Temperature 60 70 80

Calculus
Differential equations7 Let f x a Calculate f x for each value of x in the following table x 4 X b Make a conjecture about the value of lim X 11 2 4 X 2 1 9 12x 2 1 99 1 999 1 9999 2 1 2 01 2 001 2 0001
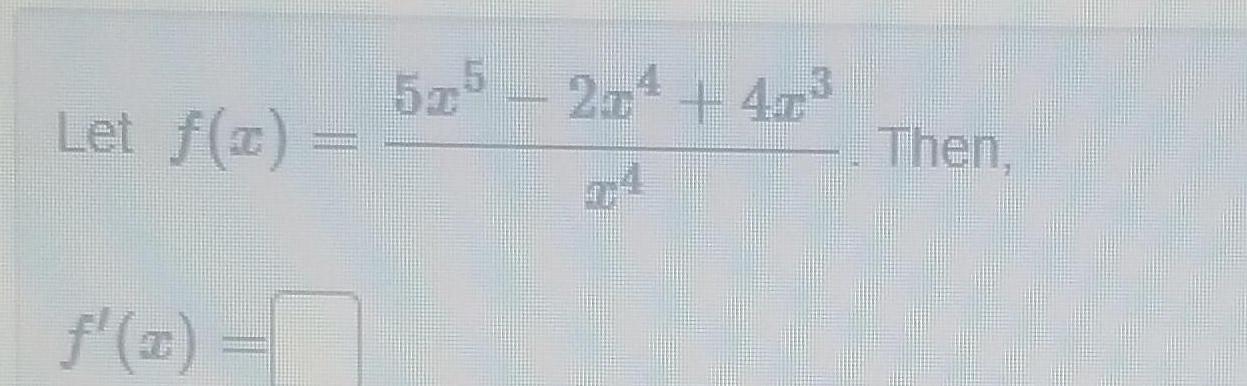
Calculus
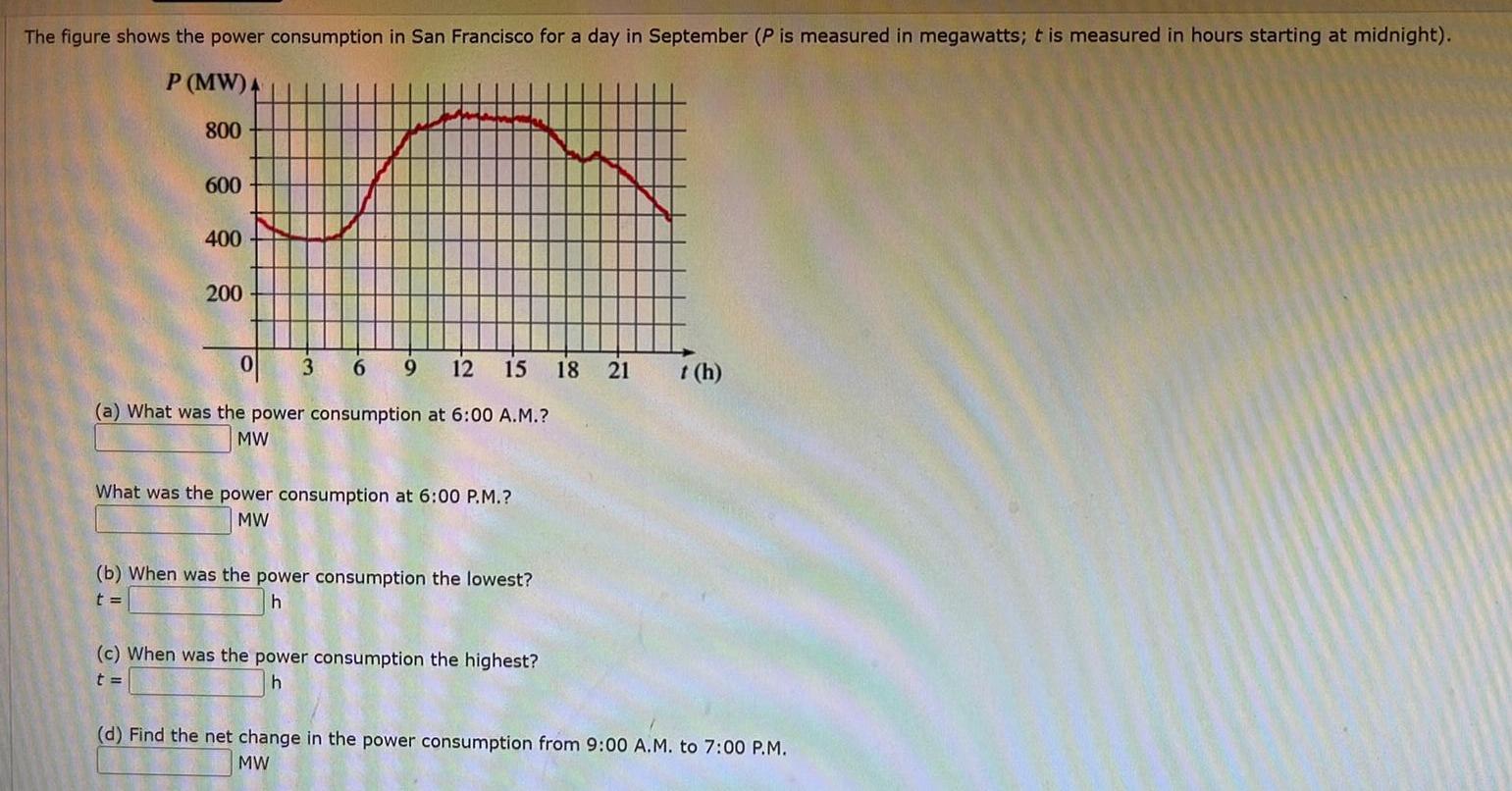
Differential equationsThe figure shows the power consumption in San Francisco for a day in September P is measured in megawatts t is measured in hours starting at midnight P MW 4 800 600 400 200 0 3 6 9 12 15 18 21 a What was the power consumption at 6 00 A M MW What was the power consumption at 6 00 P M MW b When was the power consumption the lowest t h c When was the power consumption the highest t h t h d Find the net change in the power consumption from 9 00 A M to 7 00 P M MW
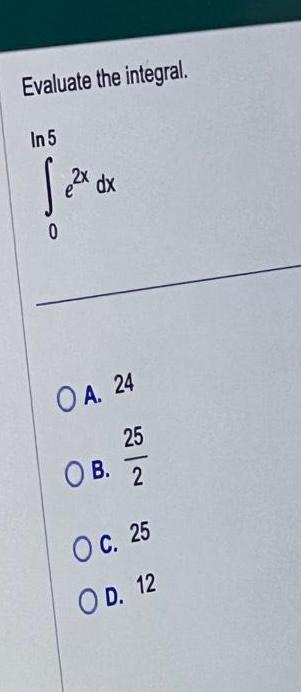

Calculus
Differential equationsEvaluate the integral fe cot e 6 dt O A e In sin t 6 C OB Incos e 6 C OC In sin 6 C OD In sin t 6 C

Calculus
Differential equationsIf construction costs are 144 000 per kilometer find the cost of building the new road in the figure shown to the right The cost of building the new road is s Round to the nearest dollar as needed new road 24 000 m 10 000 m

Calculus
Differential equationsDetermine whether the given function is a solution to the given differential equation d 0 de dt 8 4t 5t 0 40 12e5t dt