Differentiation Questions and Answers
Calculus
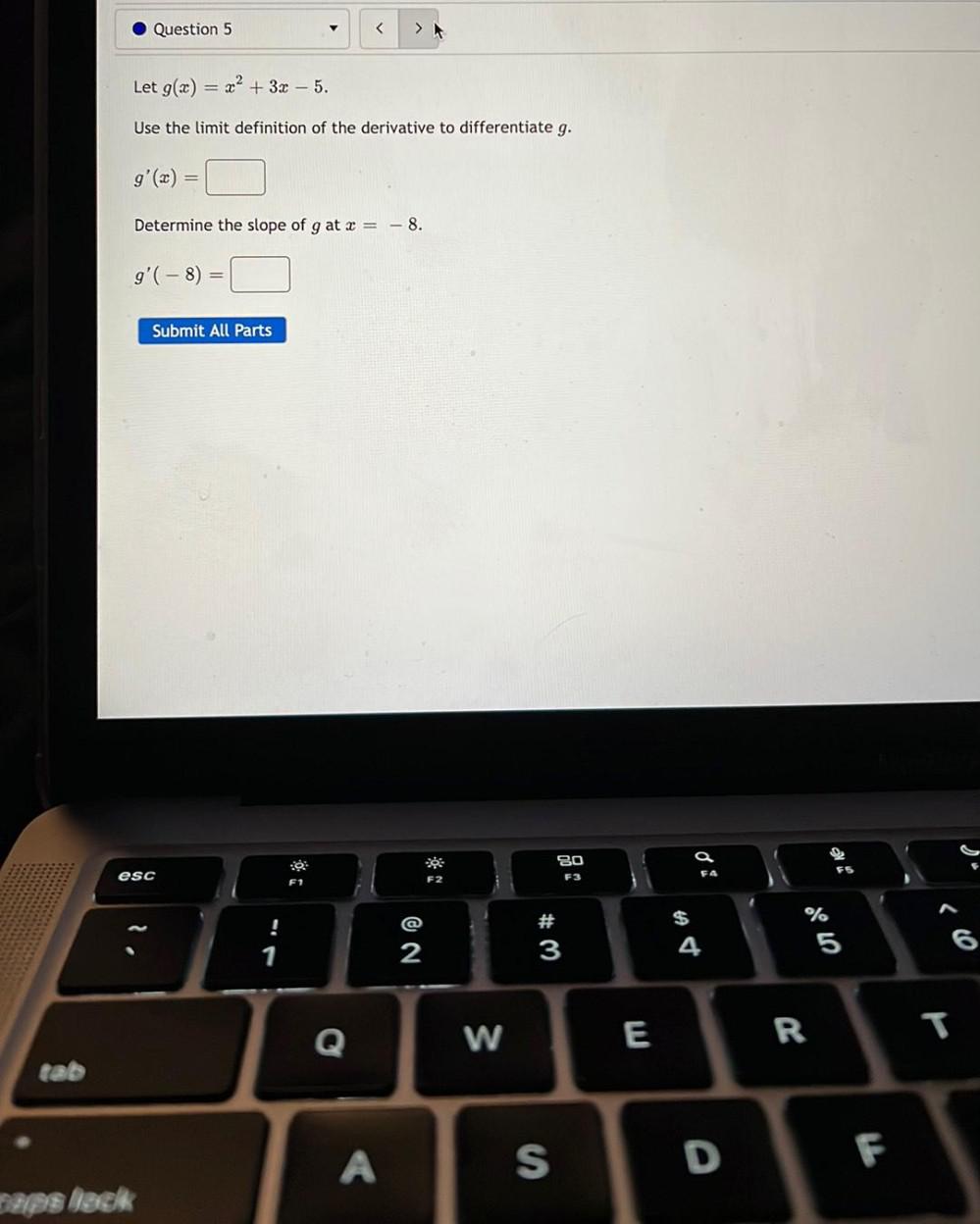
DifferentiationLet g(x) = x² + 3x - 5.
Use the limit definition of the derivative to differentiate g.
g'(x) =_______
Determine the slope of g at x = - 8.
g'(- 8) =_______
Submit All Parts
Calculus
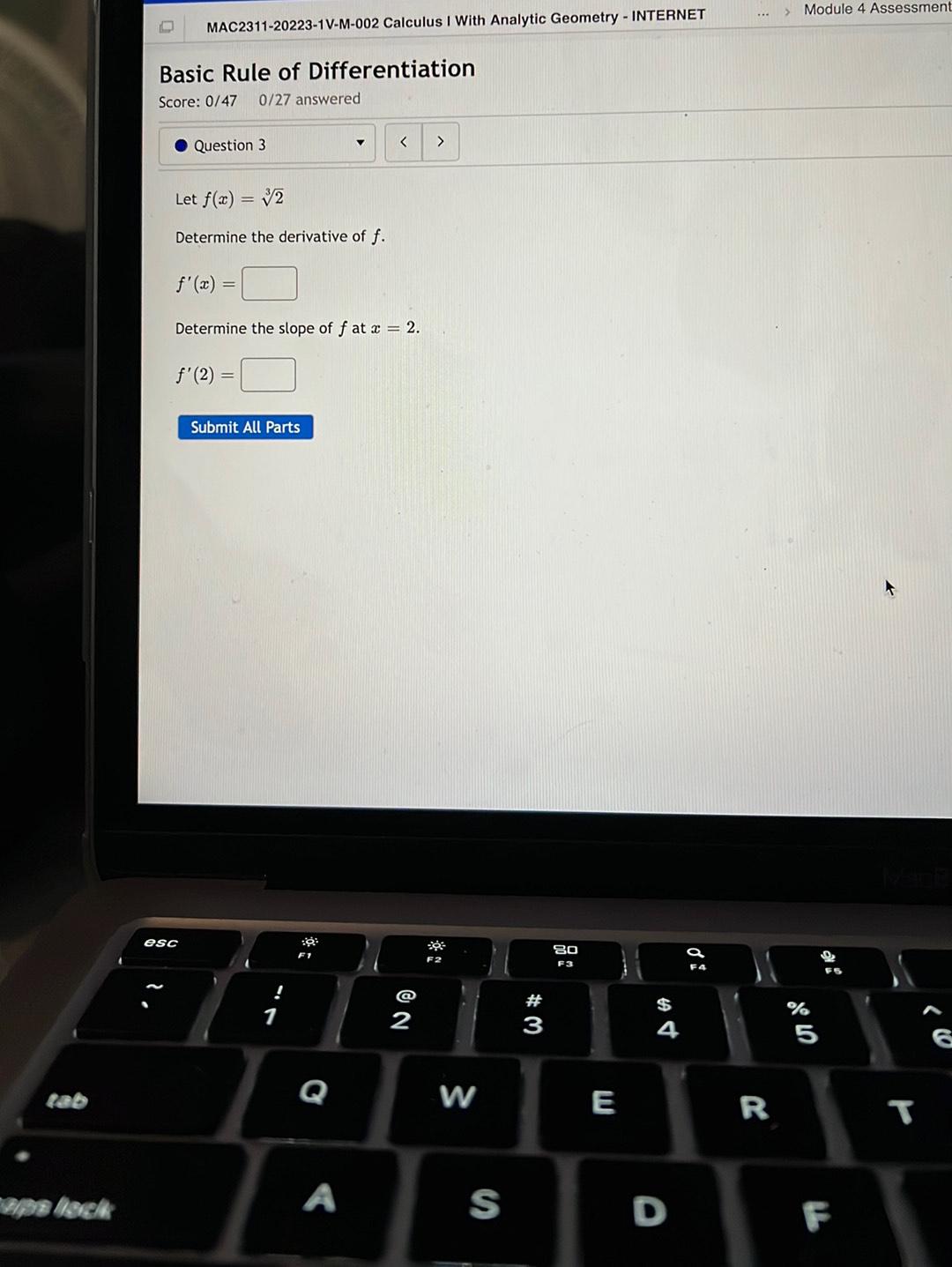
DifferentiationLet f(x) = ∛2
Determine the derivative of f.
f'(x) = ______
Determine the slope of f at x = 2.
f'(2) = _______
Calculus
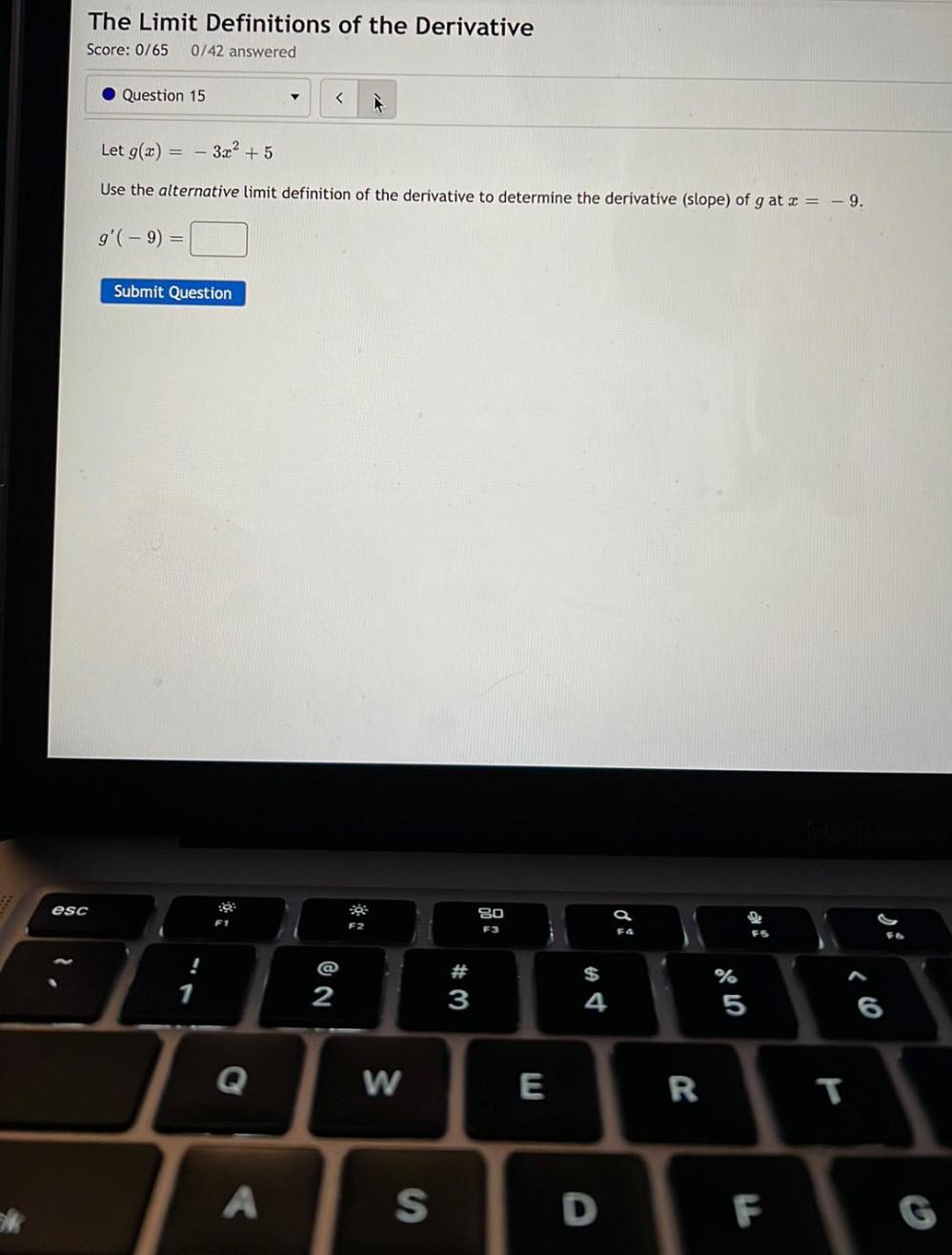
DifferentiationLet g(x)= -3x² + 5
Use the alternative limit definition of the derivative to determine the derivative (slope) of g at x = -9.
g'(- 9) =_______

Calculus
DifferentiationConsider the graph of f given below.
Evaluate the following limit.
lim △x->0 f(1+ △x) - f(1)/△x = ________
Calculus
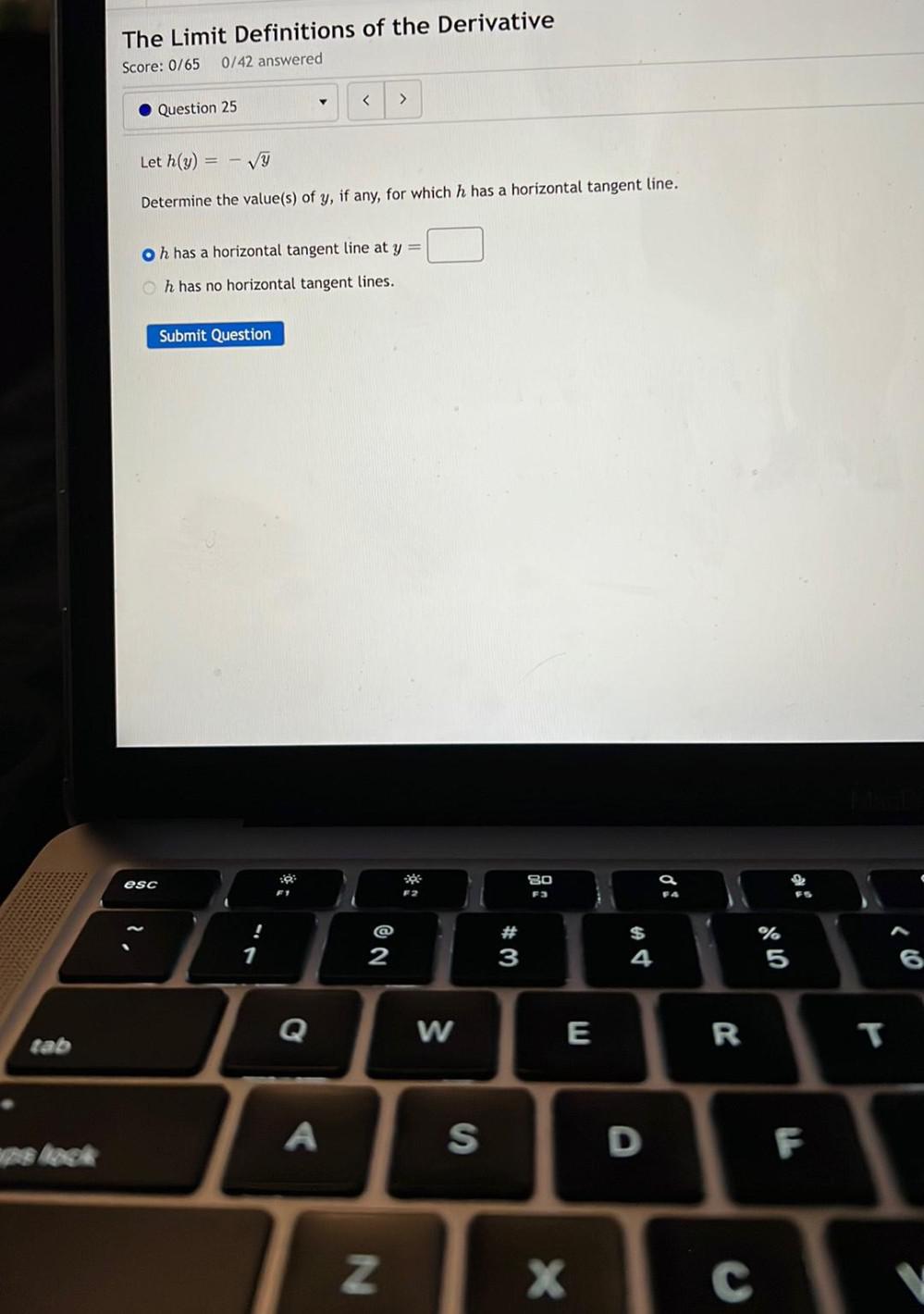
DifferentiationLet h(y) =- √Y
Determine the value(s) of y, if any, for which h has a horizontal tangent line.
○ h has a horizontal tangent line at y = □
○ h has no horizontal tangent lines.
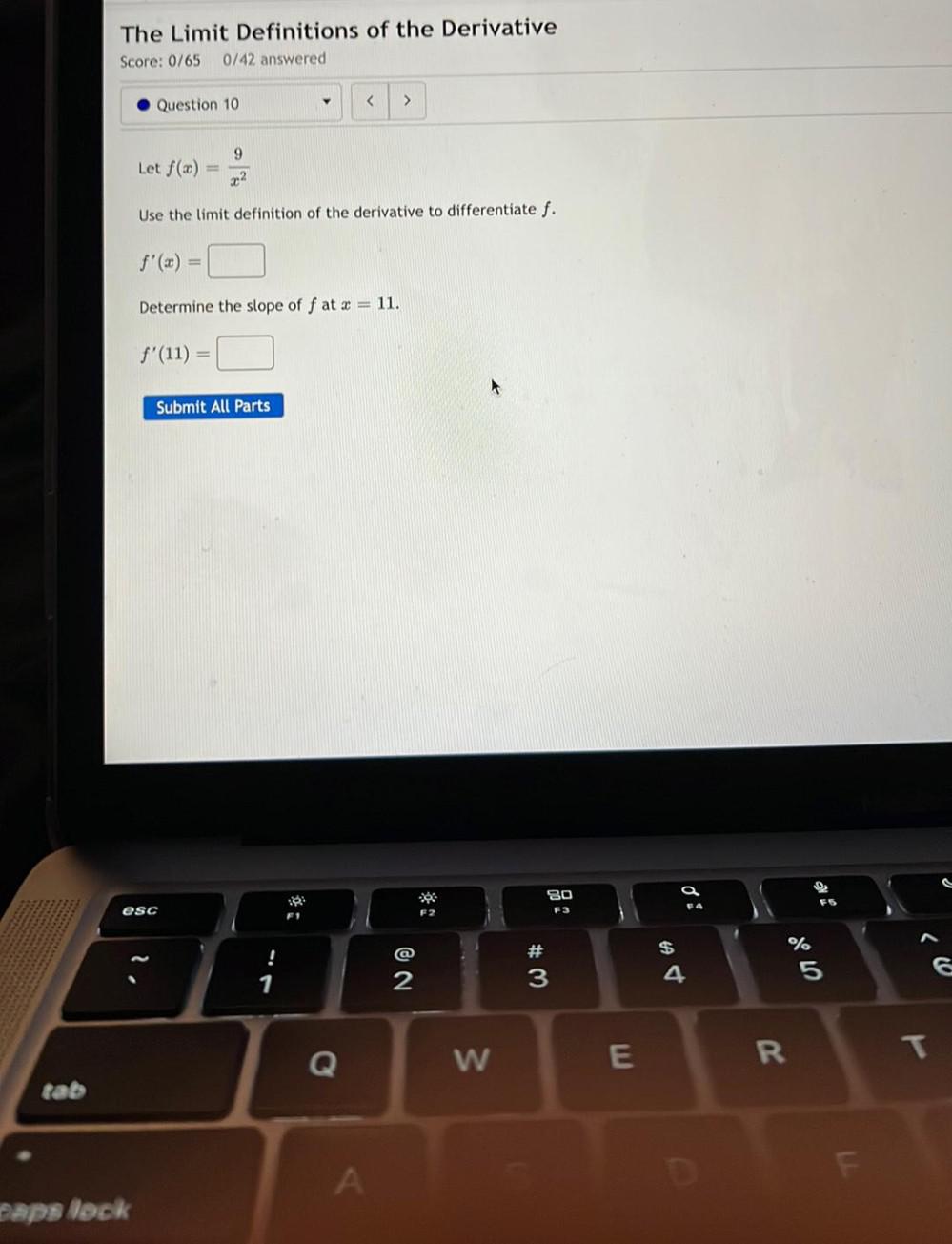
Calculus
DifferentiationLet f(x)=9/x²
Use the limit definition of the derivative to differentiate f.
f'(x)= □
Determine the slope of f at x = 11.
f'(11)= □
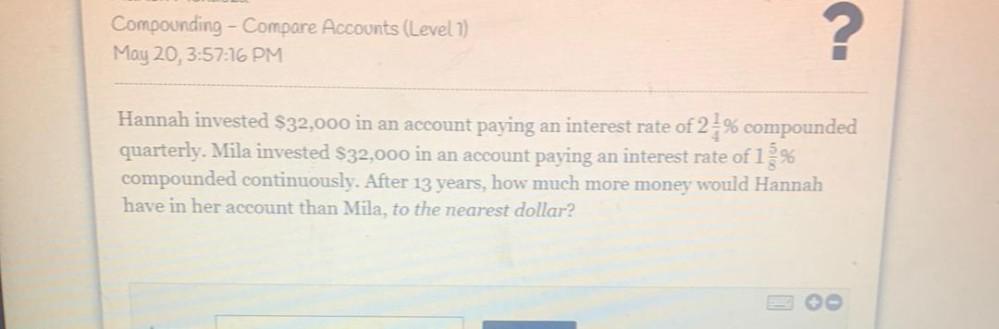
Calculus
DifferentiationHannah invested $32,000 in an account paying an interest rate of 2 ¼ % compounded quarterly. Mila invested $32,000 in an account paying an interest rate of 1⅝% compounded continuously. After 13 years, how much more money would Hannah have in her account than Mila, to the nearest dollar?
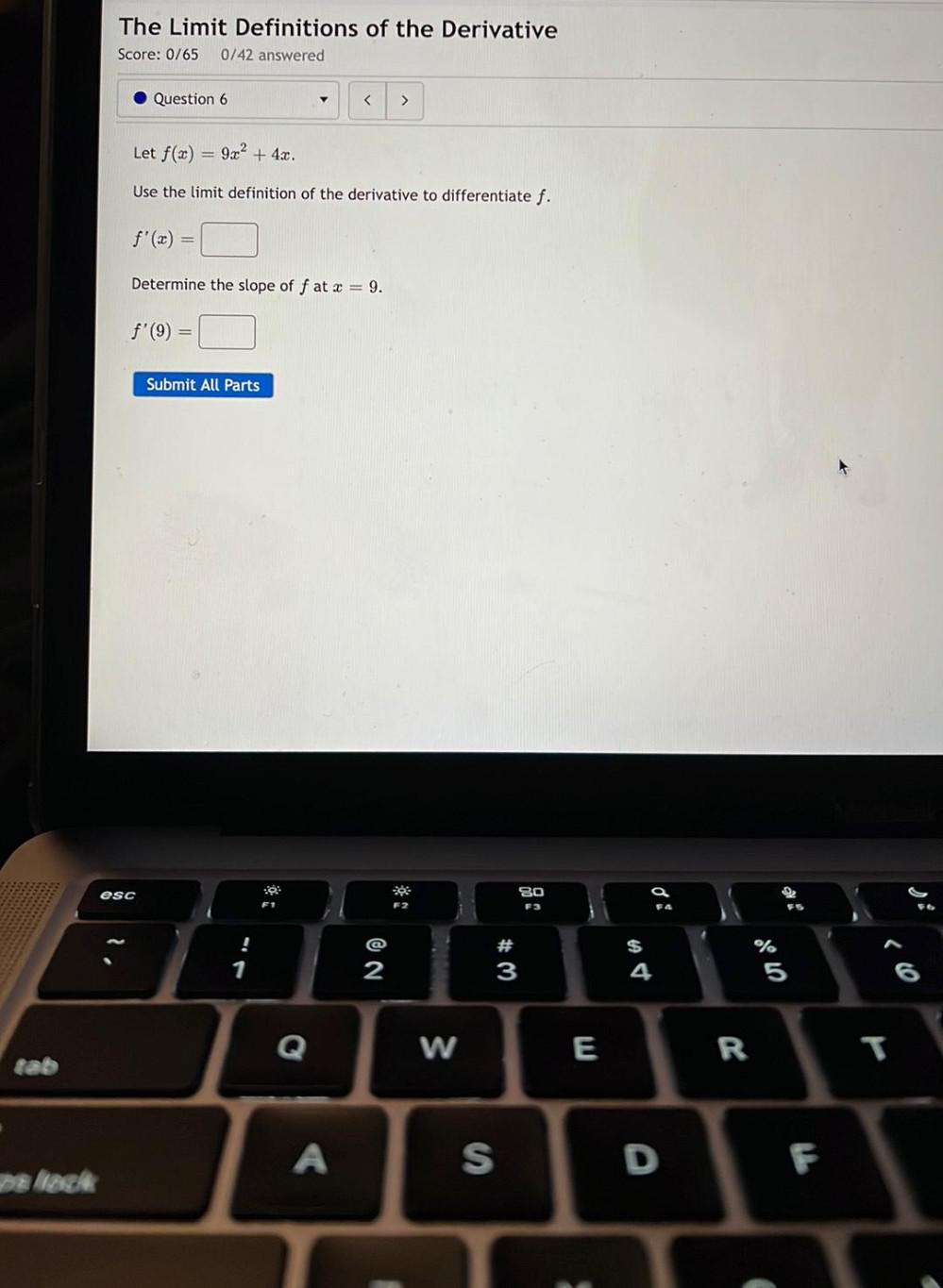
Calculus
DifferentiationLet f(x)=9x² + 4x.
Use the limit definition of the derivative to differentiate f.
f'(x) = □
Determine the slope of f at x = 9.
f'(9) = □
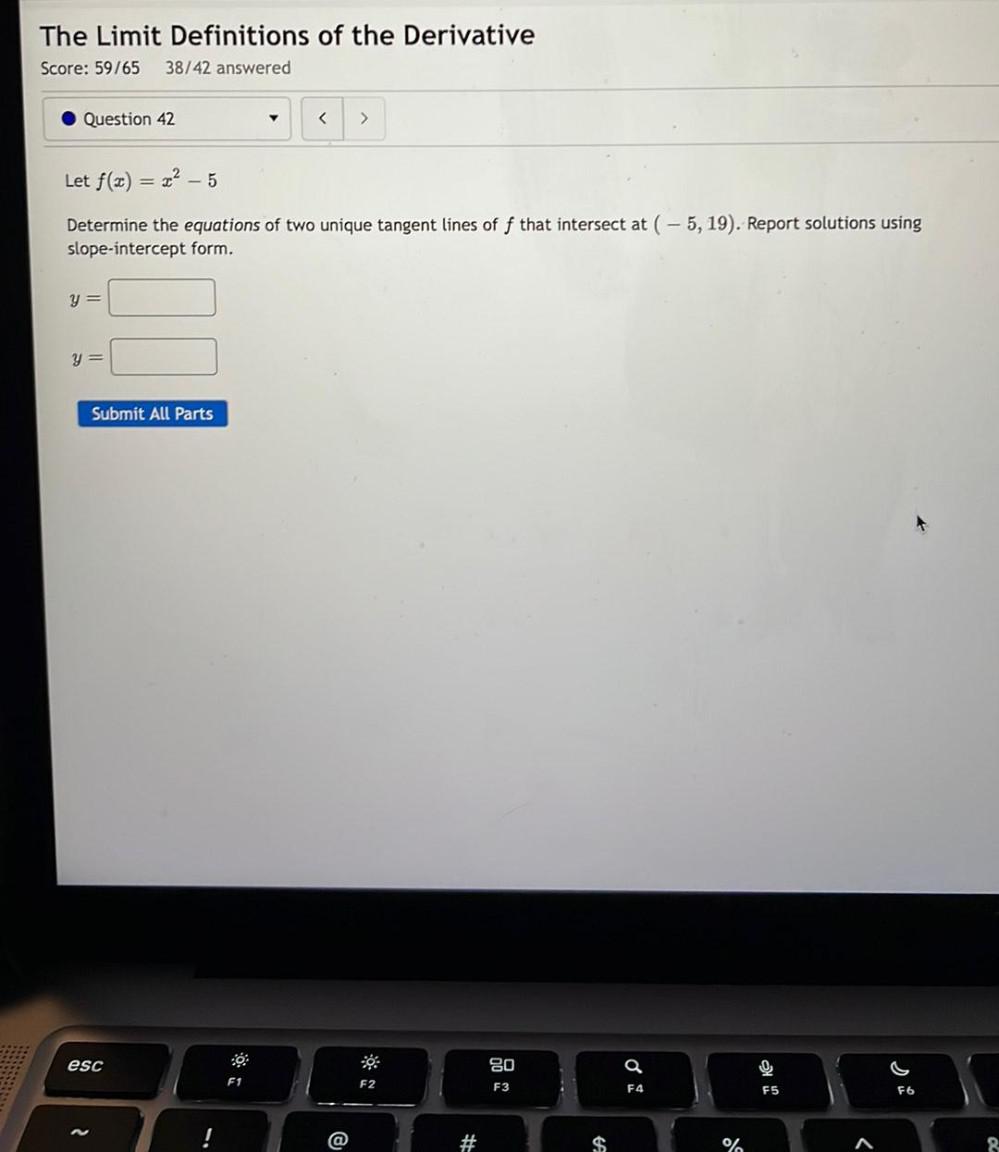
Calculus
DifferentiationLet f(x) = x² - 5
Determine the equations of two unique tangent lines of f that intersect at (-5, 19). Report solutions using slope-intercept form.
y =___
y =___
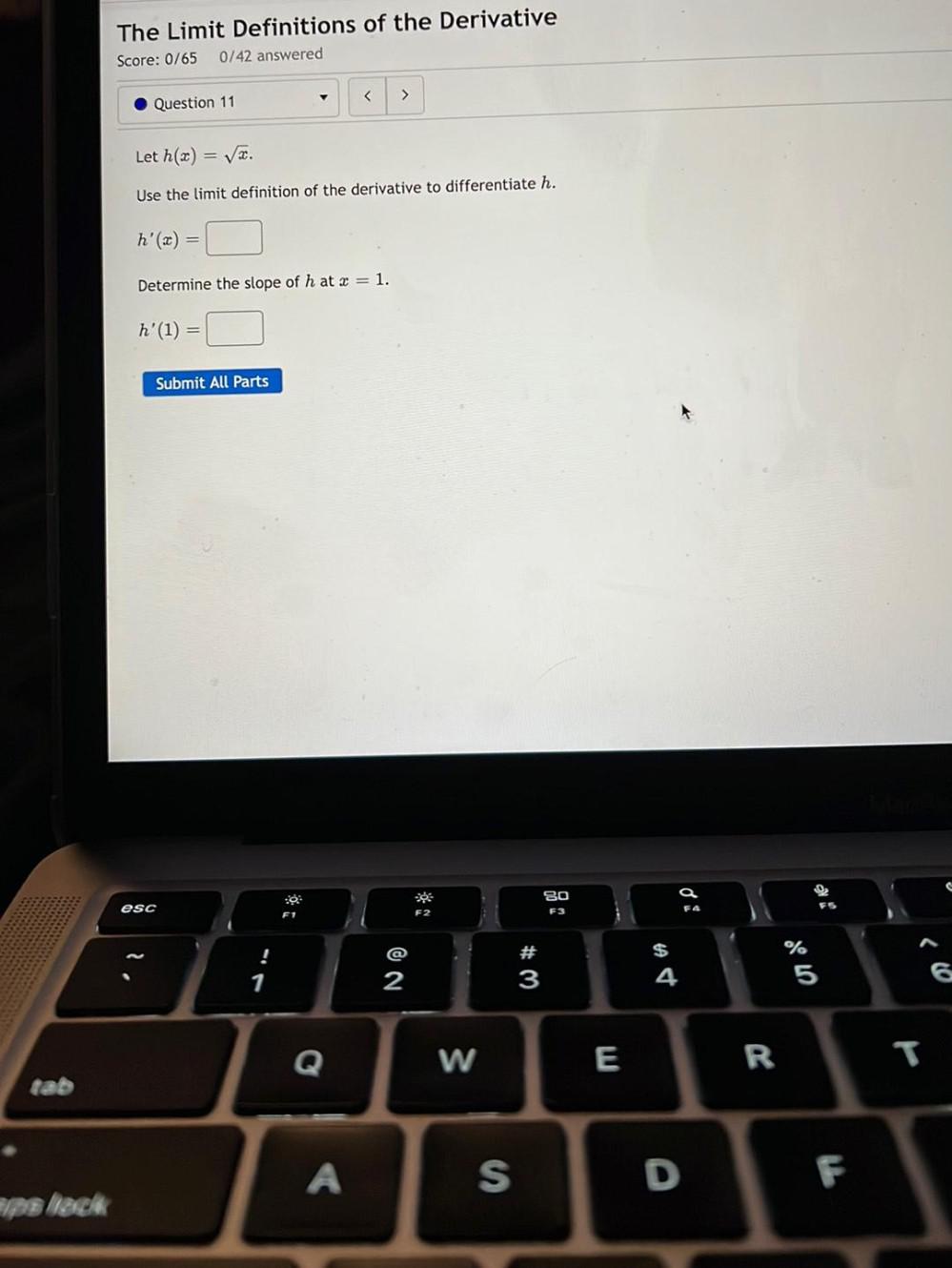
Calculus
DifferentiationLet h(x)=√x.
Use the limit definition of the derivative to differentiate h.
h'(x) = ________
Determine the slope of h at x = 1.
h' (1) = ______
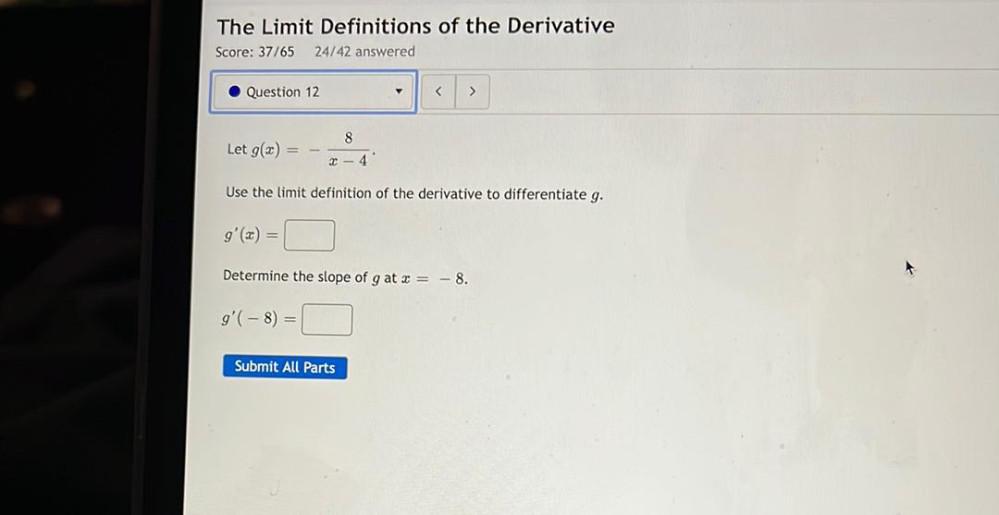
Calculus
DifferentiationThe limit definition of the derivative
Let g(x) = - 8/x-4
Use the limit definition of the derivative to differentiate g.
g'(x) = □
Determine the slope of g at x = -8.
g'(- 8) = □
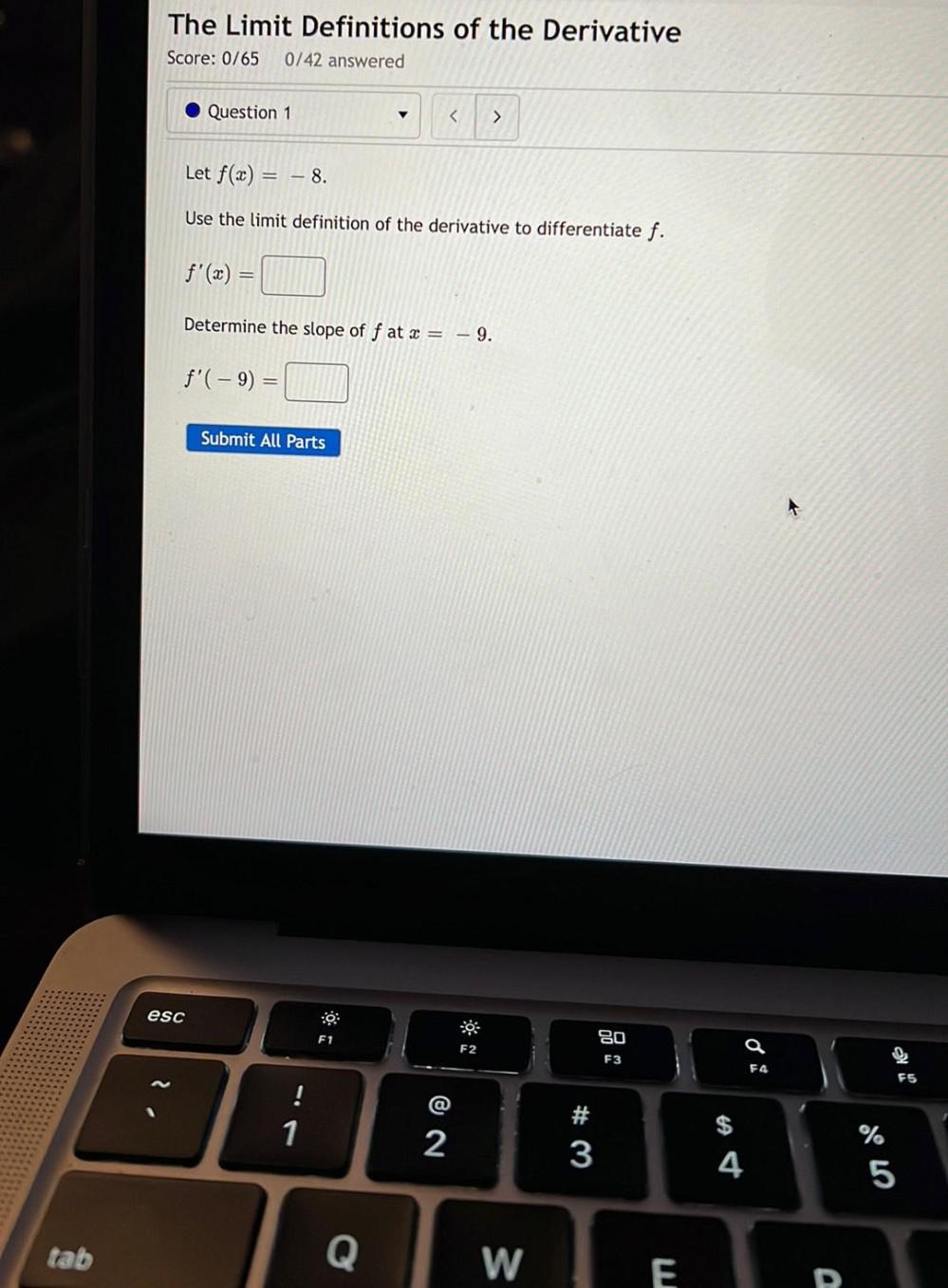
Calculus
DifferentiationLet f(x) = -8.
Use the limit definition of the derivative to differentiate f.
f'(x) = ________________________
Determine the slope of f at x = -9.
f'(- 9) = ________________

Calculus
DifferentiationFit a quadratic function of the form f(t) = c₀ + c₁ t+ c₂ t² to the data points (0,7), (1, 8), (2, –3), (3, −6), using least squares. f(t) =

Calculus
DifferentiationPart 3: Suppose the field has a length of 6,000 feet. Sally buys fencing to enclose it, but has bought 4 feet too much. Rather than throwing away the extra fencing, Sally enclose a slightly larger field by enlarging each side of the field by the same amount, so the fencing encloses the field and a border:
What is the largest animal that could be at point X
and be entirely within the border region, touching
neither the fence nor the field?
a)an ant b)a mouse c)a cat d)a cow e)an elephant
Part 4: Give the average rate of change of the perimeter, if the length increases from 6,000 feet to 7,000 feet:_________
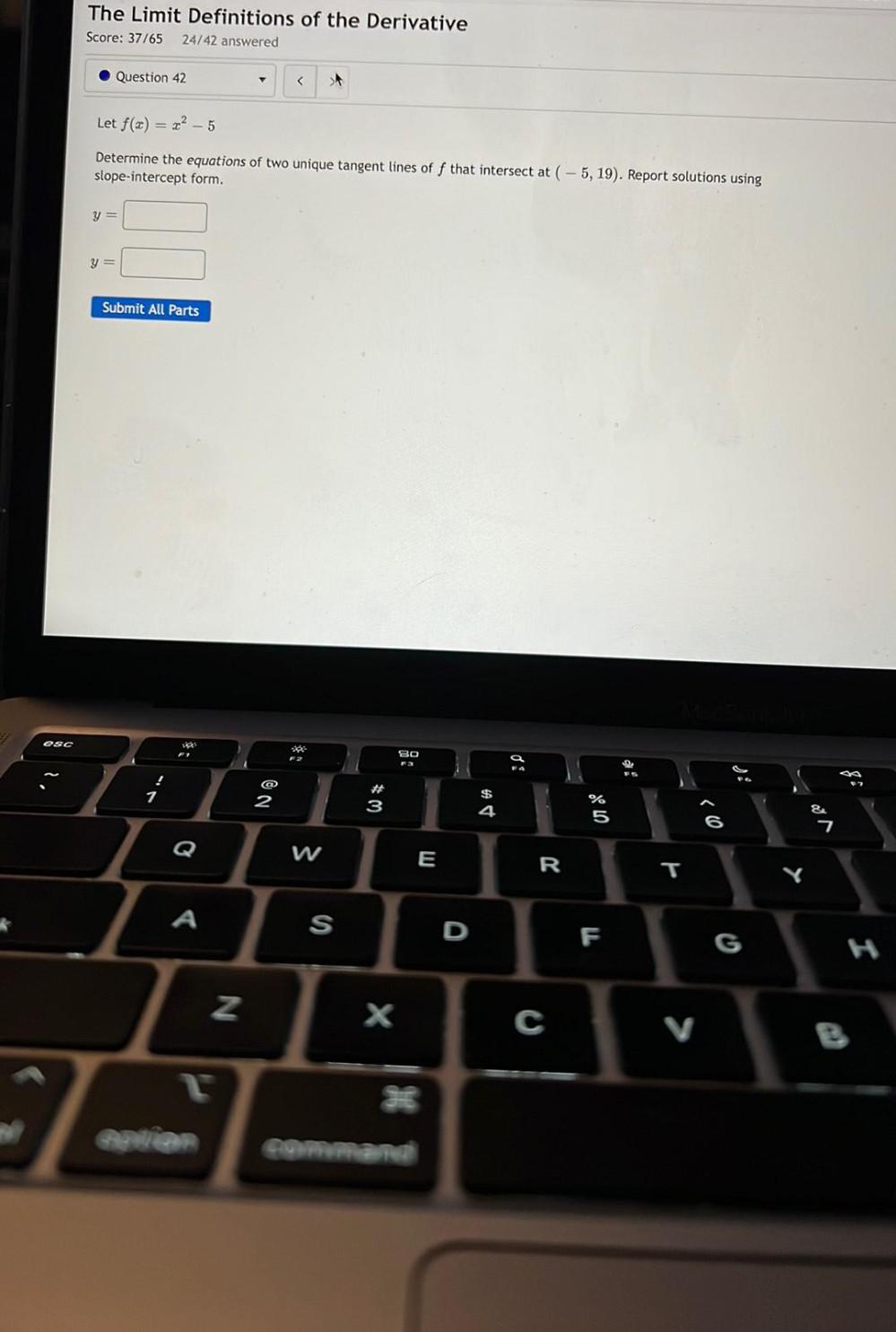
Calculus
Differentiation42)Let f(x)=x²-5
Determine the equations of two unique tangent lines of f that intersect at (-5, 19). Report solutions using
slope-intercept form.
y =
y =
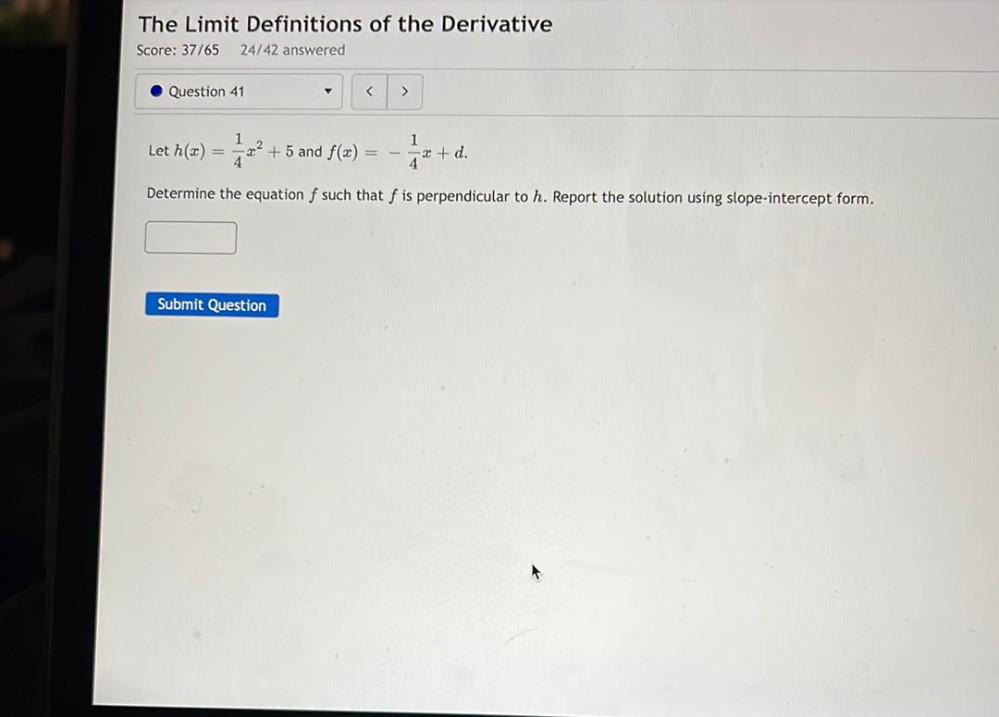
Calculus
DifferentiationLet h(x) = 1/4 x² + 5 and f(x) = -1/4 x + d
Determine the equation f such that f is perpendicular to h. Report the solution using slope-intercept form.
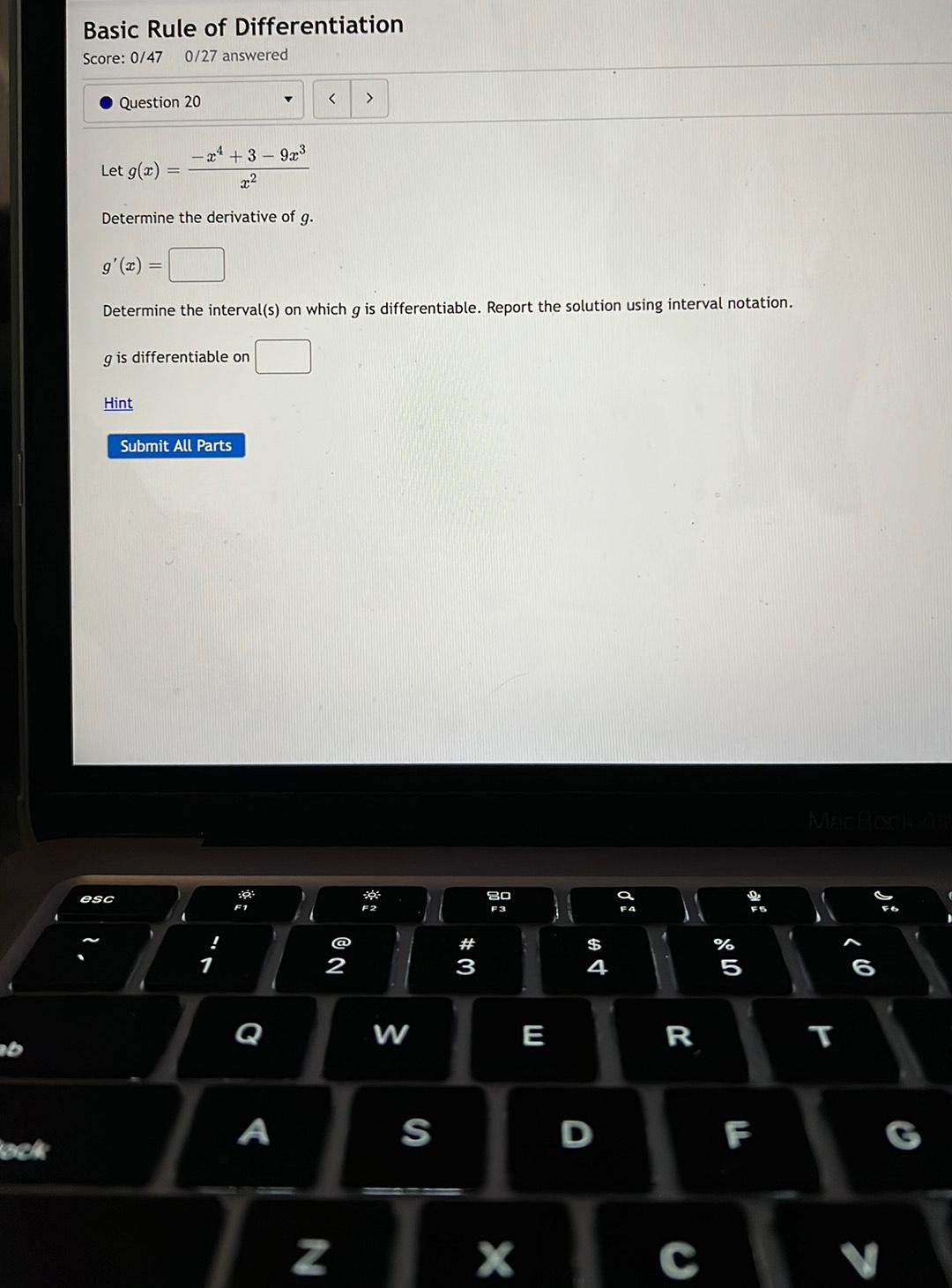
Calculus
DifferentiationLet g(x) = (-x⁴ + 3 - 9x³)/x²
Determine the derivative of g.
g'(x) = _________
Determine the interval(s) on which g is differentiable. Report the solution using interval notation.
g is differentiable on __________
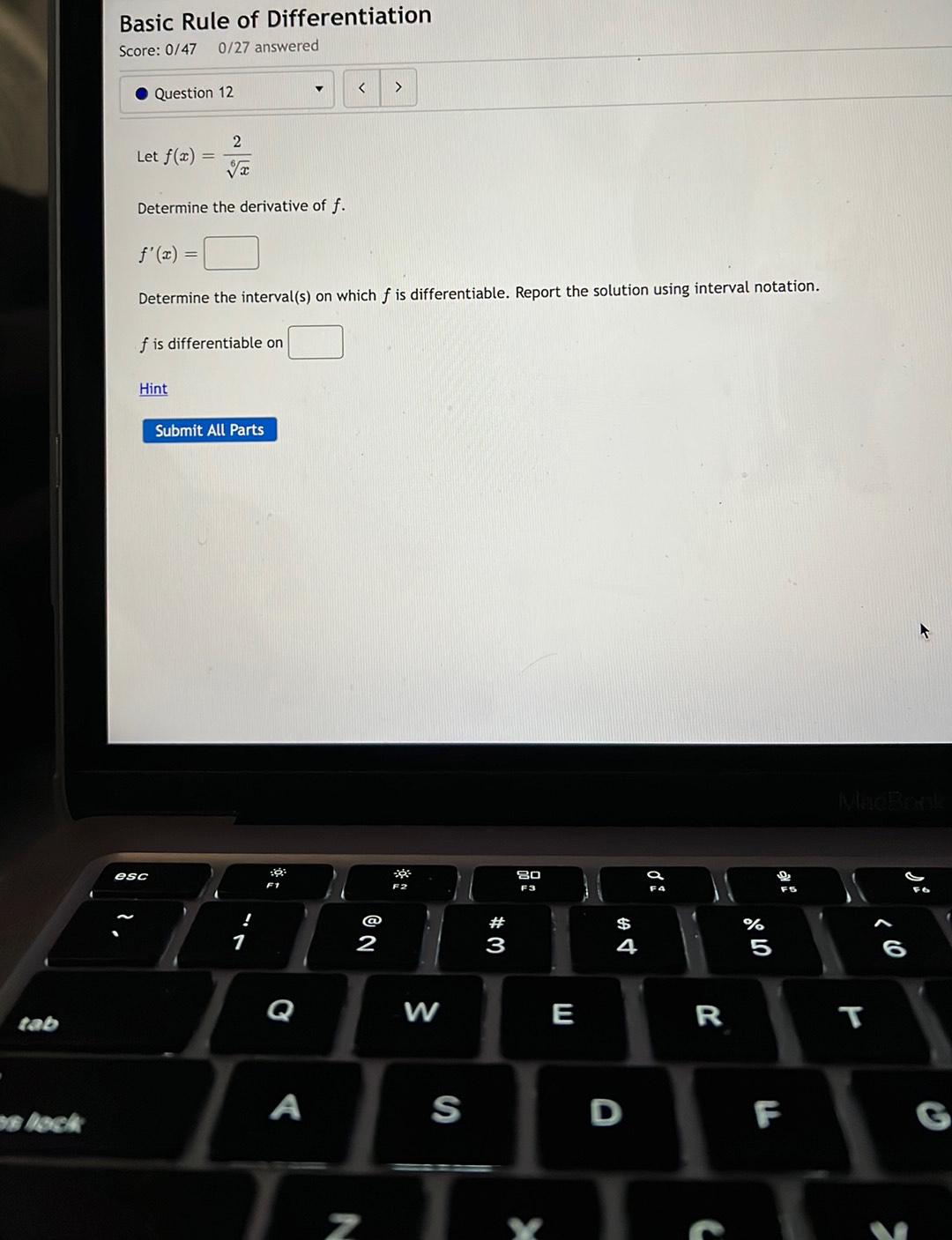
Calculus
DifferentiationLet f(x)=2/x^1/6
Determine the derivative of f. f'(x)=
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
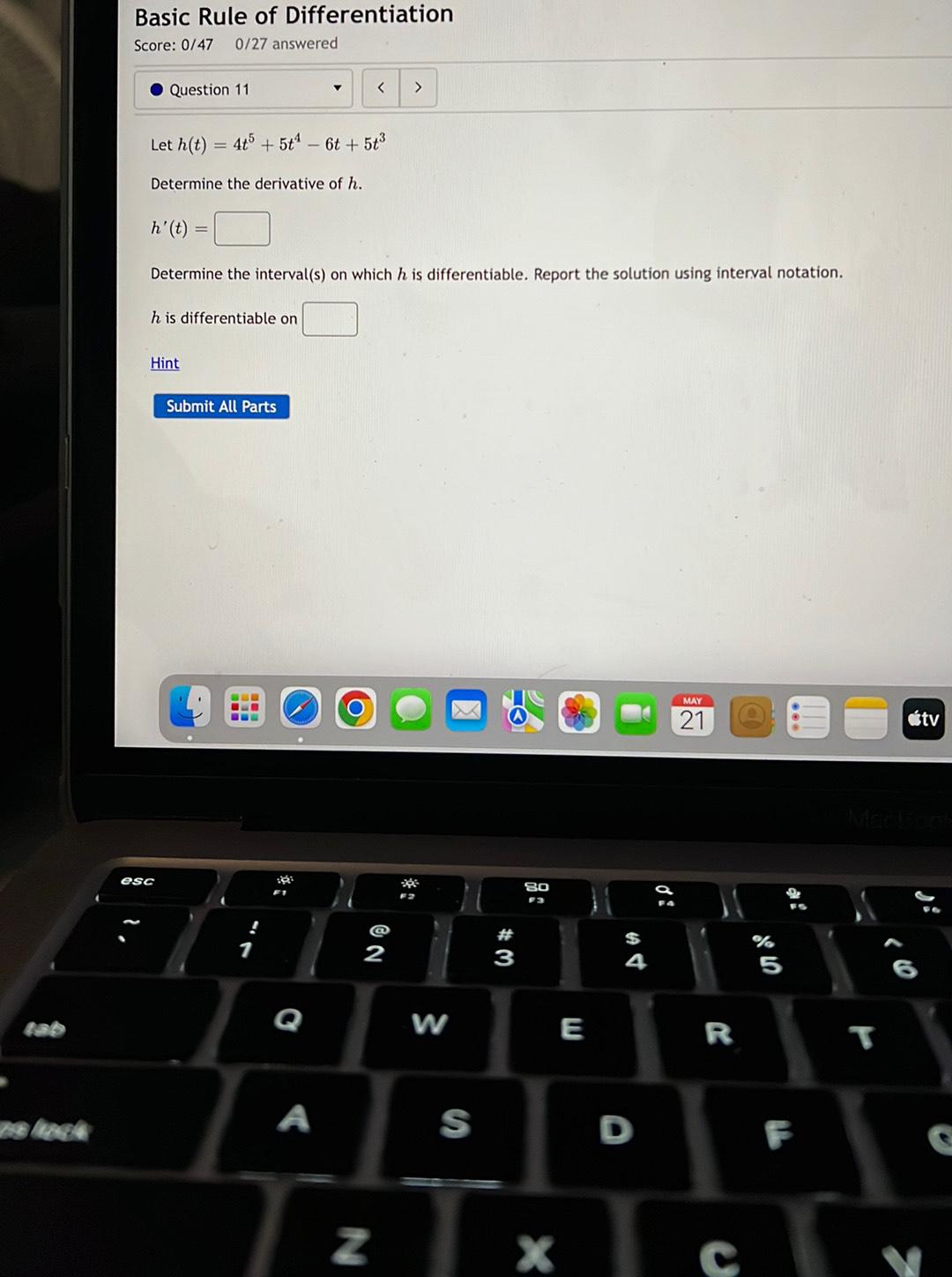
Calculus
DifferentiationLet h(t) 4t^5 + 5t^4 -6t+ 5t³
Determine the derivative of h. h' (t)=
Determine the interval(s) on which h is differentiable. Report the solution using interval notation.
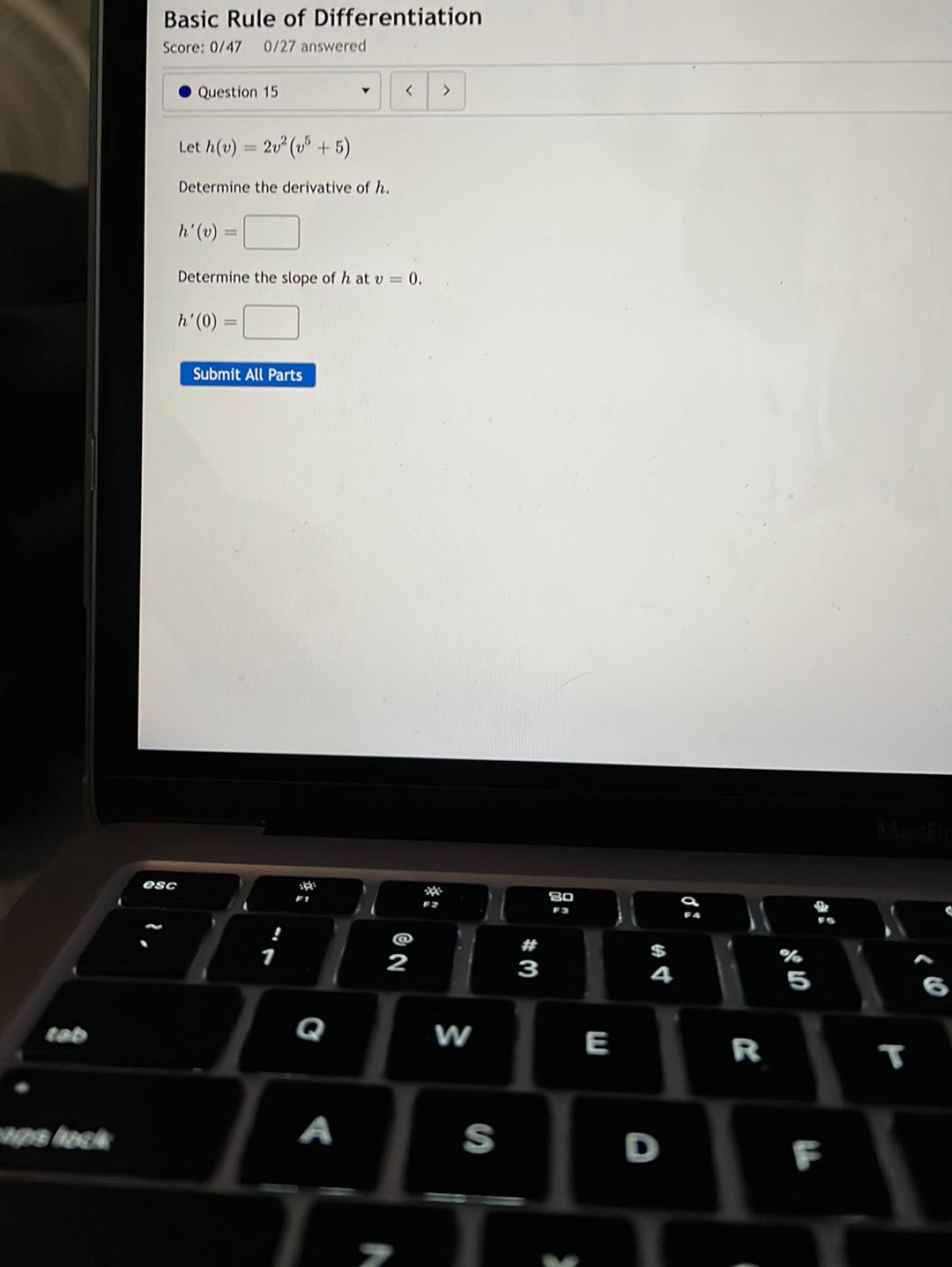
Calculus
DifferentiationLet h(v) = 2v² (v⁵ + 5)
Determine the derivative of h.
h'(v) = ______
Determine the slope of h at v = 0.
h'(0) = _________
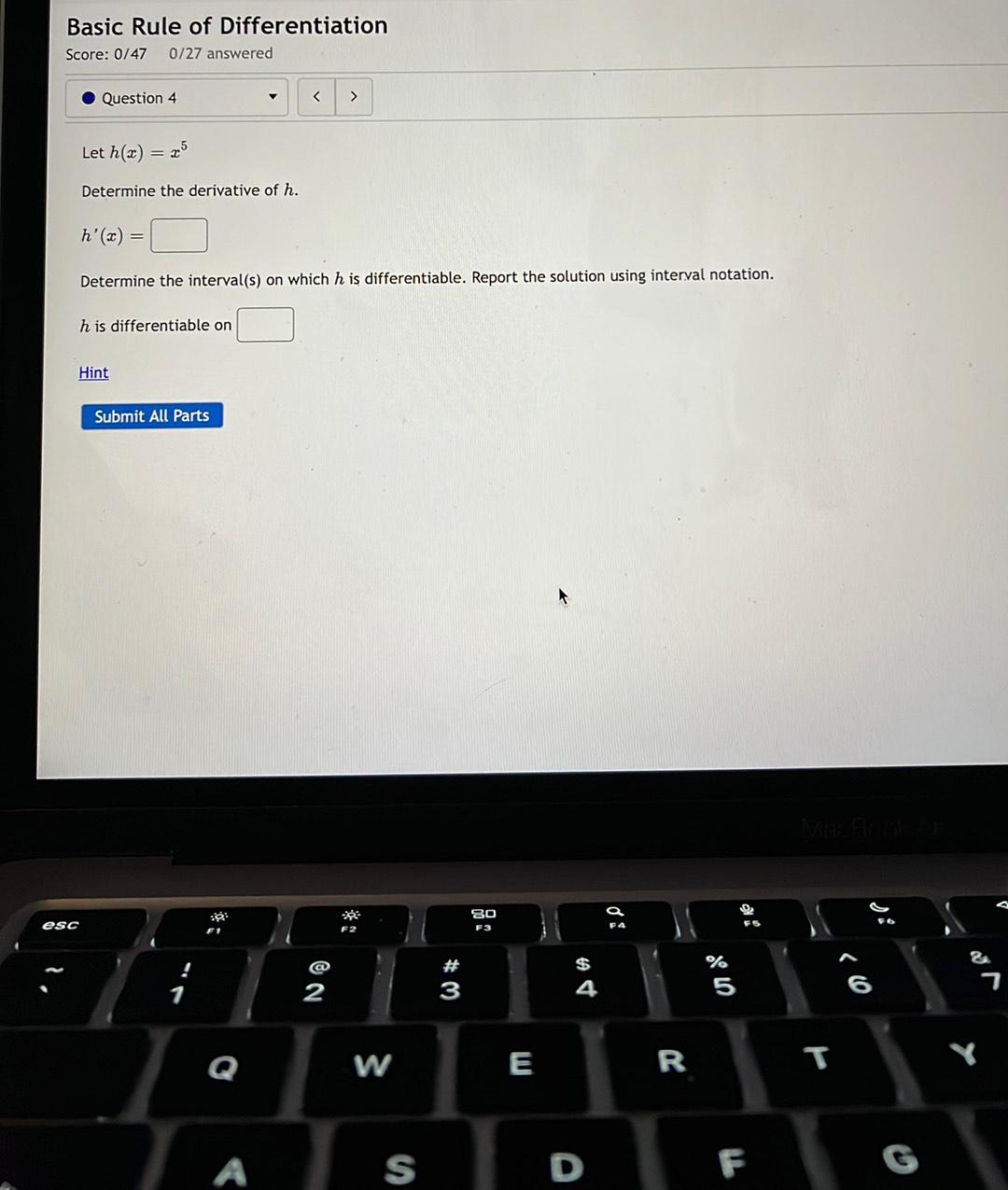
Calculus
DifferentiationLet h(x) =x^5
Determine the derivative of h. h'(x) =
Determine the interval(s) on which h is differentiable. Report the solution using interval notation.
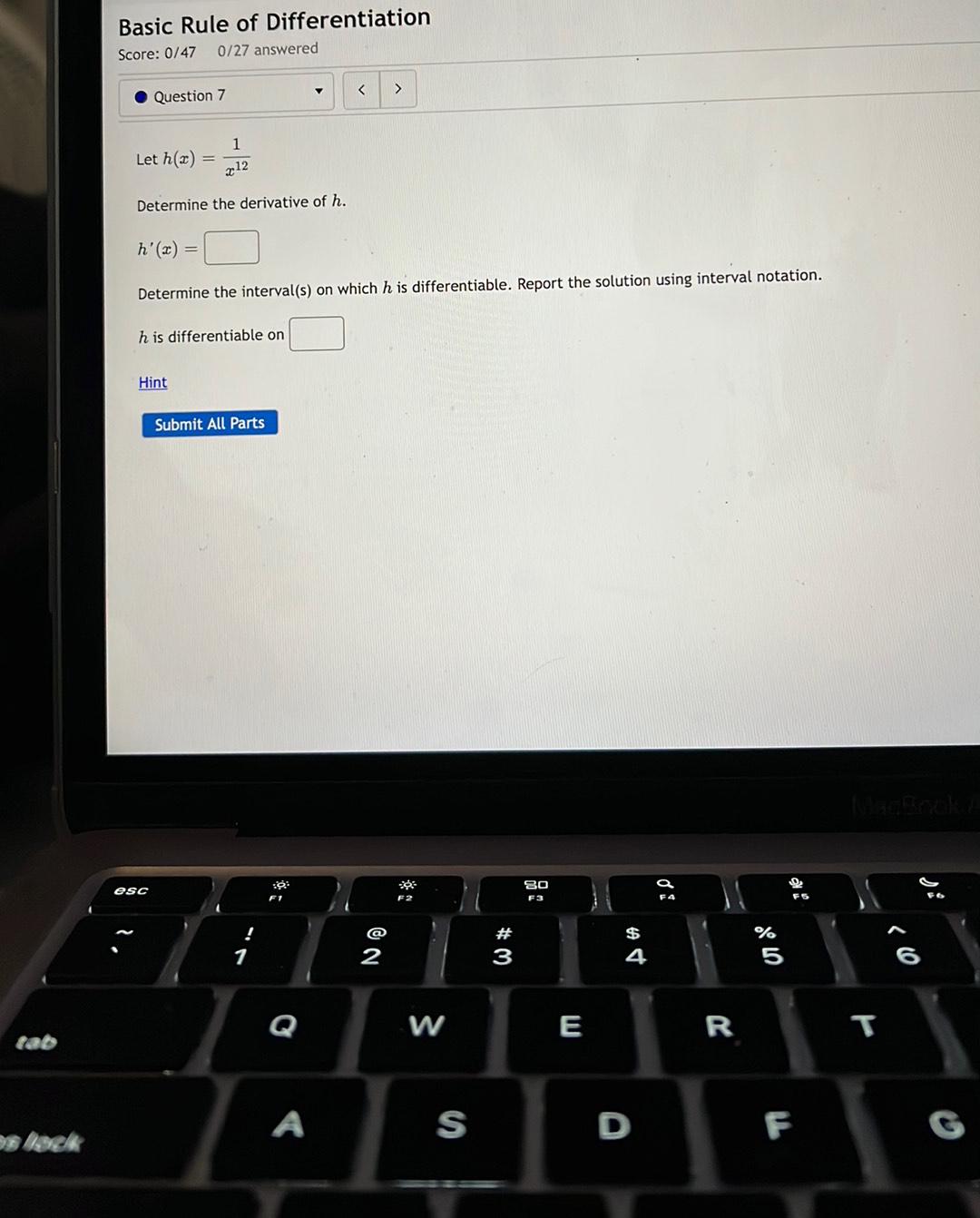
Calculus
DifferentiationLet h(x) =1/x^12
Determine the derivative of h. h'(x) =
Determine the interval(s) on which h is differentiable. Report the solution using interval notation.
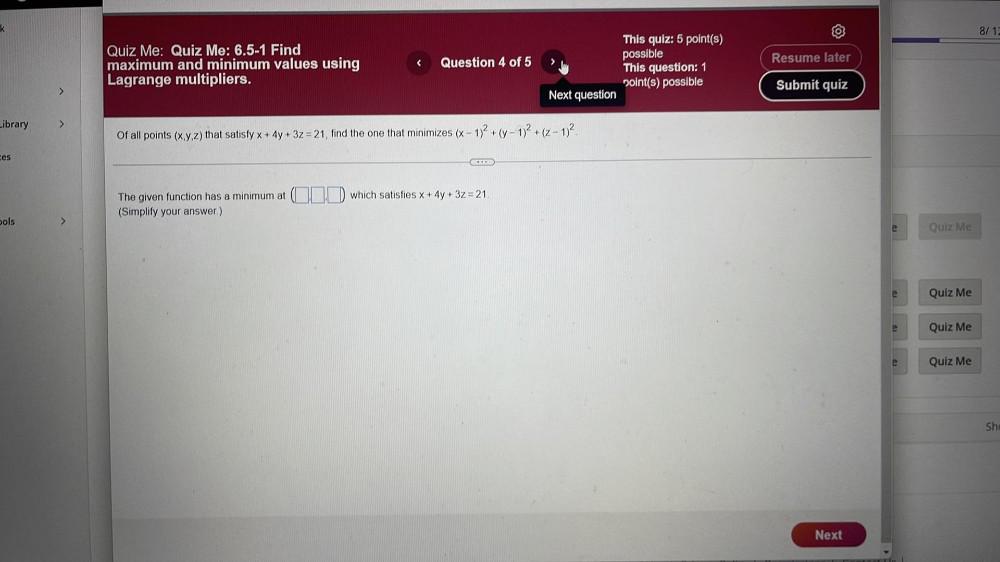
Calculus
Differentiationmaximum and minimum values using Lagrange multipliers.
Of all points (x, y, z) that
x + 4y + 3z=21, find the one that minimizes
(x-1)² + (y-1)² + (z-1)².
The given function has a minimum at (____ ____ ______ )which satisfies
x + 4y + 3z = 21,
![Let g(x)=6/∜x. Determine the derivative of g. g'(x) =[ ].Determine the interval(s) on which g is differentiable. Report the solution using interval notation. g is differentiable on [ ]](https://media.kunduz.com/media/sug-question/raw/79533162-1660165866.3307061.jpeg?w=256)
Calculus
DifferentiationLet g(x)=6/∜x. Determine the derivative of g. g'(x) =[ ].Determine the interval(s) on which g is differentiable. Report the solution using interval notation. g is differentiable on [ ]
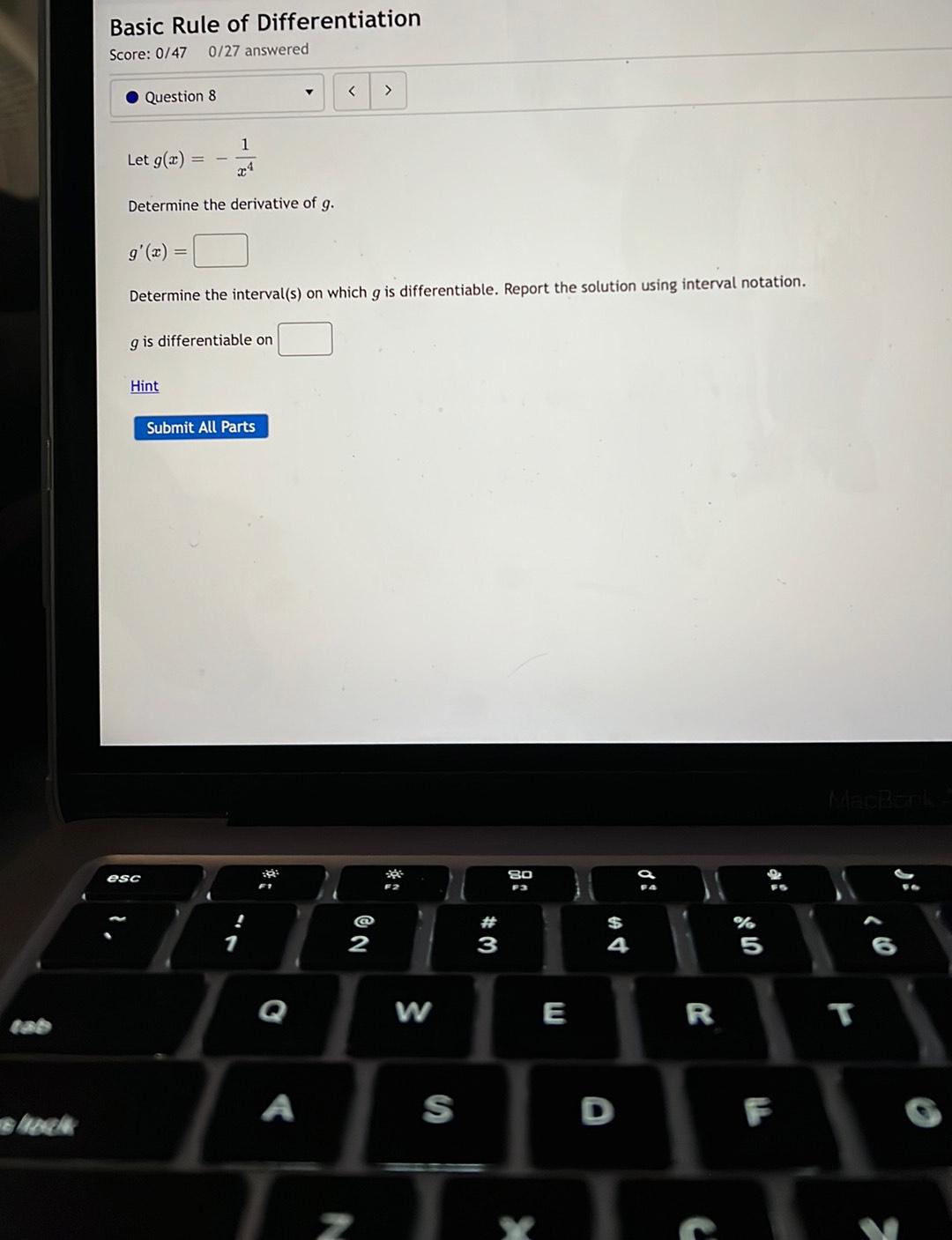
Calculus
DifferentiationLet g(x)=-1/x^4
Determine the derivative of g. g'(x)=
Determine the interval(s) on which g is differentiable. Report the solution using interval notation.
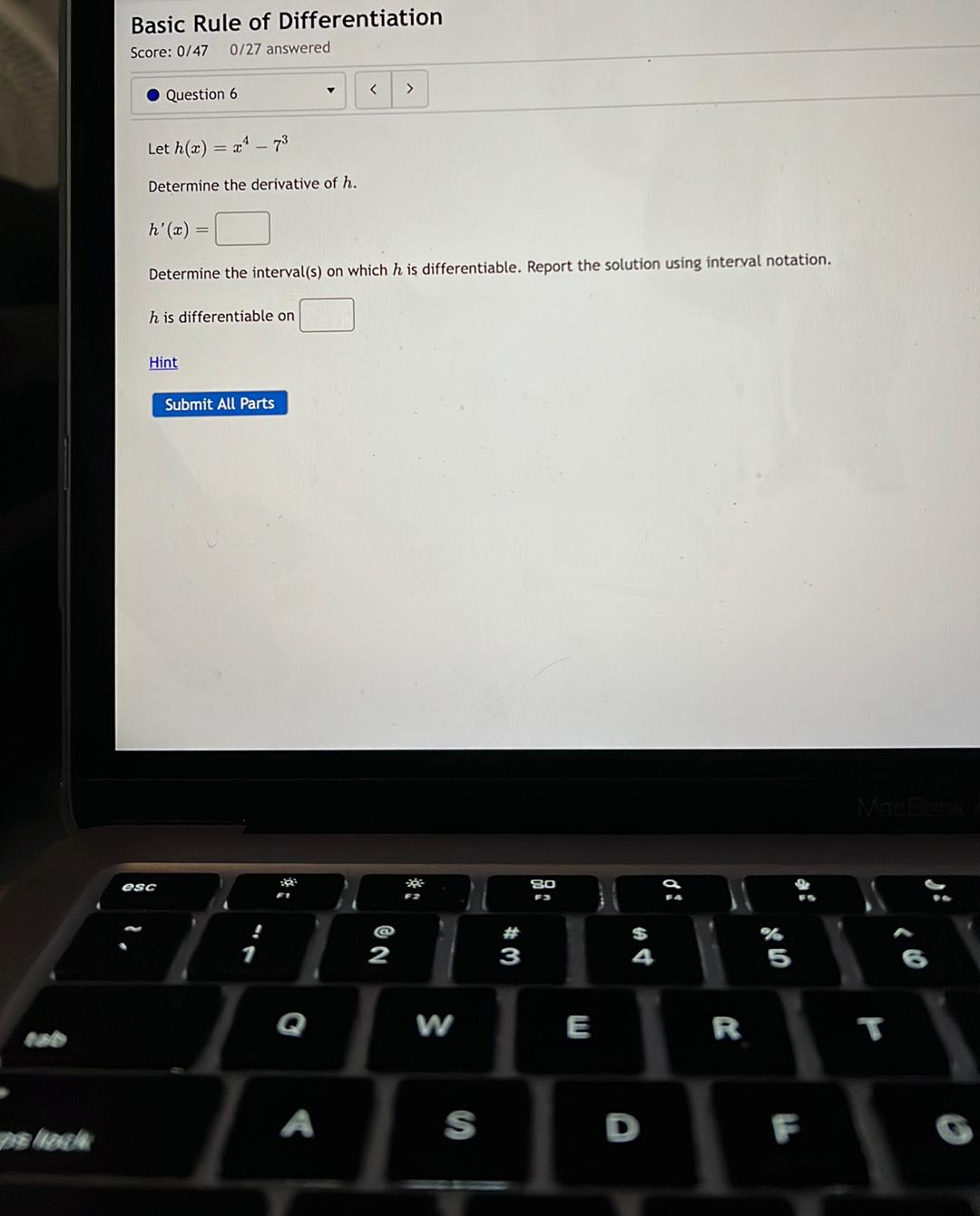
Calculus
DifferentiationLet h(x) = x^4 - 7^3
Determine the derivative of h. h'(x) =
Determine the interval(s) on which h is differentiable. Report the solution using interval notation.
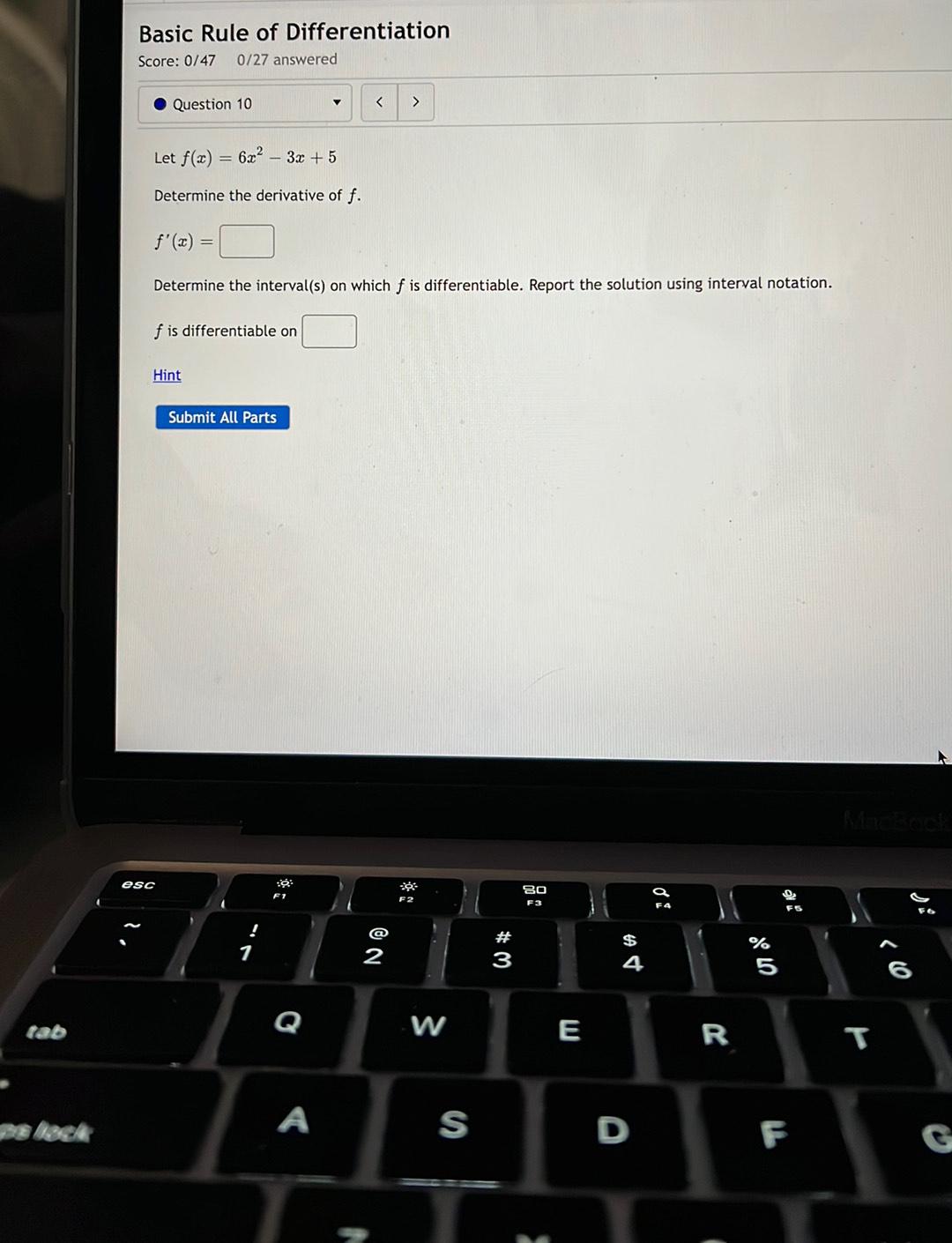
Calculus
DifferentiationLet f(x) = 6x² - 3x + 5
Determine the derivative of f.
f'(x) = _________
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
f is differentiable on _______
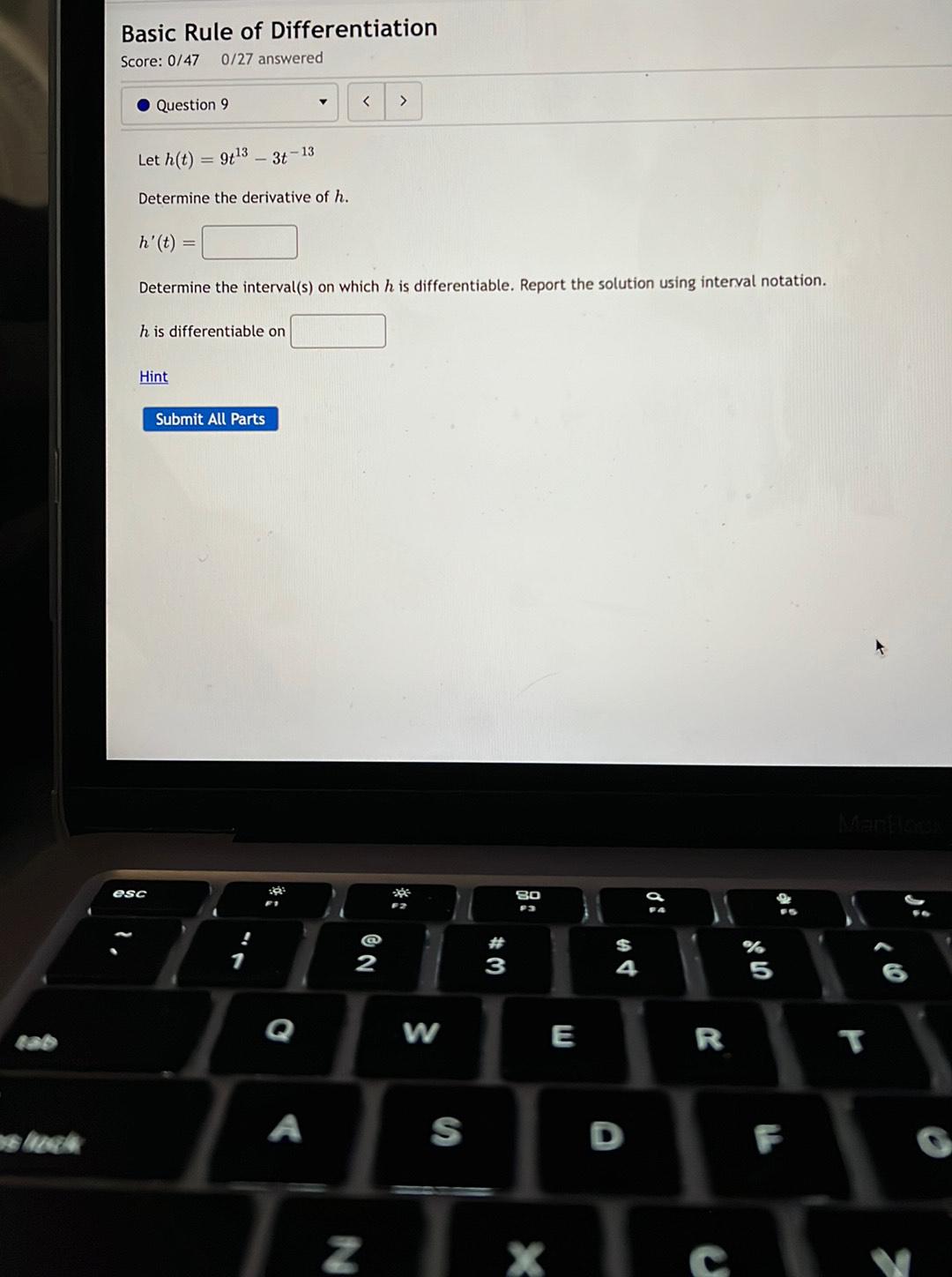
Calculus
Differentiationlet h(t)=9t^13 -3t^-13
Determine the derivative of h. h' (t)=
Determine the interval(s) on which h is differentiable. Report the solution using interval notation.
Calculus
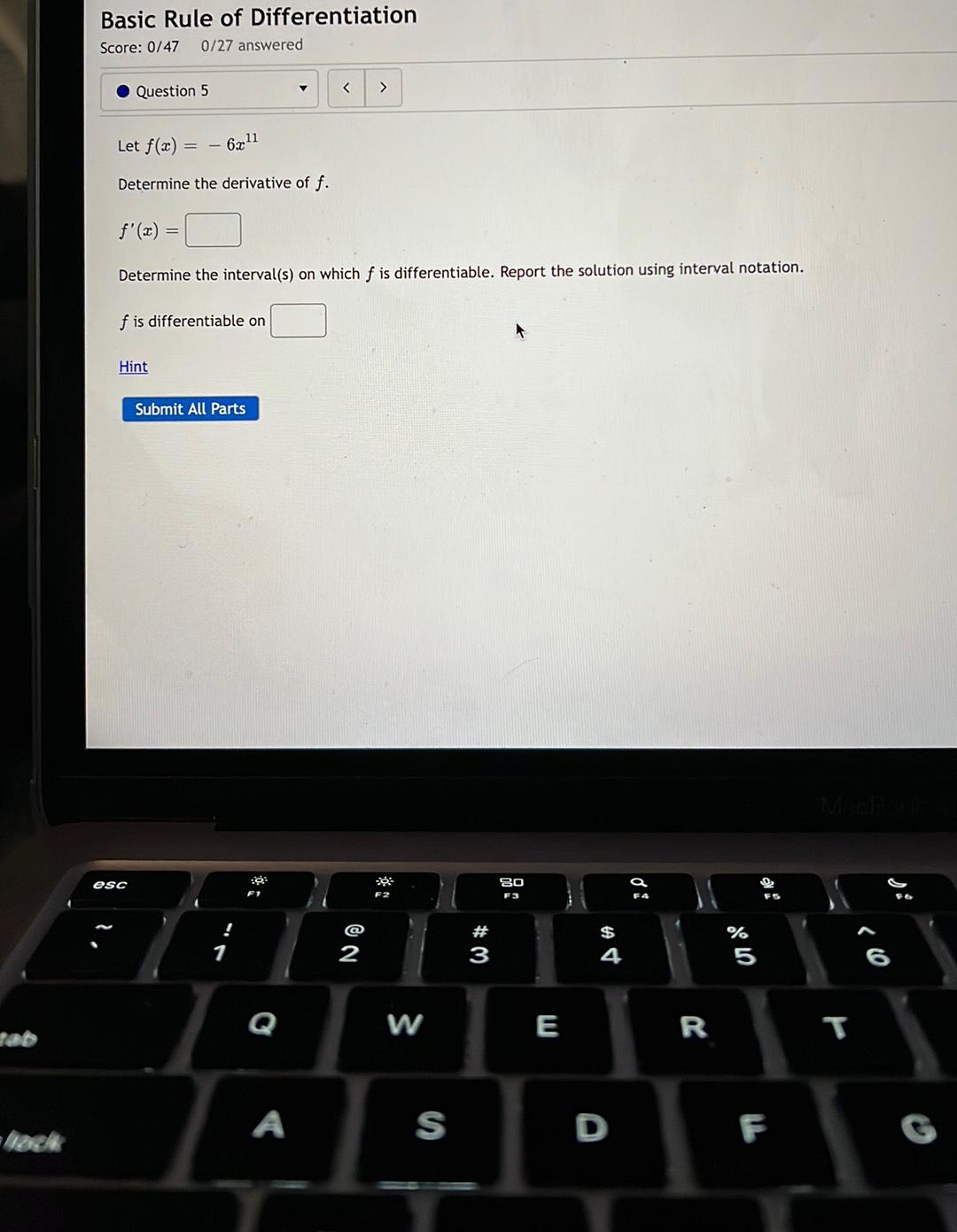
DifferentiationLet f(x)=- 6x^11
Determine the derivative of f.f'(x)=
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
Calculus
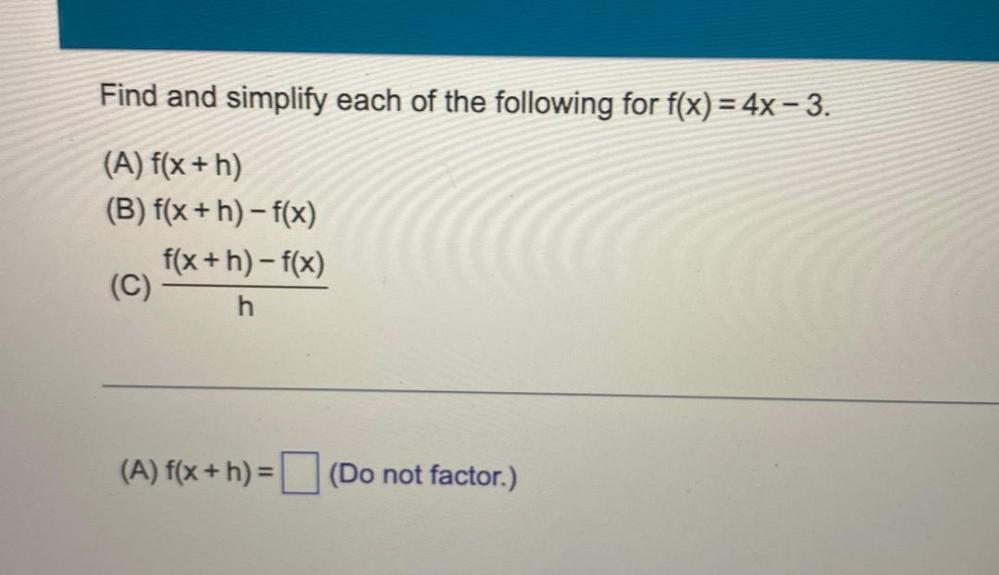
DifferentiationFind and simplify each of the following for f(x) = 4x-3.
(A) f(x + h)
(B) f(x+h)-f(x)
(C)(f(x+h)-f(x))/h
(Do not factor.)
Calculus
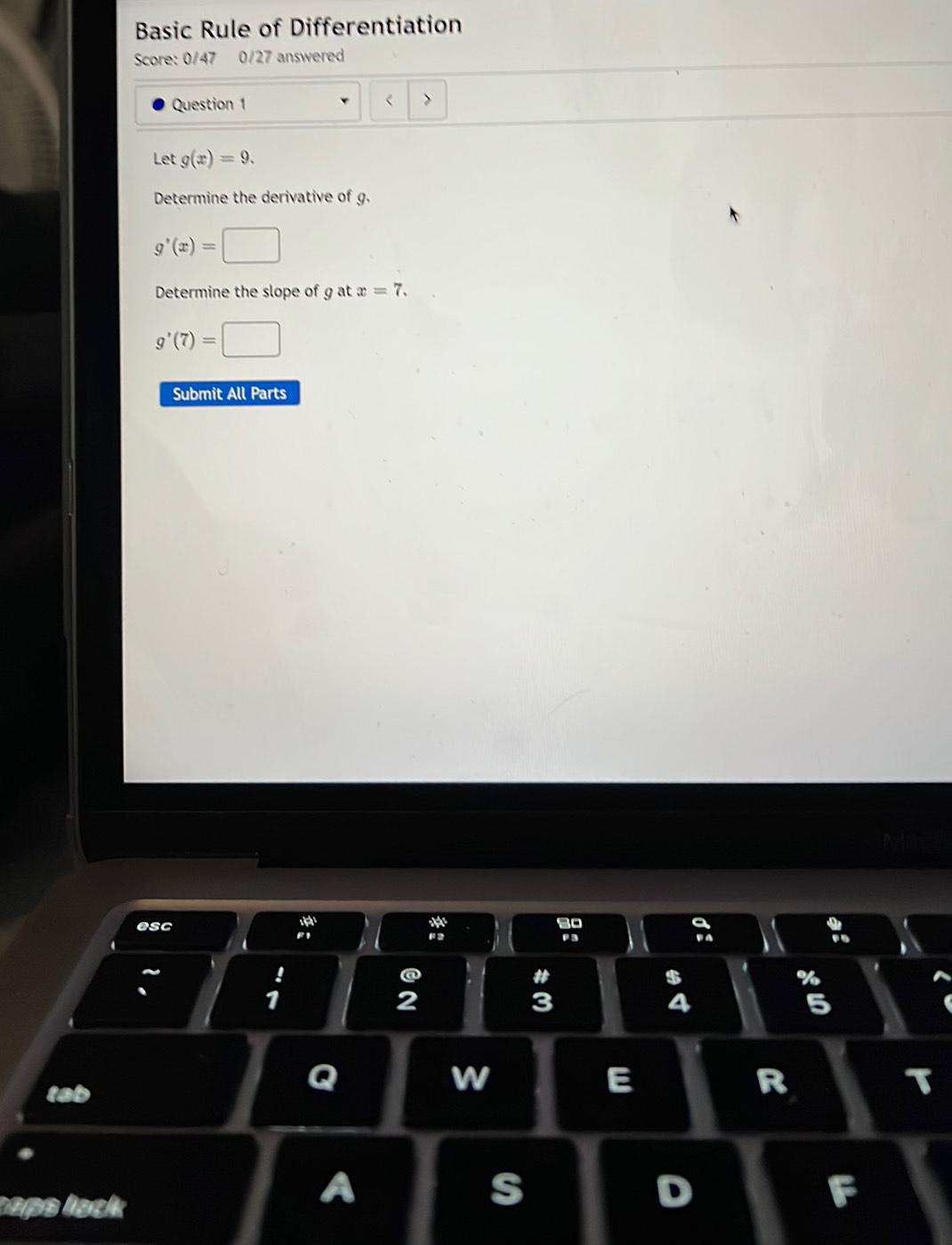
DifferentiationLet g(x) = 9.
Determine the derivative of g.
Determine the slope of g at X = 7. g'(7)=
Calculus
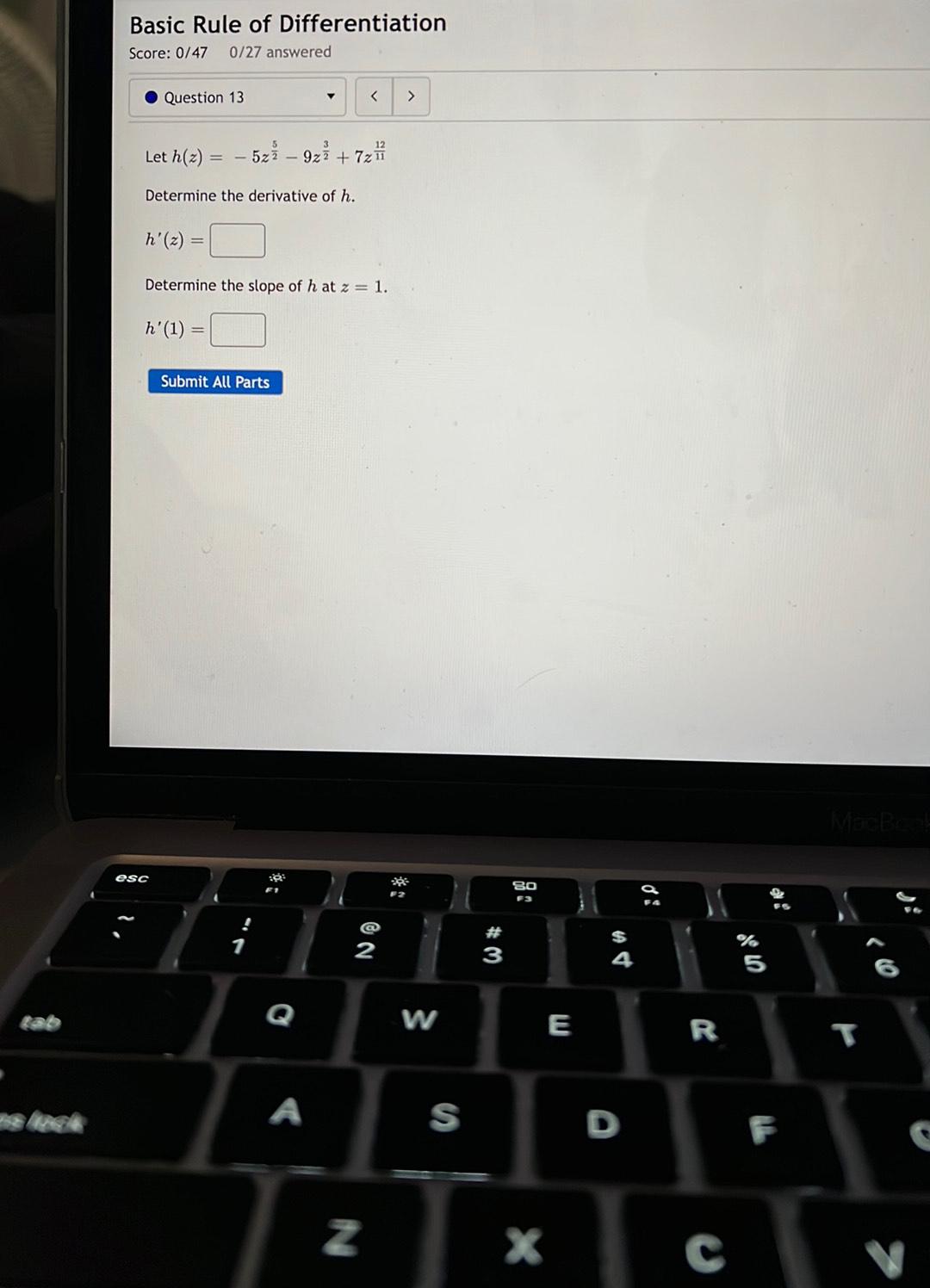
DifferentiationLet h(z) = -5z(⁵/²) - 9z(³/²) + 7z(¹²/¹¹)
Determine the derivative of h.
h'(z) = ______
Determine the slope of h at z = 1.
h' (1) = ______
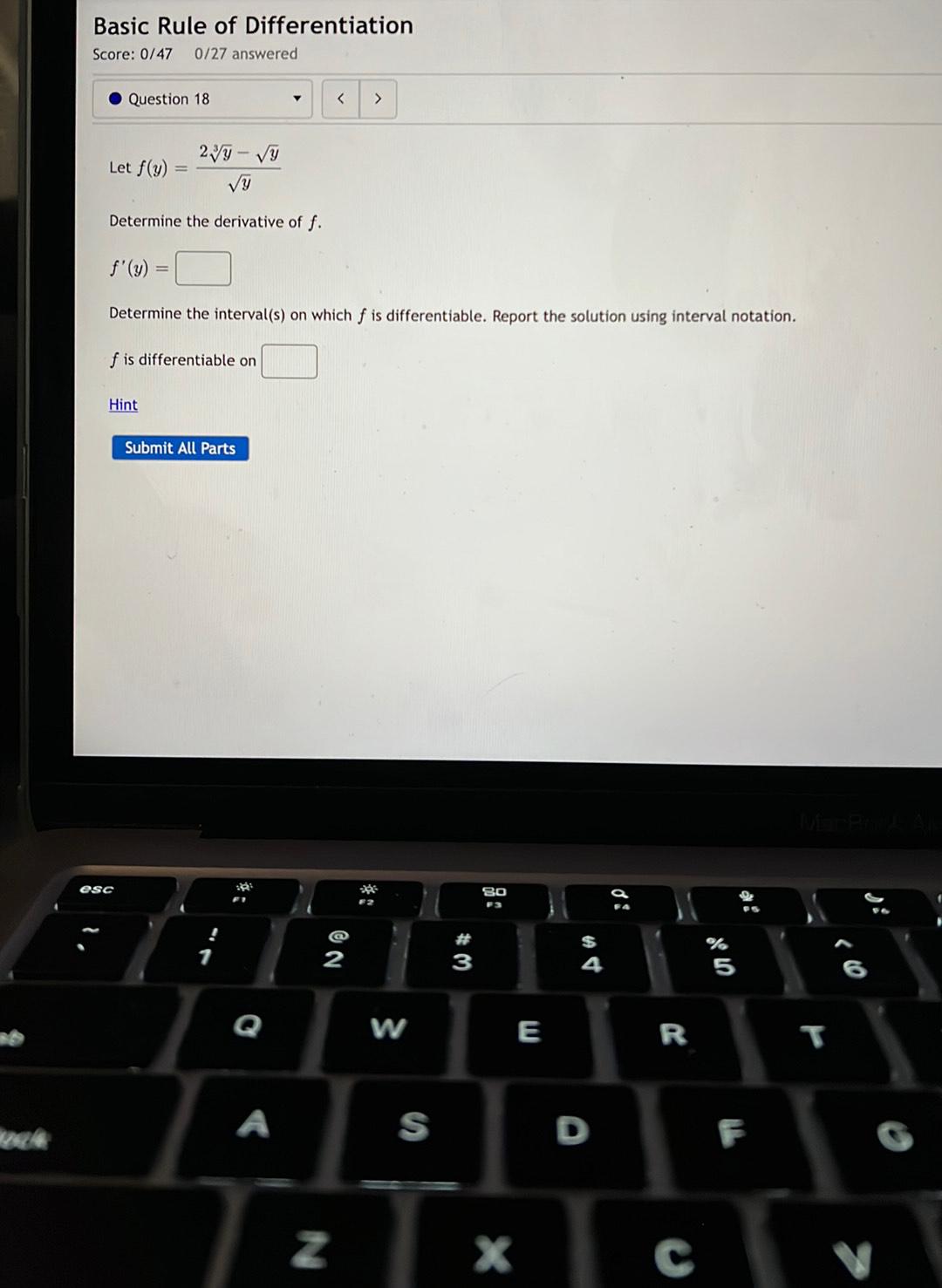
Calculus
DifferentiationLet f(w)=(-5w-4w^4 +3)/w^1/3
Determine the derivative of f. f'(w)=
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
f is differentiable on_______
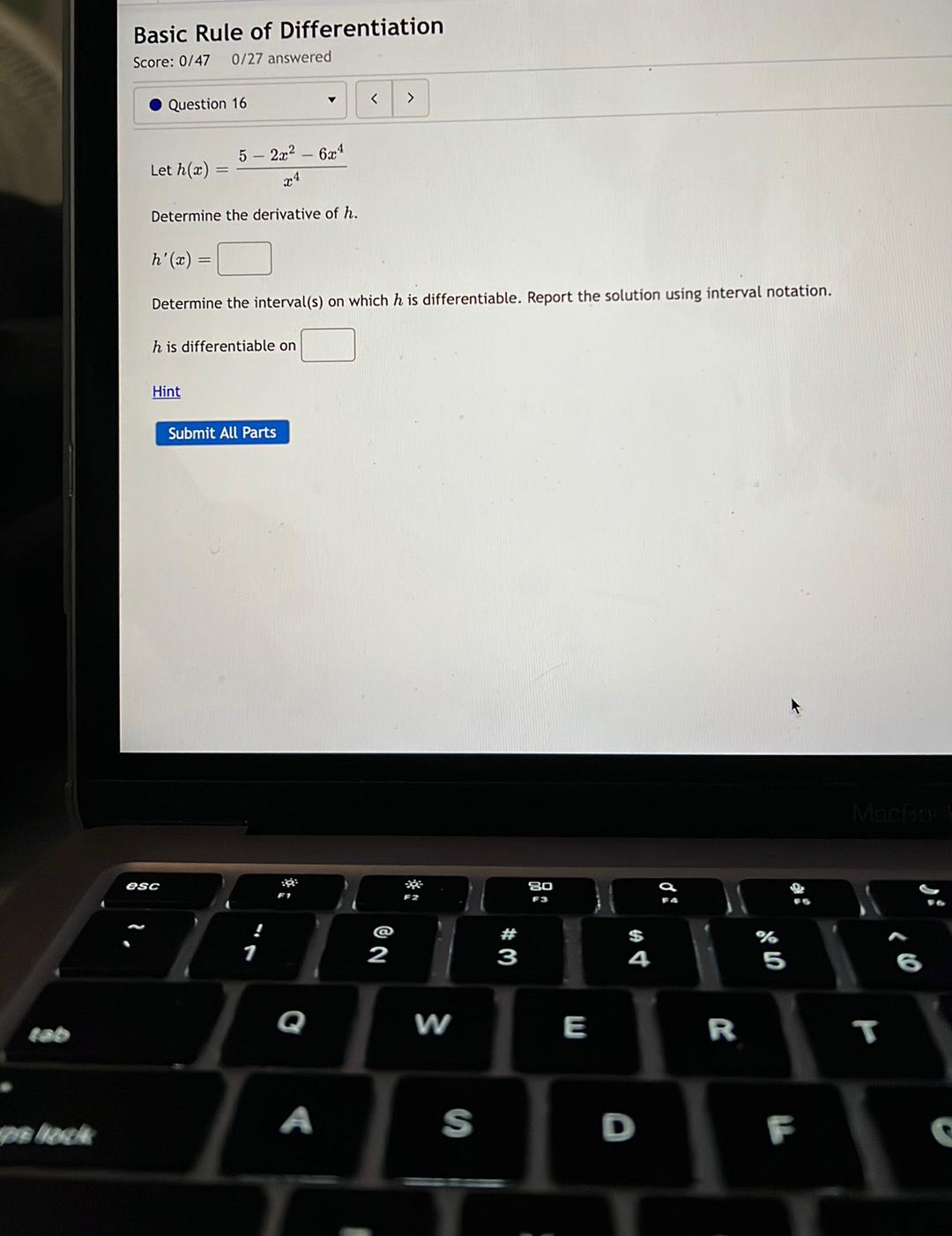
Calculus
DifferentiationLet h(x) = (5 - 2x² - 6x⁴)/x⁴
Determine the derivative of h.
h'(x) = ________
Determine the interval(s) on which h is differentiable. Report the solution using interval notation.
h is differentiable on ____
![let g(x)=1/x⁶. Determine the derivative of g. g'(x) =[? ].Determine the interval(s) on which g is differentiable. Report the solution using interval notation. g is differentiable on[ ?]](https://media.kunduz.com/media/sug-question/raw/79533153-1660165075.396988.jpeg?w=256)
Calculus
Differentiationlet g(x)=1/x⁶. Determine the derivative of g. g'(x) =[? ].Determine the interval(s) on which g is differentiable. Report the solution using interval notation. g is differentiable on[ ?]
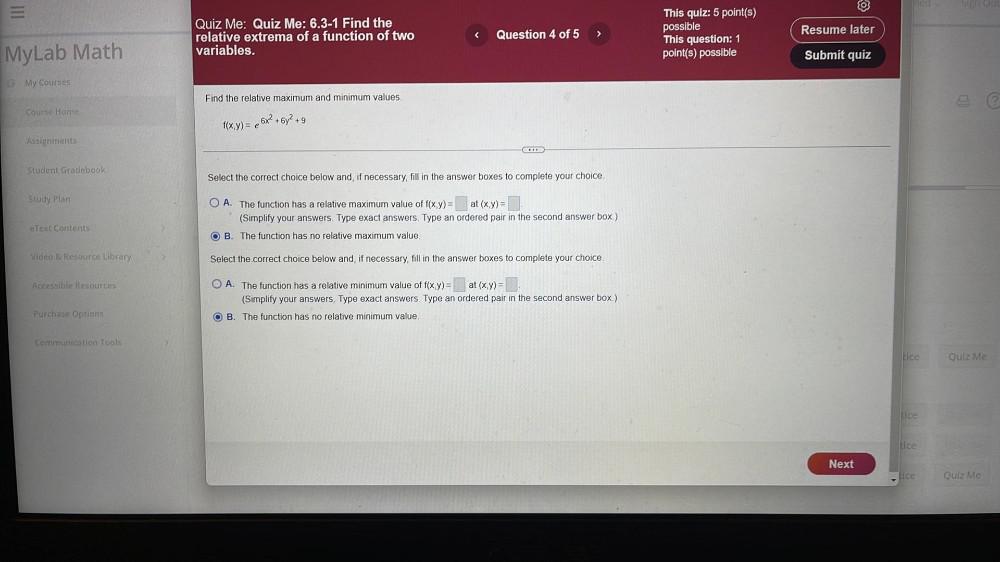
Calculus
DifferentiationFind the relative maximum and minimum values.
f(x,y)= e^(6x² +6y² +9)
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative maximum value of f(x,y)= at (x,y) =______
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative maximum value.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative minimum value of f(x,y) = at (x,y) =_____
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative minimum value.
![Let g(v)=-v^(12/5) + (2)v^(7/3)-(7)v^(9/8)
Determine the derivative of g. g'(v)=[?]
Determine the slope of g at v = 1. g'(1)=[?]](https://media.kunduz.com/media/sug-question/raw/79533142-1660164797.4980233.jpeg?w=256)
Calculus
DifferentiationLet g(v)=-v^(12/5) + (2)v^(7/3)-(7)v^(9/8)
Determine the derivative of g. g'(v)=[?]
Determine the slope of g at v = 1. g'(1)=[?]
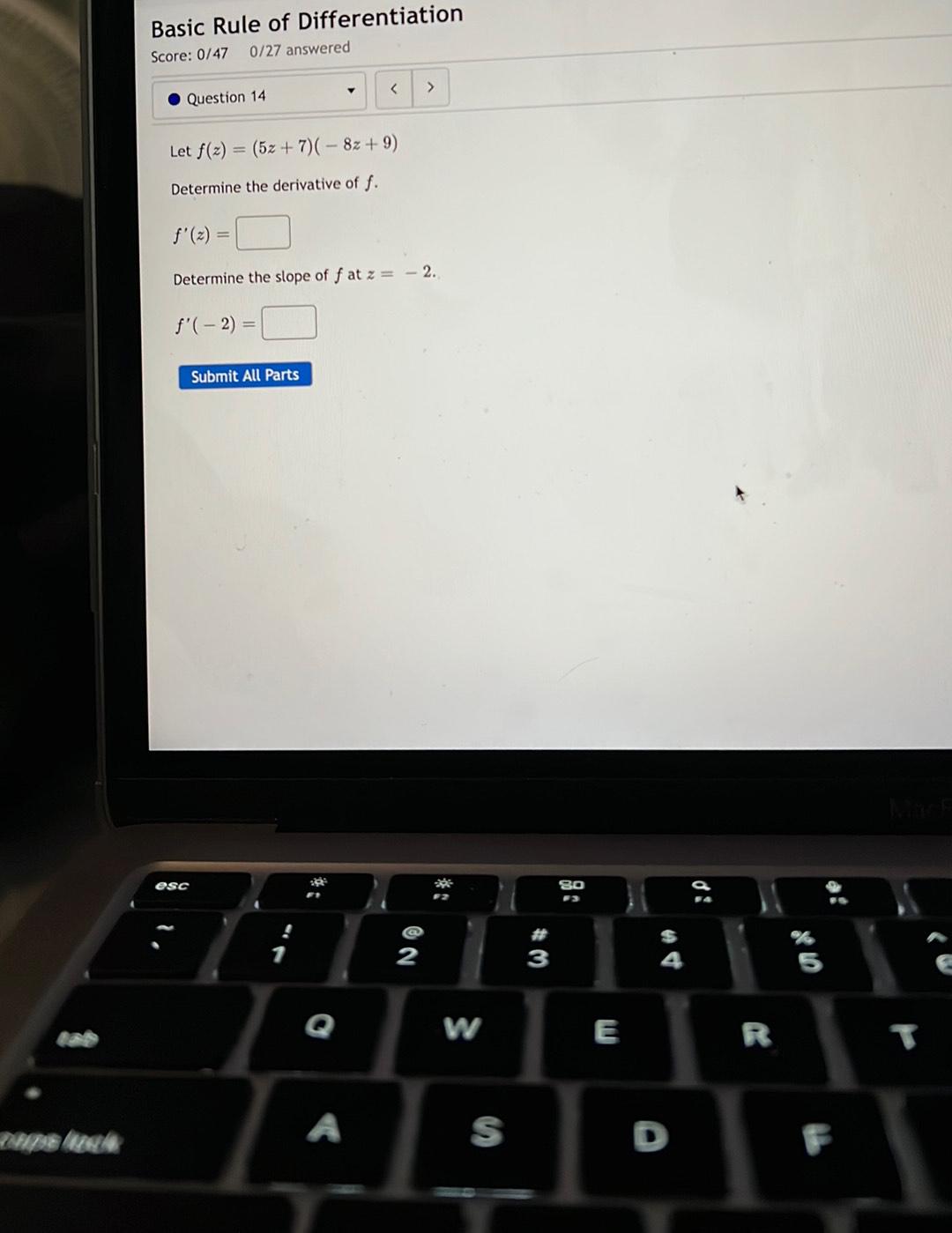
Calculus
DifferentiationLet f(z) = (5z + 7)(-8z +9)
a)Determine the derivative of f. f'(z)=
b)Determine the slope of f at z = -2.
f'(-2)=

Calculus
Differentiationfind the Taylor series of each function at the indicated number. Give the interval of convergence for each series.
f(x)=x² In (1 + x/2) ;x=0
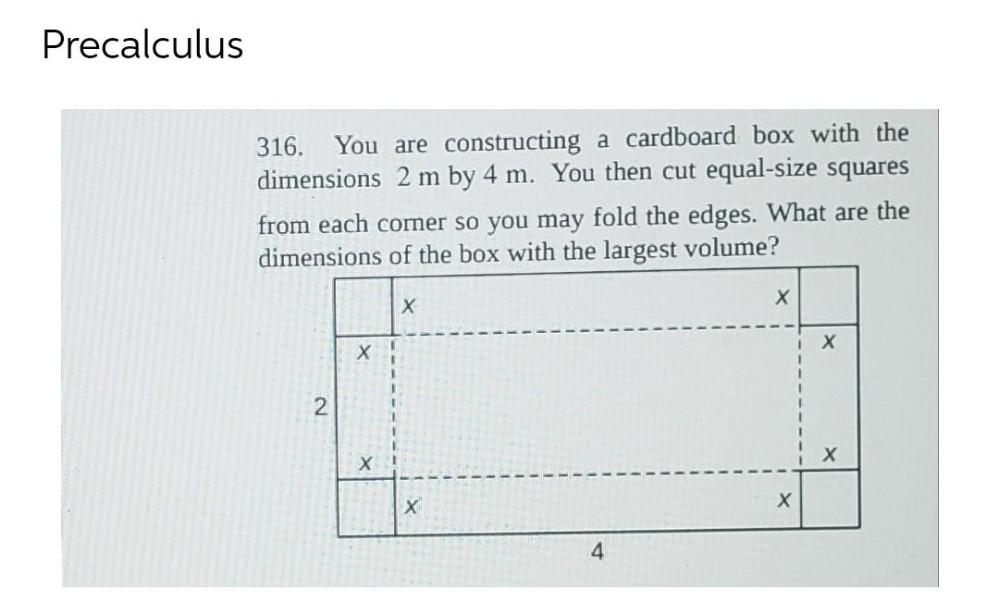
Calculus
DifferentiationYou are constructing a cardboard box with the dimensions 2m by 4m. You then cut equal-size squares from each corner so you may fold the edges. What are the dimensions of the box with the largest volume?

Calculus
DifferentiationYou want to enclose a rectangular region with 450 feet of fencing. Express A(w), the area of the region as a function of its with.
A(w)=_________
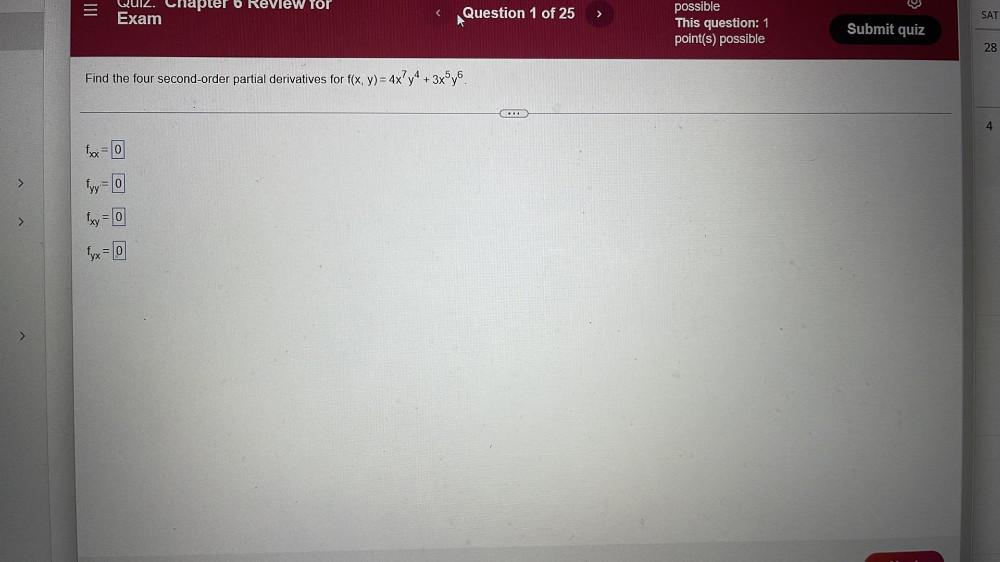
Calculus
DifferentiationFind the four second-order partial derivatives for f(x,y)=4x^(7).y^(4)+3x^(5).y^(6).
fxx = ___
fyy= ___
fxy = ___
fyx = ___

Calculus
DifferentiationThis problem has two parts.
Part 1: In 2069, a virus begins in Boston and spreads in such that the number N of people infected grows exponentially with time t. The table below shows how many days it takes from initial outbreak to have various numbers of cases.
N = # of 1 2 3
cases million million million
t=# of days 108 157 186
How many days until the Boston virus infects five million people? ______
How many days until there are ten million people infected by the Boston virus?______
Part 2: Enter here (using math notation or by attaching
in an image) an explanation of your answers.

Calculus
DifferentiationConsider the curve parameterized by: x =2t^3/2 - 1 and y = 5t.
(a.) Find an equation for the line tangent to the curve at t = 1.
![Consider the function f(x) = 2x² + 3x - 4 on the closed interval [-2, 1].
Find the exact value of the slope of the secant line connecting
(-2, f(-2)) and (1, f(1)).
m =___________
By the Mean Value Theorem, there exists c in (-2, 1) so that m = f'(c). Find all values of such c in (-2, 1). Enter exact values. If there is more than one solution, separate them by a comma.
c=___________](https://media.kunduz.com/media/sug-question/raw/80067126-1660162193.32958.jpeg?w=256)
Calculus
DifferentiationConsider the function f(x) = 2x² + 3x - 4 on the closed interval [-2, 1].
Find the exact value of the slope of the secant line connecting
(-2, f(-2)) and (1, f(1)).
m =___________
By the Mean Value Theorem, there exists c in (-2, 1) so that m = f'(c). Find all values of such c in (-2, 1). Enter exact values. If there is more than one solution, separate them by a comma.
c=___________
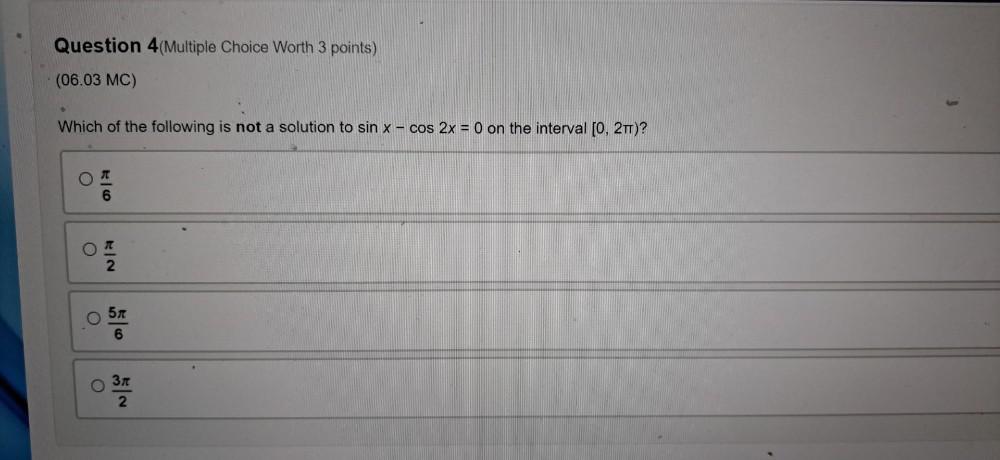
Calculus
DifferentiationWhich of the following is not a solution to sin x-cos 2x = 0 on the interval [0, 2π)?
(a)π/6
(b)π/2
(c)5π/6
(d)3π/2
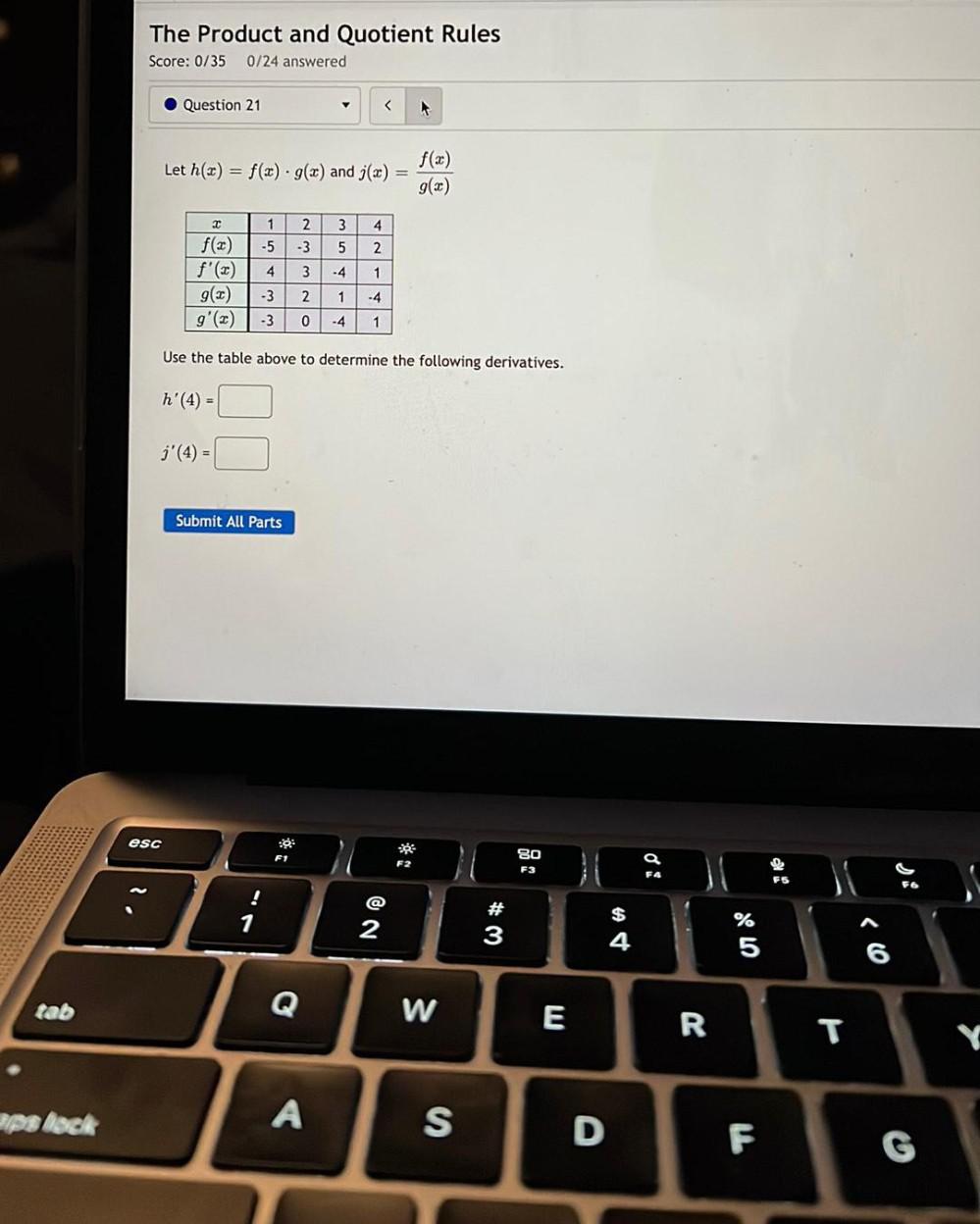
Calculus
DifferentiationLet h(x) = f(x) · g(x) and j(x) = f(x)/g(x)
x 1 2 3 4
f(x) -5 -3 5 2
f'(x) 4 3 -4 1
g(x) -3 2 1 -4
g'(x) -3 0 -4 1
Use the table above to determine the following derivatives.
h' (4) =
j'(4) =
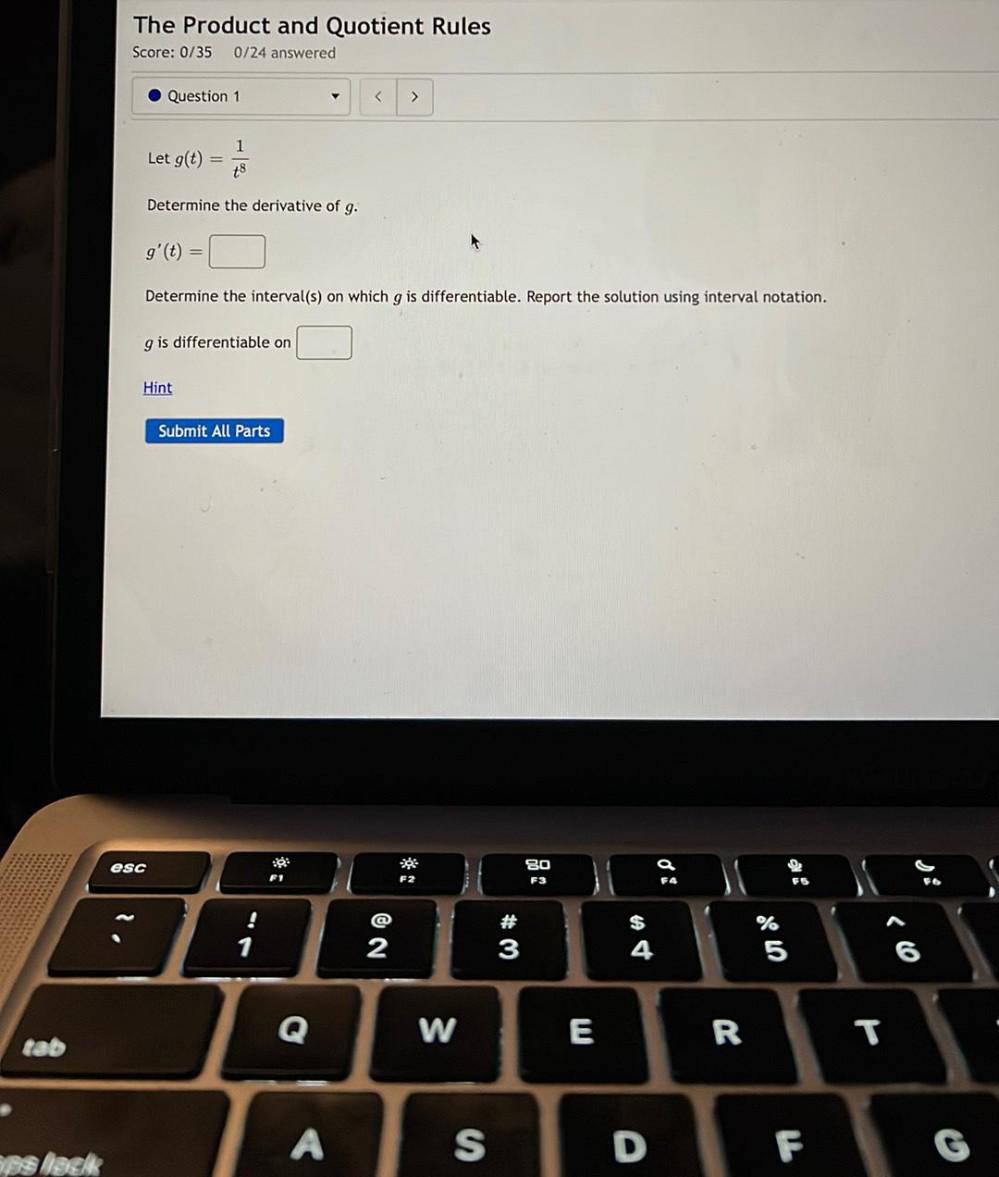
Calculus
DifferentiationLet g(t) = 1/t⁸
Determine the derivative of g.
g' (t) =
Determine the interval(s) on which g is differentiable. Report the solution using interval notation.
g is differentiable on
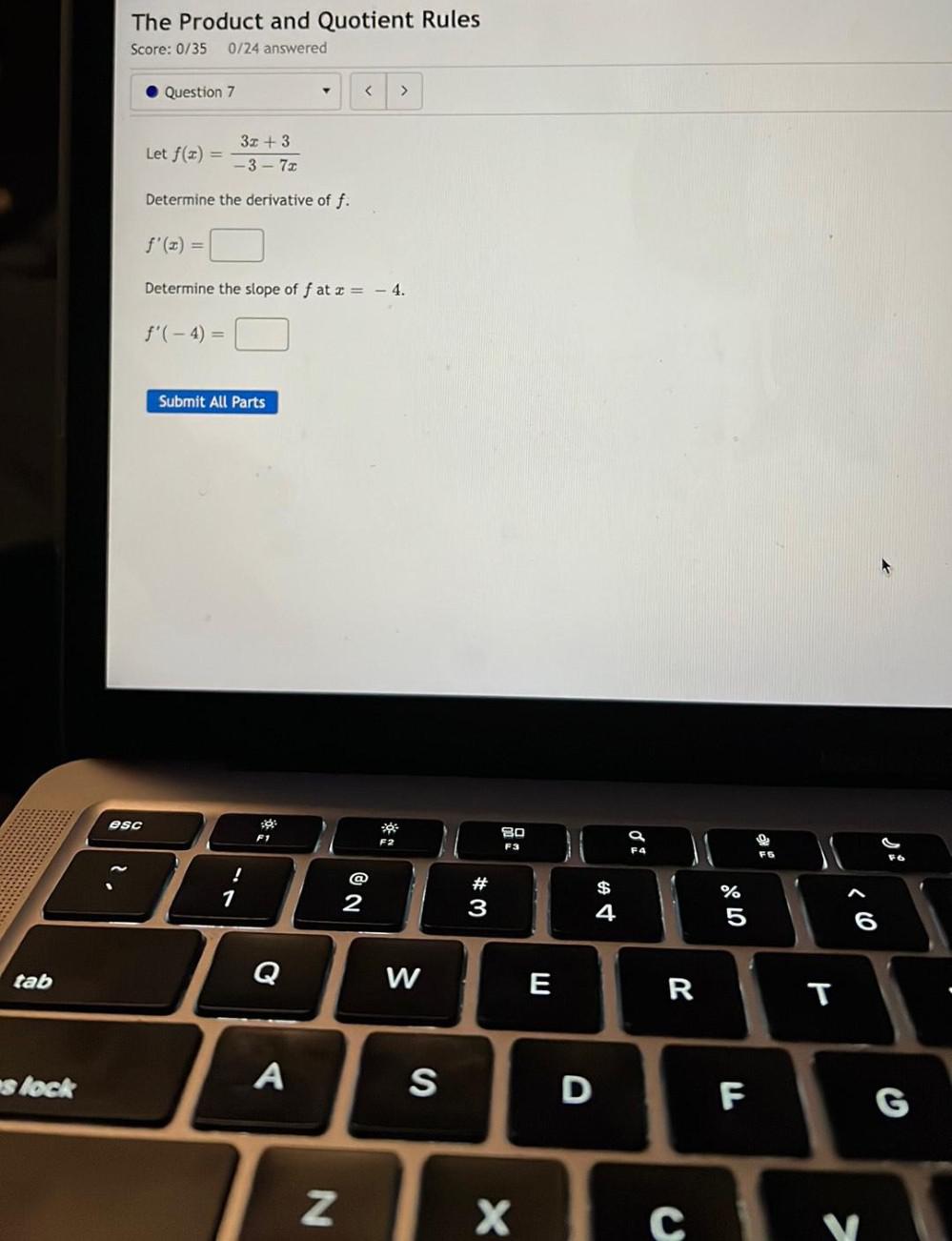
Calculus
DifferentiationLet f(x) = (3x + 3)/(-3-7x)
Determine the derivative of f.
f'(x) =
Determine the slope of f at x = - 4.
f'(-4)=