Indefinite Integration Questions and Answers

Calculus
Indefinite IntegrationEvaluate the integral by making the given substitution Jsec 4 4x tan 4x dx U 4x

Calculus
Indefinite IntegrationConsider the indefinite integral U This can be transformed into a basic integral by letting du 3 f and da x 7 dx Performing the substitution yields the integral

Calculus
Indefinite IntegrationEvaluate the integral 5 32 fa 26 11 de by making the substitution u x x6 C 11 NOTE Your answer should be in terms of r and not u
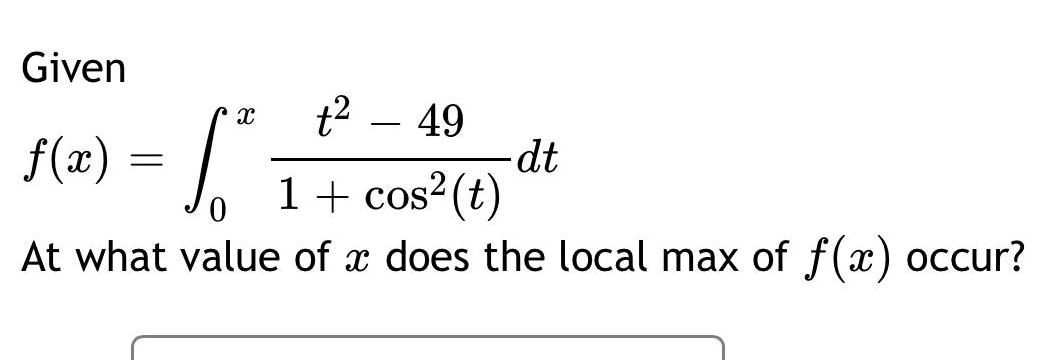
Calculus
Indefinite IntegrationGiven X f x So 0 At what value of a does the local max of f x occur t 49 1 cos t dt

Calculus
Indefinite IntegrationFor the following function f find the antiderivative F that satisfies the given condition f t sec t F 0 1 F t

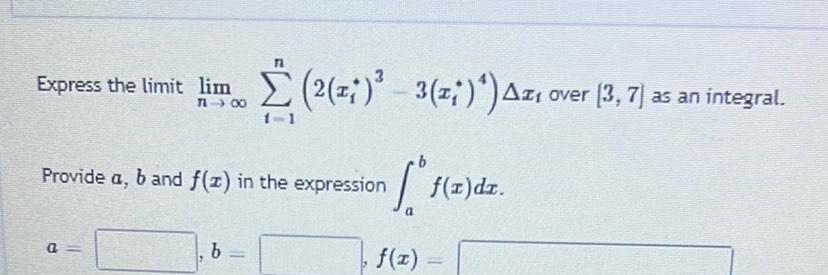
Calculus
Indefinite IntegrationExpress the limit lim 7 80 Provide a b and f z in the expression a 2 z 3 z Az over 3 7 as an integral 7 1 1 b a f x dr f x
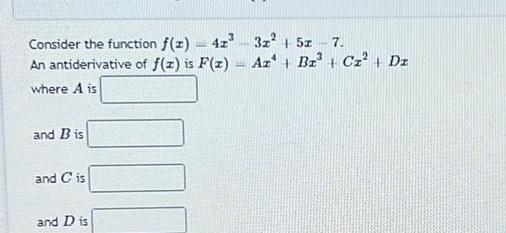
Calculus
Indefinite IntegrationConsider the function f x 42 3x 5x 7 An antiderivative of f z is F z Az Bz C Dz where A is and 13 is and C is and Dis
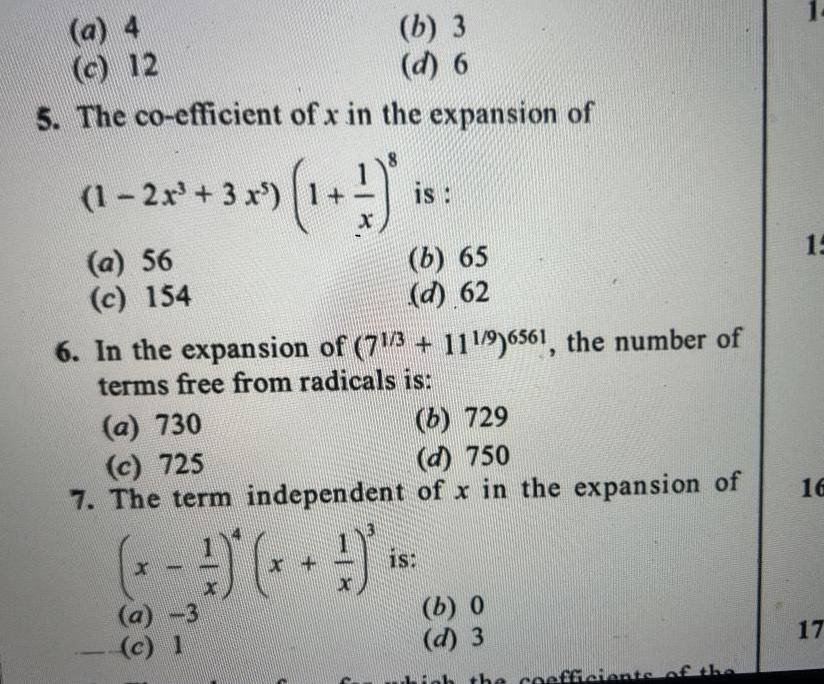
Calculus
Indefinite Integrationa 4 c 12 5 The co efficient of x in the expansion of 1 2x 3 x 1 a 56 c 154 b 3 d 6 x 1 3 is 6 In the expansion of 71 3 111 9 6561 the number of terms free from radicals is 63 b 65 d 62 a 730 b 729 c 725 d 750 7 The term independent of x in the expansion of 18 b 0 d 3 he coefficients of the 1 15 16 17

Calculus
Indefinite IntegrationNext question Let f z 82 z f z 20 z Get a similar question You 8 2 z Eden

Calculus
Indefinite IntegrationA B Integrating both sides indefinitely and using the fact that the integral of a sum is the sum of the integrals we find that D E d sin x de zcos 2 dez sin x dr In this last equation evaluate the indefinite integral on the left side as well as the rightmost indefinite integral on the right Upload picture here ii In the most recent equation from i solve the equation for the expression x cos x dx Upload picture here iii For which product of basic functions have you now found th F

Calculus
Indefinite Integration2 3 4 5 6 7 8 19 20 21 A E b For each of the following functions use your work in a to help you determine the general antiderivative of the function Recall that the general antiderivative of a function includes C to reflect the entire family of functions that share the same derivative Label each antiderivative by name e g the antiderivative of m should be called M In addition check your work by computing the derivative of each proposed antidarivative B i m x e x ii n x cos 5x 1 D iv v x 2 7x v w x 34 11x c Based on your experience in parts a and b conjecture an antiderivative for each of the following functions Test your conjectures by computing the derivative of each proposed antiderivative i a x cos x ii b x 4x 7 F

Calculus
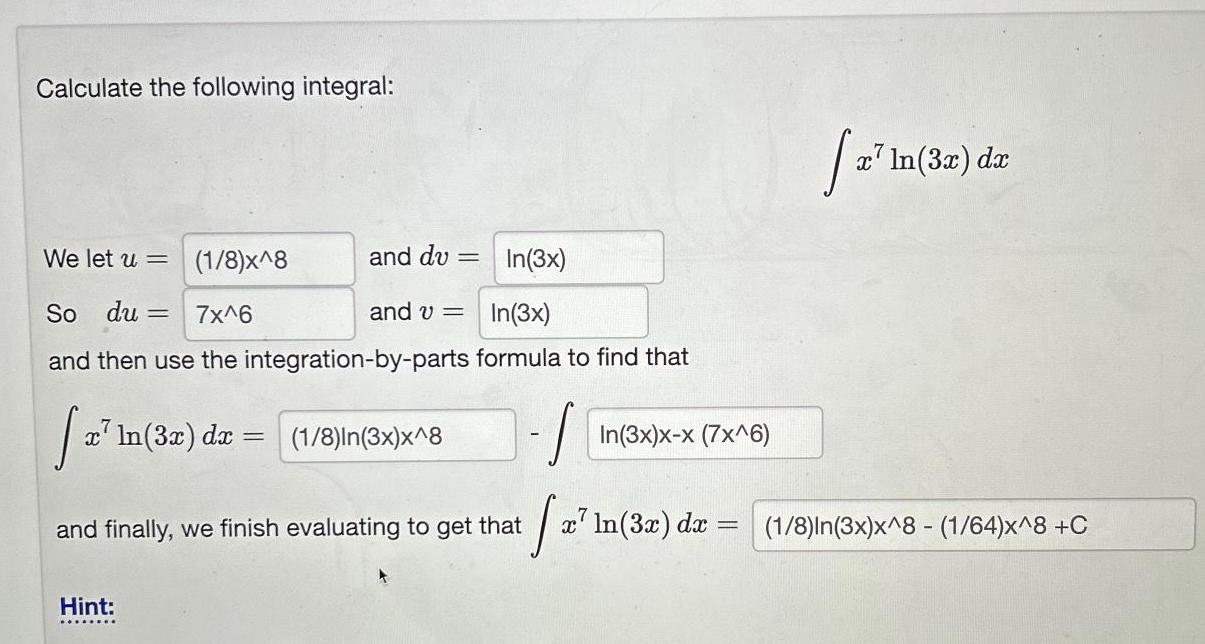
Indefinite IntegrationCalculate the following integral We let u So du 1 8 x 8 7x 6 In 3x and then use the integration by parts formula to find that 2 In 32 dr 1 8 In 3x x 8 S and du Hint In 3x and v and finally we finish evaluating to get that x In 3x x x 7x 6 x In 3x dx a In x In 3x dx 1 8 In 3x x 8 1 64 x 8 C

Calculus
Indefinite IntegrationFind a polynomial f x of degree 4 that has the following zeros 9 1 4 0 Leave your answer in factored form f x 0 4

Calculus
Indefinite Integration14 If sin A sin B 3 and angles A and B are acute angles what is the value of cos A B 13 a 12 b d 33 63

Calculus
Indefinite IntegrationMatch the following items On the unit circle with its center at 0 0 an arc with central point P 1 0 and terminal point T h length x

Calculus
Indefinite IntegrationWhen solving using the method of separation of variables the 1D wave equation 0 x t 0 u z 0 0 u 0 t 0 u x t 0 we assume the solution to the Partial Differential Equation and after substitution we get the two Ordinary Differential Equations O D E s A O D E in space where A is the separation constant The C UE subject to u a 0 2 x 2 P D E as u x t A O D E in time and solution to the problem is therefore u z t A cos A Cos B sint 1 1 and B where A Hint Use pi fort and for the fractional use abc d

Calculus
Indefinite IntegrationLet f 0 R be a bounded function Consider the functions g h 0 00 h x inf f y y r for every x 0 a 10 points Explain why g h are well defined R that are defined by g x sup f y y a and b 20 points Prove that lim f x 818 lim g x and lim h r exists and HIX 818 exists if and only if the limits lim g x lim h r 348 818

Calculus
Indefinite Integration3 16 points Find the volume of revolution resulting from the region bounded by x y 2 and y x being revolved around the x axis Use the shell 3x y 2 0 method
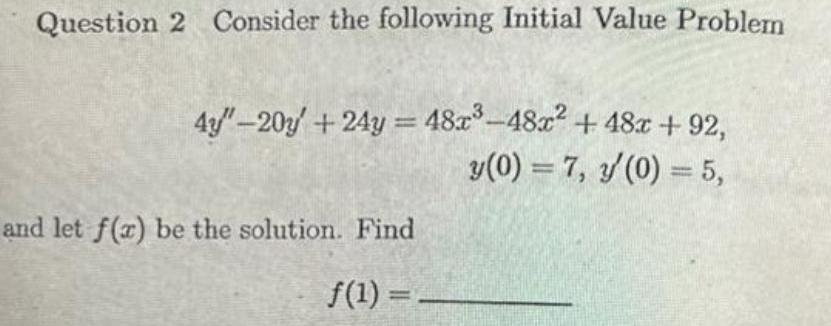
Calculus
Indefinite IntegrationQuestion 2 Consider the following Initial Value Problem 4y 20y 24y 48x 48x 48x 92 y 0 7 3 0 5 and let f x be the solution Find f 1

Calculus
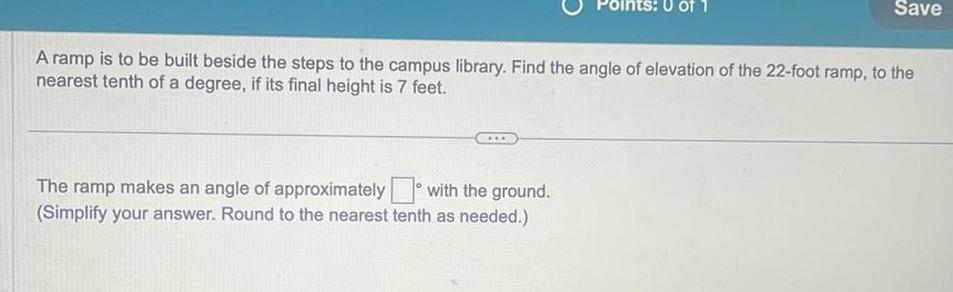
Indefinite IntegrationPoints 0 of 1 A ramp is to be built beside the steps to the campus library Find the angle of elevation of the 22 foot ramp to the nearest tenth of a degree if its final height is 7 feet The ramp makes an angle of approximately with the ground Simplify your answer Round to the nearest tenth as needed Save
Calculus
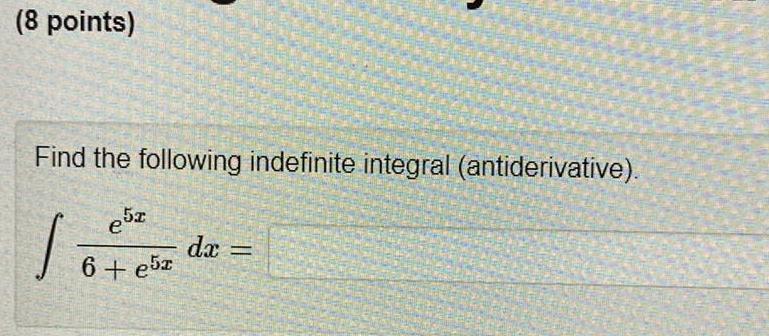
Indefinite Integration8 points Find the following indefinite integral antiderivative esa 1 6 e5r dx

Calculus
Indefinite Integrationind the most general antiderivative of the function Check your answer by differentiation Use C for the constant of the antiderivative f a 5 2e0 4q
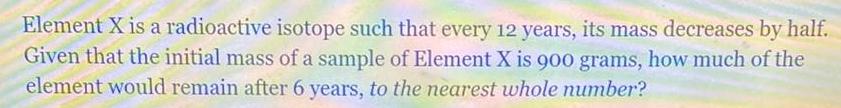
Calculus
Indefinite IntegrationElement X is a radioactive isotope such that every 12 years its mass decreases by half Given that the initial mass of a sample of Element X is 900 grams how much of the element would remain after 6 years to the nearest whole number
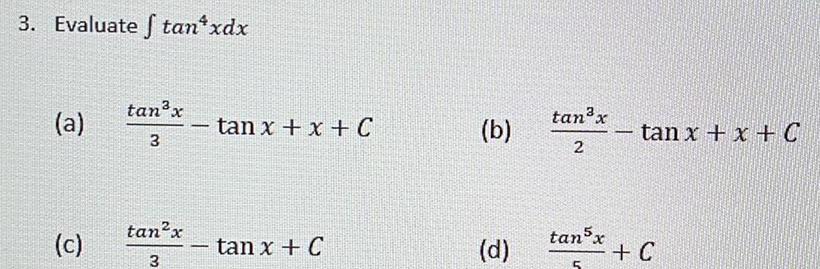
Calculus
Indefinite Integration3 Evaluate tan xdx a c tan x 3 tan x 3 tan x x C tan x C b d tan x 2 tan5x 5 tan x x C C

Calculus
Indefinite Integration10 Find the area of the region enclose by the curves y x 2 y x x 0 and x 1 31 a 3 32 c H 3 b d 5 65 3
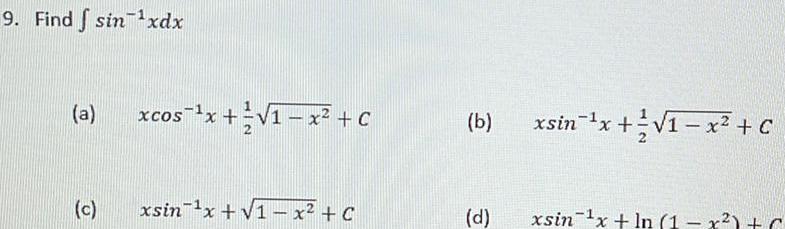
Calculus
Indefinite Integration9 Find sinxdx a c xcos x 1 x C xsin x 1 x C b d xsin x 1 x C 1x 1 xsin x ln 1 x C
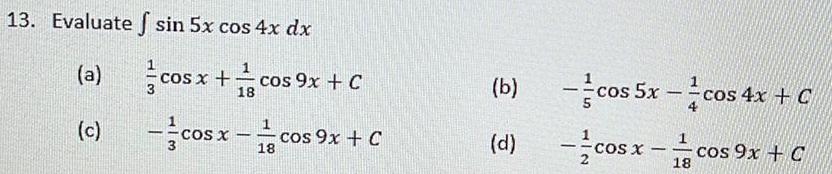
Calculus
Indefinite Integration13 Evaluate sin 5x cos 4x dx a c co cos x cos 9x C 18 cosx co 18 cos 9x C b d cos 5x c cos 4x C cosx to 1 18 cos 9x C
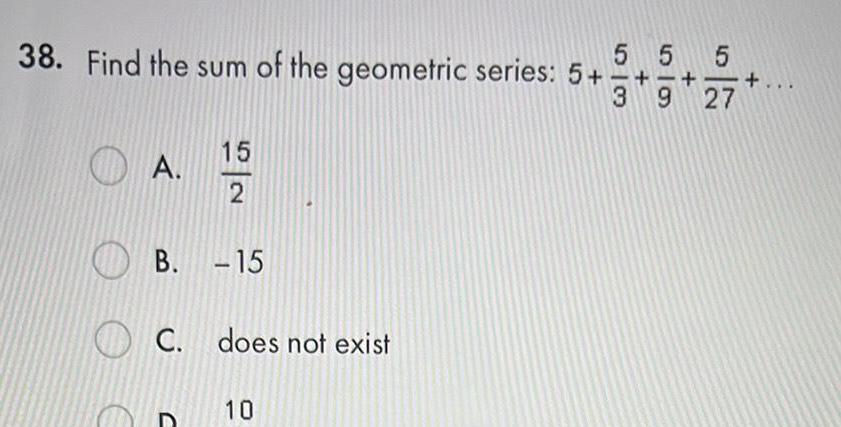
Calculus
Indefinite Integration5 38 Find the sum of the geometric series 5 3 A 15 2 B 15 C does not exist 10 5 5 9 27

Calculus
Indefinite Integrationind the indefinite integral Remember to use absolute values where appropriate Use C for the constant of integra sec x tan x sec x 3 dx

Calculus
Indefinite IntegrationWhich is an antiderivative of tan²xcscx?
secx-1
-cscx
tanx+5
No antiderivative exists

Calculus
Indefinite IntegrationLet f(x) = 1 + x2 for x E (-0,00) and let g(x)=tan(a) for x E (-1/2, T/2). Which of
the following statement is truc?
for a E (-1/2, 1/2).
d
(b)(f(x) + g(x)) = 2x + scc(e) for x € (-7/2, 7/2).
(a)
e
2x tan(x)
d g(x)
da f(x)(1+x2)2
=
d
(c) (f(r)g(x)) = scc²(x)(1+z²) + 2x tan(x) for x = (-1/2, 1/2).
dr
d
(d)
f(g(x)) = 2g(x) for r € (-1/2, 1/2).
dr
(e) None of the above statements is truc.


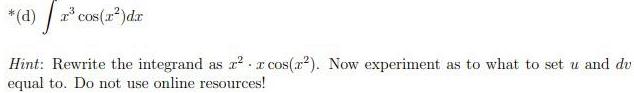
Calculus
Indefinite Integration*(d)
r³ cos(x²)dr
Hint: Rewrite the integrand as r²r cos(x²). Now experiment as to what to set u and du
equal to. Do not use online resources!

Calculus
Indefinite IntegrationUse Newton's method to find the absolute maximum value of the function f(x) = 2x sin(x), 0 ≤ x ≤ correct to six decimal places.
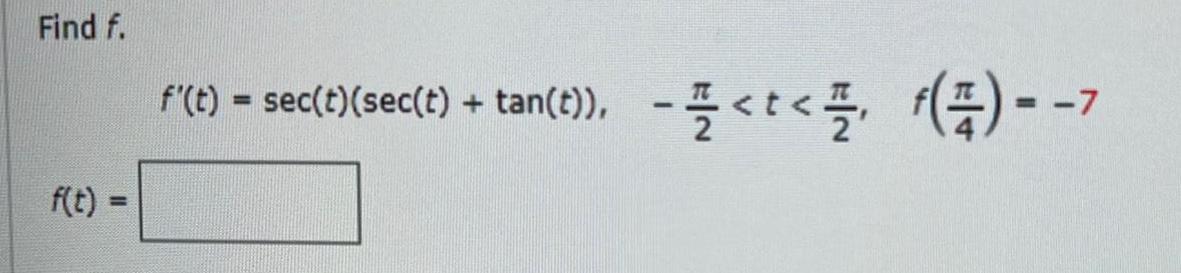
Calculus
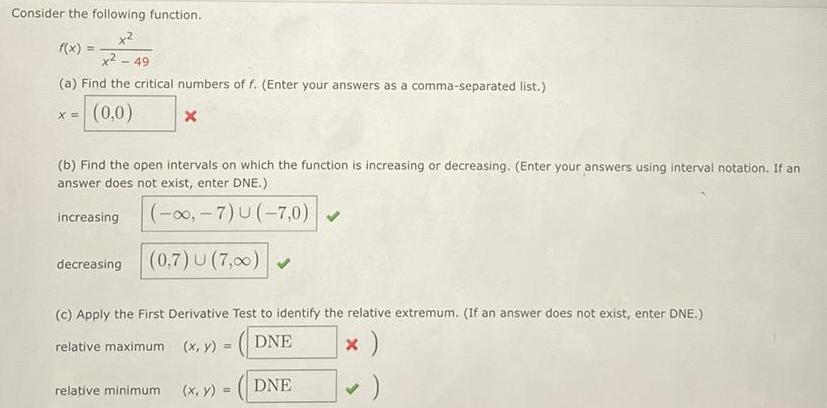
Indefinite IntegrationConsider the following function.
x²
f(x) =
x²-49
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
(0,0)
x
X =
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation. If an
answer does not exist, enter DNE.)
(-∞, -7)U(-7,0)
(0,7) U (7,0)
increasing
decreasing
(c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)
relative maximum
(x, y) =
DNE
x )
relative minimum
(x, y) =
DNE
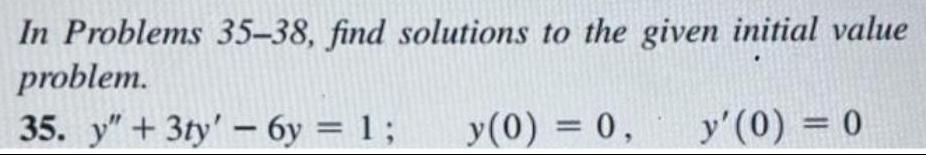
Calculus
Indefinite IntegrationIn Problems 35-38, find solutions to the given initial value
problem.
35. y" + 3ty' - 6y = 1;
y(0) = 0, y'(0) = 0
![Explain why Rolle's Theorem does not apply to the function even though there exist a and b such that f(a) = f(b). (Select all that apply.)
f(x) =
[л, 3x]
= cot
,
f(a) does not equal f(b) for all possible values of a and b in the interval [, 3x].
There are points on the interval (a, b) where f is not differentiable.
None of these.
There are points on the interval [a, b] where f is not continuous.
f '(a) does not equal f '(b) for any values in the interval [x, 3x].
X](https://media.kunduz.com/media/sug-question/raw/84126048-1660406061.7578588.jpeg?w=256)
Calculus
Indefinite IntegrationExplain why Rolle's Theorem does not apply to the function even though there exist a and b such that f(a) = f(b). (Select all that apply.)
f(x) =
[л, 3x]
= cot
,
f(a) does not equal f(b) for all possible values of a and b in the interval [, 3x].
There are points on the interval (a, b) where f is not differentiable.
None of these.
There are points on the interval [a, b] where f is not continuous.
f '(a) does not equal f '(b) for any values in the interval [x, 3x].
X

Calculus
Indefinite IntegrationFind the Fourier series of sin²x and cos²x without directly calculating the Fourier coefficients. (Use some standard trigonometric identities)
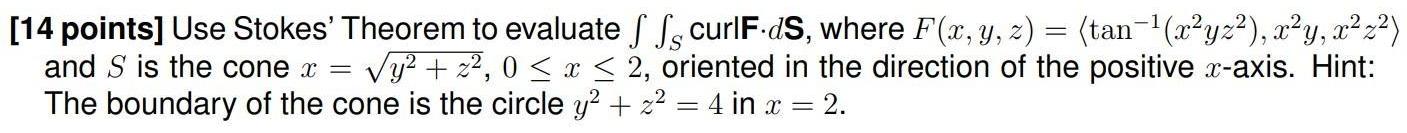
Calculus
Indefinite IntegrationUse Stokes' Theorem to evaluate ∫ ∫S curlF.ds, where F(x, y, z) = (tan-¹(x²yz²), x²y, x² z²) and S is the cone x = √y² + z²,0 ≤ x ≤ 2, oriented in the direction of the positive x-axis. Hint: The boundary of the cone is the circle y² + z² = 4 in x = 2.
![11:41
"He should do his homework
a little better, because he'll
find out that we've had a 10
decline of 5 million in the farm
population under these
government programs. He'll
also find that the Democratic
administration has sought to
get from Congress [an]
extension of the farm
program to include that
three-fourths that is now
free."
A. Reagan bases his argument on fact - "He
should do his homework a little better."
B. Reagan bases his argument on fact --
"we've had a decline of 5 million in the farm
population."
C. Reagan's argument is speculation -
"we've had a decline of 5 million in the farm
population."
D. Reagan bases his argument on emotion
-- "we've had a decline of 5 million in the
farm population."](https://media.kunduz.com/media/sug-question/raw/84061445-1660326383.0930817.jpeg?w=256)
Calculus
Indefinite Integration11:41
"He should do his homework
a little better, because he'll
find out that we've had a 10
decline of 5 million in the farm
population under these
government programs. He'll
also find that the Democratic
administration has sought to
get from Congress [an]
extension of the farm
program to include that
three-fourths that is now
free."
A. Reagan bases his argument on fact - "He
should do his homework a little better."
B. Reagan bases his argument on fact --
"we've had a decline of 5 million in the farm
population."
C. Reagan's argument is speculation -
"we've had a decline of 5 million in the farm
population."
D. Reagan bases his argument on emotion
-- "we've had a decline of 5 million in the
farm population."
