Limits & Continuity Questions and Answers
Calculus
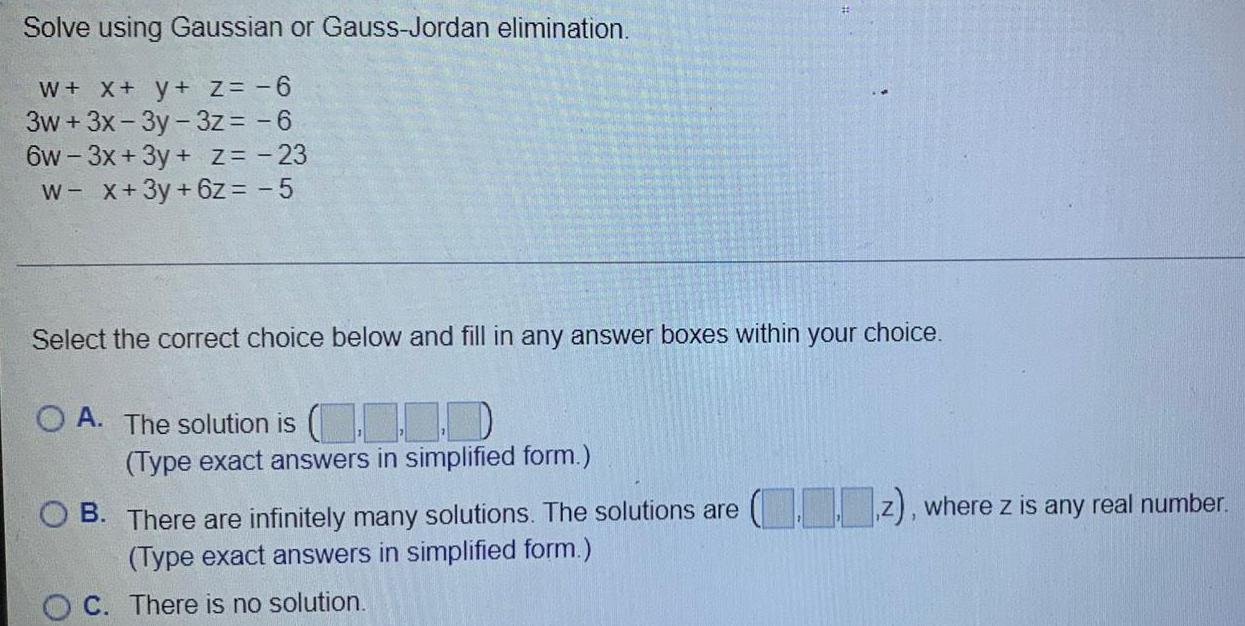
Limits & ContinuitySolve using Gaussian or Gauss-Jordan elimination.
w + x + y + z = -6
3w+ 3x-3y-3z=-6
6w-3x+3y + z = -23
w- x + 3y + 6z = -5
Select the correct choice below and fill in any answer boxes within your choice.
A. The solution is (
(Type exact answers in simplified form.)
B. There are infinitely many solutions. The solutions are (z), where z is any real number.
(Type exact answers in simplified form.)
C. There is no solution.
Calculus
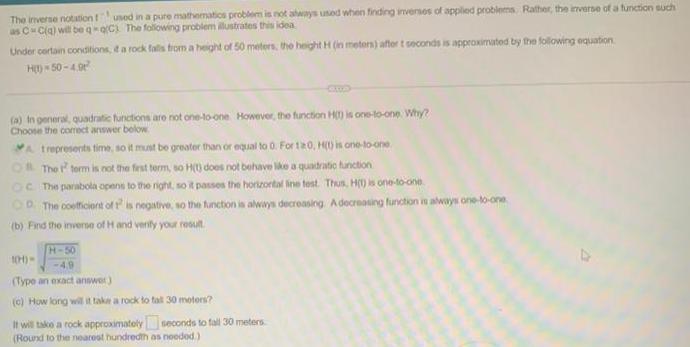
Limits & ContinuityThe inverse notation f-1 used in a pure mathematics problem is not always used when finding inverses of applied problems. Rather, the inverse of a function such as C=C(q) will be q=qC). The following problem illustrates this idea.
Under certain conditions, e a rock falls from a height of 50 meters, the height H (in meters) after t seconds is approximated by the following equation
H(t)=50-4.9t²
(a) in general, quadratic functions are not one-to-one. However, the function H(t) is one-to-one. Why?
Choose the correct answer below
A. t represents time, so it must be greater than or equal to 0. For t≥0, H(t) is one-to-one
B The t2 term is not the first term, so H(t) does not behave like a quadratic function
C The parabola opens to the right, so it passes the horizontal line test. Thus, H(t) is one-to-one
D The coefficient of t2 is negative, so the function is always decreasing. A decreasing function is always one-to-one
(b) Find the inverse of H and verify your result
(Type an exact answer)
(c) How long will it take a rock to fall 30 moters?
It will take a rock approximately seconds to fall 30 meters
(Round to the nearest hundredth as needed)
![Find A-1, or explain why it does not exist.
A[3 2]
2 1
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. A-¹=
B. A-1 does not exist because A in the augmented matrix [All] cannot be transformed to I using the Gauss-Jordan method.](https://media.kunduz.com/media/sug-question/raw/84570726-1658439824.5284905.jpeg?w=256)
Calculus
Limits & ContinuityFind A-1, or explain why it does not exist.
A[3 2]
2 1
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. A-¹=
B. A-1 does not exist because A in the augmented matrix [All] cannot be transformed to I using the Gauss-Jordan method.

Calculus
Limits & ContinuityGive the sums of the following geometric series (or state that series is divergent).
Leave your answers unsimplified.
(a) 4 9 + 28 45 + 196 225 +...+ 4.7121 9.5121
(b) 31 + 31 e + 31 e2 + 31 e3 +...
Calculus
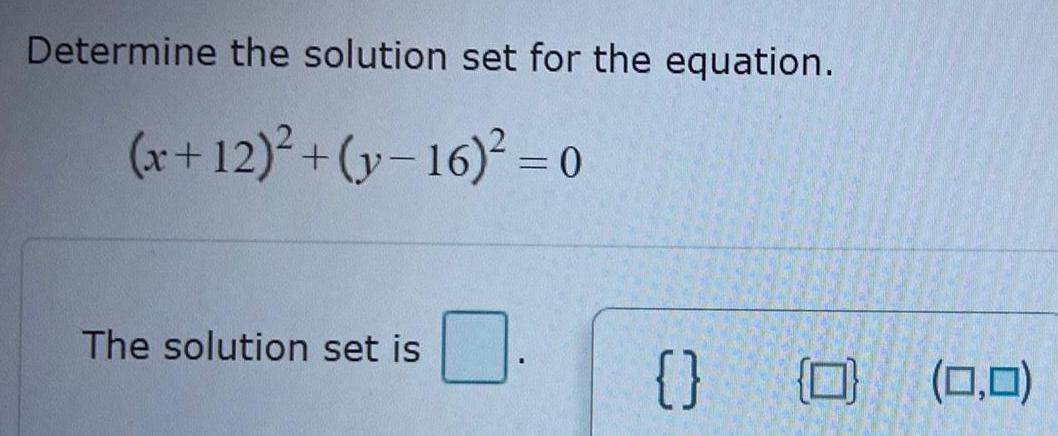
Limits & ContinuityDetermine the solution set for the equation.
(x+12)²+(y-16)² = 0
The solution set is
Calculus
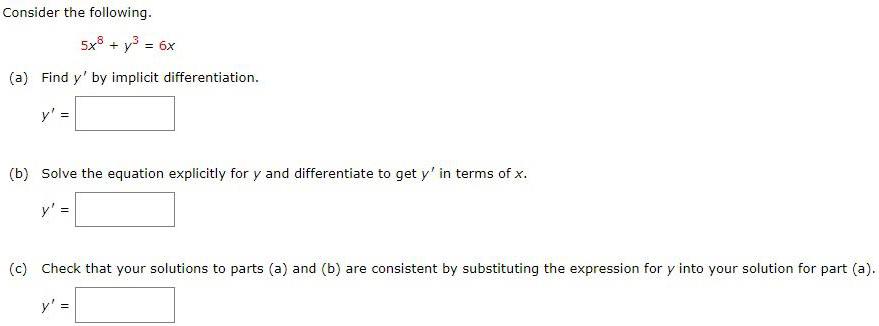
Limits & ContinuityConsider the following.
5x8 + y³ = 6x
(a) Find y' by implicit differentiation.
y' =
(b) Solve the equation explicitly for y and differentiate to get y' in terms of x.
y' =
(c) Check that your solutions to parts (a) and (b) are consistent by substituting the expression for y into your solution for part (a).
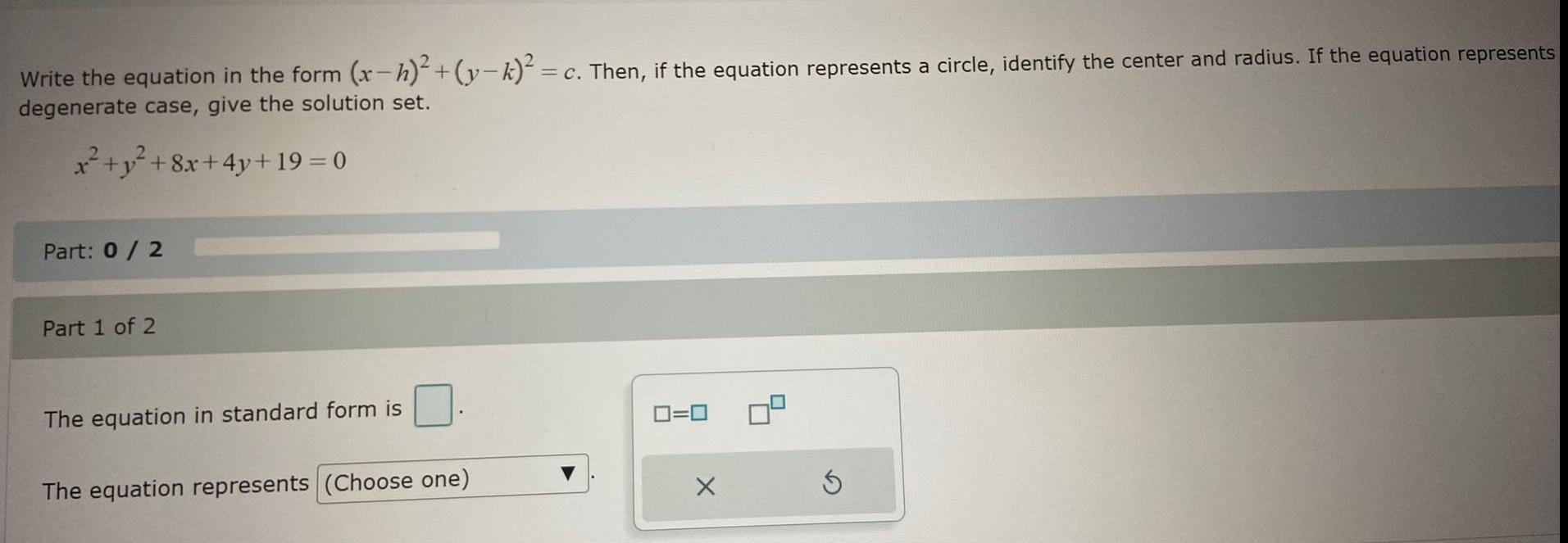
Calculus
Limits & ContinuityWrite the equation in the form (x-h)²+(y-k)² = c. Then, if the equation represents a circle, identify the center and radius. If the equation represents degenerate case, give the solution set.
x² + y² +8x+4y+ 19 = 0
Part: 0 / 2
Part 1 of 2
The equation in standard form is
The equation represents
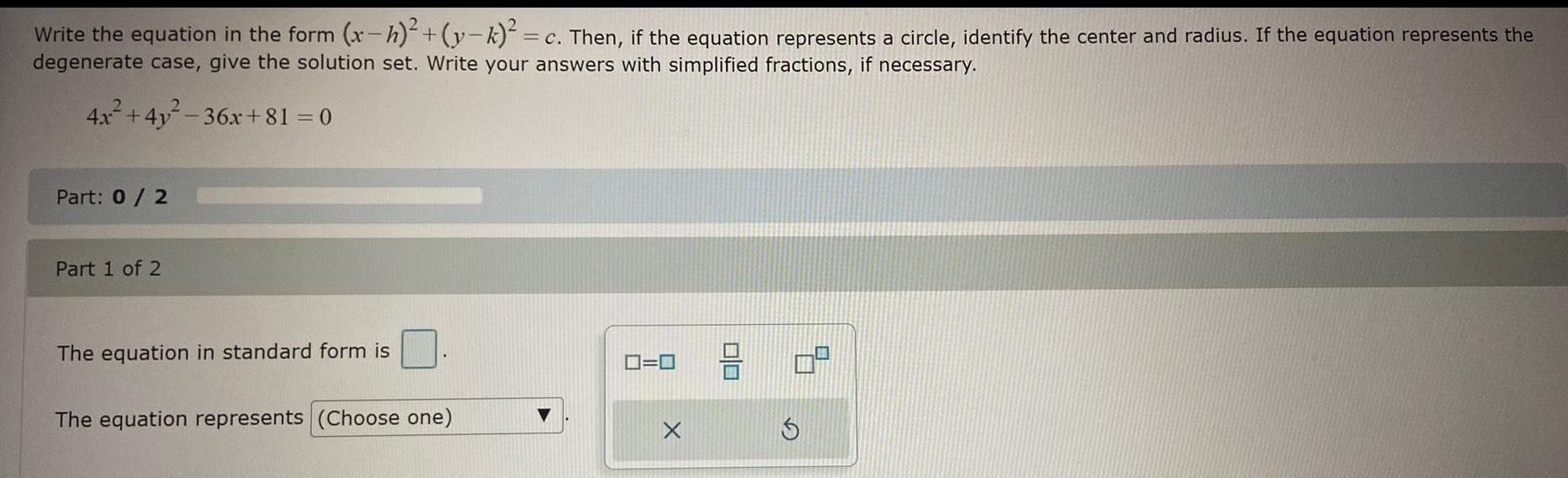
Calculus
Limits & ContinuityWrite the equation in the form (x-h)²+(y-k)² =c. Then, if the equation represents a circle, identify the center and radius. If the equation represents the degenerate case, give the solution set. Write your answers with simplified fractions, if necessary.
4x²+4y²-36x+81 = 0
Part: 0 / 2
Part 1 of 2
The equation in standard form is
The equation represents
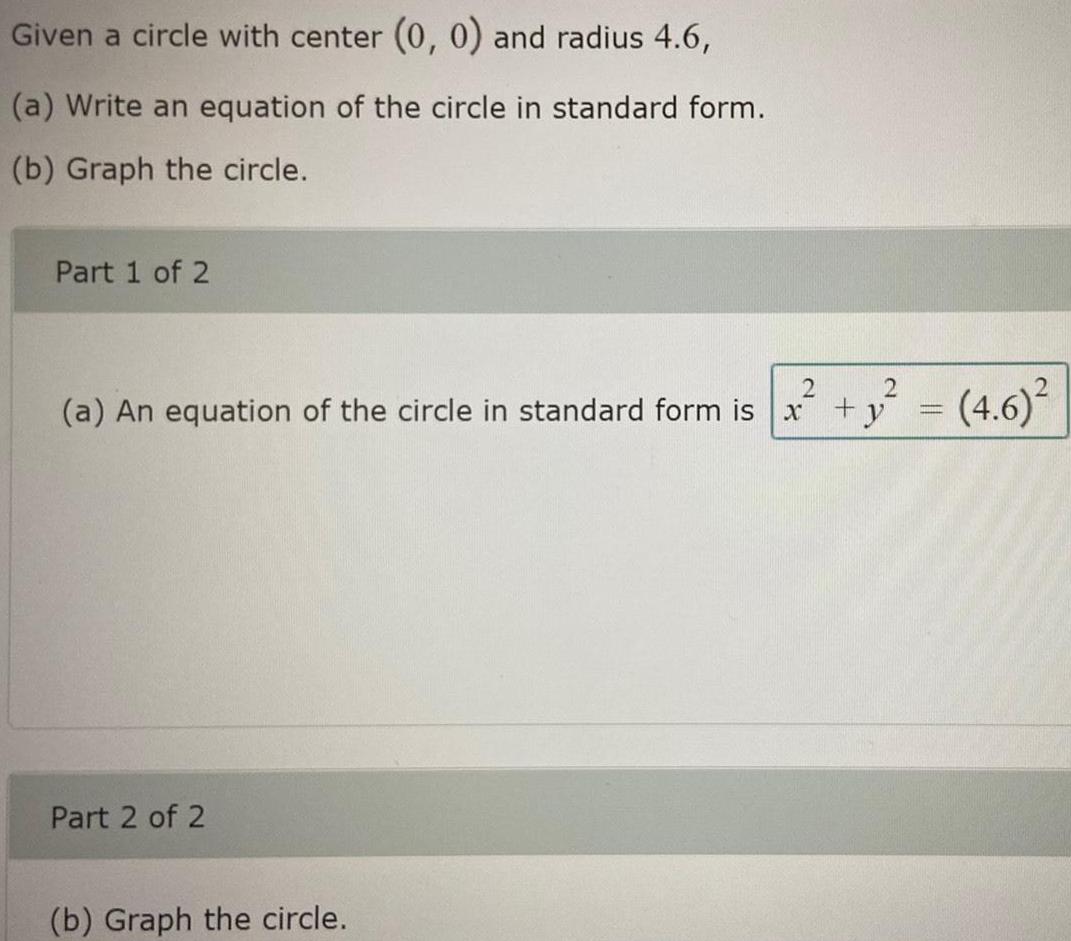
Calculus
Limits & ContinuityGiven a circle with center (0, 0) and radius 4.6,
(a) Write an equation of the circle in standard form.
(b) Graph the circle.
Part 1 of 2
(a) An equation of the circle in standard form is
Part 2 of 2
(b) Graph the circle.

Calculus
Limits & ContinuityFind the decimal approximation, rounded to two decimal places, of the solution of the equation.
5x = 30
Type your numeric answer and submit
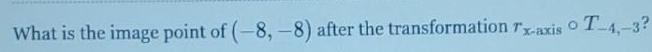
Calculus
Limits & ContinuityWhat is the image point of (-8,-8) after the transformation Tx-axis T-4,-3?

Calculus
Limits & ContinuityEvaluate the following using the change of base formula. Round the answer to 4 decimal places.
log7 63
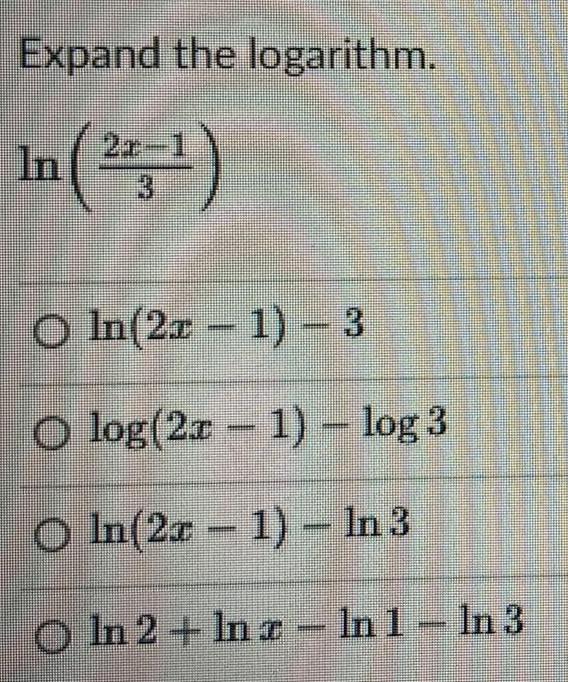
Calculus
Limits & ContinuityExpand the logarithm.
In (2x-1 3)
ln(2x - 1) - 3
log(2x - 1) - log 3
ln(2x - 1) - In 3
ln 2+ lnx - ln 1-ln 3

Calculus
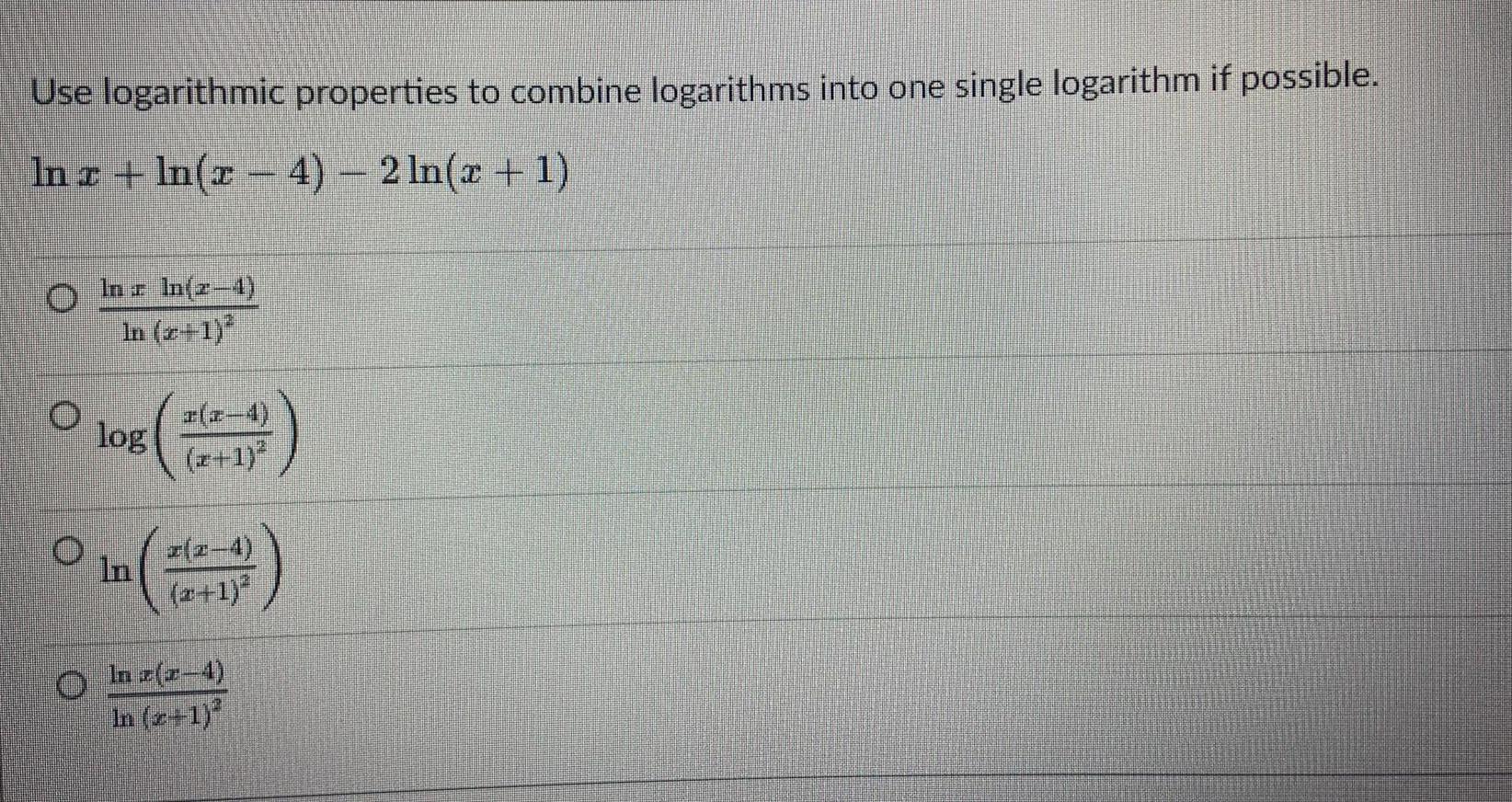
Limits & ContinuityUse logarithmic properties to combine logarithms into one single logarithm if possible.
Inx+ln(x-4) 2ln(x + 1)
In x ln(x-4)
In (x+1)²
log x(x-4)
(x+1)²
x(x-4)
(x+1)²
In x(x-4)
ln (x+1)²
Calculus
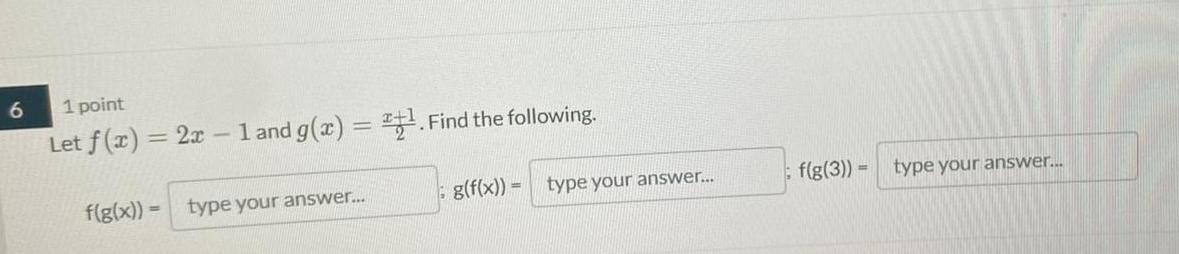
Limits & ContinuityLet f(x) = 2x - 1 and g(x) = x + 1 2. Find the following.
f(g(x)) =
g(f(x)) =
f(g(3)) =
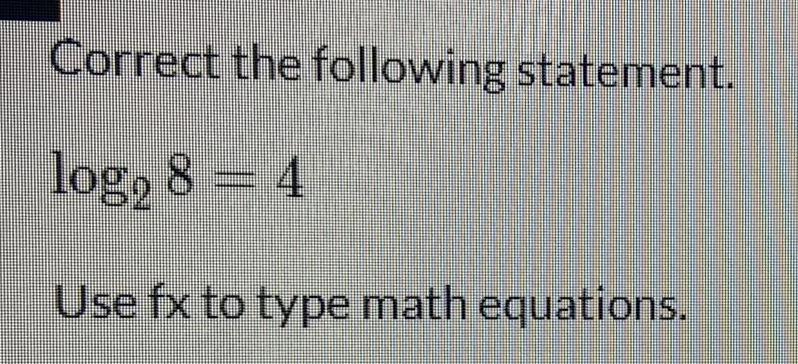
Calculus
Limits & ContinuityCorrect the following statement.
log2 8 = 4
Use fx to type math equations.

Calculus
Limits & ContinuityIdentify the base and exponent of the following exponential equation.
In A = x
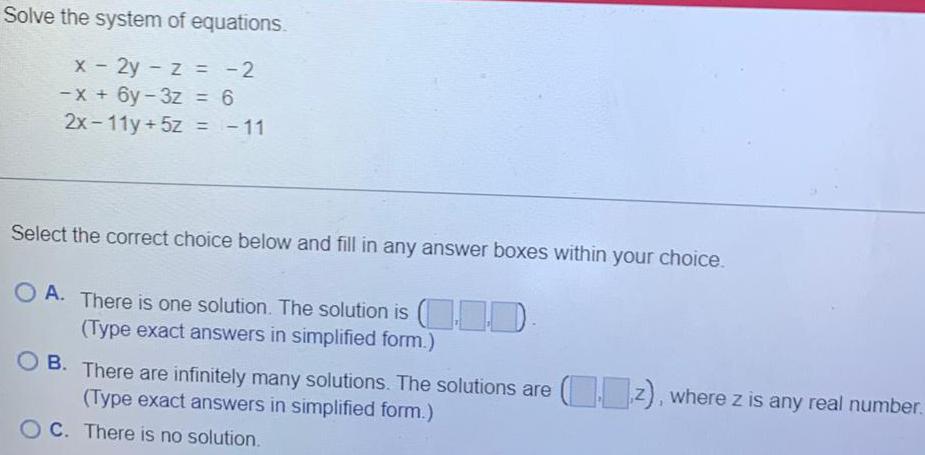
Calculus
Limits & ContinuitySolve the system of equations.
x - 2y - z = -2
-x + 6y - 3z = 6
2x - 11y + 5z = -11
Select the correct choice below and fill in any answer boxes within your choice.
A. There is one solution. The solution is 1.10.
(Type exact answers in simplified form.)
B. There are infinitely many solutions. The solutions are (z), where z is any real number.
(Type exact answers in simplified form.)
C. There is no solution.

Calculus
Limits & ContinuitySolve the system of equations.
2x-3y-5z = -4
6x-9y-15z = -3
2x-2y-3z=4
Select the correct choice below and fill in any answer boxes within your choice.
A. There is one solution. The solution is
(Type exact answers in simplified form.)
B. There are infinitely many solutions. The solutions are (z), where z is any real number.
(Type exact answers in simplified form.)
C. There is no solution.

Calculus
Limits & ContinuityDescribe the transformation of f(x) = sin x to g(x) = sin (x + π 3).
A. f(x) is shifted π 3 units up.
B. f(x) is shifted π 3 units down.
C. f(x) is shifted π 3 units to the left.
D. f(x) is shifted π 3 units to the right.


Calculus
Limits & ContinuitySketch a graph of the following functions. List the the domain and range of each function in interval notation.
(a) f(x) = 3x + 1
(b) g(x) = ln(x + 2)
(c) h(x) = log7(x) - 3
(d) f(x) = 2-x
(e) f(x) = log(-x)

Calculus
Limits & ContinuityUsing the unit circle, compute the exact value of sin (4π 3 + π 4)
-√2+√6
-√6-√2
none of these
√6+√2 4
√2-√6 4

Calculus
Limits & ContinuityLet f''(u) = e-4u
Find the particular solution to the above differential equation that satisfies the following initial conditions.
f'(0) = -9
• f(0) = 3

Calculus
Limits & ContinuityFrom a height of 69 meters, a softball is thrown vertically upward with a velocity of 17 meters per second. Determine the maximum height reached by the softball. Round the solution to the nearest hundredth, if necessary.

Calculus
Limits & ContinuityA nickle is tossed vertically from the roof of a building that is 46 meters tall. If the nickle impacts the ground after 3 seconds, determine the initial velocity, vo, of the nickle. Round the solution to the nearest hundredth, if necessary.

Calculus
Limits & ContinuitySuppose a person 6.6 feet tall throws a rock vertically upward. Determine the initial velocity, vo, of the rock, if the rock reaches a maximum height of 42.6 feet. Round the solution to the nearest integer.

Calculus
Limits & ContinuityUse the product of logarithms property to rewrite the expression. Simplify as much as possible. Enter the final result of the expression without any blank spaces.
log(100x)

Calculus
Limits & ContinuityUse log properties to rewrite the expression. Simplify as much as possible. Enter the final result without any spaces.
log 3²
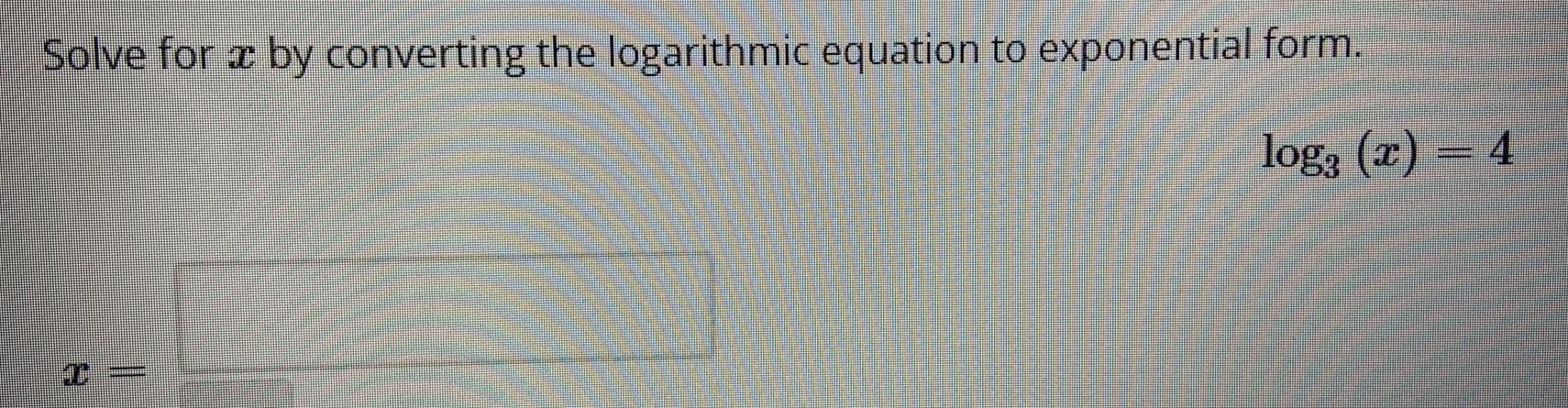
Calculus
Limits & ContinuitySolve for x by converting the logarithmic equation to exponential form.
logą (x) = 4

Calculus
Limits & ContinuityEvaluate the expression using a calculator. Round to the nearest thousandth.
In (√/0.76) =
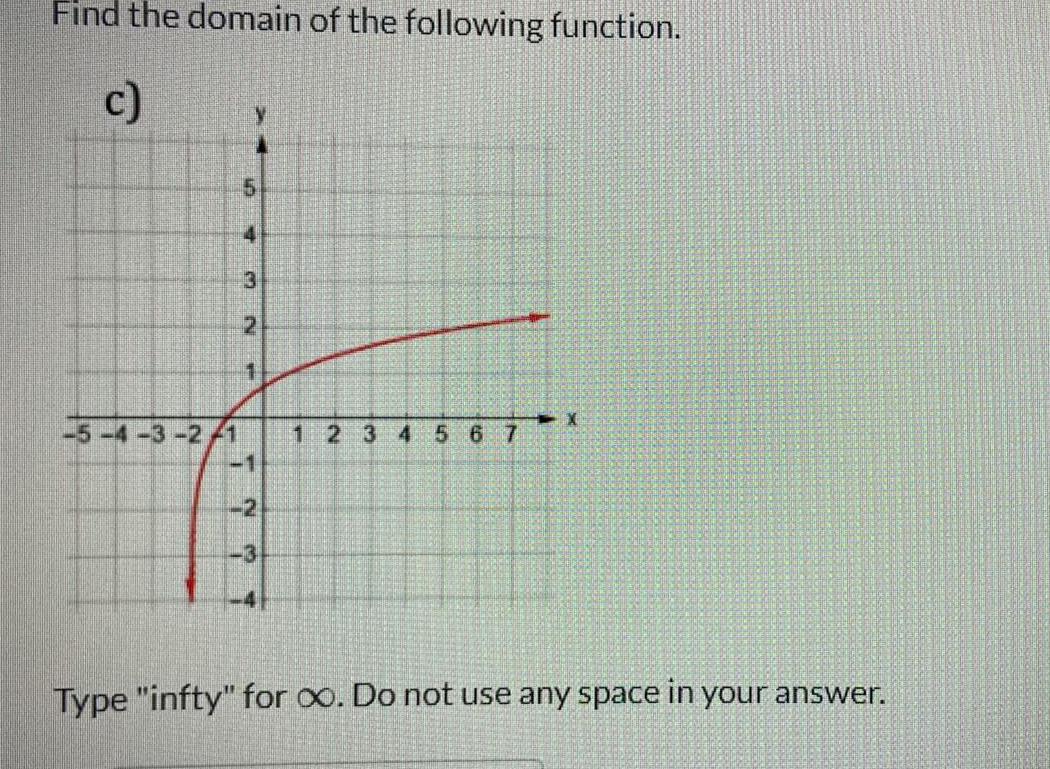
Calculus
Limits & ContinuityFind the domain of the following function.
Type "infty" for ∞. Do not use any space in your answer.

Calculus
Limits & ContinuityLet f(x) = 2log4(x - 1) + 3. Find the domain, range, and equation of the asymptote.
Domain: (1,∞)
Range: (-∞, ∞)
Equation of asymptote: y = 1
Domain: (1, ∞)
Range: (-∞, ∞)
Equation of asymptote: x = 3
Domain: (-∞, ∞)
Range: (1, 0)
Equation of asymptote: y = 1
Domain: (1, ∞)
Range: (-∞, ∞)
Equation of asymptote: y = 3
Domain: (-∞, ∞)
Range: (1, ∞)
Equation of asymptote: x=1
Domain: (1, ∞)
Range: (-∞,∞)
Equation of asymptote: x = 1

Calculus
Limits & ContinuityState the domain of the function. Give your answer as an inequality.
f(x) = ln (5-x)
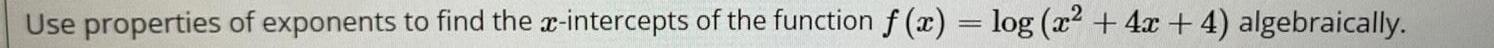
Calculus
Limits & ContinuityUse properties of exponents to find the x-intercepts of the function f(x) = log(x² + 4x + 4) algebraically.
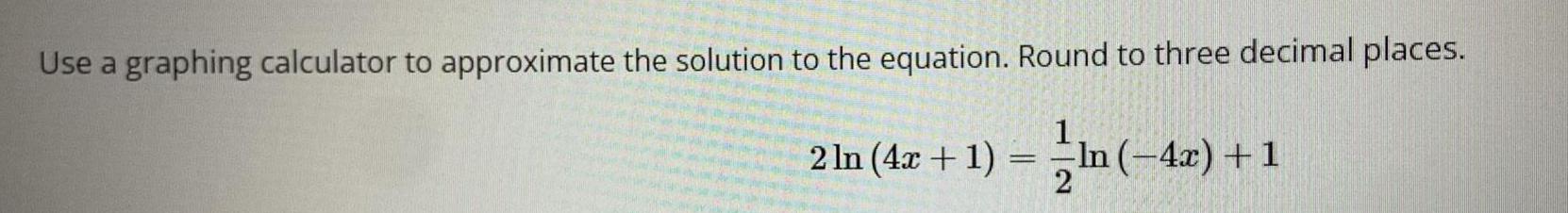
Calculus
Limits & ContinuityUse a graphing calculator to approximate the solution to the equation. Round to three decimal places.
2 ln (4x + 1) = 1 2In (-4x) + 1
Calculus
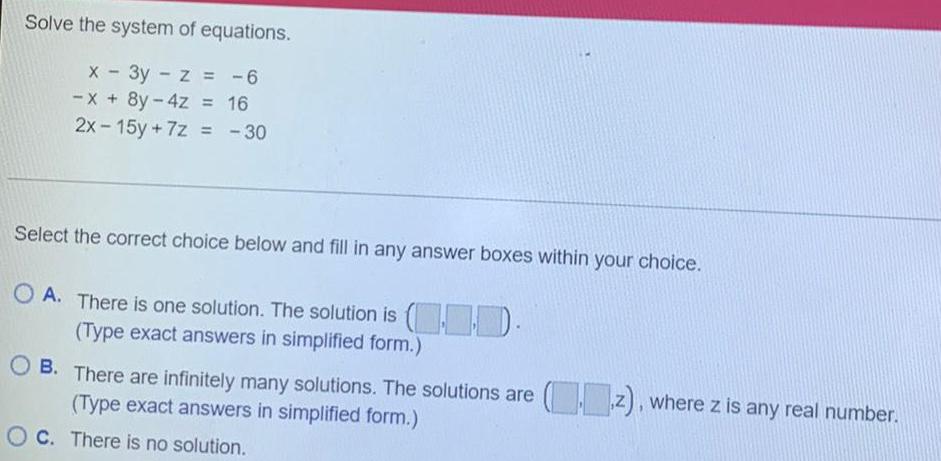
Limits & ContinuitySolve the system of equations.
x - 3y - z = -6
-x + 8y-4z = 16
2x-15y +7z = -30
Select the correct choice below and fill in any answer boxes within your choice.
A. There is one solution. The solution is
(Type exact answers in simplified form.)
B. There are infinitely many solutions. The solutions are (z), where z is any real number.
(Type exact answers in simplified form.)
C. There is no solution.
Calculus
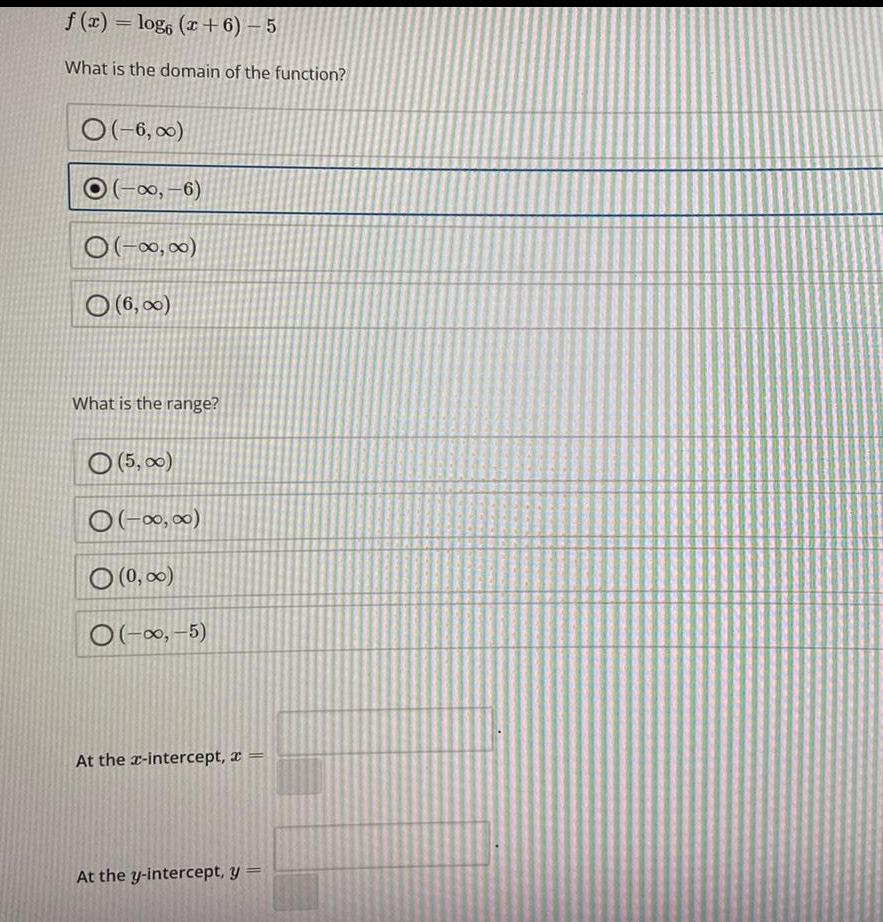
Limits & Continuityf(x) = log6 (x+6) − 5
What is the domain of the function?
(-6,∞)
(-∞, -6)
(-∞, ∞)
(6,∞)
What is the range?
(5,∞)
(-∞,∞)
(0,∞)
(-∞, -5)
At the x-intercept, x =
At the y-intercept, y =
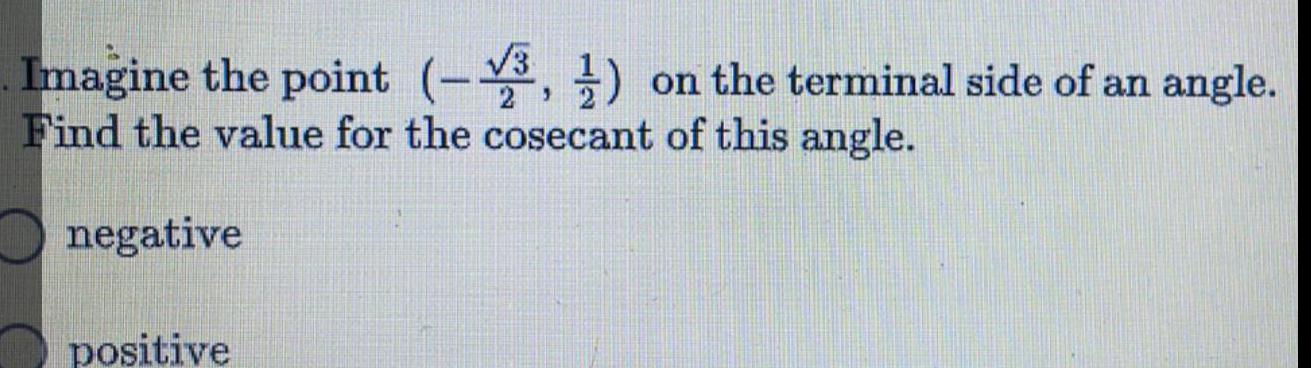
Calculus
Limits & ContinuityImagine the point (-√3 2, 1 2) on the terminal side of an angle.
Find the value for the cosecant of this angle.
negative
positive

Calculus
Limits & ContinuitySolve the following system of equations.
x + y + z = - 4
2x + 4y + 2z = - 18
-x + 7y - 3z = -34
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The solution is
(Type integers or simplified fractions.)
B. There are infinitely many solutions.
C. There is no solution.

Calculus
Limits & ContinuityIf the calculator gives us the following values for "a" and "b" in the form of y = ax + b, what should the regression equation (statistics form) look like? a=0.872, b = 25.263
(Note: In the choices below, assume that y is "y hat.")
y= 25.263+0.872x
y 25.263x + 0.872
y=0.872 +25.263x
y 0.872x+25.263

Calculus
Limits & ContinuitySuppose that a polynomial function of degree 4 with rational coefficients has -2+5i, 5-sqrt5 as zeros. Find the other zeros.
Calculus
Limits & ContinuityFor the function f(x)=x² +3, construct and simplify the difference quotient f(x+h)-f(x) h
The difference quotient is

Calculus
Limits & ContinuityA silver dollar is tossed vertically from the roof of a building that is 57 meters tall. If the silver dollar impacts the ground after 6 seconds, determine the initial velocity, vo, of the silver dollar. Round the solution to the nearest hundredth, if necessary.
v0 = meters per second
Was the silver dollar tossed off the building in an upward or downward fashion?
Downward
Upward

Calculus
Limits & ContinuityClick on the equivalent radical form of the exponential expression.
x7/2
7√x²
√x²
7√x
(√x2)7

Calculus
Limits & ContinuityA penny is tossed vertically from the roof of a building that is 126 feet tall. If the penny impacts the ground after 10 seconds, determine the initial velocity, v0, of the penny. Round the solution to the nearest hundredth, if necessary.
v0 = feet per second
Was the penny tossed off the building in an upward or downward fashion?
Upward
Downward

Calculus
Limits & ContinuityLet g''(v) = 36v
Find the particular solution to the above differential equation that satisfies the following initial conditions.
g'(0) = 6
g(5) = -2

Calculus
Limits & ContinuityLet d²h dz² = e7z
Find the particular solution to the above differential equation that satisfies the following initial conditions.
h'(0) = -3
h(0) = 1

Calculus
Limits & ContinuityA particular cookie recipe calls for 1 6 cups of butter to make 3 dozen cookies. Giselle needs to make 24 dozen cookies for the bake sale. How many cups of butter will she need?
Giselle needs cups of butter