Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Geometry
Coordinate systemAndrea earns 165 for each digital projector that she sells If she works 5 days a week for 11 hours each day and sells 12 digital projectors a week on average what is her average hourly wage OA 15 an hour OB 33 an hour OC 36 an hour O D 55 an hour

Geometry
Coordinate system25x 0 x 38 The equation y 30 x 38 950 x 38 represents Jordan s overtime pay structure Based on this equation after how many hours does Jordan start earning overtime pay A 950 B 25 O C 30 D 38
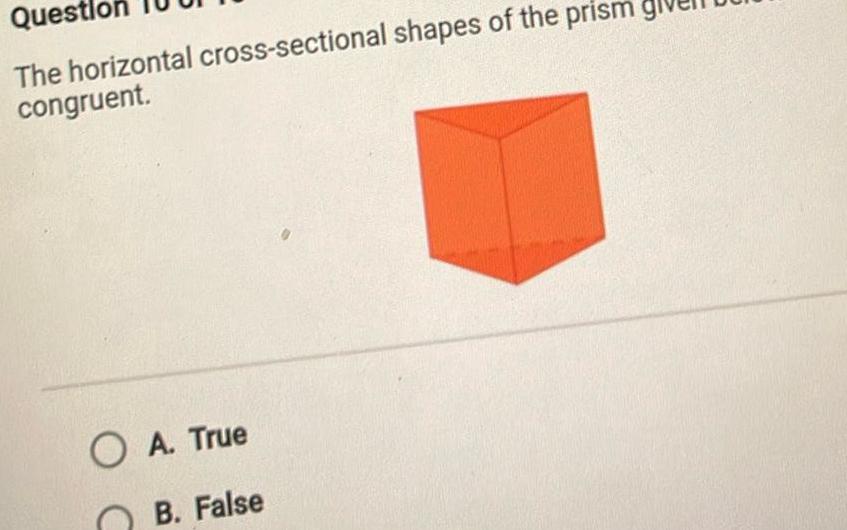
Geometry
2D GeometryA polygon is a solid bounded by the polygonal regions formed by intersecting planes OA True B False
Geometry
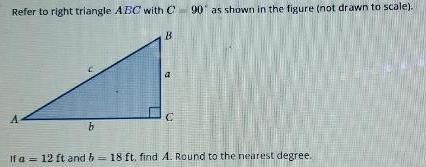
3D GeometryRefer to right triangle ABC with C 90 as shown in the figure not drawn to scale A b B C If a 12 ft and b 18 ft find A Round to the nearest degree
Geometry
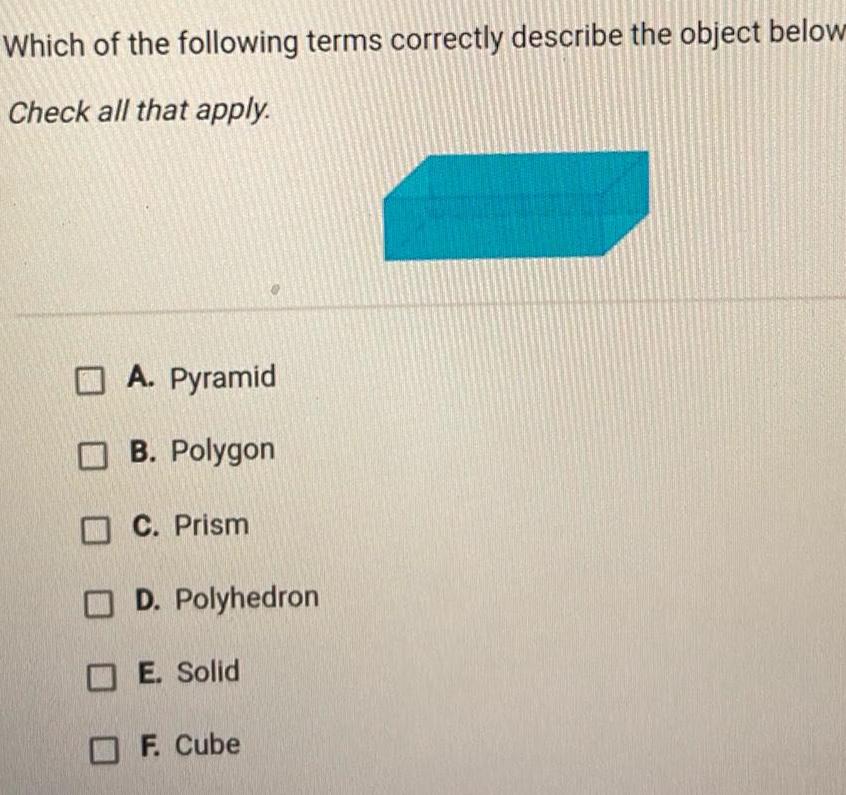
3D GeometryWhich of the following terms correctly describe the object below Check all that apply A Pyramid B Polygon C Prism D Polyhedron E Solid F Cube

Geometry
3D GeometryA pyramid has cross sectional shapes taken parallel to its base that are to one another O A equivalent OB congruent O C similar O D equal

Geometry
3D GeometryHow many faces does a pyramid with a square base have OA Five OB Eight O C Seven OD Six 0
Geometry
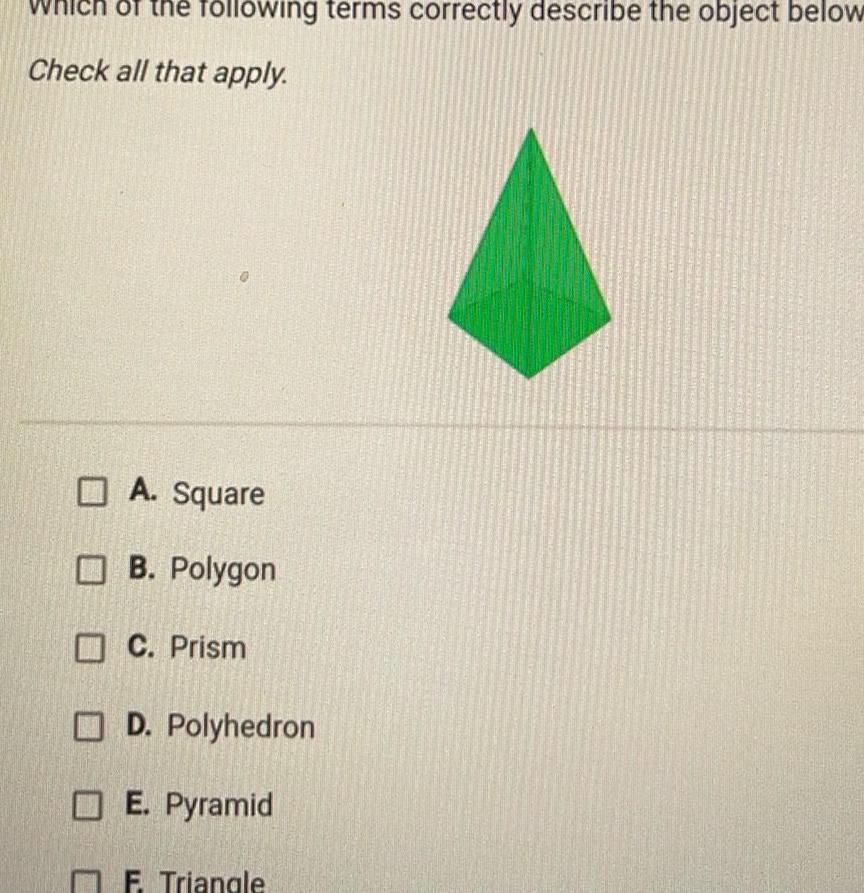
3D Geometryof the following terms correctly describe the object below Check all that apply A Square B Polygon C Prism D Polyhedron E Pyramid F Triangle
Geometry
Coordinate systemWhat is another name for the height of a prism OA Lateral face OB Altitude O O C Length O D Depth

Geometry
2D GeometryA is a solid consisting of two polygons that are parallel to each other and all points between them A prism B triangle OC pyramid D cube



Geometry
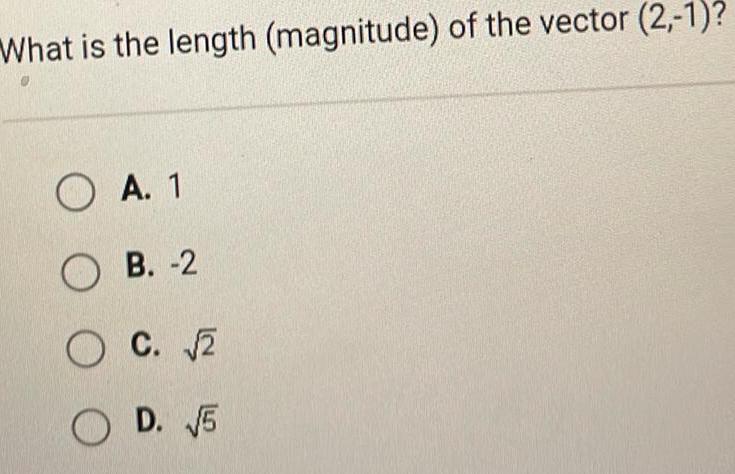
VectorsIf the dot product of two nonzero vectors V and V2 is zero what does this tell us A V is perpendicular to V OB V is a component of V2 C v is parallel to V OD V V
Geometry
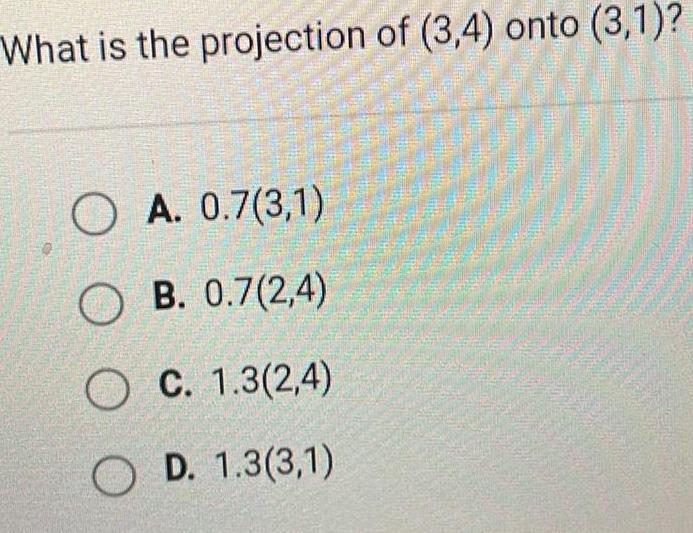
Coordinate systemWhat is the projection of 3 4 onto 3 1 OA 0 7 3 1 OB 0 7 2 4 OC 1 3 2 4 OD 1 3 3 1
Geometry
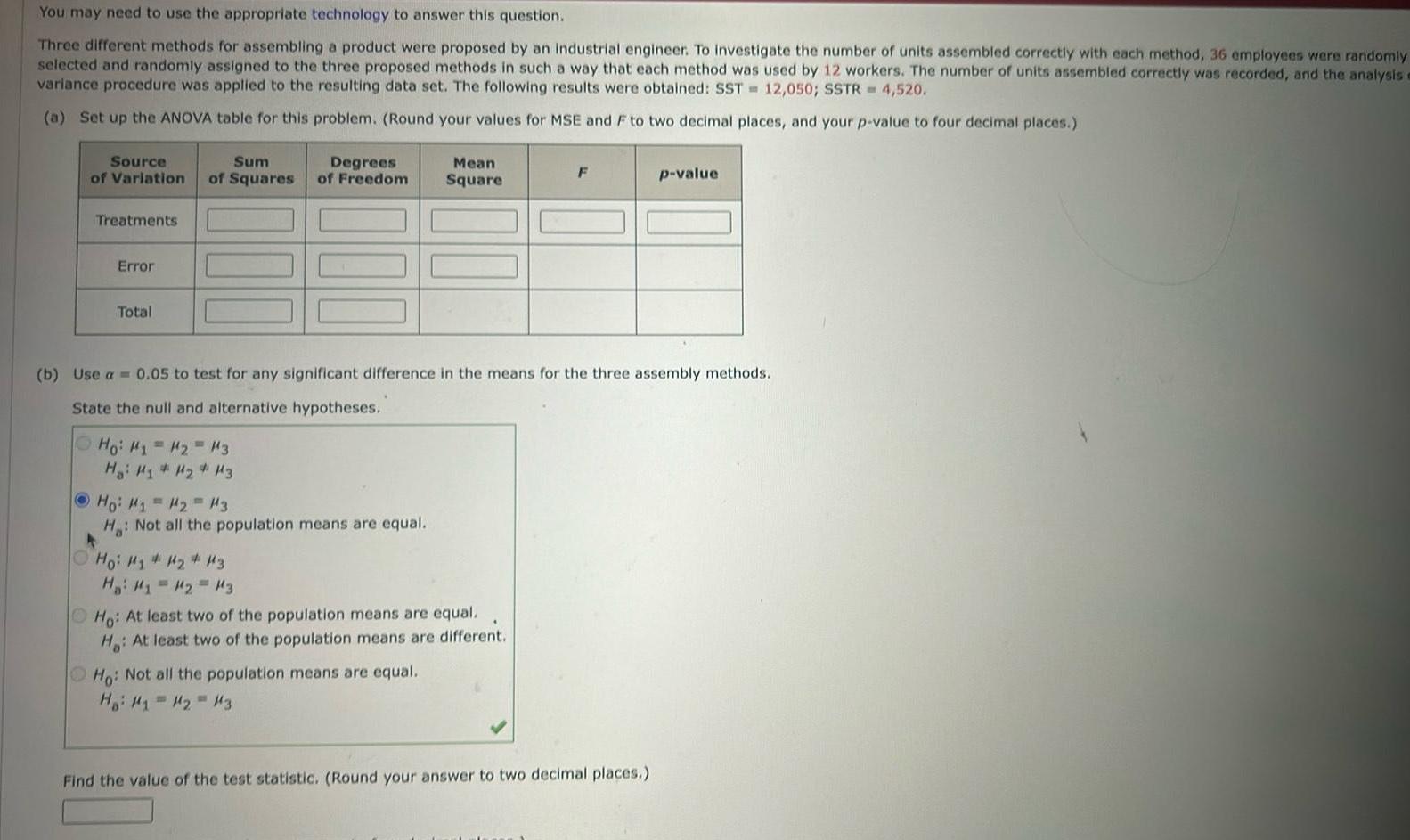
2D GeometryYou may need to use the appropriate technology to answer this question Three different methods for assembling a product were proposed by an industrial engineer To investigate the number of units assembled correctly with each method 36 employees were randomly selected and randomly assigned to the three proposed methods in such a way that each method was used by 12 workers The number of units assembled correctly was recorded and the analysis a variance procedure was applied to the resulting data set The following results were obtained SST 12 050 SSTR 4 520 a Set up the ANOVA table for this problem Round your values for MSE and F to two decimal places and your p value to four decimal places Source Sum Degrees of Variation of Squares of Freedom Treatments Error Total Ho H H H3 Ha H1 H H3 Ho M M M3 H b Use a 0 05 to test for any significant difference in the means for the three assembly methods State the null and alternative hypotheses Not all the population means are equal H i Minh Khay i t H H1 H 13 Mean Square Ho At least two of the population means are equal H At least two of the population means are different Ho Not all the population means are equal Hai H H H3 F p value Find the value of the test statistic Round your answer to two decimal places

Geometry
Coordinate systemWhat is the projection of 3 4 onto 3 1 O A 0 7 3 1 OB 0 7 2 4 O C 1 3 2 4 O D 1 3 3 1

Geometry
VectorsWhich of the following vectors are orthogonal to 1 5 Check all that apply A 1 5 B 10 2 C 5 1 D 2 5


Geometry
VectorsA n has both a magnitude and a direction 327 O A angle OB scalar C component O D vector

Geometry
VectorsLet v 8 4 and w 4 2 Which of the following is true Check all that apply A The y component of w is 2e2 B v w 40 C The x component of v is 4e D V 2W

Geometry
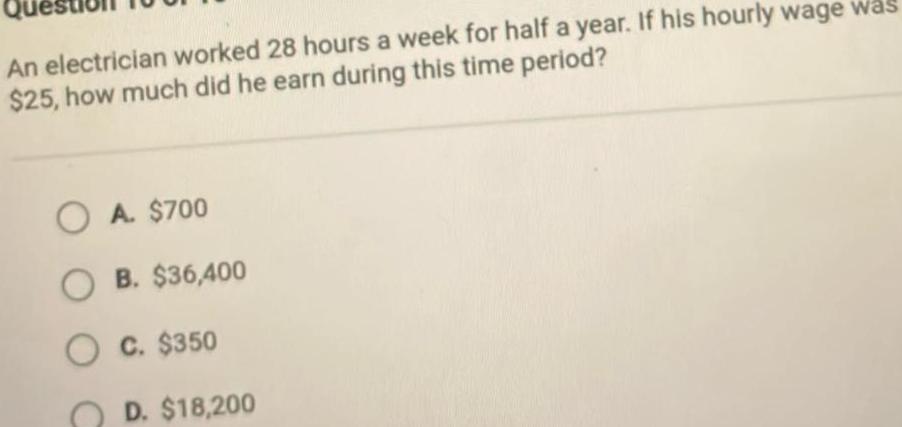
VectorsAn electrician worked 28 hours a week for half a year If his hourly wage was 25 how much did he earn during this time period OA 700 OB 36 400 O C 350 D 18 200
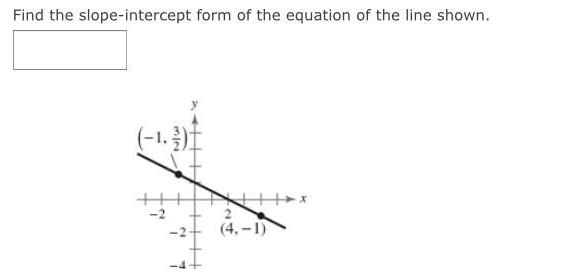
Geometry
Coordinate systemTroy worked for 3 hours and 15 minutes How should he write that on his time card A 3 25 OB 3 75 OC 3 15 OD 3 5

Geometry
2D GeometryIf y represents total earnings in dollars and x represents hours worked then which equation models the wages of someone who makes 11 50 an hour O A x 1150x B y 1150x C X 11 50x D y 11 50x

Geometry
AreaAn office administrator earns 16 an hour and she works 48 hours a week What is her weekly wage OA 768 OB 336 O C 64 OD 112
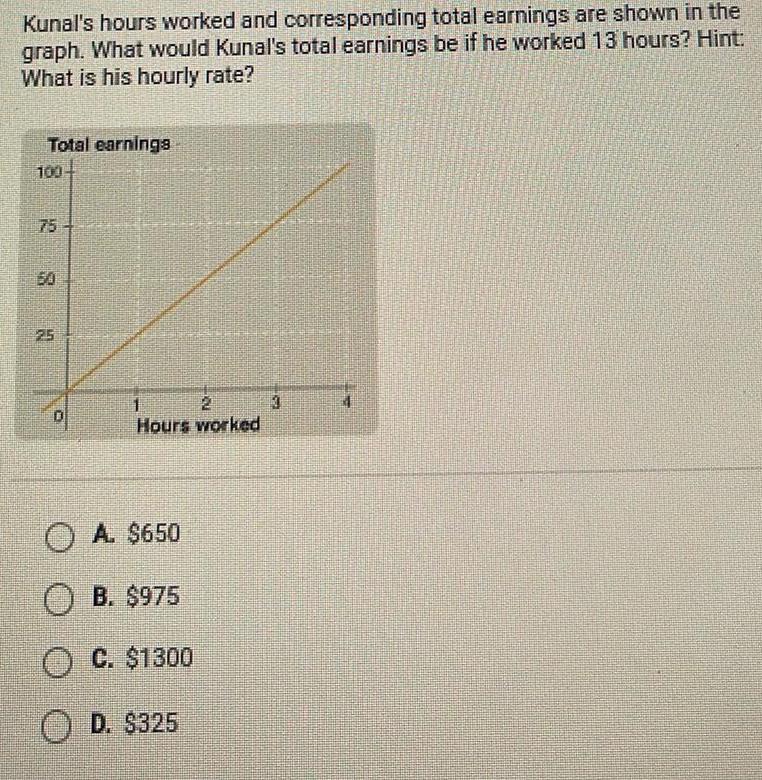
Geometry
2D GeometryKunal s hours worked and corresponding total earnings are shown in the graph What would Kunal s total earnings be if he worked 13 hours Hint What is his hourly rate Total earnings 75 150 25 D 1 2 Hours worked O A 650 B 975 O C 1300 D 325 3

Geometry
AreaLuke earned a salary of 48 048 last year How much did he earn a month OA 572 OB 4004 OC 6864 OD 924

Geometry
AreaMiguel earns 490 a week and he works 5 days a week What is his daily wage OA 495 OB 98 OC 70 OD 485
Geometry
2D GeometryA computer programmer earned 1043 a week last year What was her yearly salary A 55 279 B 56 322 C 53 193 D 54 236
Geometry
2D GeometryAfter finishing his shift a cashier wrote 2 25 under hours worked on his time card How long did he work O O A 2 hours and 25 minutes B 2 hours and 15 minutes C 2 hours and 50 minutes D 2 hours and 5 minutes

Geometry
3D GeometryMany simple three dimensional figures ale A weight B altitude C width D height E length
Geometry
3D GeometryOne can use two dimensional objects to build three dimensional objects A True B False

Geometry
2D GeometryThe and A length B height C weight D width E volume of many two dimensional figures can be measured

Geometry
2D GeometryWhen the Cartesian coordinate system is used to describe three dimensiona space one needs three axes These axes are typically called the and axes A y B V C Z D X E a

Geometry
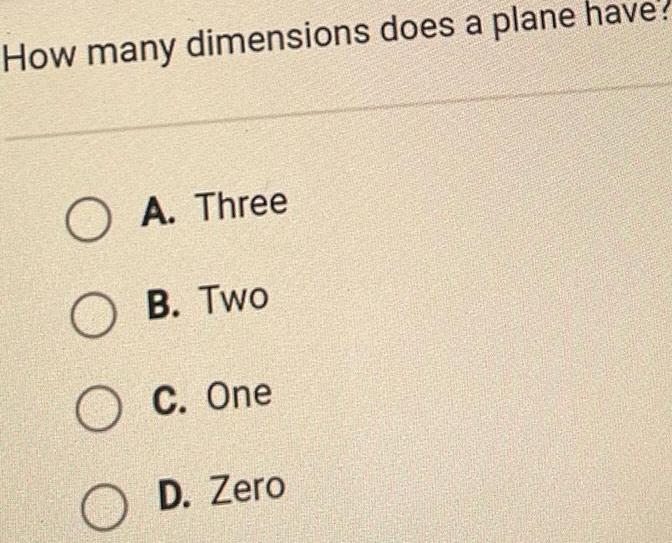
Coordinate systemWhich of the following is the standard notation for a point in a three dimensional Cartesian coordinate system A x y v OB x y z C x y z OD w x y
Geometry
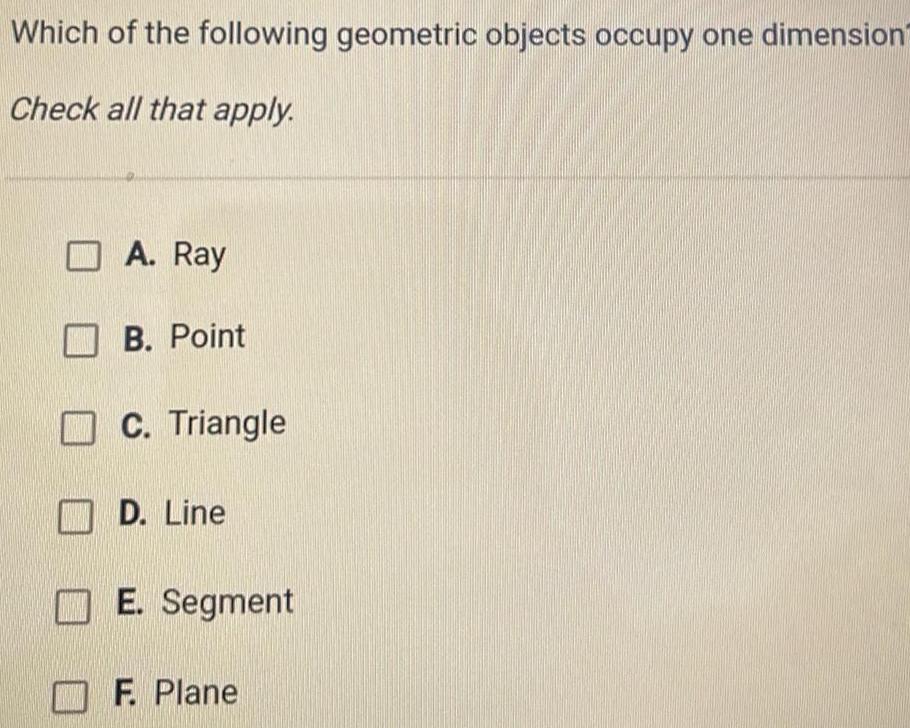
VectorsWhich of the following geometric objects occupy one dimension Check all that apply A Ray B Point C Triangle D Line E Segment F Plane
Geometry
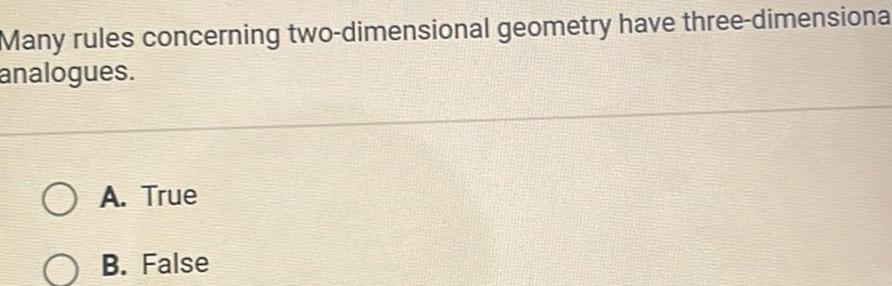
VectorsMany rules concerning two dimensional geometry have three dimensiona analogues OA True B False
Geometry
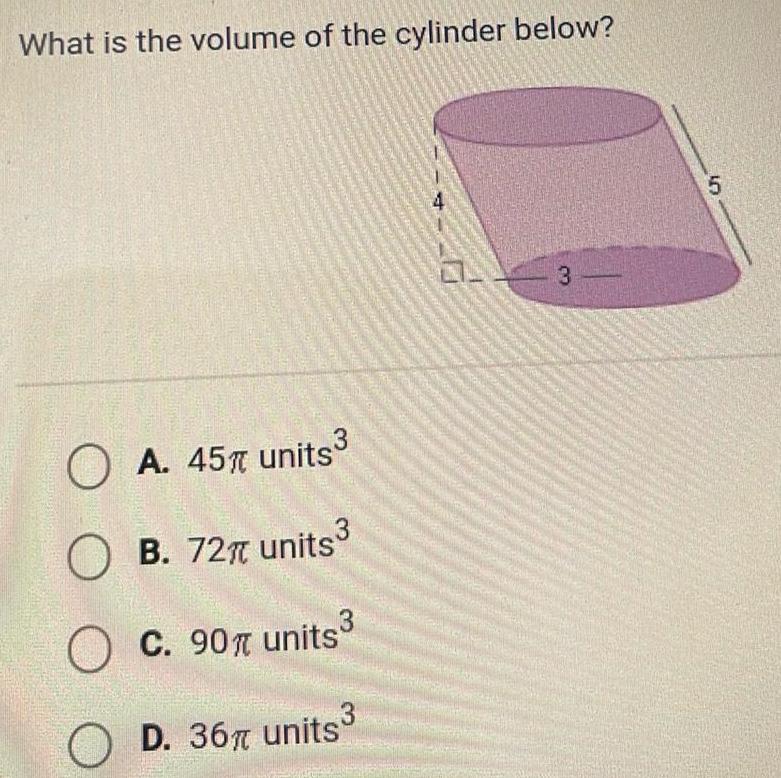
VectorsWhat is the volume of the cylinder below OA 45 units OB 727 units 3 C 90 units 3 3 O D 36 units 3 5
Geometry
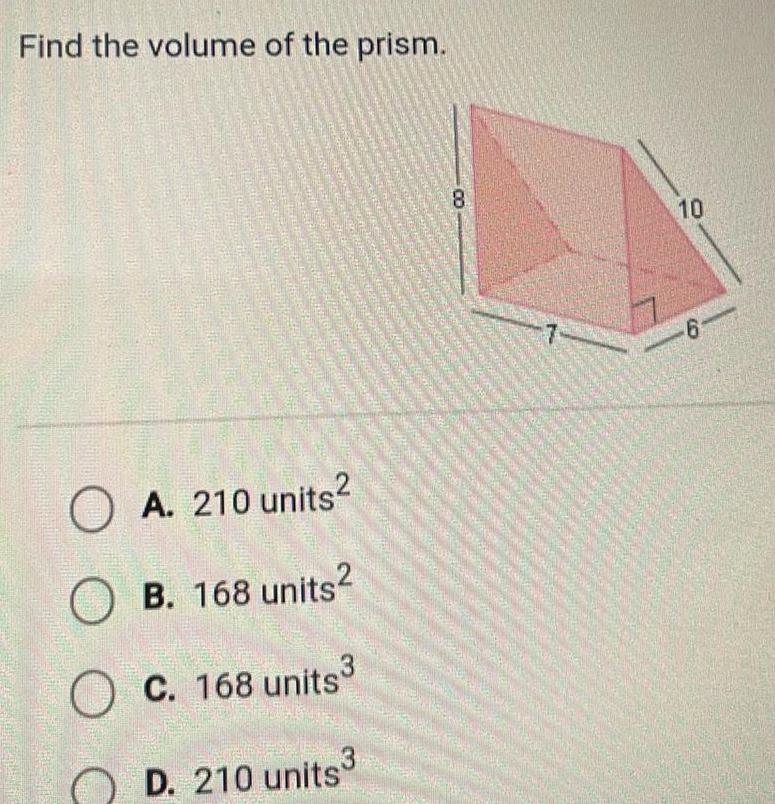
2D GeometryFind the volume of the prism www cs OA 210 units OB 168 units 3 OC 168 units C D 210 units3 8 7 10 6

Geometry
AreaWhat is the volume of the cylinder below A 64 units OB 1024 units OC 128 units OD 256 units 8
Geometry
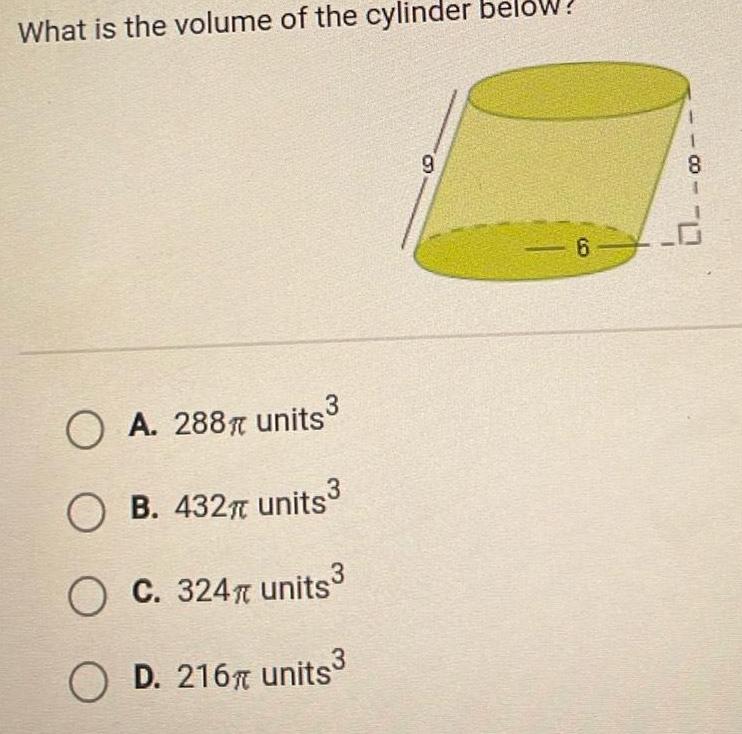
2D GeometryWhat is the volume of the cylinder below OA 288 units OB 432 units O C 324 units O D 216 units 9 6 8
