Solution of triangles Questions and Answers
Geometry
Solution of triangles2 The altitude of an equilateral triangle is 18 meters Find the perimeter of the triangle Perimeter of the triangle is 108 meters The

Geometry
Solution of trianglesDraw an equilateral triangle Draw the altitude of the triangle and label it a Let the shortest side of the right triangle be 1 unit long 2 30 13 Got 1 What is the length of the hypotenuse The length of the hypotenuse is 3 What is the length of a The length of a is 1
Geometry
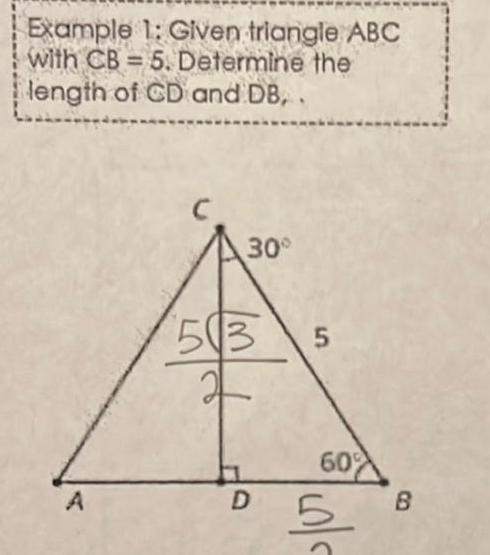
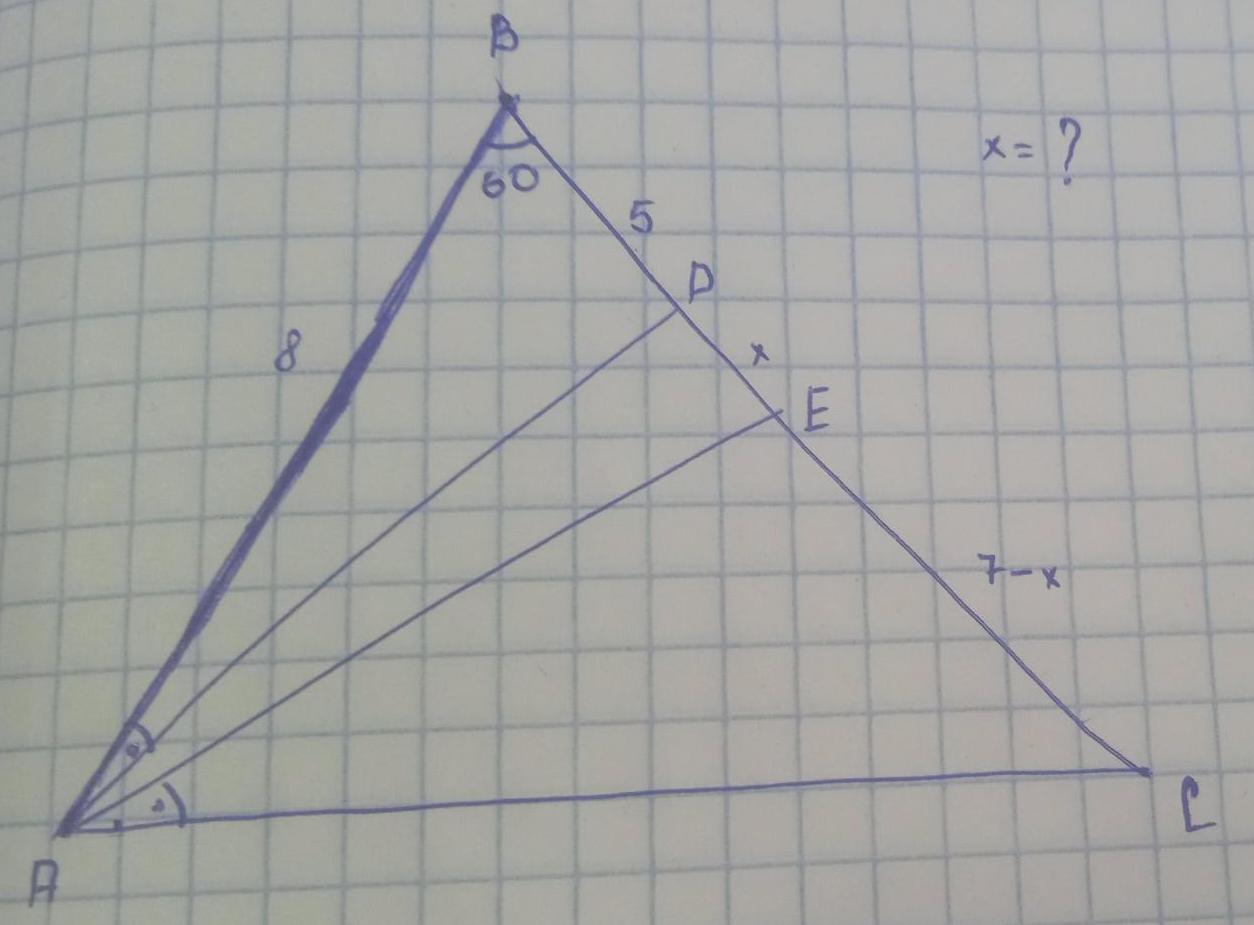
Solution of trianglesExample with CB length of CD and DB 1 Given triangle ABC 5 Determine the A 30 503 5 D 60 5 B

Geometry
Solution of triangles2 Solve the triangle by finding all missing sides and angles Round all values to the nearest hundredth 6 T 117 N
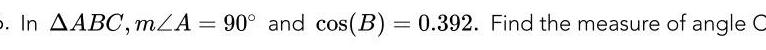
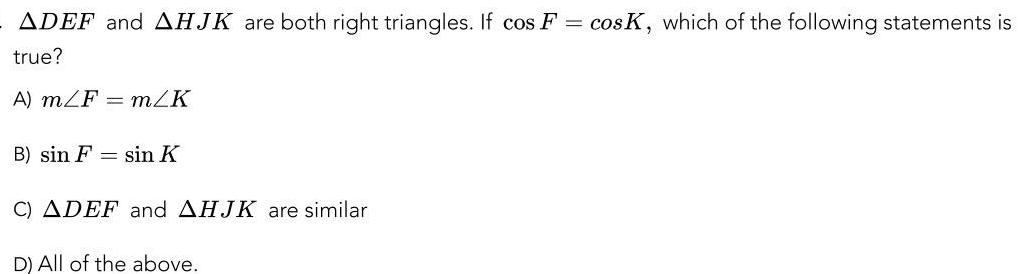
Geometry
Solution of trianglesADEF and AHJK are both right triangles If cos F cosK which of the following statements is true A m F m K B sin F sin K C ADEF and AHJK are similar D All of the above
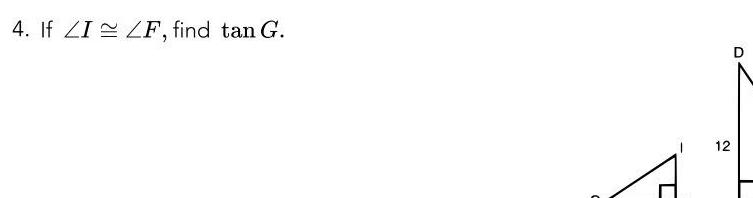
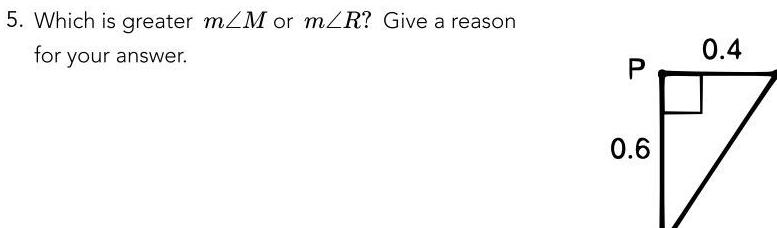
Geometry
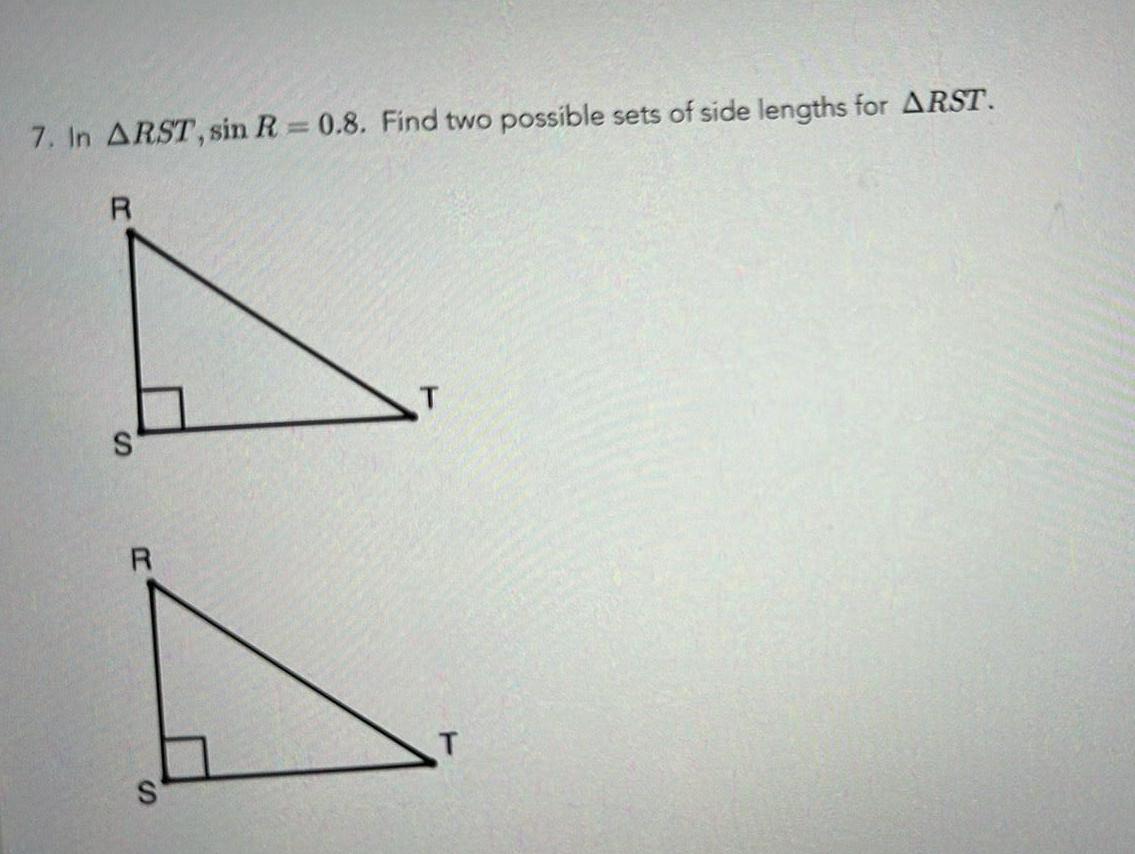
Solution of triangles7 In ARST sin R 0 8 Find two possible sets of side lengths for ARST S R S T T


Geometry
Solution of trianglesWe need a second quadrant angle se From the figure 0 ses x for which cos sin e cos e 2 Thus csc 0 2 for the following values 0 Use 0 2x Enter your answers as a comma separated list e
Geometry
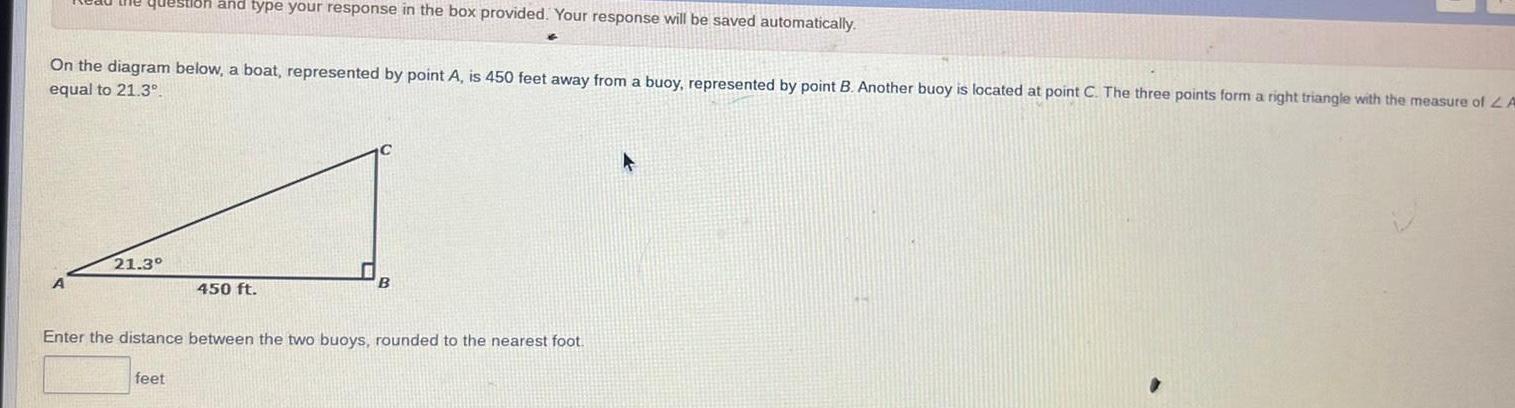
Solution of trianglesthe question and type your response in the box provided Your response will be saved automatically On the diagram below a boat represented by point A is 450 feet away from a buoy represented by point B Another buoy is located at point C The three points form a right triangle with the measure of A equal to 21 3 A 21 3 450 ft Enter the distance between the two buoys rounded to the nearest foot feet
Geometry
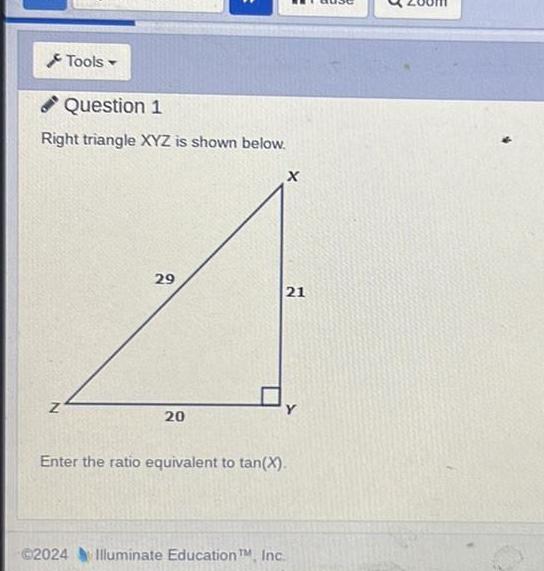
Solution of trianglesTools Question 1 Right triangle XYZ is shown below Z 29 20 X 21 Enter the ratio equivalent to tan X 2024 Illuminate Education TM Inc
Geometry
Solution of trianglesWhich of the following is NOT a valid Triangle Congruence Theorem A SSS B C ASA SAS
Geometry
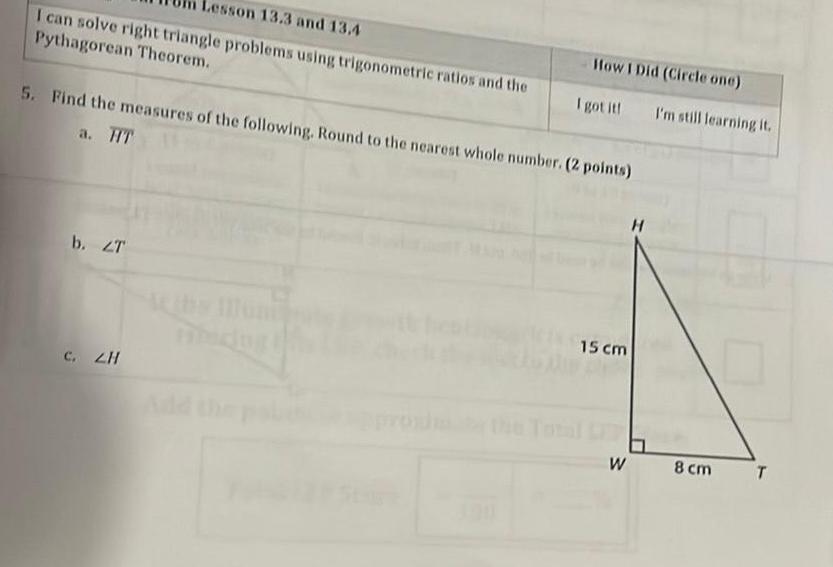
Solution of trianglesLesson 13 3 and 13 4 I can solve right triangle problems using trigonometric ratios and the Pythagorean Theorem 5 Find the measures of the following Round to the nearest whole number 2 points a HT b ZT How I Did Circle one I got it C ZH 15 cm H I m still learning it W 8 cm T
Geometry
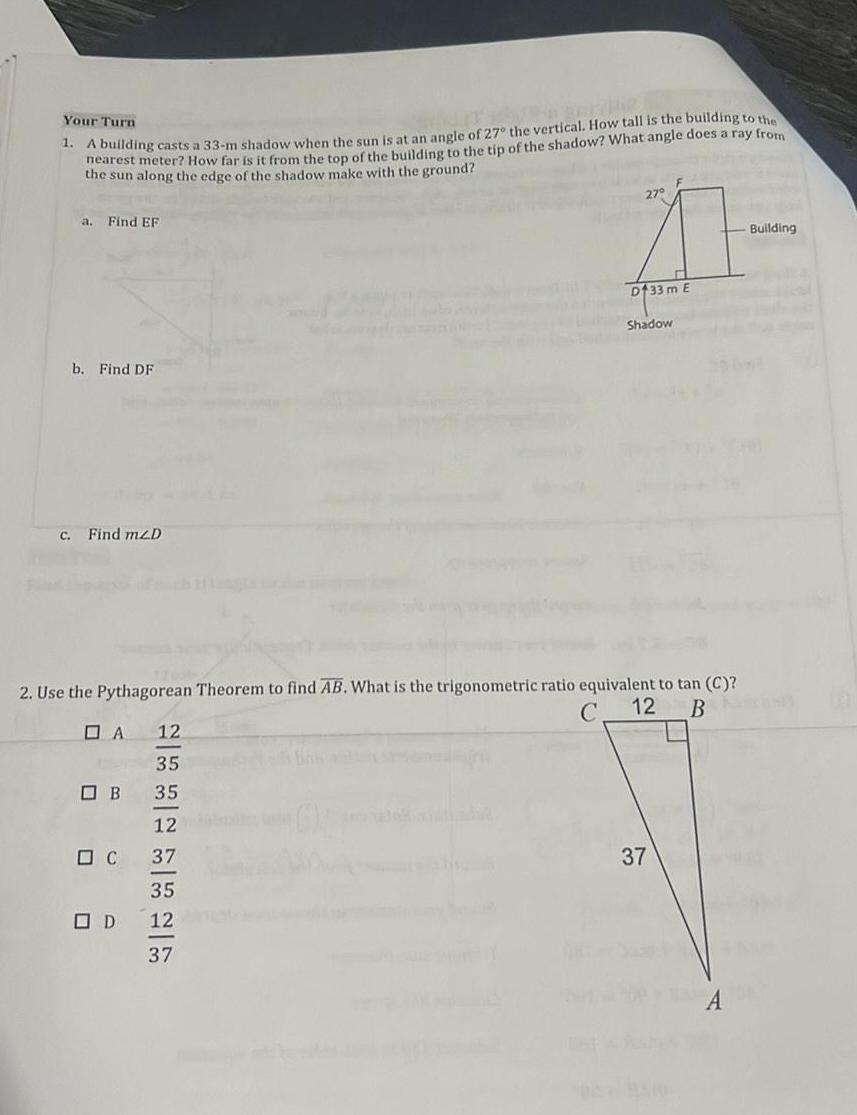
Solution of trianglesYour Turn 1 A building casts a 33 m shadow when the sun is at an angle of 27 the vertical How tall is the building to the nearest meter How far is it from the top of the building to the tip of the shadow What angle does a ray from the sun along the edge of the shadow make with the ground a Find EF b Find DF c Find m2D DA 2 Use the Pythagorean Theorem to find AB What is the trigonometric ratio equivalent to tan C C 12 B B C OD 12 35 35 12 37 27 11 D133 m E 35 12 37 Shadow 37 Building
Geometry
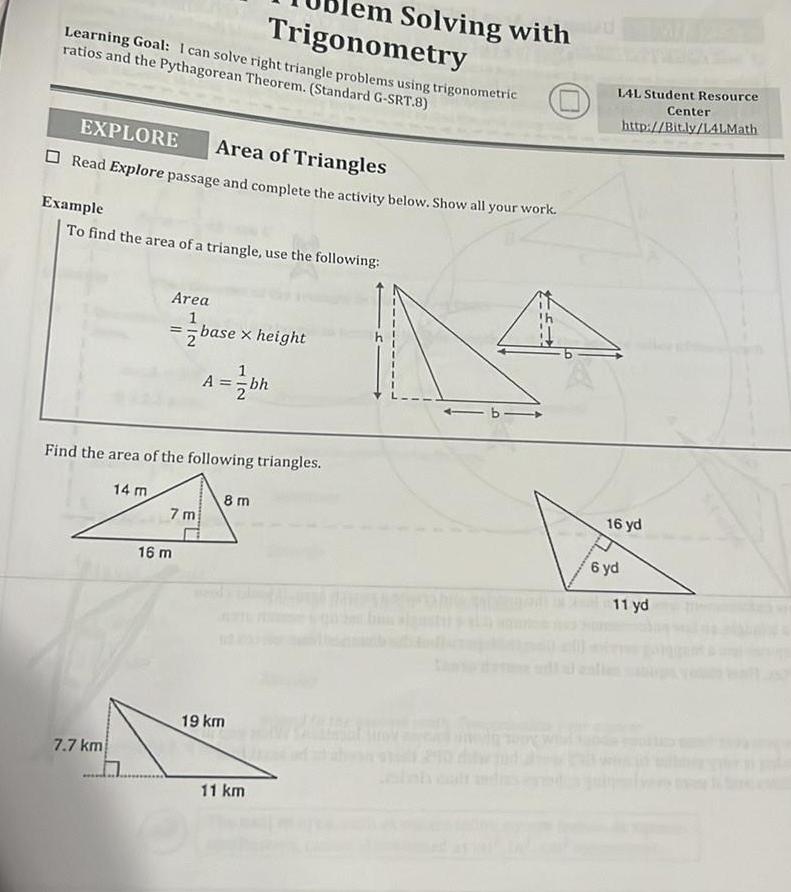
Solution of trianglesLearning Goal I can solve right triangle problems using trigonometric ratios and the Pythagorean Theorem Standard G SRT 8 EXPLORE Area of Triangles Read Explore passage and complete the activity below Show all your work Example To find the area of a triangle use the following 7 7 km 14 m lem Solving with Trigonometry Area 1 base x height 2 Find the area of the following triangles 8 m 20 7m A bh 16 m 19 km 11 km 1 L4L Student Resource Center http Bit ly LALMath 16 yd 6 yd 11 yd
Geometry
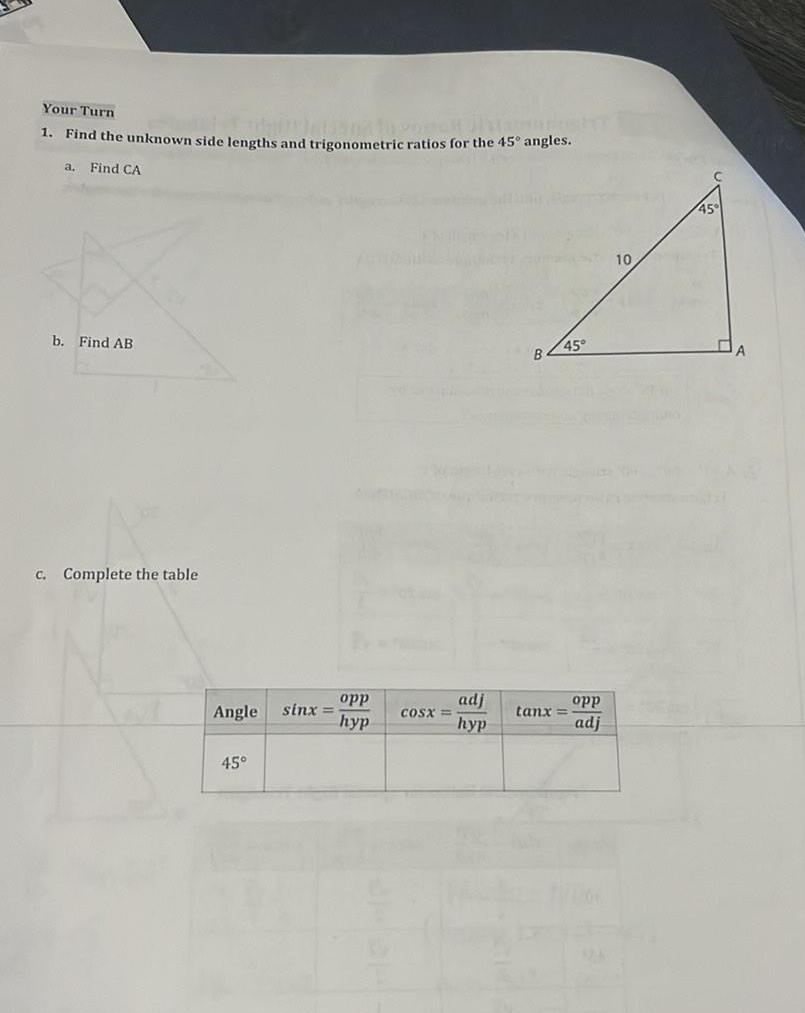
Solution of trianglesYour Turn Jhangos 1 Find the unknown side lengths and trigonometric ratios for the 45 angles a Find CA b Find AB c Complete the table Angle 45 sinx opp hyp COST adj hyp B 45 tant opp adj 10
Geometry
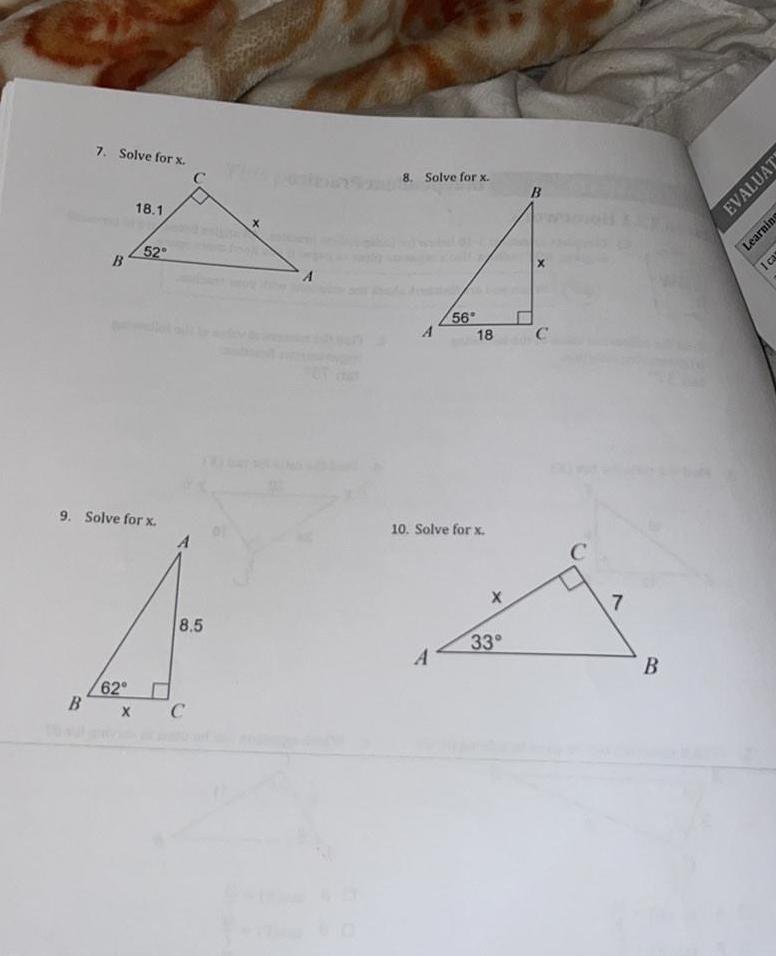
Solution of triangles7 Solve for x B 18 1 62 B X 52 9 Solve for x C 8 5 C A 8 Solve for x A 56 A 18 10 Solve for x 33 C C 7 B EVALUAT Learning I ca
Geometry
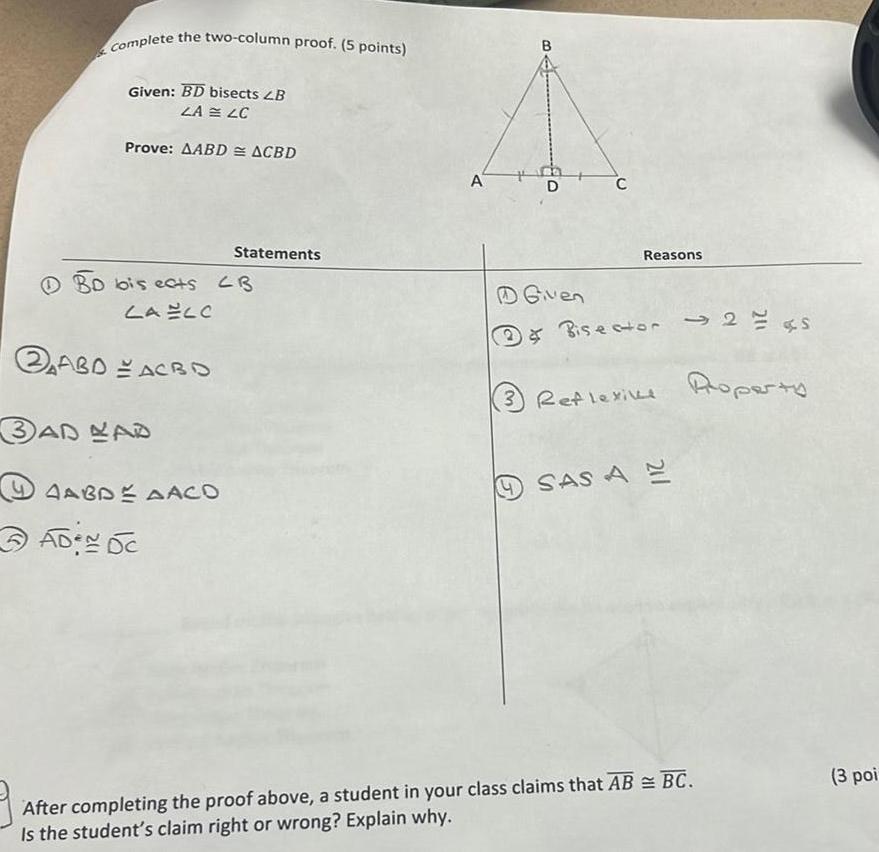
Solution of trianglesComplete the two column proof 5 points Given BD bisects LB ZA LC Prove AABD ACBD BD bis ects CB LA ELO ABD ACBO 3AD LAD AAGDE AACO Statements ADEN DC A D D Given C Reasons Bisector 2 s 3 Reflexive Roperty SAS AE After completing the proof above a student in your class claims that AB BC Is the student s claim right or wrong Explain why 3 poi


Geometry
Solution of triangles35 DEVELOPING PROOF Complete the proof of the Third Angles Theorem GIVEN LA LD LB LE PROVELC LF Statements 1 LA LD LB LE 2 m m m m 3 mLA mLB mLC 180 mLD mLE mLF 180 4 mLA m B m C mLD mLE mLF 5 m D m E m C mLD mLE mLF 6 m C m F 7 A B 1 2 3 Reasons 4 5 C D 6 7 Def of s E F
Geometry
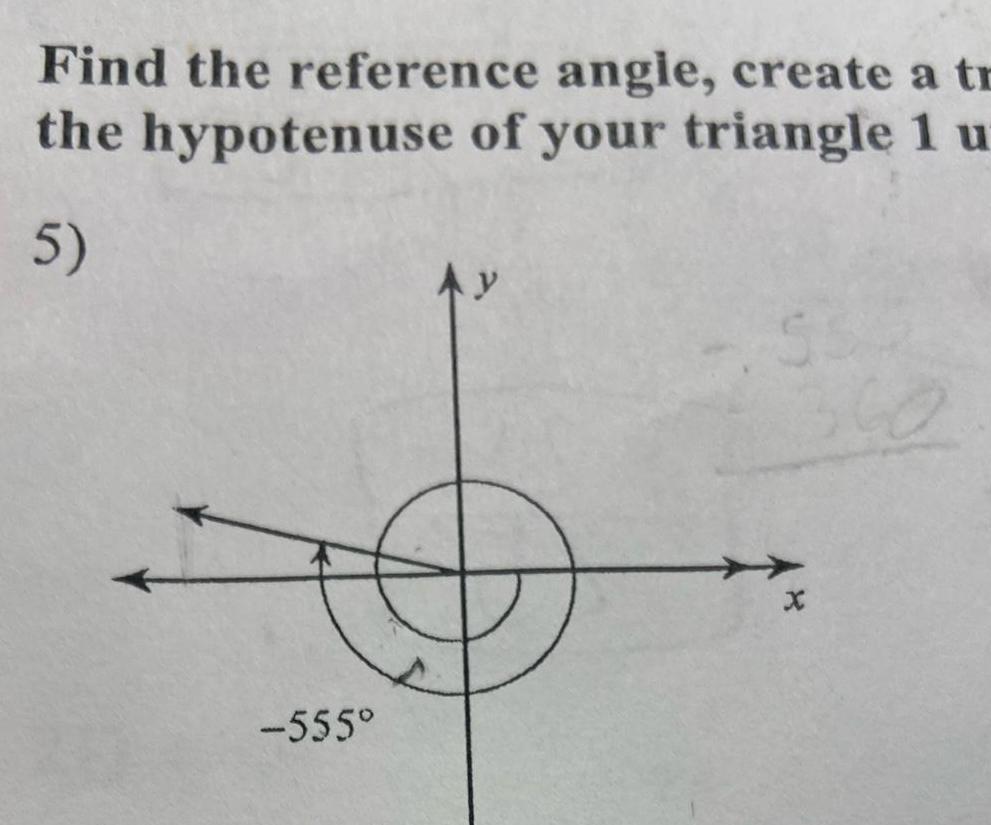
Solution of trianglesFind the reference angle create a tr the hypotenuse of your triangle 1 u 5 555 y

Geometry
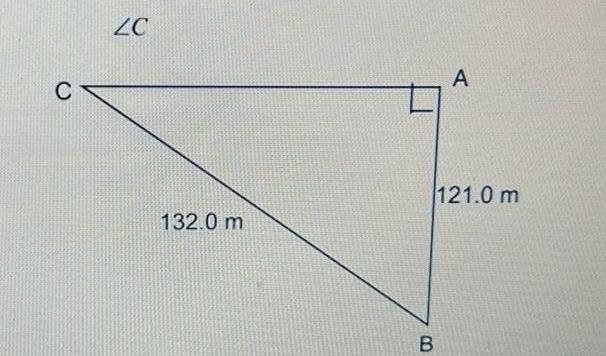
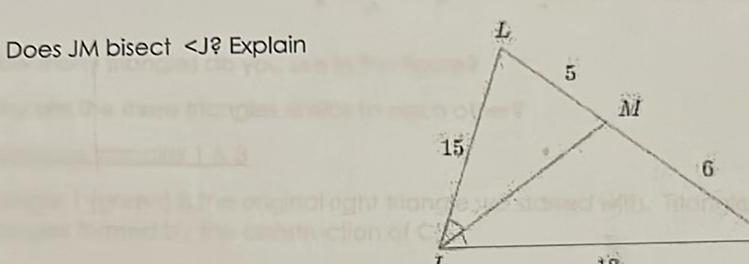
Solution of trianglesGeometry 8 Tell whether a triangle can have sides with the given I a 11 17 28 b 3 10 11 9 Describe the possible lengths of the third side of the triangle given the lengths of the other two sides a 16 inches 20 inches b 8 meters 12 meters c 5 feet 14 feet 10 List the angles of the triangle in order from smallest to largest a b 21yd D V 8 yd 15yd F B 57 E 77 46 Q 11 List the sides of the triangle in order from smallest to largest b a C 10 cm 12 cm H 95 R 419 6 cm 44 P F C C U 20 ft 3 1259 W 24 f 219 21 ft K L V
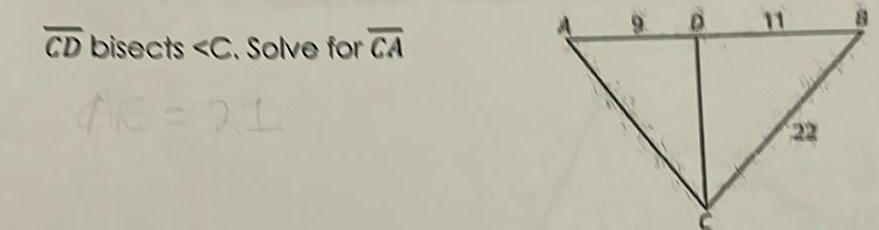

Geometry
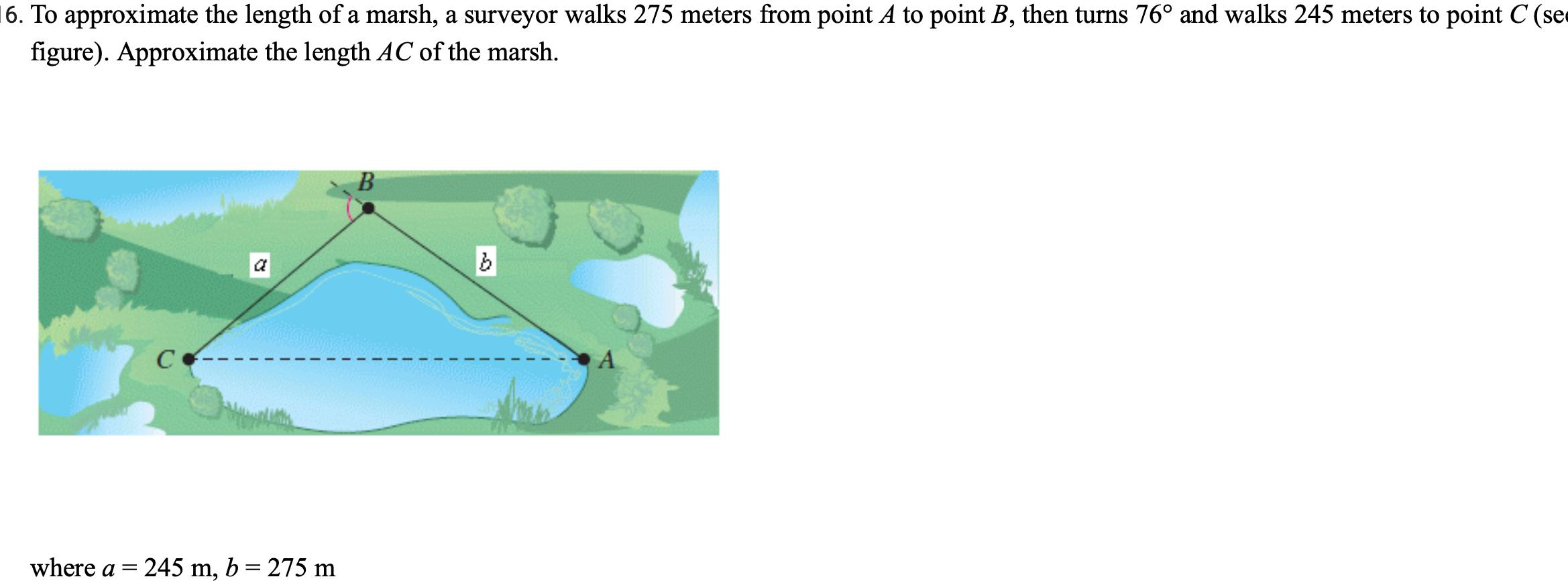
Solution of triangles6 To approximate the length of a marsh a surveyor walks 275 meters from point A to point B then turns 76 and walks 245 meters to point C se figure Approximate the length AC of the marsh where a CO a 245 m b 275 m B b A

Geometry
Solution of triangles11 Use the Law of Sines to solve if possible the triangle If two solutions exist find both Round your answers to two decimal places A 60 a 13 b 11 6 B 50 6 C 69 40 c 14 05 B 29 C 91 c 13 B 69 40 C 50 6 c 11 6 B 91 C 29 c 14 05

Geometry
Solution of triangles5 Given C 116 a 13 9 and c 9 3 use the Law of Sines to solve the triangle if possible for the value of b If two solutions exist find both Rou your answer to two decimal places b 1 99 and 6 31 b 1 06 and 6 44 b 4 43 not possible b 7 68

Geometry
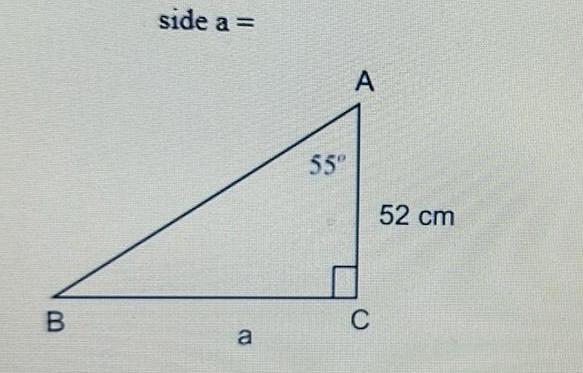
Solution of triangles7x 15 12 in x 28 4x 3 zoom in 3 Find x given this triangle Find a and b given this triangle You c wer like a 38 in b 5

Geometry
Solution of triangles3 Determine whether the Law of Sines or the Law of Cosine is needed to solve the triangle Then solve the triangle a 8 c 5 B 40 Law of Sines A 102 34 C 37 66 b 5 26 O Law of Sines No solution Law of Cosines A 37 66 C 102 34 b 5 26 Law of Sines A 37 66 C 102 34 b 5 26 Law of Cosines A 102 34 C 37 66 b 5 26

Geometry
Solution of triangles24 Given that KM is the perpendicular bisector JL prove that JK LK 24 Given that KM is the perpendicular bisector of JL prove that JK LK Use the word phrase bank to complete the paragraph proof 1 KM is the perpendicular bisector of JL KML and 2 are both of perpendicular lines KM KM by the Triangle QTR Triangle SRT by the Therefore JK LK because congruent A Reflexive Property B Corresponding C Alternate Interior D Angle Angle Side Congruence E Angle Side Angle Congruence F Side Angle Side Congruence 5 6 4 3 by definition of a bisector G Right H Congruent J KMJ K MLK L JK LK M JM LM Theorem Langles by definition parts of congruent triangles are
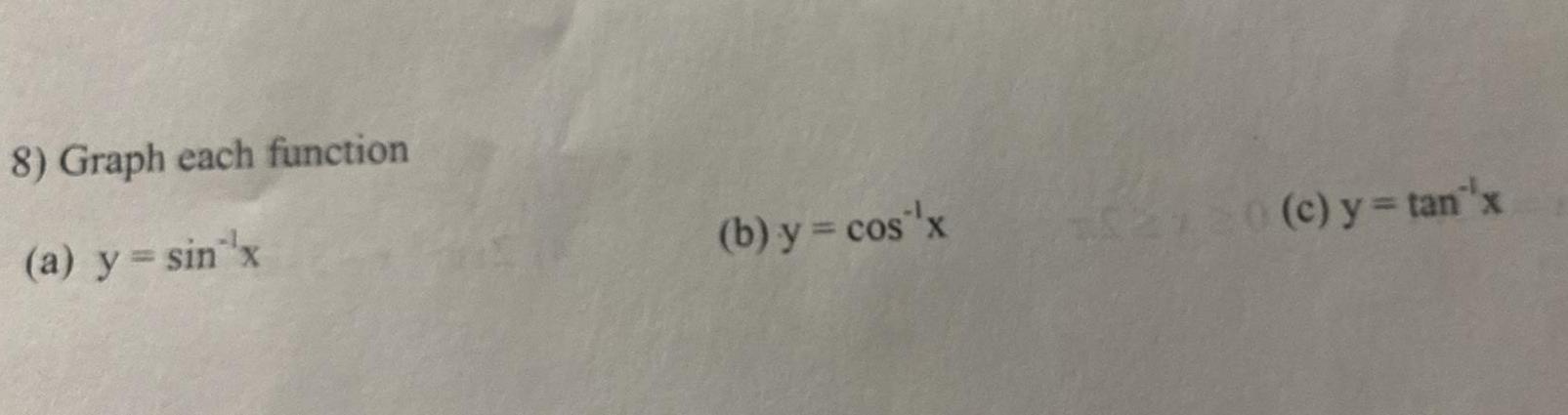

Geometry
Solution of trianglesIn 6 Write a triangle congruency statement and state the theorem SSS SAS ASA AAS you can use to prove the triangles congruent 6 A B E C D Triangle Congruence Statement Reason

Geometry
Solution of trianglesUse the congruency statement to state corresponding congruent parts 11 ARUTATSR ZURTE ZU RU RT 18

Geometry
Solution of triangles2 Given C 122 a 25 and c 18 use the Law of Sines to solve the triangle if possible for the value of b If two solutions exist find both Round answer to two decimal places b 13 97 O not possible O b 15 34 and 19 86 O b 8 72 and 12 09 b 9 65
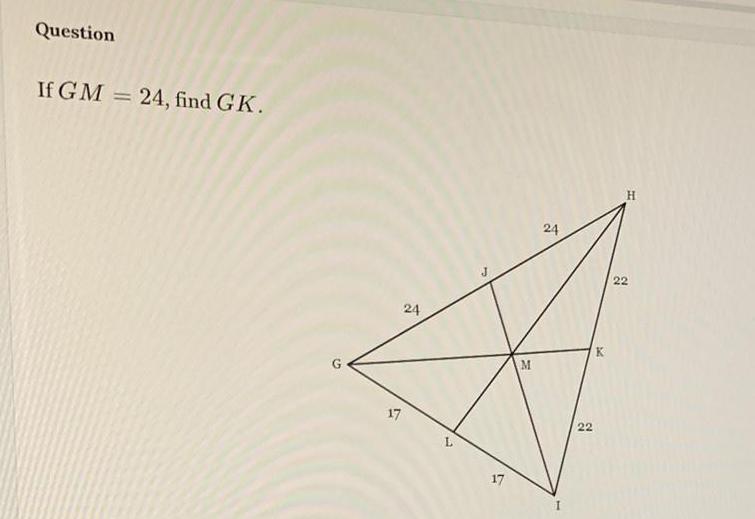
Geometry
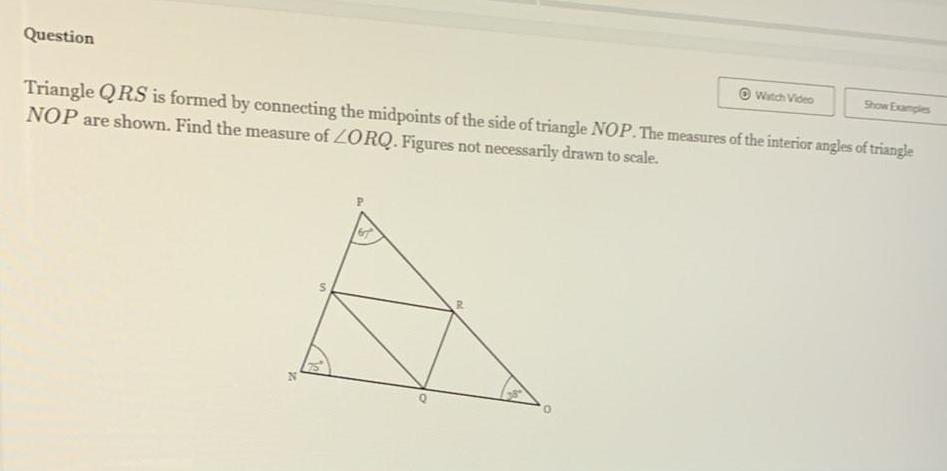
Solution of trianglesQuestion Triangle QRS is formed by connecting the midpoints of the side of triangle NOP The measures of the interior angles of triangle NOP are shown Find the measure of ZORQ Figures not necessarily drawn to scale in R 0 Watch Video Show Examples
Geometry
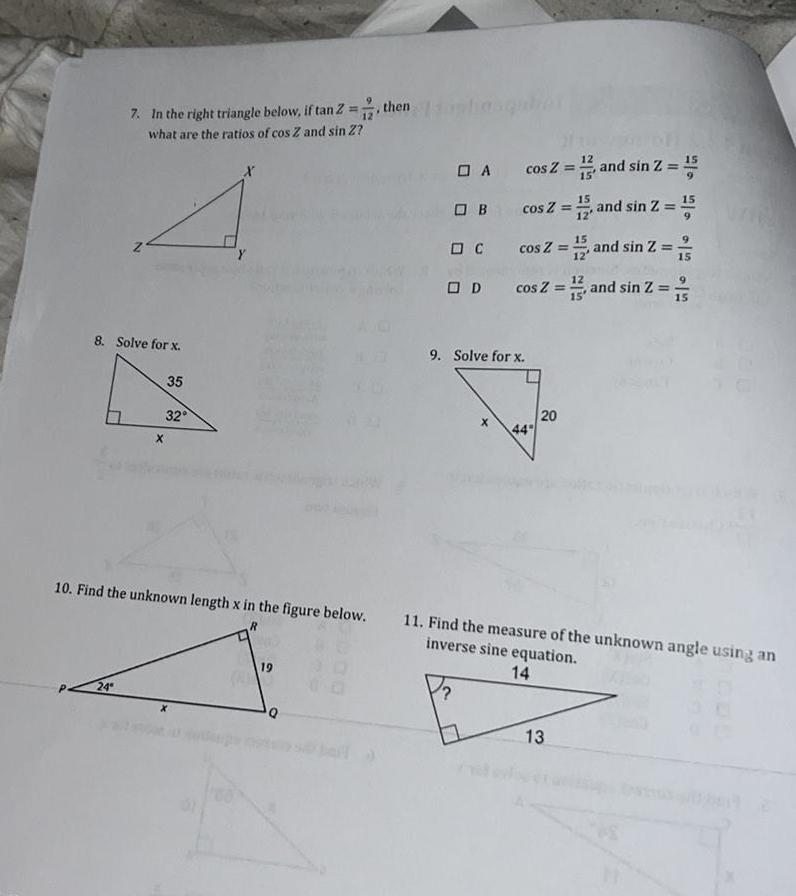
Solution of triangles7 In the right triangle below if tan Z what are the ratios of cos Z and sin Z N 8 Solve for x 24 X 35 32 X 19 then Q 15 A cos Z and sin Z OB cos Z 1 and sin 2 15 cos Z 15 and sin Z 2 12 15 cos Z C OD 9 Solve for x 44 20 10 Find the unknown length x in the figure below 11 Find the measure of the unknown angle using an inverse sine equation 14 12 13 15 and sin Z 2

Geometry
Solution of trianglesEXPLAIN 1 Applying Relationships in Special Right Triangles Read Explain 1 and complete Your Turn 1 4 adapted from Lesson 13 3 Show all your work Side length Relationships in a 45 45 90 Right Triangle The hypotenuse is 2 time as long as each leg for any sized right triangle with 45 45 90 interior angles 60 45 2x x 2 Side length Relationships in a 30 60 90 Right Triangle The hypotenuse is twice as long as the shorter leg and the longer leg is 3 times as long as the shorter leg for any sized right triangle with 30 60 90 interior angles 30 45 x 3 Example If the hypotenuse has a length of 3 2 ft then x 3 The height and width are 3 ft long Example If the hypotenuse has a length of 6 ft then x 3 The height is 3 3 ft and the width is 3 ft If the hypotenuse is 6 feet then by rule 2x 6 Divide 2 on both sides makes x 3

Geometry
Solution of trianglesLesson 13 1 Homework 1 Z EVALUATE HW 3 3 Find the ratio for tan X X Find the numerical value of the following trigonometric function tan 37 0 15 12 A tan 0 B 5 Which equation can be used in solving for 07 A B tan 8 C tan 0 D tan 0 11 Complete problems 1 10 below for independent practice All angles below are in terms of degrees NOT radians Use a separate piece of paper if you need more space When you are finished check the solutions with your teacher 1W E Independent Practice 9 8 2 Find the numerical value of the following trigonometric function tan 73 4 Find the ratio for tan X 30 X Z 24 A 7 L 6 Which equation can be used in solving for 8 0 Y 18 A tan 0 B tan 0 0 tan 8 D tan 0 11 E B

Geometry
Solution of trianglesopposite adjacent and hypotenuse At the same time the new vocabulary words cross reference How do you w it all organized in your head With memory techniques Below is an example of how acronyms are used to help Within two lessons you have learned a lot of new vocabulary words such as sine cosine tangent inverse remember and organize new knowledge Memory Technique Acronyms Acronyms are words formed from the first letters from a list of words Use an acronym to remember trigonometric ratios Memory Technique for Trigonometric Ratios SOHCAHTOA The acronym SOHCAHTOA pronounced soh cah toa comes from the first letters from the list of words sine opposite hypotenuse cosine adjacent hypotenuse tangent opposite adjacent Get it It is to help you remember the three trig ratios and how to set up the fraction such as what side belongs in the numerator or denominator Fill in the blank 0 O A S C T H H CH Graphic Organizer Use this graphic being asked to angle Examp Fir This is to help you remember Sine is opposite over hypotenuse Cosine is adjacent over hypotenuse Tangent is opposite over adjacent Imagine if you didn t know the acronym SOHCAHTOA You would be saying Sine is opposite over potenuse Cosine is adjacent over hypotenuse Tangent is opposite over adjacent over and over and over until you remembered it Optional It may even help if you color it in to remember the acronym Trigonometric cha SOUCA IO 1
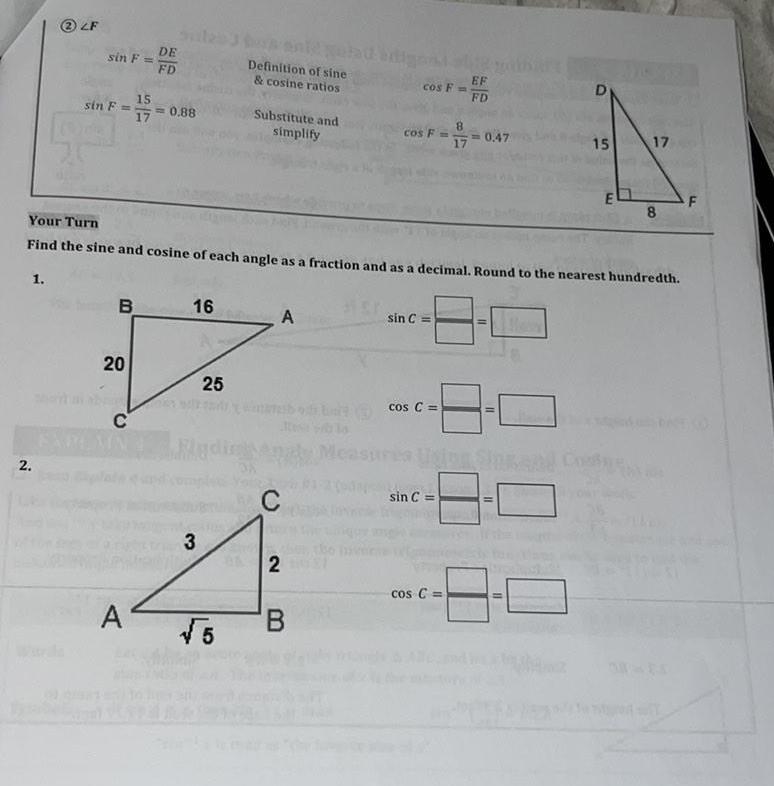
Geometry
Solution of triangles1 2LF 2 sin F sin F B 20 C DE FD 15 17 0 88 A 16 3 25 Definition of sine cosine ratios 5 Substitute and simplify Your Turn Find the sine and cosine of each angle as a fraction and as a decimal Round to the nearest hundredth A C 2 cos F B cos F sin C cos C sin C 17 cos C EF FD 0 47 11 11 11 D 15 Cos E 17 8 F

Geometry
Solution of trianglesIn the following example you will learn how to apply the inverse tangent function to find an unknown a Example Apply the tangent ratio to find unknown angles Find the measure of the indicated angle Round your answer to the nearest tenth of a degree What is mLA BC tan A CA tan A A tan mzA What is m2B A 27 8 tan B tan B B tan 19 2 Find m2K 36 H 1 CA BC 36 19 36 m2B 62 2 Definition of tangent ratio Substitution Property Definition of an Inverse Tangent 1 use calculator Calculate tan Definition of tangent ratio Substitution Property Definition of an Inverse Tangent Calculate tan use calculator 36 in Your Turn Find the measure of the indicated angle Round your answer to the nearest tenth of a degree 1 Find m2 K 19 in Dc 93 Graphic Organize Use this graphic org you are being aske side or angl

Geometry
Solution of trianglesMP and NP are midsegments of AJKL Your Turn 1 Find mzJLK MP LK LJMP LJLK mzJMP mzJLK 105 mzJLK 2 Find JL 2PN JL 2 39 JL 78 JL 2QR MN 2 4n 9 14n 8n 18 14n 18 6n 3 n MN 14n Triangle Midsegment Theorem Corresponding Angles Theorem Definition of Congruent Angles Substitution Property MN 14 3 MN 42 Triangle Midsegment Theorem Substitution Property EXPLAIN 2B Using the Triangle Midsegment Theorem Read Explain 2B and complete Your Turn 3 4 Adapted from Lesson 8 4 Show all your work Example M 1 Find MN Simplify Triangle Midsegment Theorem Substitution Property Distributive Property Subtraction Property of Equality Division Property of Equality Given 105 M H Substitution Property Simplify Q P P 39 N 4n 9 9 14n R N