Functions Questions and Answers
Math - Others
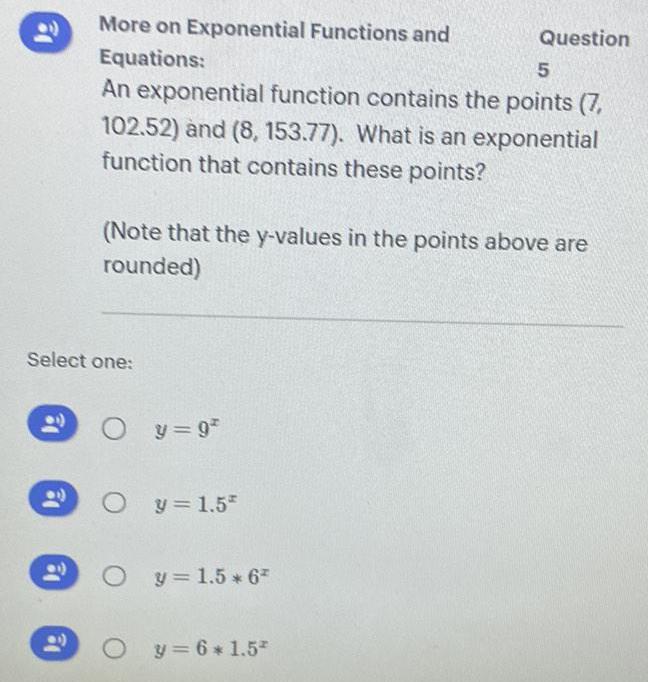
FunctionsAn exponential function contains the points (7, 102.52) and (8, 153.77). What is an exponential function that contains these points? Select one: (Note that the y-values in the points above are rounded)
y=9²
y = 1.5
y = 1.5 * 6²
y = 6*1.5*
Math - Others
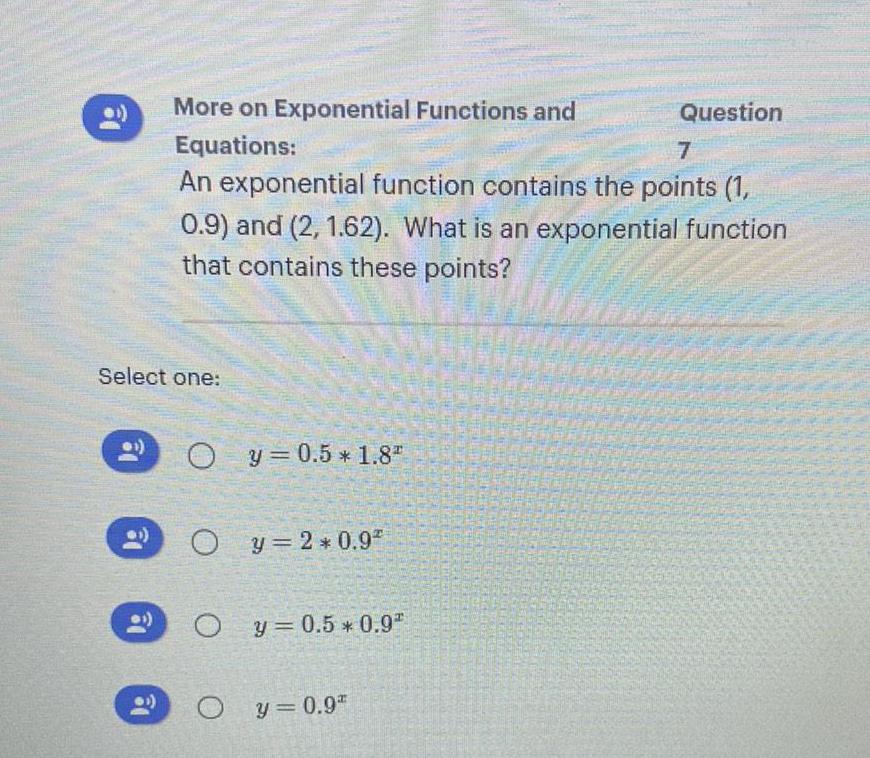
FunctionsAn exponential function contains the points (1,0.9) and (2, 1.62). What is an exponential function
that contains these points?
y 0.5 * 1.8"
y=2*0.9²
y = 0.5 * 0.92
y = 0.9
Math - Others
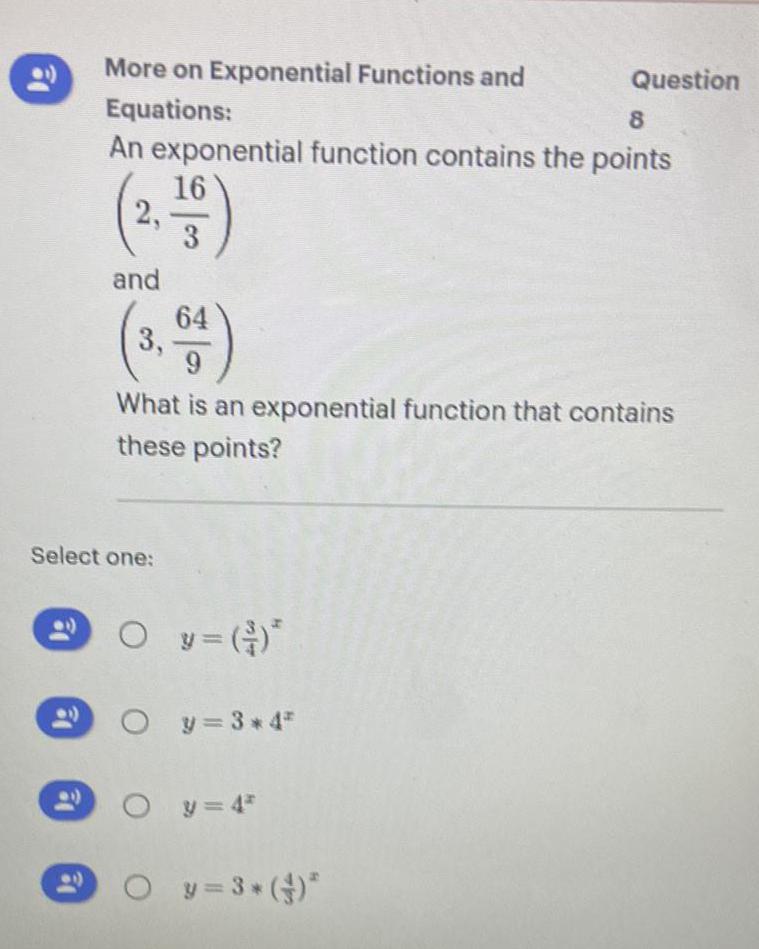
FunctionsAn exponential function contains the points (2,16/3) and (3, 64/9)
What is an exponential function that contains these points?
Select one:
y=(3/4)*
y=3*4^x
y = 4^x
y=3* (4/3)^x


Math - Others
FunctionsFactor each polynomial completely. If a polynomial cannot be factored, write "prime".
a) t² + 4t - 12
List possible combinations:
Factored form:
b) a²-a-12
List possible combinations:
Factored form:

Math - Others
Functionsf (x) is transformed from y =x^3 by shift 1 units to the right, reflect about the y-axis, vertical stretch by a factor of 2, and shift 3 units up.
Find the equation for f(x)
f(x) = 2 (-2+3)³ +1
f(x) = -2(x+3)³ + 1
f(x)=2(-x-1)³ +3
f(x) = -2(x+1)³ +3
f(x) = -2(x-1)³ +3
f(x) = 2 (-x+1)³ +3

Math - Others
FunctionsDetermine whether the following function is even, odd, or neither.
f(x) = 2x² - 3
![A table for f (x) is given below.
x -4 -2 0 2 4
f(x) 5 6 8 10 14
Complete the following tables. [Hint: Be sure to list the x values from least to greatest.]
x A B C D E
h(x)=f(x-3) F G H I J
A=
B=
C=
D=
E=
F=
G=
H=
I=
J=](https://media.kunduz.com/media/sug-question/raw/84312581-1657382186.3684218.jpeg?w=256)
Math - Others
FunctionsA table for f (x) is given below.
x -4 -2 0 2 4
f(x) 5 6 8 10 14
Complete the following tables. [Hint: Be sure to list the x values from least to greatest.]
x A B C D E
h(x)=f(x-3) F G H I J
A=
B=
C=
D=
E=
F=
G=
H=
I=
J=

Math - Others
FunctionsLet f(x) = 4x-6 and g(x) = 5x². Find the domain of (f+g)(x).
Select one:
a. The domain of f + g is the set of all real numbers except x = 0.
b. The domain of f + g is the set of all x ≤0.
c. The domain off + g is the set of all x ≥ 0.
d. The domain of f + g is the set of all real numbers.
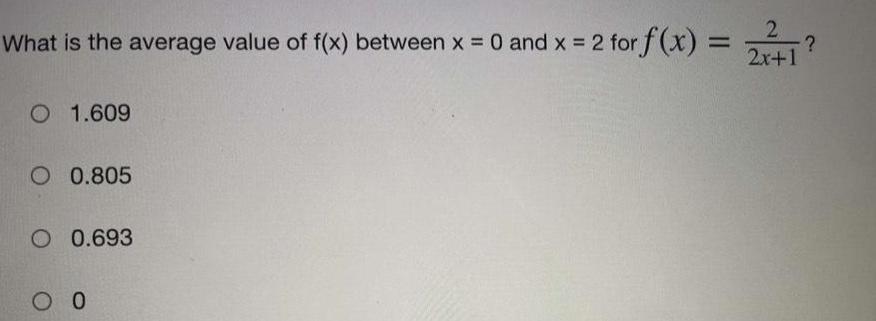
Math - Others
FunctionsWhat is the average value of f(x) between x = 0 and x = 2 for f(x) =2/2x+1
1.609
0.805
0.693
0
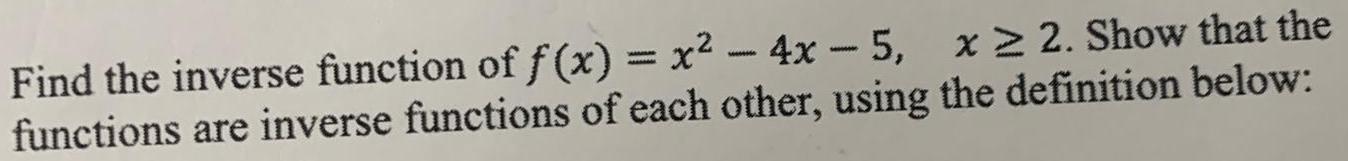
Math - Others
FunctionsFind the inverse function of f(x) = x² - 4x-5, x ≥ 2. Show that the functions are inverse functions of each other, using the definition below:
Math - Others
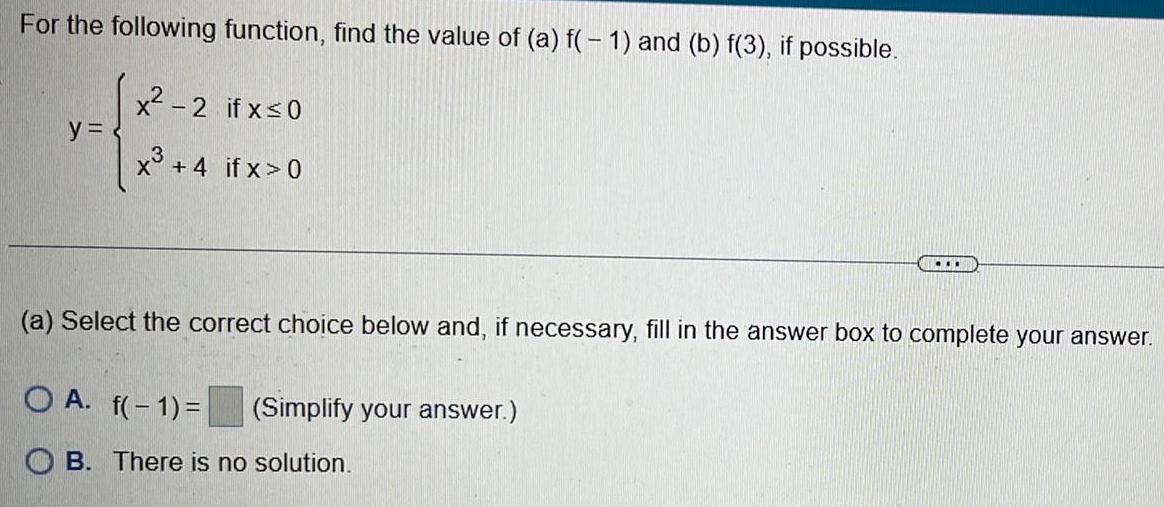
FunctionsFor the following function, find the value of (a) f(-1) and (b) f(3), if possible.
y= x²-2 if x ≤0
x³ +4 if x > 0
(a) Select the correct choice below and, if necessary, fill in the answer box to complete your answer.
A. f(-1) =
B. There is no solution.
(Simplify your answer.)

Math - Others
FunctionsFor the following functions: answer the all these
a. Find domain and range
b. Find slope and intercepts
c. Find average rate of change
d. Graph.
f(x)= 2x/3 +1
g(x) = -x/3 -1
h(x) = -3x/4 +5
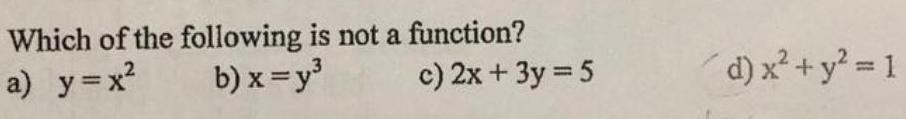
Math - Others
FunctionsWhich of the following is not a function?
a) y=x²
b)x=y³
c) 2x + 3y = 5
d) x² + y² = 1

Math - Others
FunctionsWhich of the following statements is/are true about the function
f(x) = - 5|x| +4x³.
f(x) is an odd function.
The graph of f(x) exhibits symmetry with respect to y axis.
The graph of f(x) exhibits symmetry with respect to origin.
f(x) is an even function.
None of the other statements are true because f(x) is neither even nor odd.
Math - Others
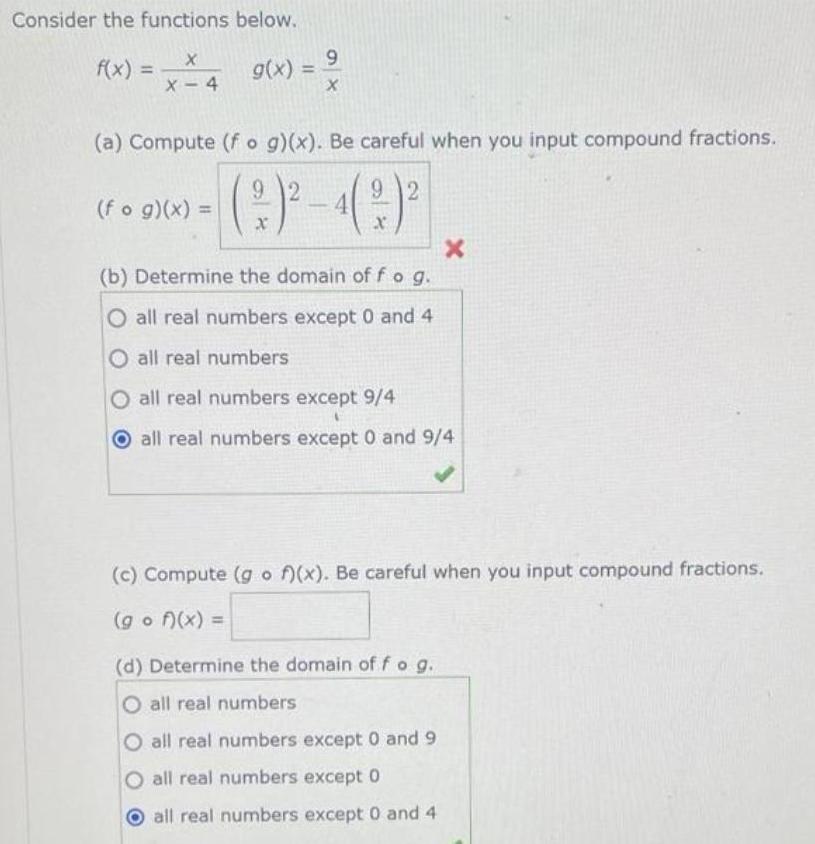
FunctionsConsider the functions below.
f(x) = x/(x-4)
g(x) = 9/x
(a) Compute (fog)(x). Be careful when you input compound fractions.
(fog)(x) =
(b) Determine the domain of f o g.
all real numbers except 0 and 4
all real numbers
all real numbers except 9/4
all real numbers except 0 and 9/4
(c) Compute (gof)(x). Be careful when you input compound fractions.
(gof)(x) =
(d) Determine the domain of f o g.
all real numbers
all real numbers except 0 and 9
all real numbers except 0
all real numbers except 0 and 4

Math - Others
Functions8. (Piecewise functions) Since each piece of a piecewise function is only graphed for part of the domain, we usually don't get the whole shape for each piece. Show what each shape looks like when it is cut off by the given domain. Make sure to determine if endpoints should be open circles or closed circles. The first and last are done for you as examples.
a) y = (x + 2)², if x < -2
b) y = x, if - 2 ≤ x < 2
c) y = √x-1, if x ≥ 2
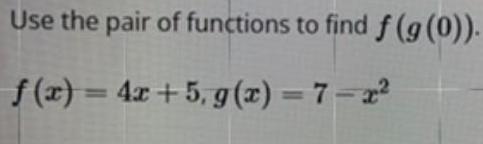
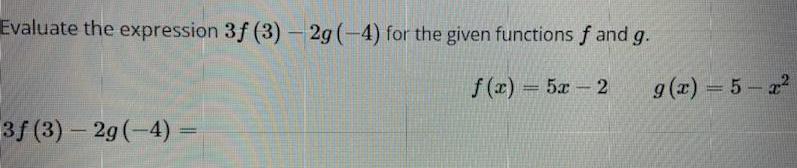
Math - Others
FunctionsEvaluate the expression 3f (3) - 2g (-4) for the given functions f and g.
f(x) = 5x - 2 g(x) = 5-x²
3f (3) - 2g (-4)=
Math - Others
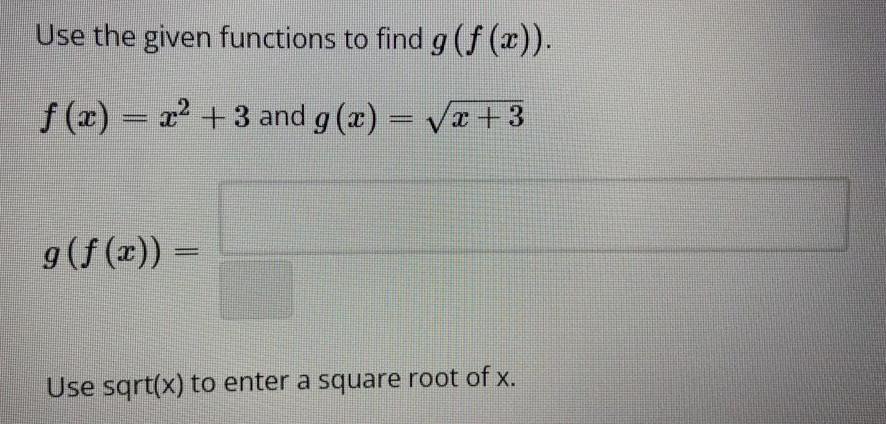
FunctionsUse the given functions to find g (f(x)).
f(x) = x² +3 and g(x) = √x +3
g (f(x)) =
Use sqrt(x) to enter a square root of x.
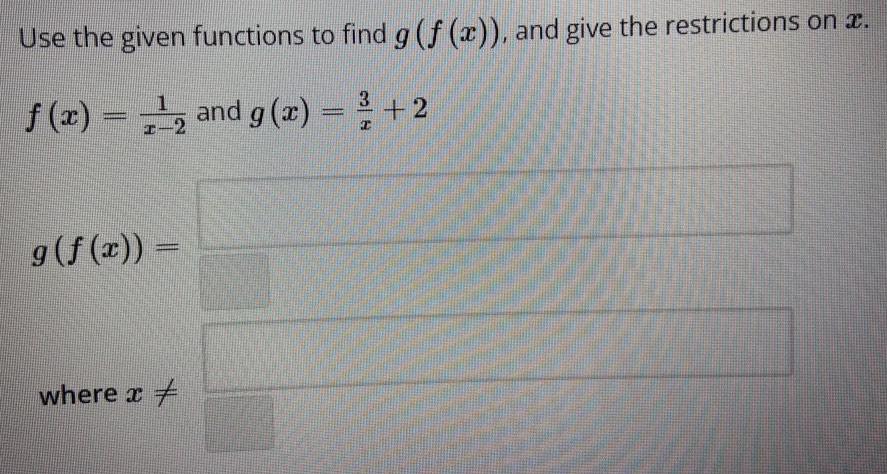
Math - Others
FunctionsUse the given functions to find g (f(x)), and give the restrictions on x
f(x)=1/x-2 and g(x)= 3/x +2
g (ƒ (x)) =
where x ≠
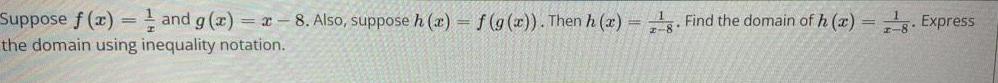
Math - Others
FunctionsSuppose f(x)=1/x and g(x)=x-8. Also, suppose h(x) = f(g(x)). Then h(x) = 1/x-8. Find the domain of h (x) =1/x-8 Express the domain using inequality notation.

Math - Others
FunctionsFind the domain of the function.
v(x)=√x-7
Write your answer using interval notation.
Math - Others
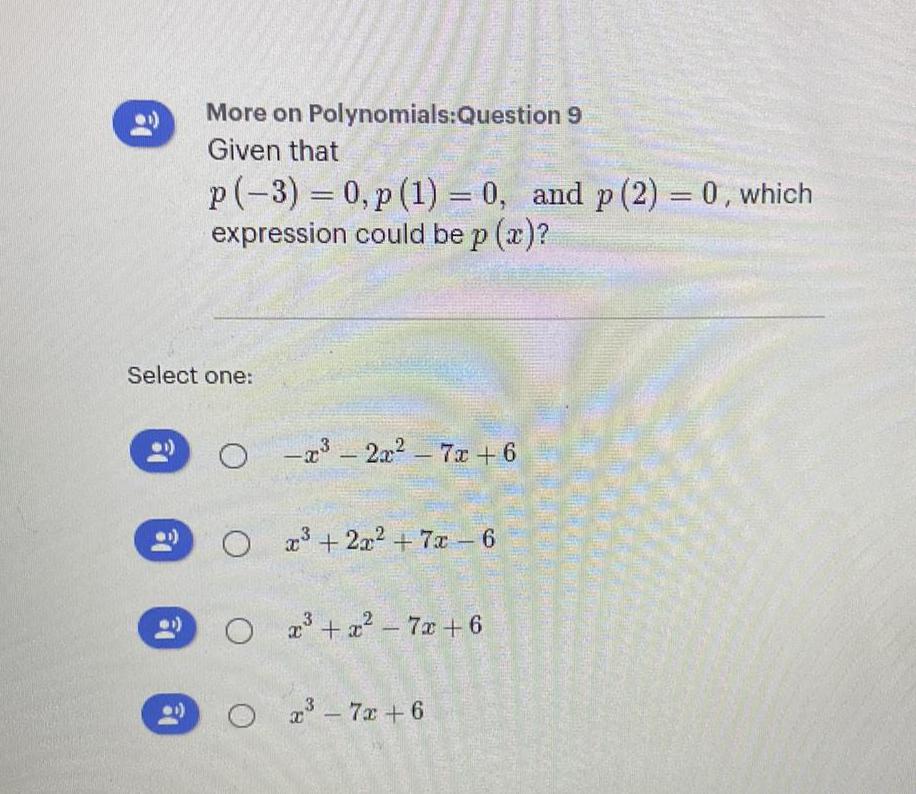
FunctionsMore on Polynomials:Question 9
Given that
p (-3) = 0, p (1) = 0, and p (2) = 0, which
expression could be p (x)?
-x³ - 2x² - 7x+6
x³ + 2x² + 7x-6
x³ + x² - 7x+6
x³-7x+6
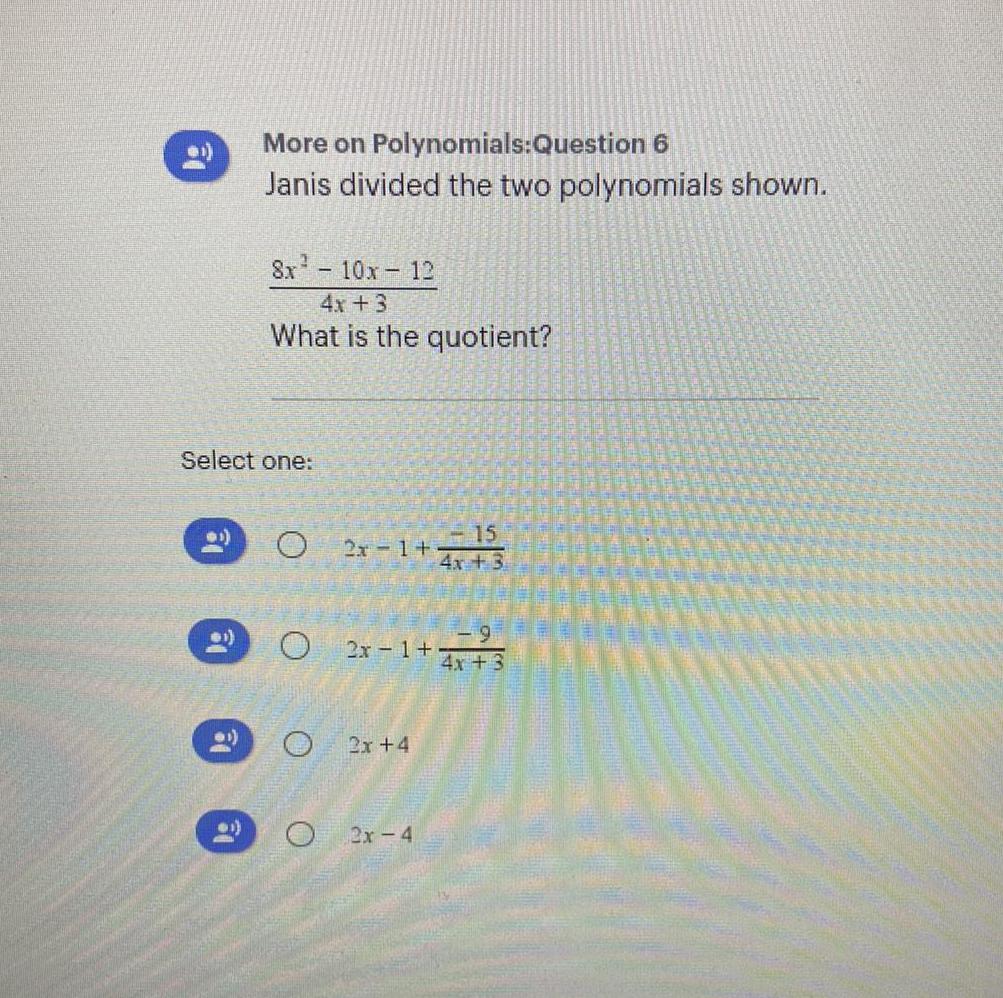
Math - Others
FunctionsJanis divided the two polynomials shown.
(8x² - 10x-129)/(4x + 3)
What is the quotient?
2x-1+(-15/(4x+3))
2x-1+(-9/(4x+3))
2x+4
2x-4
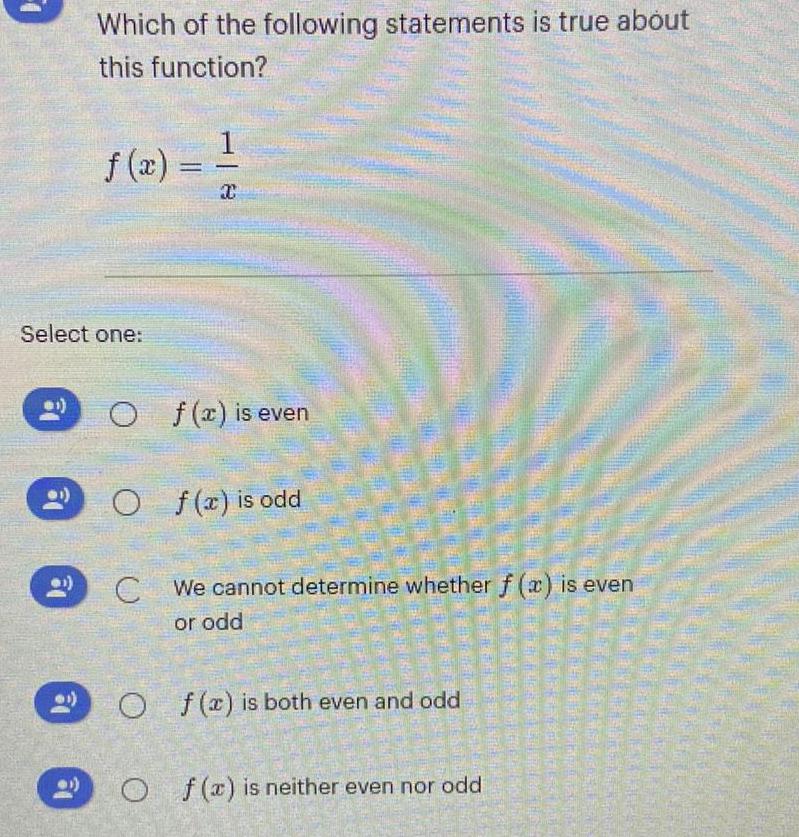
Math - Others
FunctionsWhich of the following statements is true about
this function?
Select one:
f(x) =1/x
f(x) is even
f(x) is odd
We cannot determine whether f(x) is even
or odd
f(x) is both even and odd
f(x) is neither even nor odd

Math - Others
Functionsuse the graphical method to locate the roots of f(x) = 5 cos(3x) - 2 sin(x) between x = 1 and x =6

Math - Others
FunctionsThe number of females in science continues to show steady increases. The number of female researchers in a certain country can be modeled by the function F(x) = 0.632x^1.566
where x is the number of years after 1940 and F(x) is the number of female researchers in thousands.
a. What type of function is this?
b. What is F(20)? What does it mean?
c. How many female researchers will there be in 2030?
a. F(x) = 0.632x^1.566 is a_________function.
Math - Others
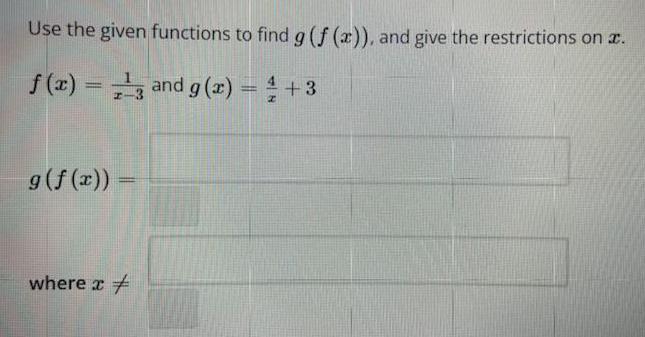
FunctionsUse the given functions to find g (f (x)), and give the restrictions on .
f(x) = 1/x-3and g(x) = 4/x +3
g (f(x))
where x ≠
Math - Others
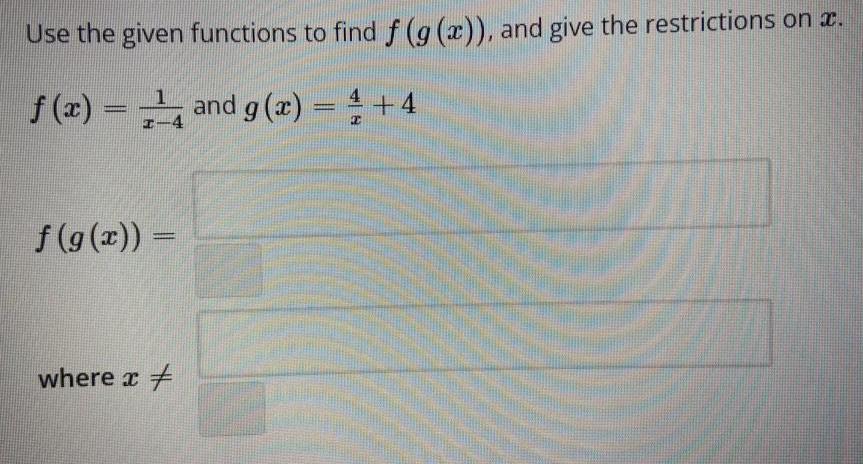
FunctionsUse the given functions to find f (g(x)), and give the restrictions on a.
f(x) = 1/x-4 and g(x) = 4/x + 4
f(g(x)) =
where x ≠



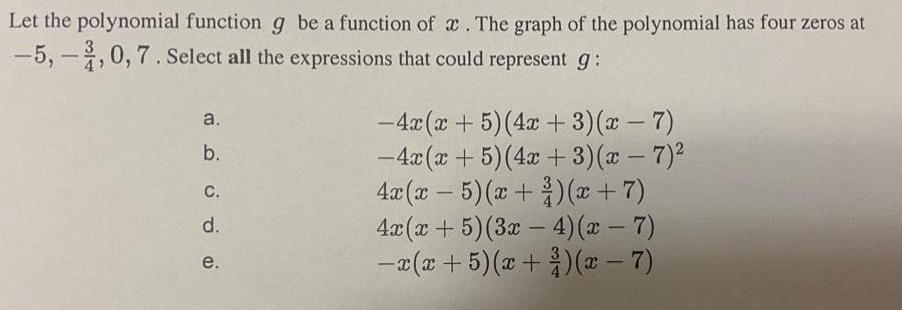
Math - Others
FunctionsLet the polynomial function g be a function of x. The graph of the polynomial has four zeros at
-5, -3/4,0, 7. Select all the expressions that could represent g:
a. -4x(x + 5) (4x + 3)(x-7)
b. -4x(x + 5) (4x+3)(x-7)²
c. 4x(x - 5)(x+3)(x+7)
d. 4x(x + 5) (3x - 4)(x-7)
e. -x(x + 5) (x+³)(x-7)

Math - Others
FunctionsFind the domain of f (x) = 2x − 1
O (-∞, 0) U (0, ∞)
0 (-∞, ∞)
0 (-∞, -¹) U ( 1/2, ∞)
0 (-∞,-1/2) U (-1/2,∞)
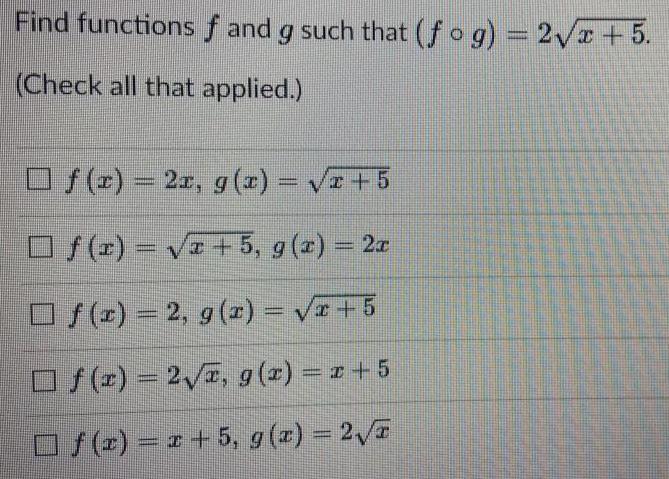
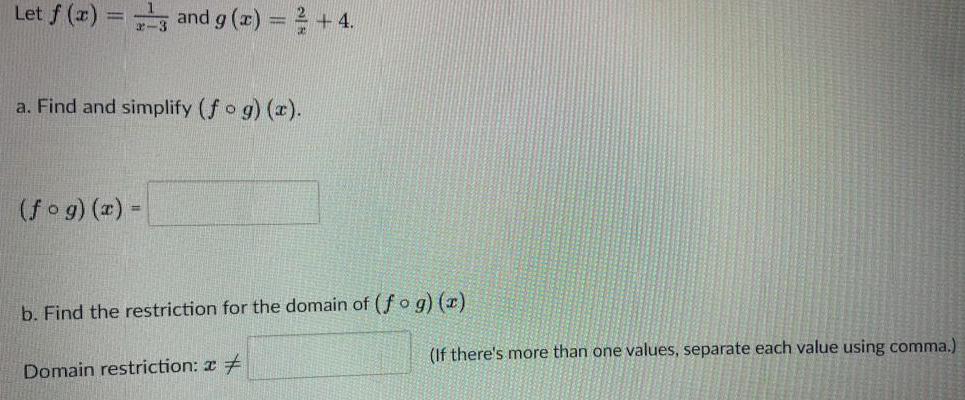
Math - Others
FunctionsLet f (x)
2-3
and g(x) = ² + 4.
a. Find and simplify (fog)(x).
(fog)(x) =
b. Find the restriction for the domain of (fog)(x)
Domain restriction:
(If there's more than one values, separate each value using comma.)

Math - Others
FunctionsDoes the relation represent y as a function of x?
2x=5y+3/(9y- 4)
No because there are values of x that correspond to more than one value of y.
Yes because each value of x corresponds to exactly one value of y.
Yes because the relation is described by an equation containing x and y.
No because the equation is not solved for y.
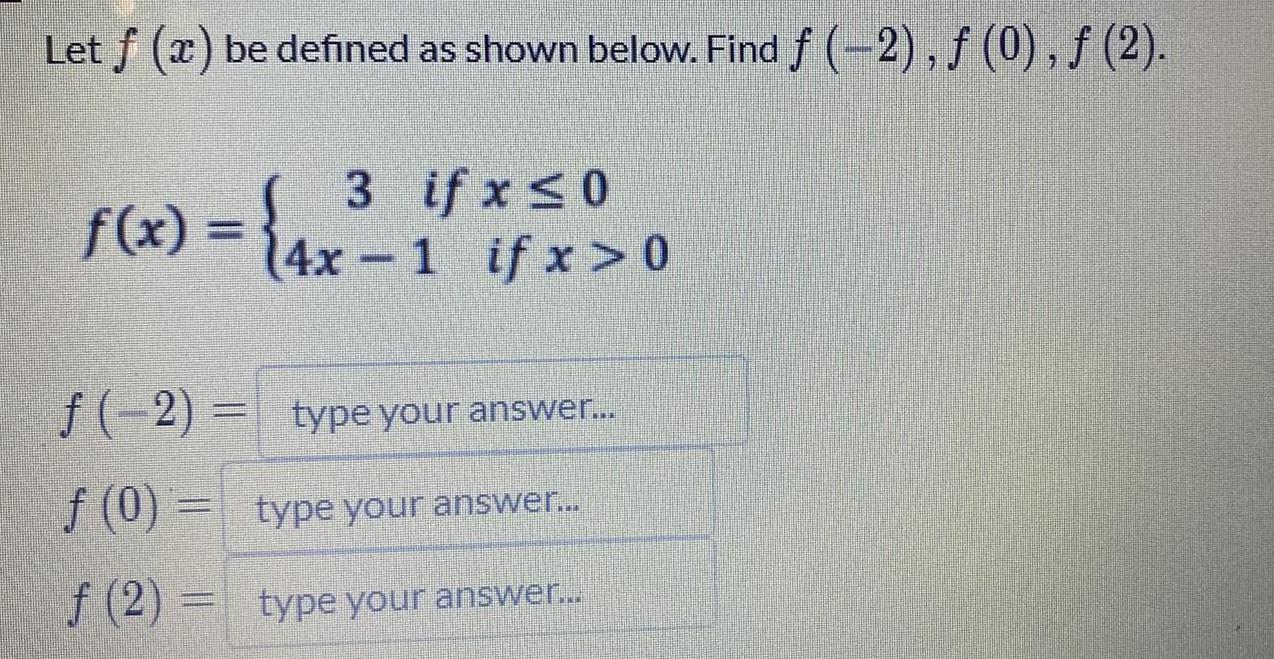
Math - Others
FunctionsLet f (x) be defined as shown below. Find ƒ (−2), ƒ (0), ƒ (2).
3 if x ≤0
f(x) = (4x-1 if x > 0
f(-2)=
f (0)
f(2)=
![Find the domain of f (x) = √4 – x.
(4,∞)
(4,∞)
(-∞,4]
(-∞,4)
[4, ∞)
(-∞, 4) U (4, ∞)
(-∞,∞)](https://media.kunduz.com/media/sug-question/raw/84230533-1657013046.3421237.jpeg?w=256)
Math - Others
FunctionsFind the domain of f (x) = √4 – x.
(4,∞)
(4,∞)
(-∞,4]
(-∞,4)
[4, ∞)
(-∞, 4) U (4, ∞)
(-∞,∞)
![Consider h(w) = (w +9) (w+4) (w + 1) on [-9, -1].
Determine the interval over which h is continuous and the interval over which h is differentiable.
h is continuous on_________
h is differentiable on___________](https://media.kunduz.com/media/sug-question/raw/84229582-1656998768.7695386.jpeg?w=256)
Math - Others
FunctionsConsider h(w) = (w +9) (w+4) (w + 1) on [-9, -1].
Determine the interval over which h is continuous and the interval over which h is differentiable.
h is continuous on_________
h is differentiable on___________
![Consider f(x) = 6 + (− 9x² - 18x) e^x on [ - 2, 0].
Determine the interval over which f is continuous and the interval over which f is differentiable.
f is continuous on__________
f is differentiable on_______](https://media.kunduz.com/media/sug-question/raw/84229588-1656998718.845937.jpeg?w=256)
Math - Others
FunctionsConsider f(x) = 6 + (− 9x² - 18x) e^x on [ - 2, 0].
Determine the interval over which f is continuous and the interval over which f is differentiable.
f is continuous on__________
f is differentiable on_______
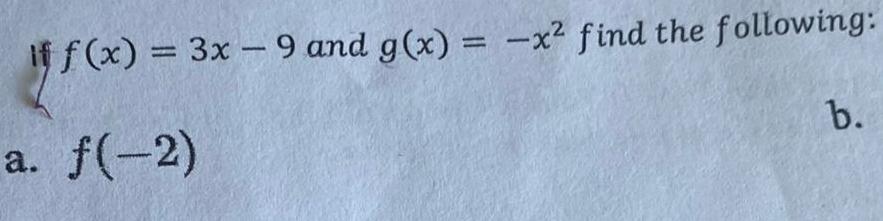
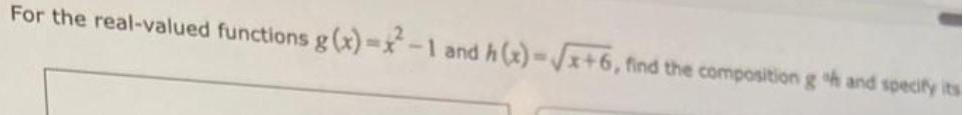
Math - Others
FunctionsFor the real-valued functions g(x)=x²-1 and h(x)=√x+6, find the composition go and specify its domain.

Math - Others
FunctionsLet f(x) = 3x - 1 and g(x) = 2x². Perform the function operation and then find the domain of the result.
(f+g)(x)

Math - Others
Functions5. Find the inverse of each function. Is the inverse a function?
a. f(x) = x³
b. f(x) = √2x-1 +3

Math - Others
FunctionsLet f(x) = x - 1 and g(x) = x². Perform the function operation and then find the domain of the result.
(f - g)(x)

Math - Others
FunctionsFind the parent function for each graph below. Then describe the transformations that occurred to get each function below.
a. y = -√16x + 32
b. y =3√8x - 24 + 1