Functions Questions and Answers
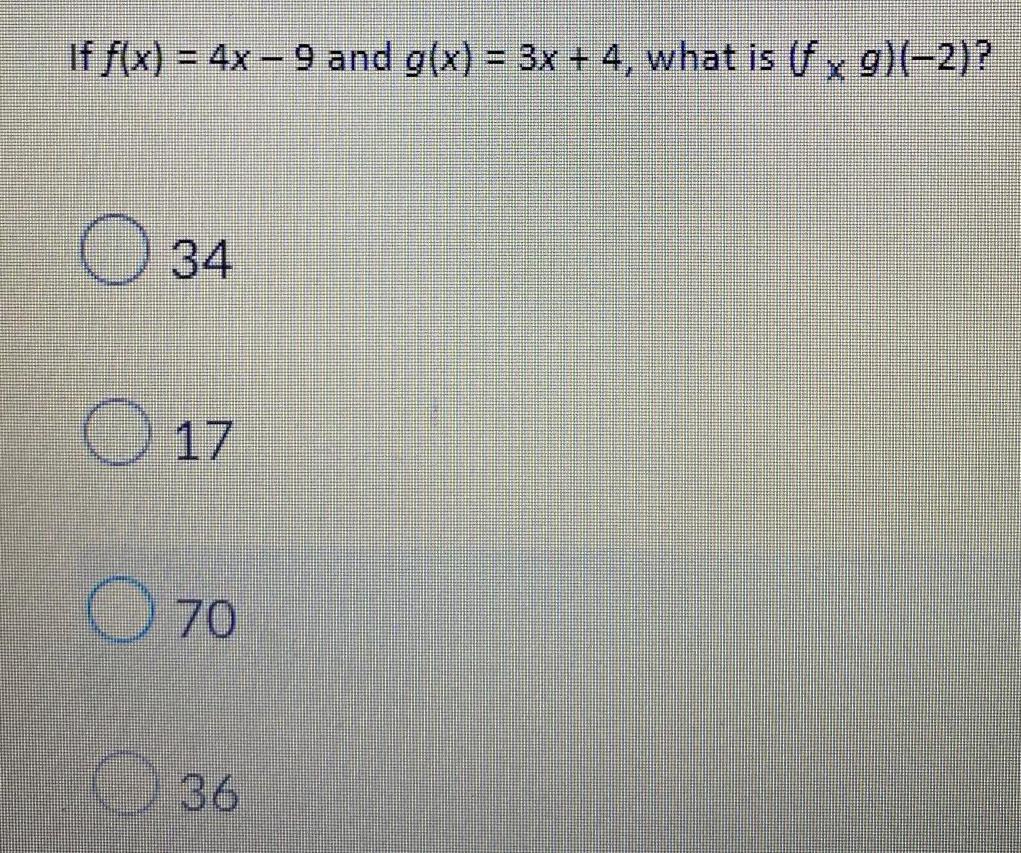

Math - Others
FunctionsIf f(x) = log₂ x and g(x) = 2^x, what is (g — f) (8) ?
Round your answer to two decimal places if needed. Upload a picture of your work
Your Answer:
Math - Others
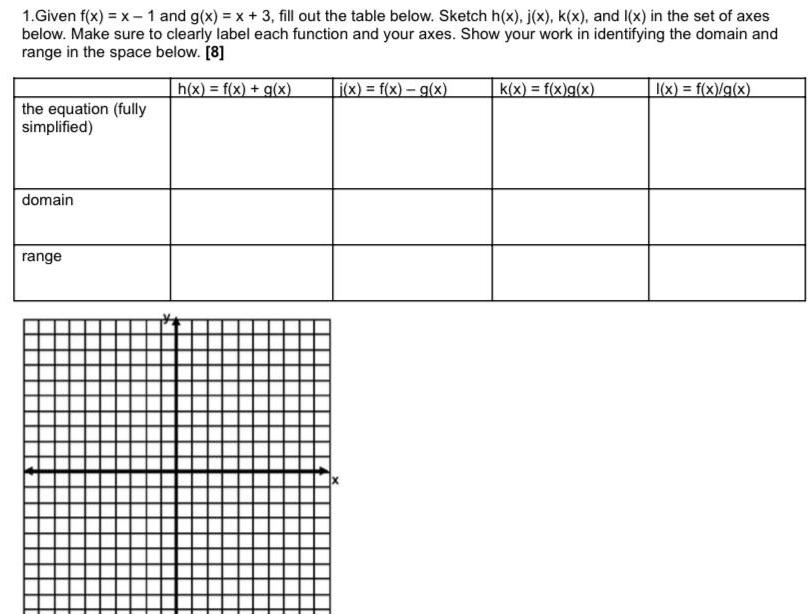
Functions1.Given f(x) = x - 1 and g(x) = x + 3, fill out the table below. Sketch h(x), j(x), k(x), and 1(x) in the set of axes below. Make sure to clearly label each function and your axes. Show your work in identifying the domain and range in the space below.
the equation (fully simplified)
domain
range
h(x) = f(x) + g(x)
i(x) = f(x) = g(x)
k(x) = f(x)g(x)
1(x) = f(x)/g(x)

Math - Others
Functions1. As a tornado moves, its speed increases. The function S(d) = 93logd + 65 relates the speed of the wind, S, in miles per hour, near the centre of a tornado to the distance that the tornado has travelled, d, in miles.
(a) Calculate the average rate of change for the speed of the wind at the centre of a tornado from:
(i) mile 10 to 100
(ii) mile 100 to 1000
(iii) Describe how the two rates above compare with respect to the given information.
(b) Estimate the instantaneous rate of change at d = 1000 miles. Use an interval of 0.01. Round your answer to the nearest hundredth. Do not find the instantaneous rate of change using the difference quotient or any Calculus method. Explain what the value represents in this situation.


Math - Others
FunctionsThe function f(x) =8x/x+3 is one-to-one. Find its inverse and check your answer.
![The domain of f(t) is [-10,10], and its range is [-3,2]. What are the domain and
range of
a. f(2t)
b. f(t/2)
c. 0.2f(t) +3
d. 0.2f(-2t+2)+3](https://media.kunduz.com/media/sug-question/raw/84622779-1658601576.9974697.jpeg?w=256)
Math - Others
FunctionsThe domain of f(t) is [-10,10], and its range is [-3,2]. What are the domain and
range of
a. f(2t)
b. f(t/2)
c. 0.2f(t) +3
d. 0.2f(-2t+2)+3
Math - Others
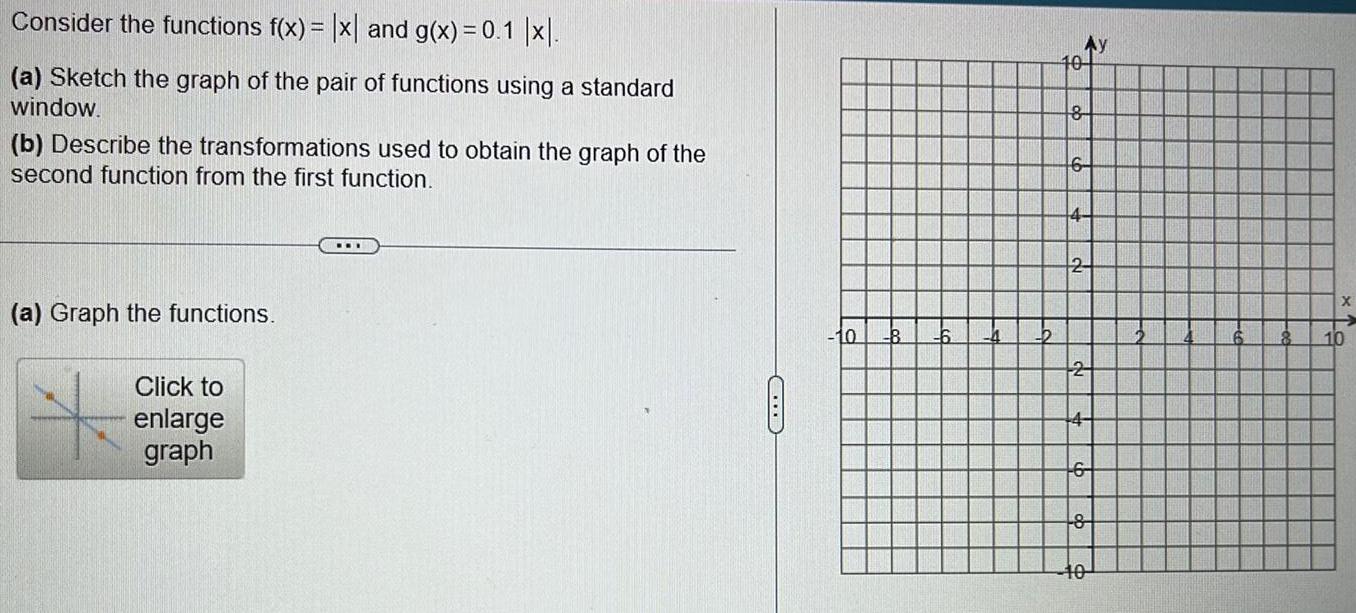
FunctionsConsider the functions f(x) = |x| and g(x) = 0.1 |x|.
(a) Sketch the graph of the pair of functions using a standard window.
(b) Describe the transformations used to obtain the graph of the second function from the first function.
(a) Graph the functions.
Math - Others
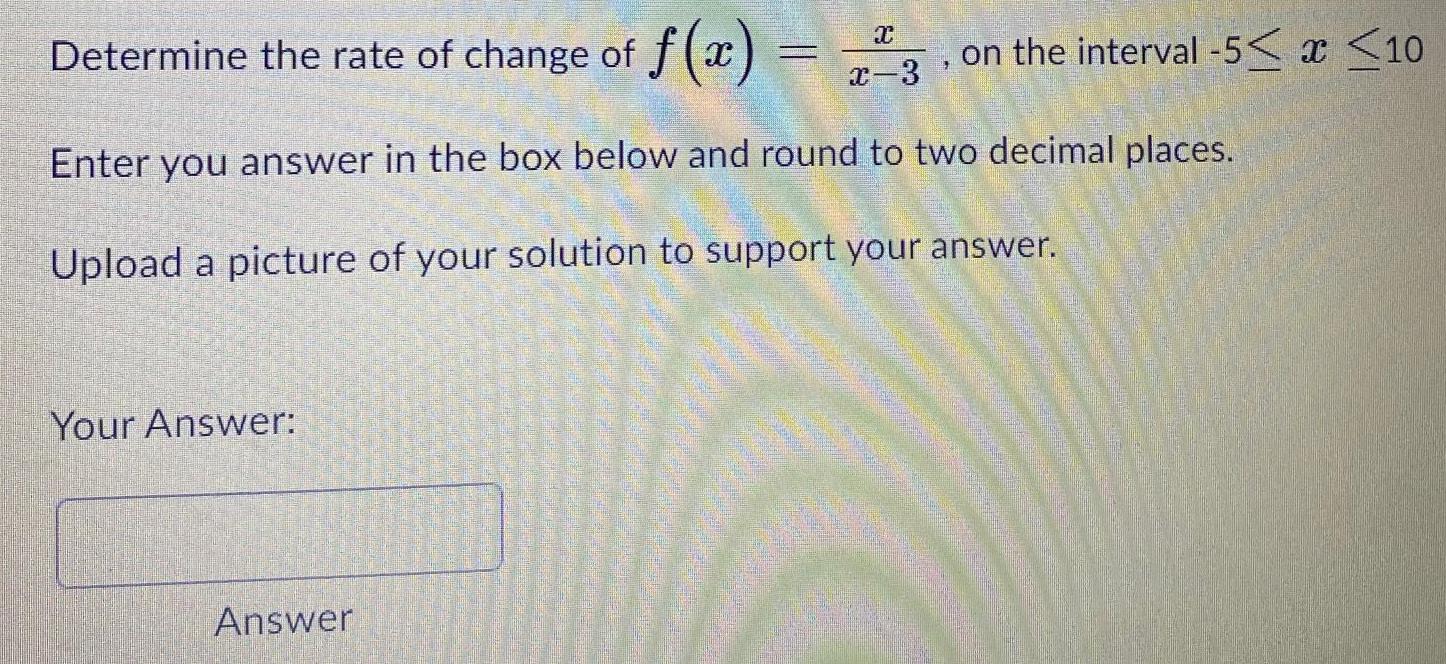
FunctionsDetermine the rate of change of f(x) = x/x-3 on the interval -5≤ x ≤10
Enter you answer in the box below and round to two decimal places.
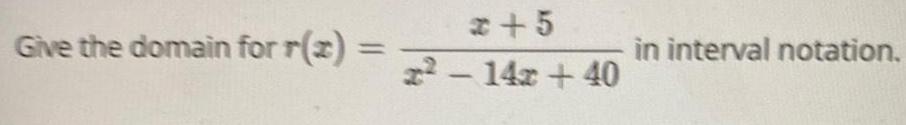
Math - Others
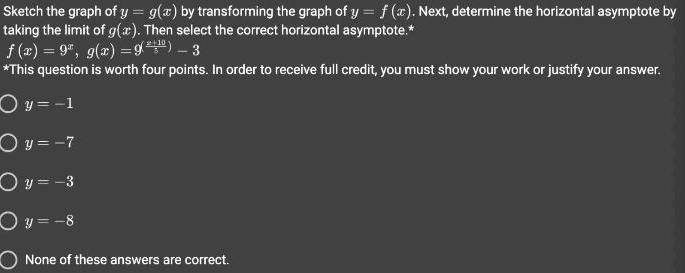
FunctionsSketch the graph of y = g(x) by transforming the graph of y = f(x). Next, determine the horizontal asymptote by taking the limit of g(x). Then select the correct horizontal asymptote.*
f(x) = 9^x , g(x) = 9(x+10/5) - 3
*This question is worth four points. In order to receive full credit, you must show your work or justify your answer.
y=-1
y=-7
y=-3
y = -8
None of these answers are correct.

Math - Others
FunctionsGive the domain of each of the following functions in interval notation.
g(x) = -7 /25-x²
p(x) = -3/49 + x²

Math - Others
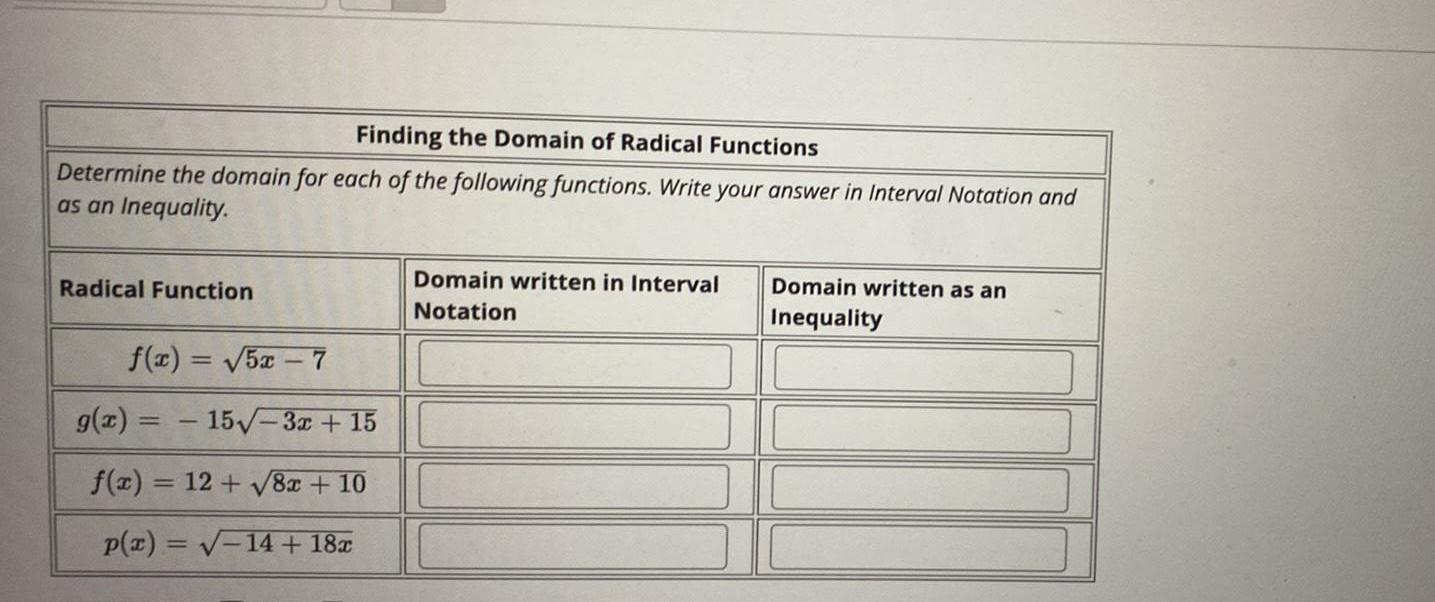
FunctionsFinding the Domain of Radical Functions
Determine the domain for each of the following functions. Write your answer in Interval Notation and as an Inequality.
Radical Function Domain written in Interval Domain written as
Notation an Inequality
f(x) = √5x - 7
g(x) = -15√-3x + 15
f(x) = 12 + √8x + 10
p(x) = √-14+ 18x
Math - Others
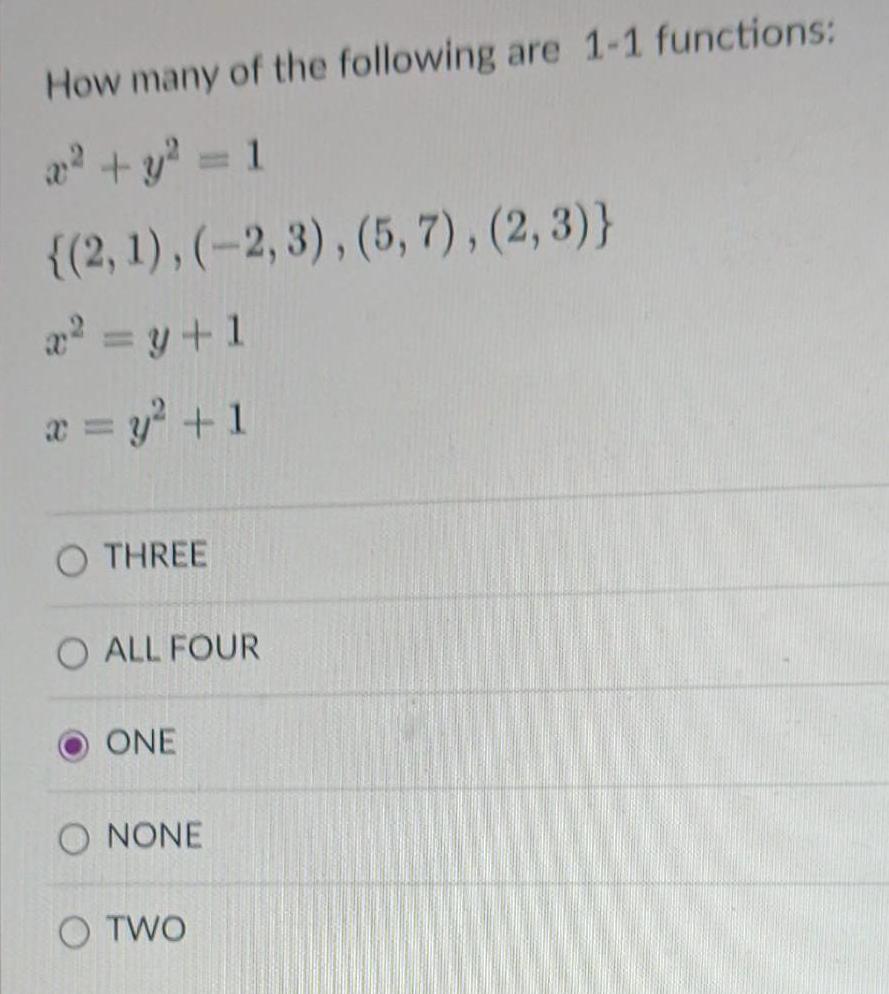
FunctionsHow many of the following are 1-1 functions:
x² + y² = 1
{(2, 1), (-2,3), (5,7), (2,3)}
x² = y + 1
x = y² + 1
THREE
ALL FOUR
ONE
NONE
TWO


Math - Others
FunctionsIf f(x) = 6x-9 and g(x)=x+9/6
(a) f(g(x)) =
(b) g(f(x)) =
(c) Thus g(x) is called an_____function of f(x)
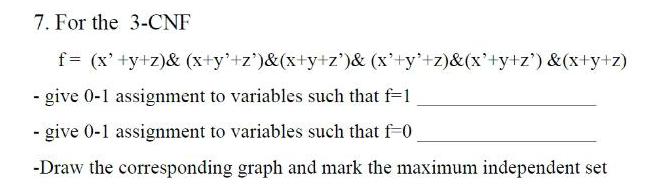
Math - Others
FunctionsFor the 3-CNF
f = (x' +y+z)& (x+y+z')&(x+y+z')& (x+y+z)&(x+y+z') &(x+y+z)
- give 0-1 assignment to variables such that f=1
- give 0-1 assignment to variables such that f=0
-Draw the corresponding graph and mark the maximum independent set

Math - Others
FunctionsThe function h is defined below.
h(x)= x²-x-30/x^2-11x+24
Find all values of x that are NOT in the domain of h.
If there is more than one value, separate them with commas.
Math - Others
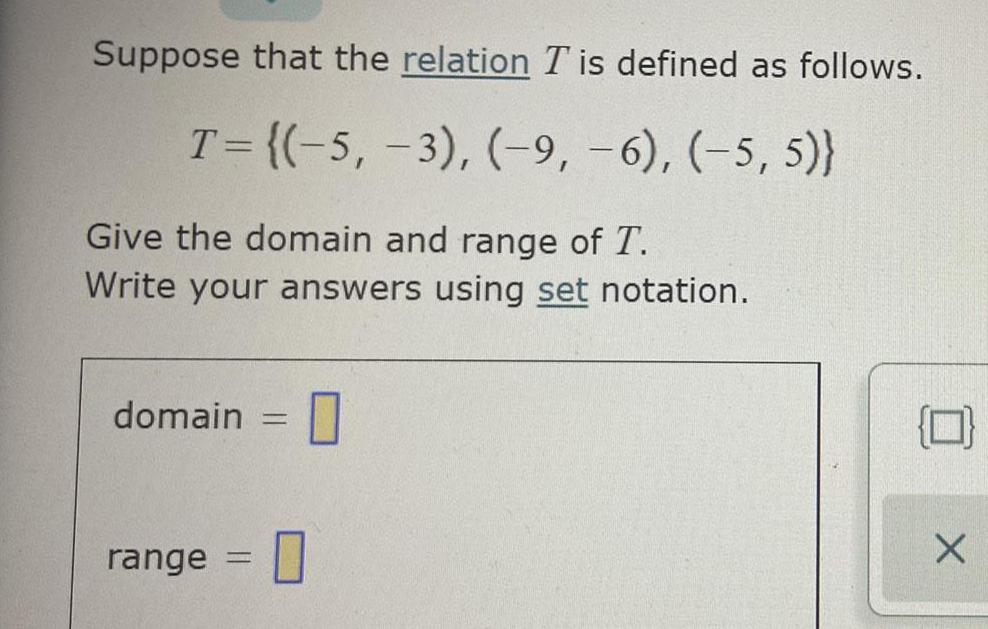
FunctionsSuppose that the relation T is defined as follows.
T= {(-5, -3), (-9, -6), (-5,5)}
Give the domain and range of T.
Write your answers using set notation.
domain
range
Math - Others
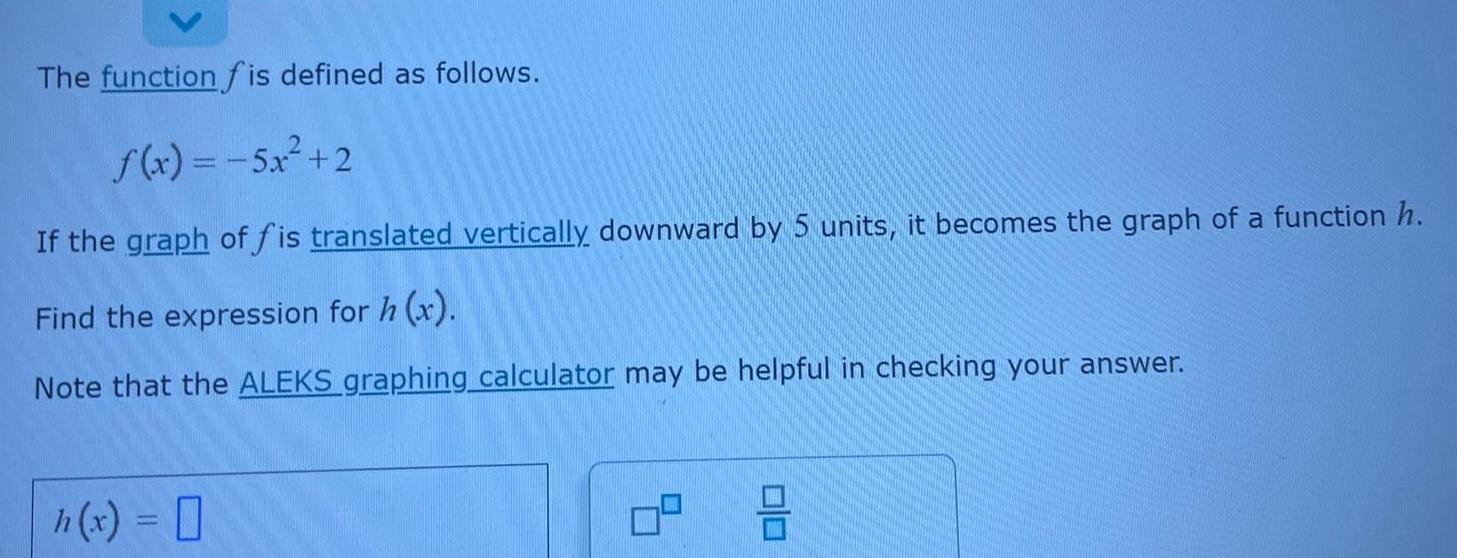
FunctionsThe function f is defined as follows.
f(x) = -5x²+2
If the graph of fis translated vertically downward by 5 units, it becomes the graph of a function h.
Find the expression for h (x).
Note that the ALEKS graphing_calculator may be helpful in checking your answer.
h(x) =
Math - Others
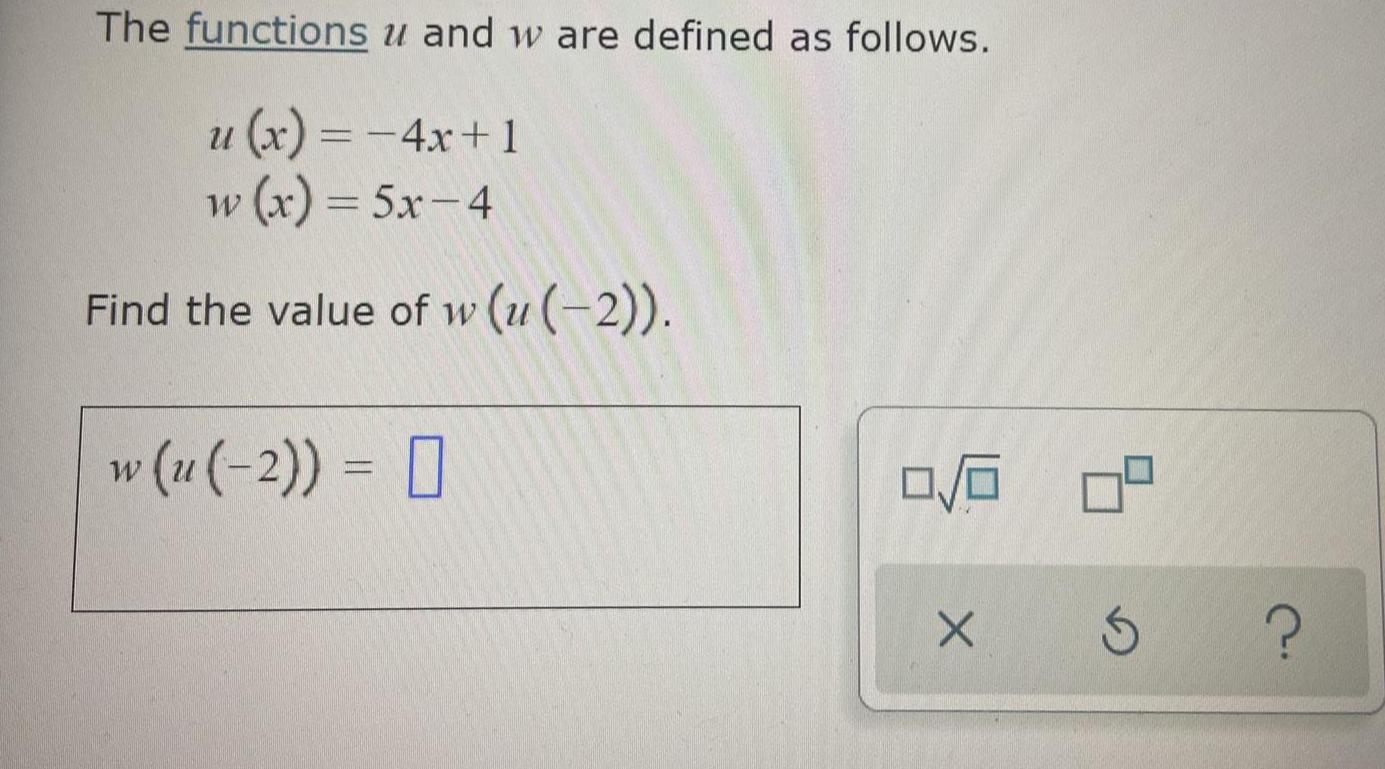
FunctionsThe functions u and w are defined as follows.
u(x) = -4x+1
w (x) = 5x-4
Find the value of w (u (-2)).
w (u(-2)) =
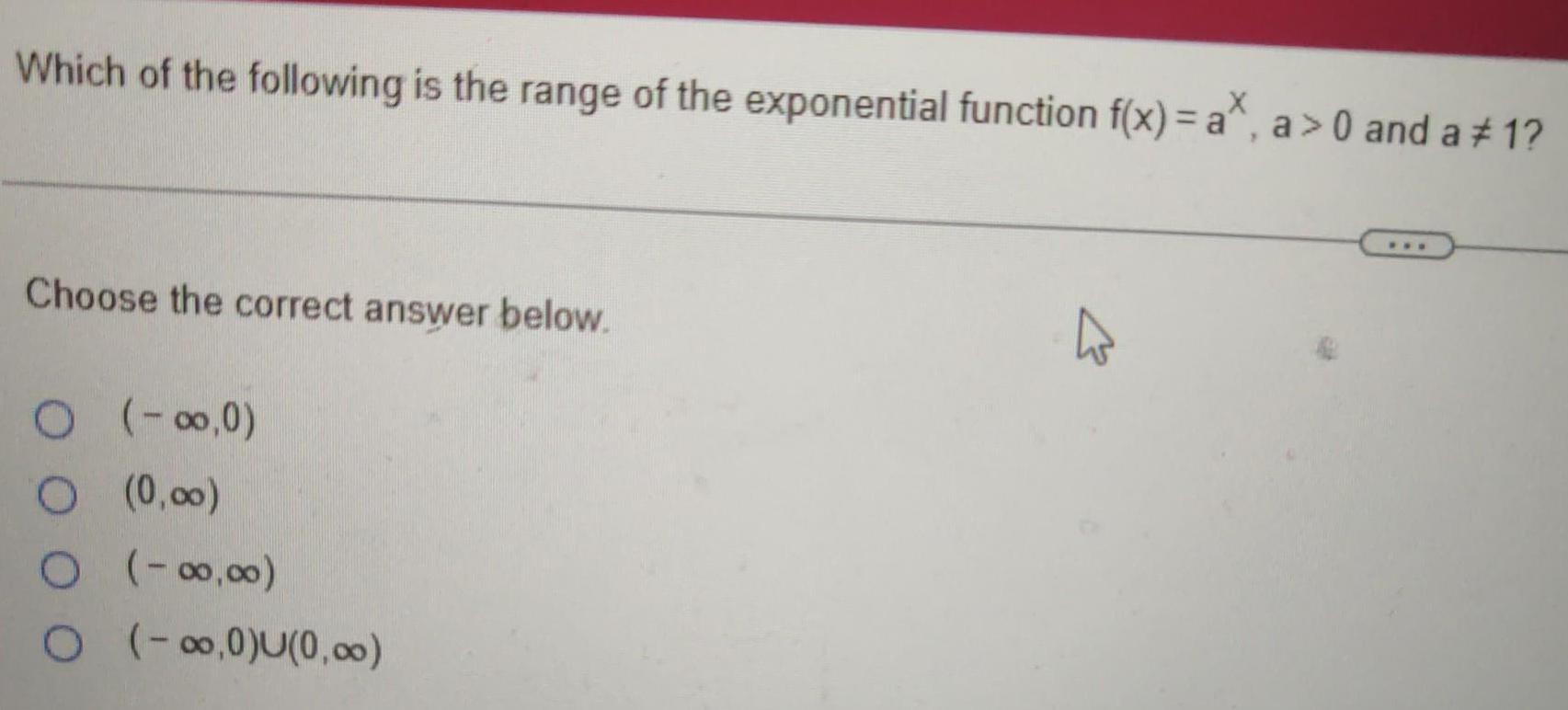
Math - Others
FunctionsWhich of the following is the range of the exponential function f(x) = a^x, a>0 and a ≠1?
Choose the correct answer below.
(-∞,∞)
(0,∞)
(-∞,∞)
(-∞,0)U(0,∞)

Math - Others
FunctionsGiven the function f(x)=-5-2/3x
(a) Slope:
(b) y-intercept:
(c) Is this function increasing, decreasing or constant?
(d) Solve the inequality: f(x)≥ -1
Use interval notation. Use Int for positive infinity and in for negative infinity. Use for union. Don't include any spaces in your solution.
(e) Average rate of change

Math - Others
Functions2. Make a table for r = 2 cos(30) with 0=15° +30°k with k going from 0 to 11 along with = 90°k with k going from 0 to 4 and plot these points (by hand). Use these points to help you sketch a graph of r = 3 sin(20).

Math - Others
FunctionsLet f (x) = 4^-x-1. Find the domain and range of f (x).
Domain: (-∞, ∞)
Range: (-∞, -1)
Domain: (-∞, ∞)
Range: (0, ∞)
O Domain: (-∞, ∞)
Range: (-1, ∞)
Domain: (-∞, ∞)
Range: (-∞0,0)
Domain: (-1, ∞)
Range: (-∞, ∞)
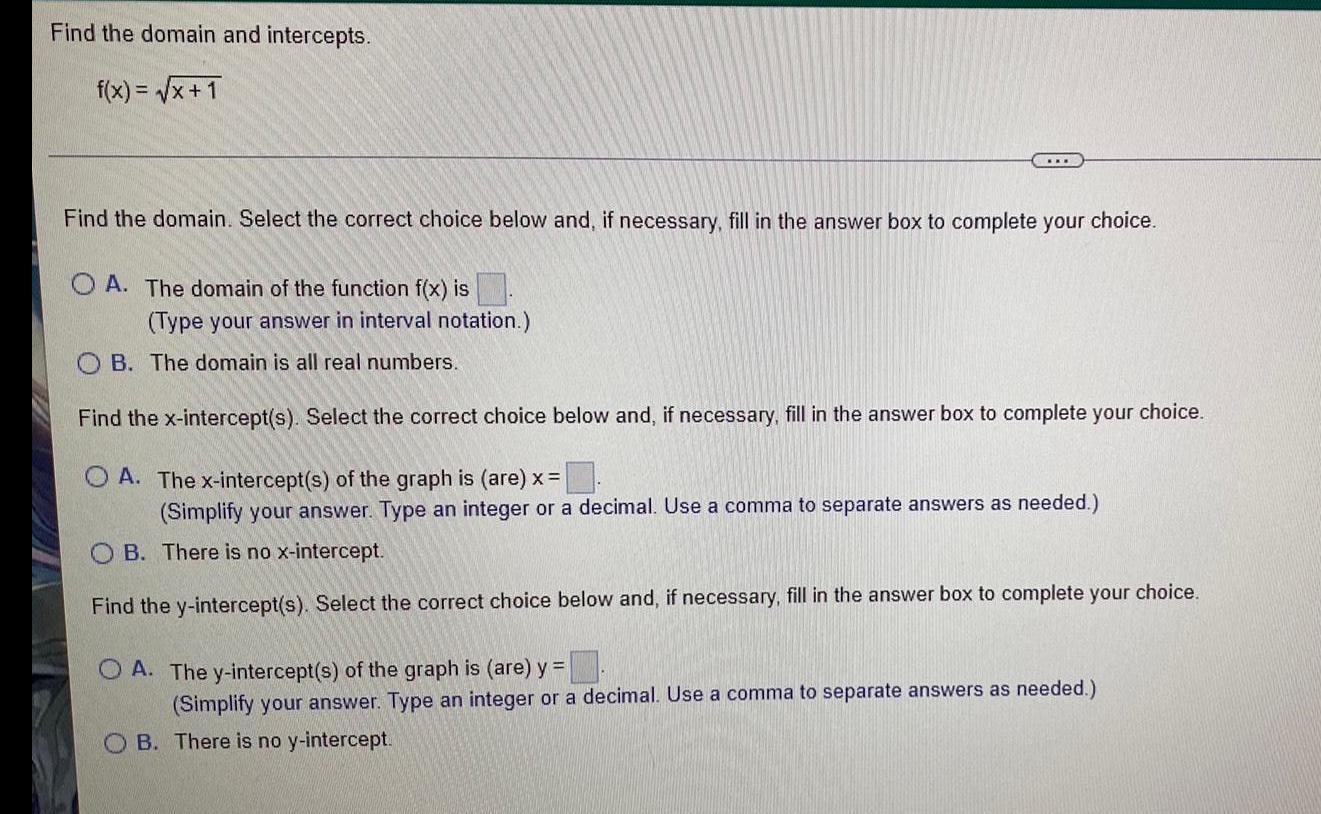
Math - Others
FunctionsFind the domain and intercepts.
f(x)=√x+1
Find the domain. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The domain of the function f(x) is
(Type your answer in interval notation.)
B. The domain is all real numbers.
Find the x-intercept(s). Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The x-intercept(s) of the graph is (are) x =
(Simplify your answer. Type an integer or a decimal. Use a comma to separate answers as needed.)
B. There is no x-intercept.
Find the y-intercept(s). Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The y-intercept(s) of the graph is (are) y =
(Simplify your answer. Type an integer or a decimal. Use a comma to separate answers as needed.)
B. There is no y-intercept.

Math - Others
FunctionsA set of exam scores is normally distributed with a mean = 80 and standard deviation = 9.
Use the Empirical Rule to complete the statements below.
95% of the data values lie between ___and___
___% of the exam scores are between 71 and 80.
___% of the exam scores are between 80 and 98.
___% of the exam scores are between 89 and 98.
___% of the exam scores are greater than or equal to 71.

Math - Others
FunctionsThe parabola y = x² is compressed vertically by a factor of 0.3, translated up 1 unit and to the right 3 units.
Write the equation of the new parabola in the form y = a(x - h)² + k.

Math - Others
FunctionsThe function y = sin x has been transformed. It now has amplitude of 7.8, a period of 22, a phase shift of 10 units to the right, a vertical translation of 4.5 units down, and is reflected over the x-axis. Given that (π/6, 1/2) is a point in the parent function, use mapping notation to determine the x-coordinate of its image point in the transformed function.
Enter the numerical value of the x-coordinate only in the box below rounded to two decimals.
Upload a picture of your work.


Math - Others
FunctionsRewrite the equation of the circle (x-2)^2 + y^2 =3 in general form.
x²+y²-4x+1=0
x²+y²-4x+7=0
x²+y²-2x+1=0
x²+y²-2x+7=0

Math - Others
FunctionsI understand that I have to derive both sides however I don't understand how the integral on the right side of the equation turns into a negative (-xf(x))

Math - Others
FunctionsHow is the graph of log (x + 3) - 4 translated from the graph of log x?
shifted right 4 units and down 3 units
shifted right 3 units and up 4 units
shifted left 4 units and up 3 units
shifted left 3 units and down 4 units
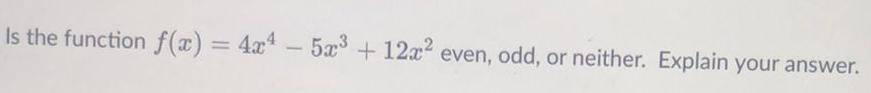
Math - Others
FunctionsIs the function f(x) = 4x^4 - 5x³ + 12x² even, odd, or neither. Explain your answer.

Math - Others
FunctionsHow is the graph of y = 9(3)x+² + 6 translated from the graph of y = 9(3)x?
6 units right and 2 units down
2 units right and 6 units up
6 units left and 2 units down
2 units left and 6 units up

Math - Others
FunctionsWhich of the following describes the graph of f-¹(x)?
The graph of f-1(x) is the reflection of the graph of f(x) in the y-axis.
The graph of f-¹(x) is the reflection of the graph of f(x) in the x-axis.
The graph of f-1(x) is the reflection of the graph of f(x) in the line y = x.
The graph of f-1(x) is the reflection of the graph of f(x) in the line y = -x.

Math - Others
Functions13. Graph the rational function y=x/2x+2.Which quadrant does neither branch of the rational function pass through?
Quadrant 3
Quadrant 1
Quadrant 2
Quadrant 4

Math - Others
Functions8. Find the y-axis intercepts for the function f(x)=1/x
does not exist
(1,1)
(0,0)
(0, 1)

Math - Others
Functions14. For the function f(x) = 4x-3, evaluate and simplify the expression: f(a+h)-f(a)/h
f(a+h)-f(a)/h =4
ƒ(a+h)-f(a)/h = 4a+4h+3
f(a+h)-f(a)/h= 4a+4h-3
f(a+h)-f(a)/h= 4h

Math - Others
Functions15. Evaluate the function f(x) = -x²-1 and simplify at the indicated value: f(-a) = ?
f(-a)=-a²
f(-a)= a(a + 1)
f(-a)= -a²-a
f(-a)=-a²-1

Math - Others
FunctionsWhat is the multiple zero and multiplicity of f(x) = (x + 8)(x + 8)(x − 3)(x + 8)?
multiple zero = 3; multiplicity = -8
multiple zero = 3; multiplicity = 8
multiple zero = 8; multiplicity = 3
multiple zero = -8; multiplicity = 3

Math - Others
FunctionsSolve the equation in the real number system: (x^5) - 4(x^4) +4(x^3)+2x² -5x+2=0.
x = -1,1,2
x = -2,-1,1
x = -5,-4,1,2,4
x=-5,-4,1,2

Math - Others
FunctionsState the various transformations applied to the base function f(x) = (x^2) to obtain a graph of the function (x) = -2[(x - 1)² +31
A reflection about the y-axis, a vertical stretch by a factor of 2, a horizontal shift of 2 units to the right, and a vertical shift downward of 6 units.
A reflection about the x-axis, a vertical stretch by a factor of 2, a horizontal shift of 2 units to the right, and a vertical shift downward of 6 units.
A reflection about the y-axis, a vertical stretch by a factor of 2, a horizontal shift of 1 unit to the right, and a vertical shift downward of 6 units.
A reflection about the x-axis, a vertical stretch by a factor of 2, a horizontal shift of 1 unit to the right, and a vertical shift downward of 6 units.
![28. State the various transformations applied to the base function f(x) = x² to obtain a graph of the function g(x) = -2[(x - 1)² +3].
A reflection about the y-axis, a vertical stretch by a factor of 2, a horizontal shift of 2 units to the right, and a vertical shift downward of 6 units.
A reflection about the x-axis, a vertical stretch by a factor of 2, a horizontal shift of 2 units to the right, and a vertical shift downward of 6 units.
A reflection about the y-axis, a vertical stretch by a factor of 2, a horizontal shift of 1 unit to the right, and a vertical shift downward of 6 units.
A reflection about the x-axis, a vertical stretch by a factor of 2, a horizontal shift of 1 unit to the right, and a vertical shift downward of 6 units.](https://media.kunduz.com/media/sug-question/raw/84525723-1658073247.133293.jpeg?w=256)
Math - Others
Functions28. State the various transformations applied to the base function f(x) = x² to obtain a graph of the function g(x) = -2[(x - 1)² +3].
A reflection about the y-axis, a vertical stretch by a factor of 2, a horizontal shift of 2 units to the right, and a vertical shift downward of 6 units.
A reflection about the x-axis, a vertical stretch by a factor of 2, a horizontal shift of 2 units to the right, and a vertical shift downward of 6 units.
A reflection about the y-axis, a vertical stretch by a factor of 2, a horizontal shift of 1 unit to the right, and a vertical shift downward of 6 units.
A reflection about the x-axis, a vertical stretch by a factor of 2, a horizontal shift of 1 unit to the right, and a vertical shift downward of 6 units.

Math - Others
FunctionsIn this module assignment, many of your answers will involve monetary values, that is, dollars and cents. In WeBWork, you must remember to begin any monetary value with a dollar sign ($) and always round to the nearest penny, unless the instructions on a particular problem call for something else.
Practice by inputting the value $10,314.76 in the blank below. (You'll get credit for one homework question for doing so!) Note that you can either include the comma separator for the thousands place or not, WeBWork will accept either notation.
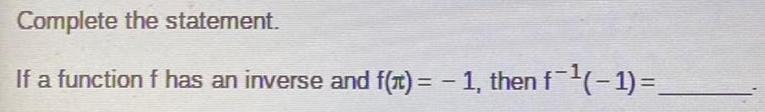
Math - Others
FunctionsComplete the statement.
If a function f has an inverse and f(π) = -1, then f¯¹(− 1) =_
Math - Others
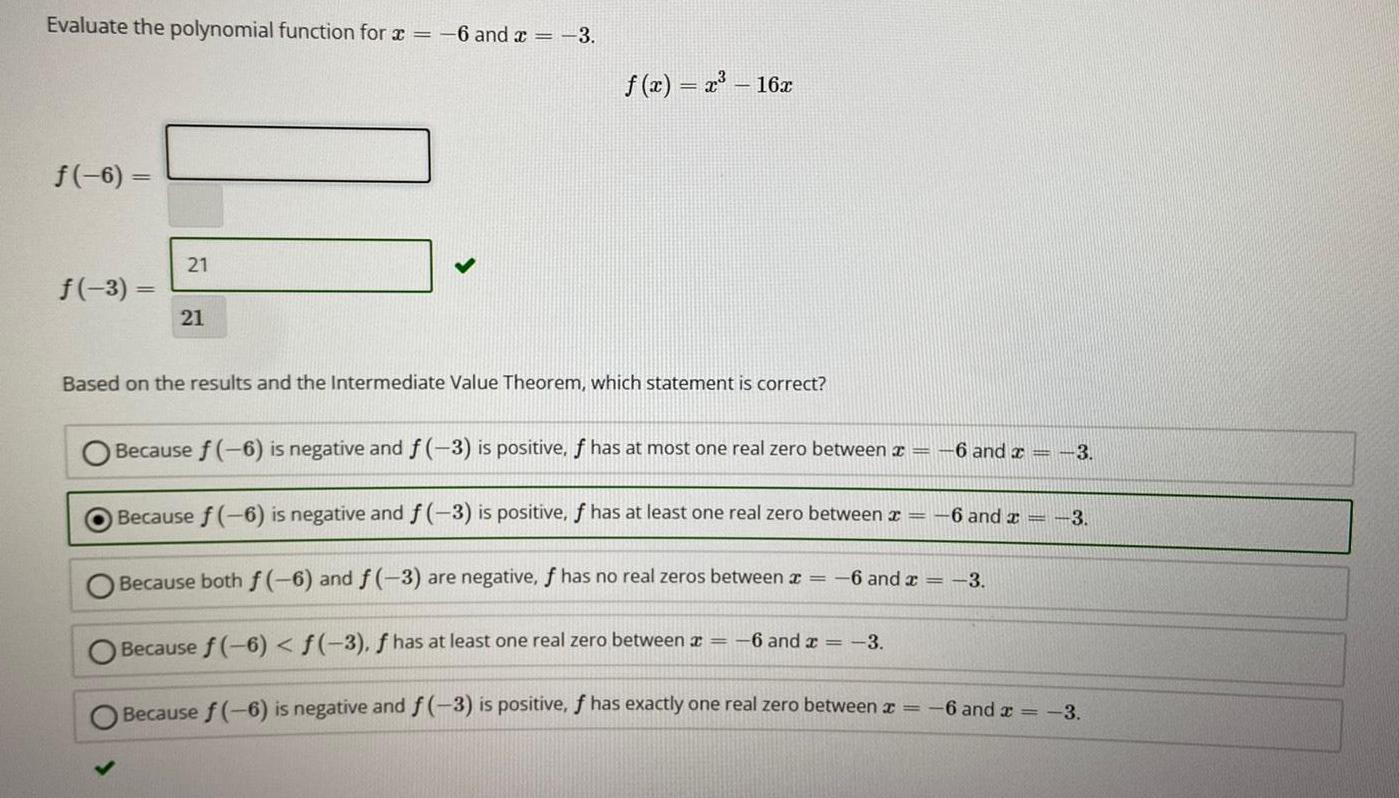
FunctionsEvaluate the polynomial function for x = -6 and x = -3.
f(x) = x³ - 16x
f(-6)=
f(-3) =
Based on the results and the Intermediate Value Theorem, which statement is correct?
Because f(-6) is negative and f(-3) is positive, f has at most one real zero between x= -6 and x= -3
Because f(-6) is negative and f(-3) is positive, f has at least one real zero between x = -6 and x= -3
Because both f(-6) and f(-3) are negative, f has no real zeros between x = -6 and x = -3
Because f(-6) < f(-3), f has at least one real zero between x = -6 and x = -3.
Because f(-6) is negative and f(-3) is positive, f has exactly one real zero between x = -6 and x = -3.
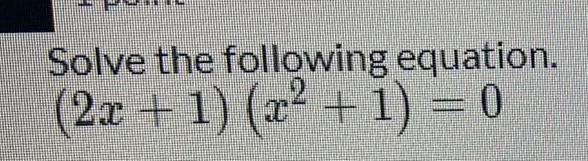
Math - Others
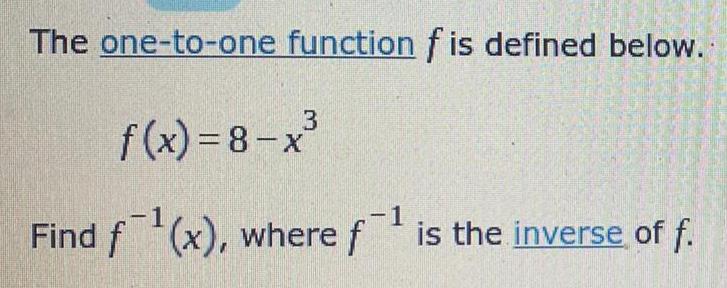
FunctionsThe one-to-one function f is defined below.
f(x)=8-x³
Find f⁻¹(x), where f⁻¹ is the inverse of f.