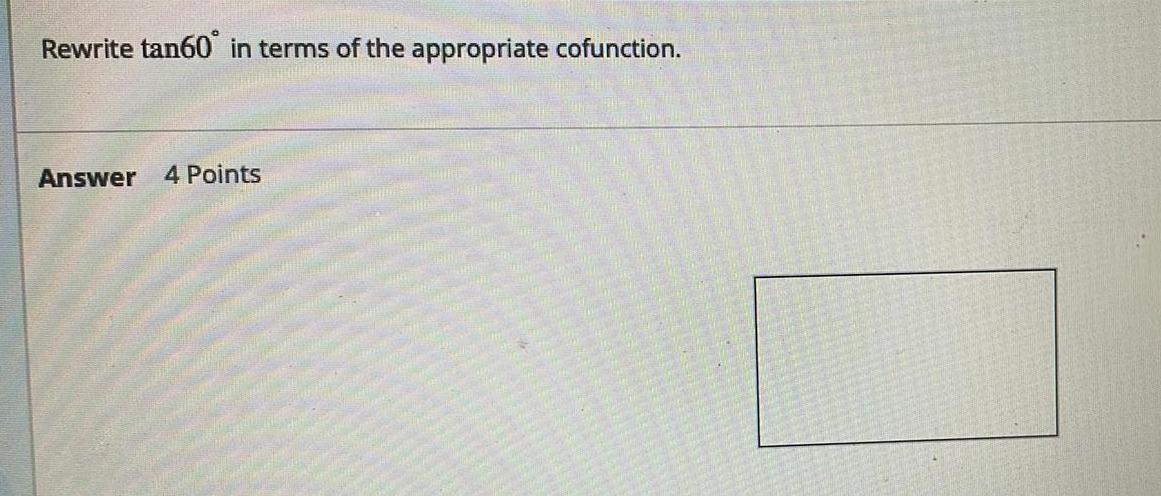
Trigonometry Questions and Answers

Math - Others
TrigonometryWhich one of the following is not a Pythagorean identity?
a) They are all Pythagorean identities
b) 1- cot² (θ) = csc²(θ)
c) tan² (θ) + 1 = sec² (θ )
d) sin² (θ ) + cos² (θ ) = 1

Math - Others
TrigonometryFor the function f(x) = -2 cos (3x - π/2) -1, the phase shift is:
a) π/2 units to the right
b) π/2 units to the left
c) π/6 units to the right
d) 3π/2 units to the right
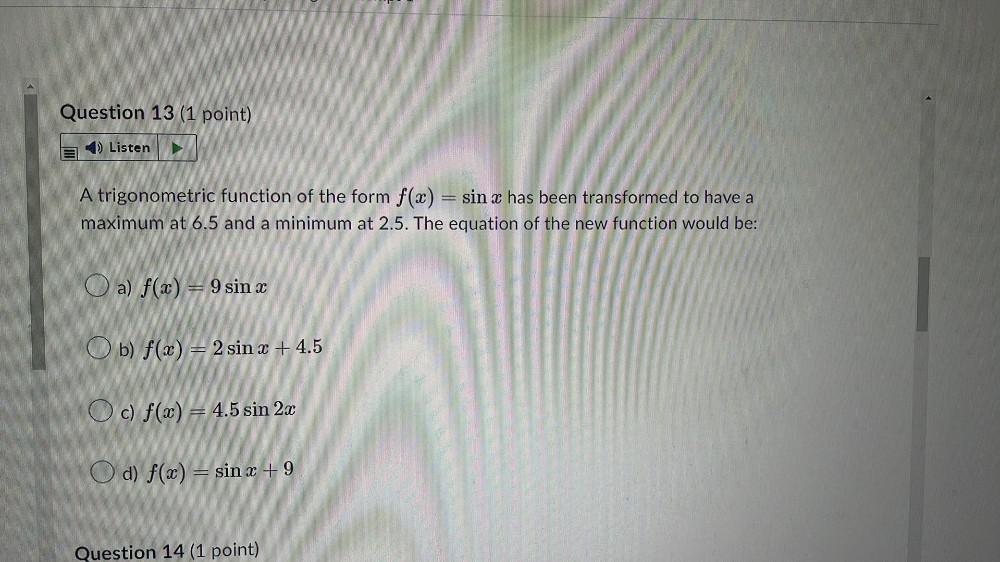
Math - Others
TrigonometryA trigonometric function of the form f(x) = sin x has been transformed to have a
maximum at 6.5 and a minimum at 2.5. The equation of the new function would be:
a) f(x) = 9 sin x
b) f(x) = 2 sin x + 4.5
c) f(x) = 4.5 sin 2x
d) f(x) = sin x + 9
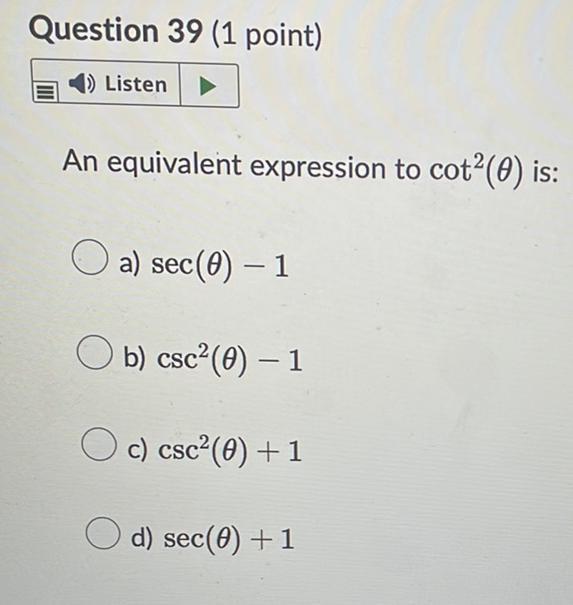
Math - Others
TrigonometryAn equivalent expression to cot²(θ) is:
a) sec(θ) - 1
b) csc²(θ) - 1
c) csc²(θ)+1
d) sec(θ) + 1

Math - Others
TrigonometryA sine function is reflected in the x-axis and the y-axis. A possible function is:
a) f(x) = -sin x
b) f(x) = sin x – 1
c) f(x) = -sin(-x)
d) f(x) = sin(-x)

Math - Others
TrigonometryThe trigonometric functions have a period of 2π radians. This statement is:
a) true for both the sine and cosine functions
b) true only for the sine function
c) true for all three basic trigonometric functions
d) true only for the cosine function
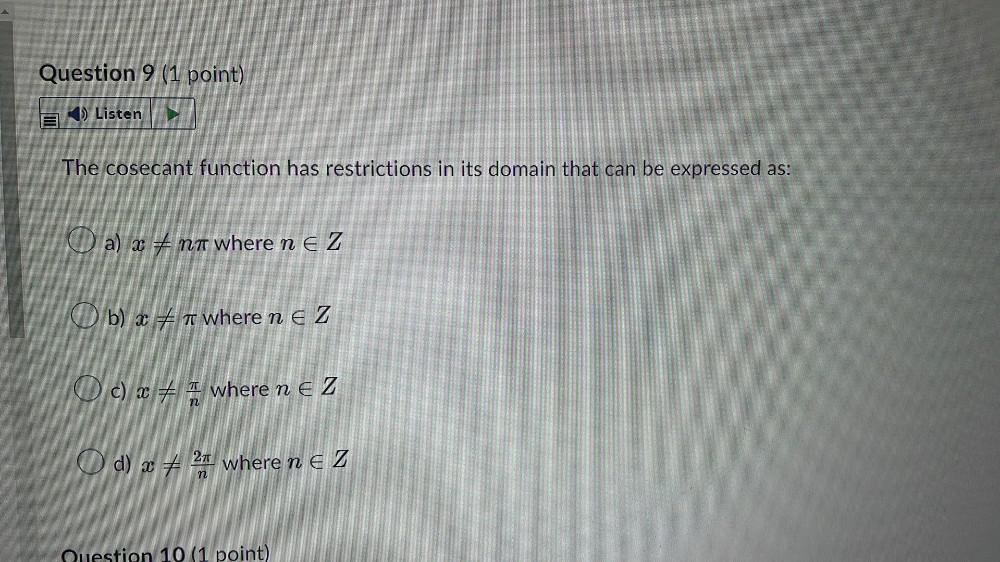
Math - Others
TrigonometryThe cosecant function has restrictions in its domain that can be expressed as:
a) x ≠ nπ where n ∈ Z
b) x ≠ π where n ∈ Z
c) x ≠ π/n where n ∈ Z
d) x ≠ 2 π/n where n ∈ Z
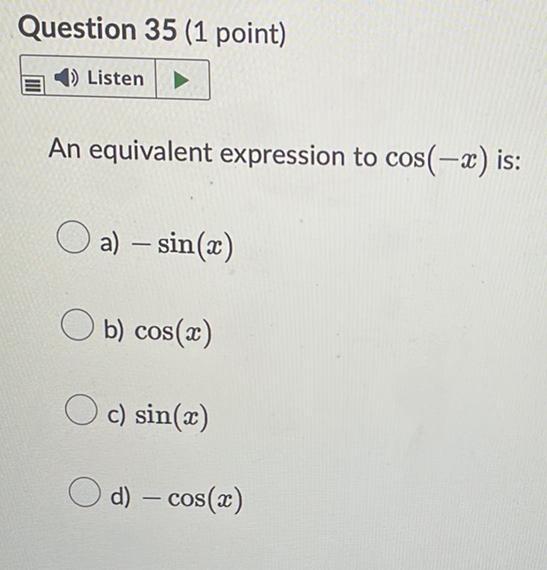
Math - Others
TrigonometryAn equivalent expression to cos(-x) is:
a) - sin(x)
b) cos(x)
c) sin(x)
d) - cos(x)
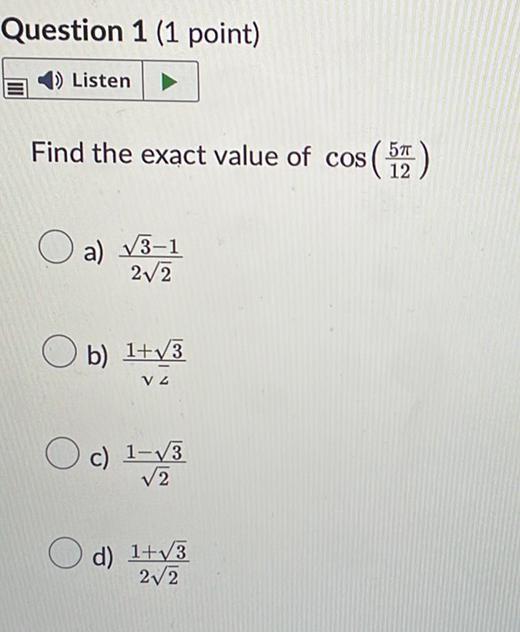
Math - Others
TrigonometryFind the exact value of cos (5π/12)
a) √3-1/2√2
b) 1+√3/√2
c) 1-√3/√2
d) 1+√3/2√/2
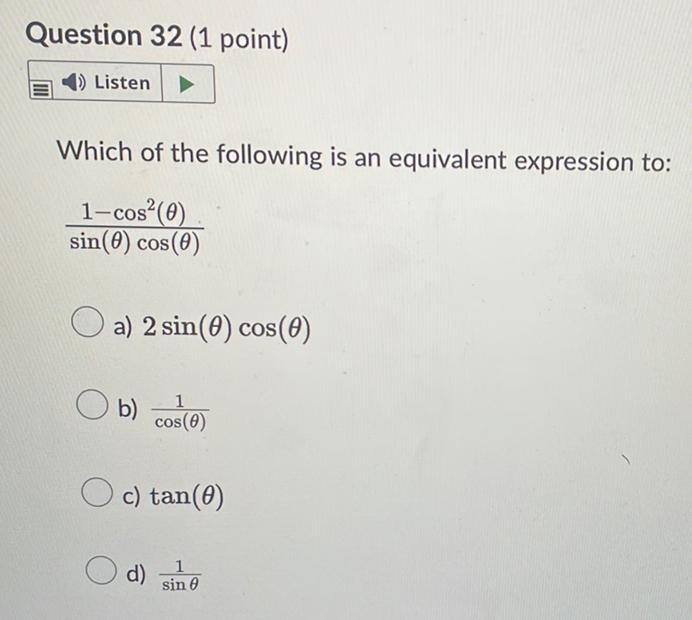
Math - Others
TrigonometryWhich of the following is an equivalent expression to:
(1-cos²(θ))/(sin(θ) cos(θ))
a) 2 sin(θ) cos(θ)
b) 1/cos(θ)
c) tan (θ)
d) 1/sin θ
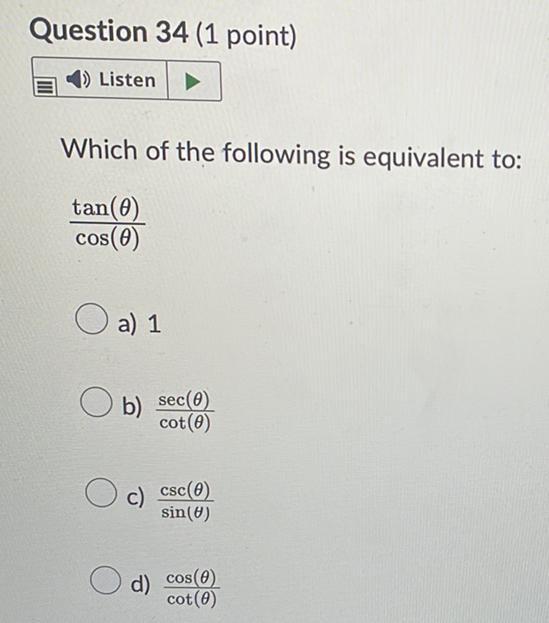
Math - Others
TrigonometryWhich of the following is equivalent to:
tan (θ)/cos(θ)
a) 1
b) sec(θ)/cot (0)
c) csc (θ)/sin(θ)
d) cos(θ)/cot (θ)
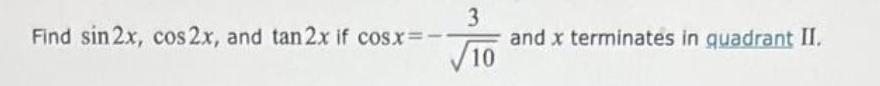
Math - Others
TrigonometryFind sin 2x, cos2x, and tan 2x if cosx=-3/√10 and x terminates in quadrant II.

Math - Others
TrigonometryFind the exact value of the expressions cos(α+ß), sin(α + ß) and tan(a +ß) under the following conditions:sin(α) =40/41, x lies in quadrant I, and sin(β) =12/13
ß lies in quadrant II.
a. cos(α+β)=
(Simplify your answer. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression.)
b. sin(α + β) =
(Simplify your answer. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression.)
c. tan(α + β) =
(Simplify your answer. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression.)
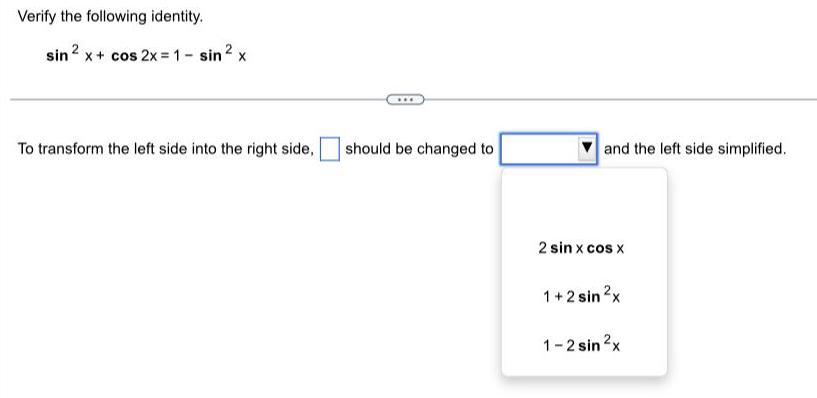
Math - Others
TrigonometryVerify the following identity. sin ² x + cos2x = 1 - sin ² x
To transform the left side into the right side, should be changed to___ and the left side simplified.

Math - Others
TrigonometryA point on the terminal side of an angle θ in standard position is given. Find the exact values of the six trigonometric functions of θ.
(-1/3,-1/4)
sin θ =
cos θ =
tan θ=
csc θ=
sec θ =
cot θ=

Math - Others
TrigonometryUsing the Law of Sines to solve the triangle if ∠A = 38°, ∠C = 72°, b = 20:
∠B is___degrees;
a=
c =
Round to two decimal places if needed.
Assume ∠A is opposite side a, ∠B is opposite side b, and ∠C is opposite side c.

Math - Others
TrigonometryExpress the given product as a sum or difference containing only sines or cosines.
sin (9x) sin (7x)

Math - Others
TrigonometryWhile working on a geometry problem, Raul determines that the angles of one triangle are congruent to the corresponding angles of another triangle. Which of the following is a valid deduction that Raul can make?
A) The two triangles are congruent but not necessarily similar.
B) The two triangles are similar but not necessarily congruent.
C) The two triangles are both similar and congruent.
D) The two triangles are neither similar nor congruent.

Math - Others
TrigonometryA triangle with side lengths of 5, 12, and 15 centimeters is similar to another triangle. The longest side of the other triangle has length 24 centimeters. What is the perimeter, in centimeters, of the larger triangle?

Math - Others
TrigonometryFind all EXACT solutions of the equation
cos(x) =-√2/2
in the interval [0,2x). If there is more than one answer, enter them in a list separated by commas. Enter an exact expression; decimal approximations or symbolic trigonometric expressions such as arctan (5) will be marked incorrect.

Math - Others
TrigonometryGraph the trigonometic function. y=-1/2 sin 2x. plot all points corresponding to x- intercepts, minima and maxima within one cycle.
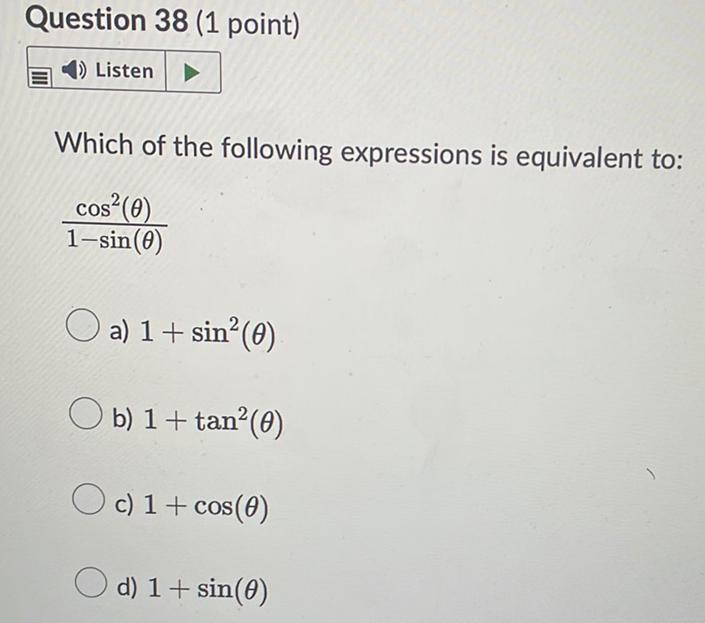
Math - Others
TrigonometryWhich of the following expressions is equivalent to: cos² (θ ) / 1-sin (θ)
a) 1+ sin²(θ )
b) 1 + tan² (θ )
c) 1 + cos (θ)
d) 1+ sin(θ)
![Find all values of 0 and all values of 0 in [0, 2π] for the equation given below. Be sure to the algebra or trigonometry you use and give exact values to ensure full credit.
sin (3x) =√3/2](https://media.kunduz.com/media/sug-question/raw/84695487-1658951776.77069.jpeg?w=256)
Math - Others
TrigonometryFind all values of 0 and all values of 0 in [0, 2π] for the equation given below. Be sure to the algebra or trigonometry you use and give exact values to ensure full credit.
sin (3x) =√3/2

Math - Others
TrigonometrySolve the following equation on the interval
[0°, 360°). Separate multiple answers with a comma. Remember to include a degree symbol.
4cos²x sinx - sinx = 0
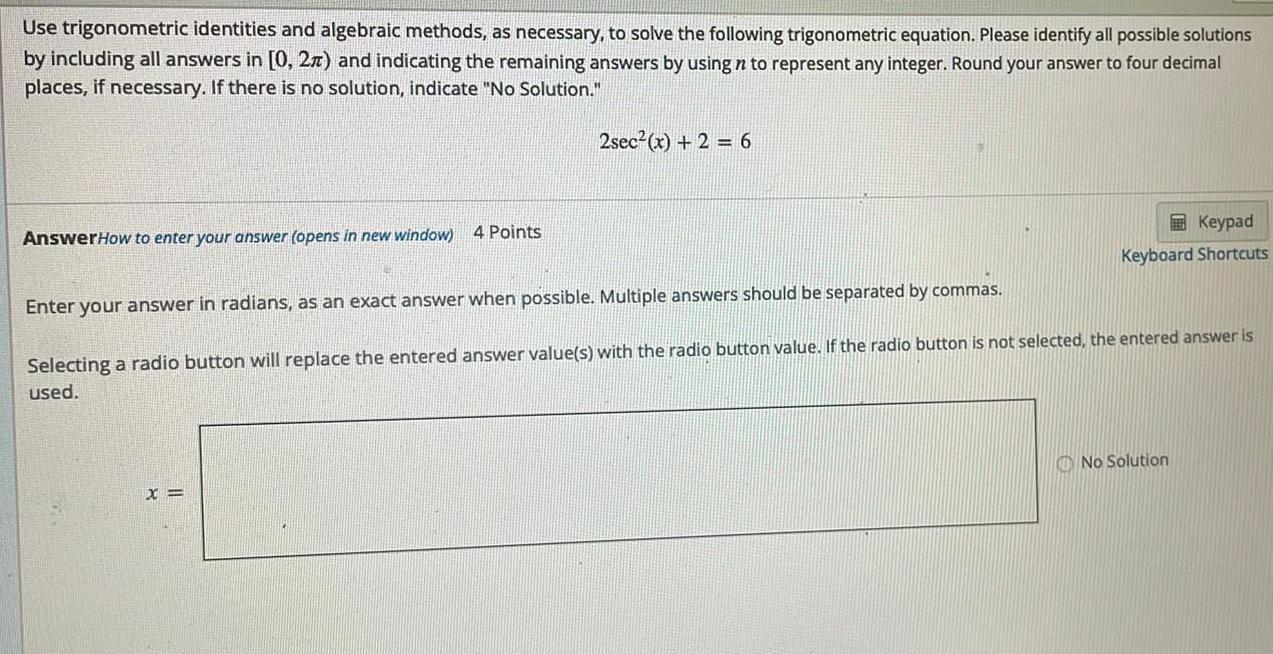
Math - Others
TrigonometryUse trigonometric identities and algebraic methods, as necessary, to solve the following trigonometric equation. Please identify all possible solutions by including all answers in [0, 2π) and indicating the remaining answers by using n to represent any integer. Round your answer to four decimal places, if necessary. If there is no solution, indicate "No Solution." 2sec²(x) + 2 = 6

Math - Others
TrigonometryLet F= {f|f: R→ R} denote the vector space of real-valued functions.
Which of the following are linearly independent subsets in F?
S = {sin x, cos x}
T = {1, sin x, cos x}
U = {1, sin² x, cos²x}
V = {1,2 sin² x, 3 cos² x}
mark (X) the correct answer:
A S and T
BS and U
CS and V
DT and U
ET and V
FU and V
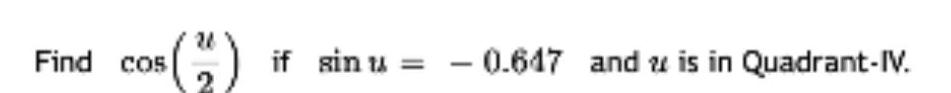

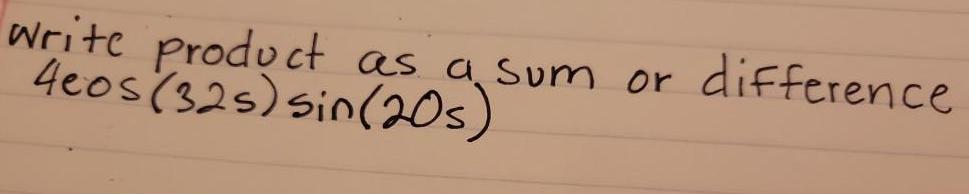


Math - Others
TrigonometrySolve 3 sin 2 (w)-13 sin(w) + 4 = 0 for all solutions OLW LIT W = Give answer accurate to 2 decimal Places, as a list seperated by commas.



Math - Others
TrigonometryTwo straight roads diverge at an angle of 45°. Two cars leave the intersection at 2:00 P.M., one traveling at 42 mi/h and the other at 38 mi/h. How far apart are the cars at 2:30 P.M.? (Round your answer to two decimal places.)
Math - Others
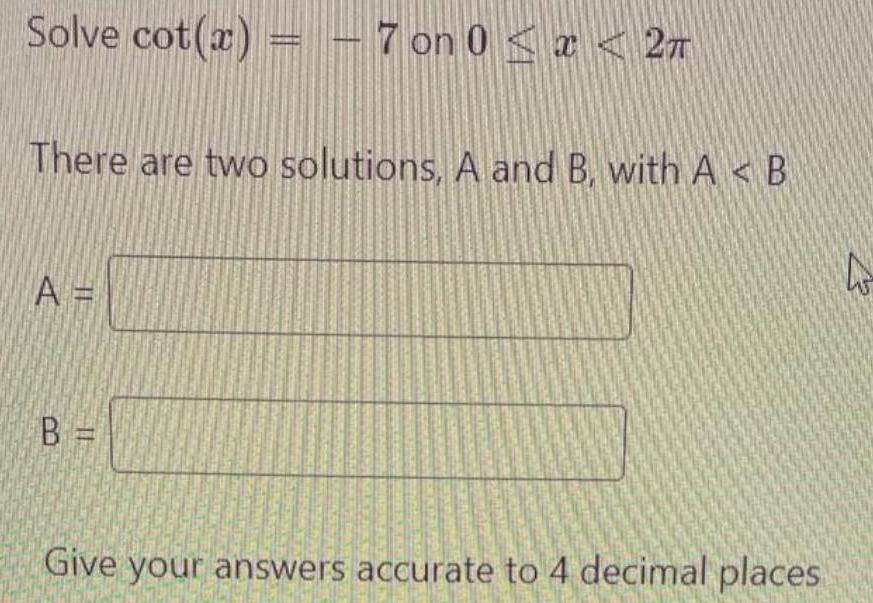
TrigonometrySolve cot(x) = - 7 on 0 ≤ x < 2π
There are two solutions, A and B, with A B
A =
B =
Give your answers accurate to 4 decimal places

Math - Others
TrigonometryEvaluate and round to the forth number after the decimal point.
sin 74⁰
cos 48⁰
tan 38⁰
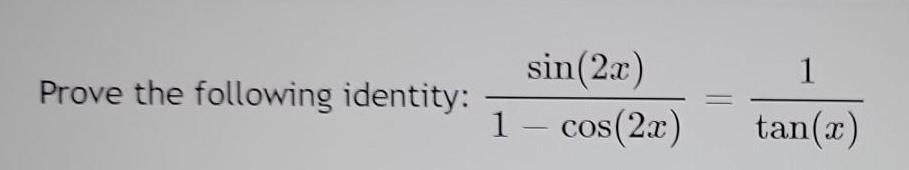



Math - Others
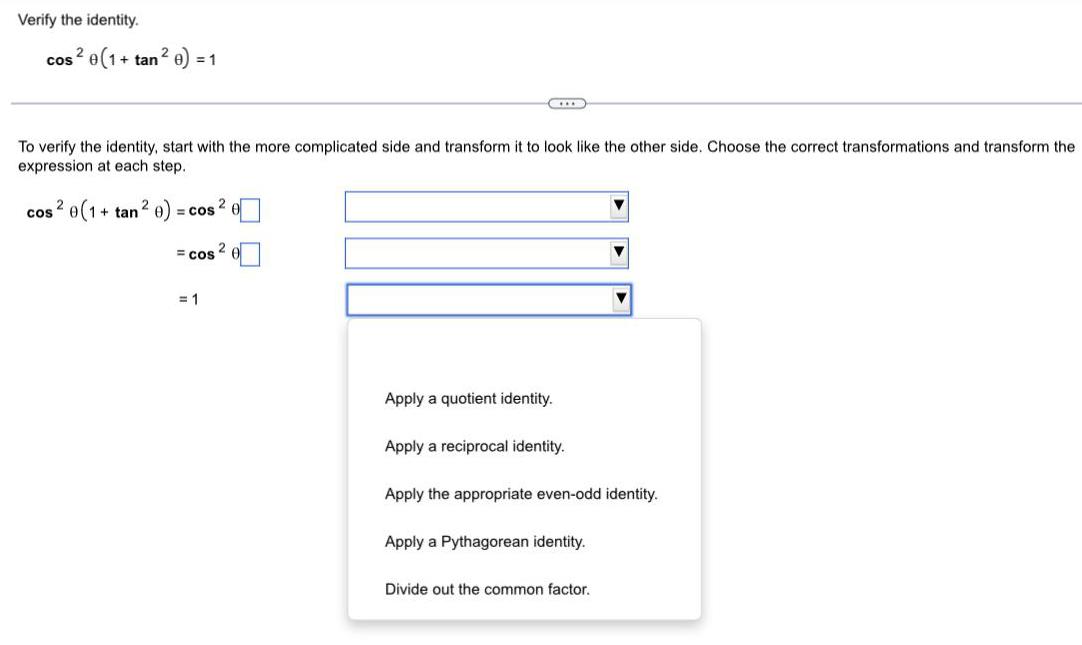
TrigonometryVerify the identity.
cos² 0(1+ tan² e) = 1
To verify the identity, start with the more complicated side and transform it to look like the other side. Choose the correct transformations and transform the
expression at each step.

Math - Others
TrigonometryA hot-air balloon is rising vertically. The angle of elevation from a point on level ground 123 feet from the balloon to a point directly under the passenger compartment changes from 18° to 33.2°. How far, to the nearest tenth of a foot, does the balloon rise during this period? 180 123 ft 33.20
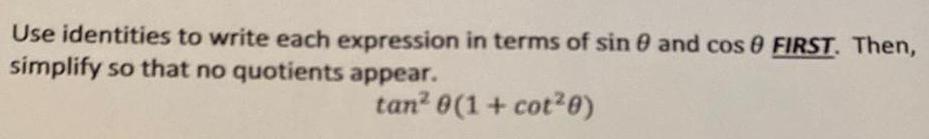
Math - Others
TrigonometryUse identities to write each expression in terms of sin θ and cosθ FIRST. Then, simplify so that no quotients appear. tan²θ (1+ cot²θ)
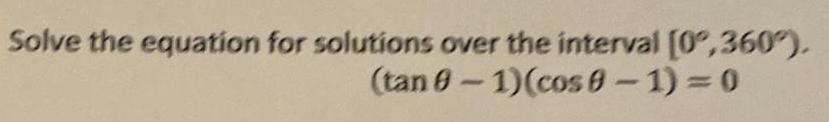
Math - Others
TrigonometrySolve the equation for solutions over the interval [0°,360). (tan θ-1)(cosθ-1) = 0


Math - Others
TrigonometryThe hypotenuse of a right triangle is 3 less than twice the shorter leg. The length of the other leg is 3 more than the shorter leg. Find the length of the shorter leg.

Math - Others
TrigonometryAn airplane is sighted at the same time by two ground observers who are 3 miles apart and both directly west of the airplane. They report the angles of elevation as 14° and 25°. How high is the airplane?

Math - Others
TrigonometrySolve the equation on the interval [0, 2π).
sin 2x + sin x = 0
0,2π/3,π,4π/3
π/4,3π/4,5π/4,7π/4
π/8,9π/8
no solution