Trigonometry Questions and Answers

Math - Others
TrigonometryGraph the function and y = cos x in the same rectangular system for 0 ≤ x ≤ 2π
y = 3 cos x
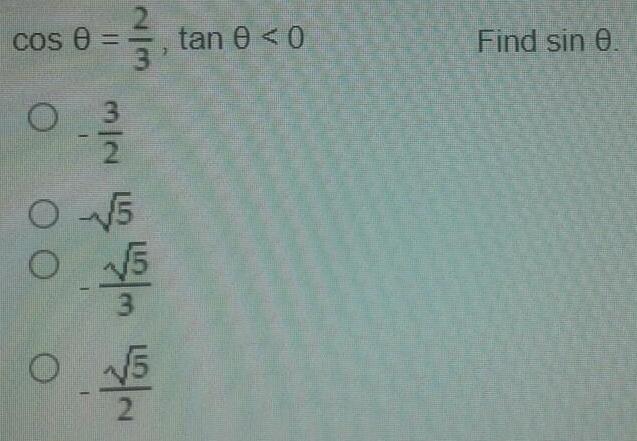

Math - Others
Trigonometrycos x + sinx/cosx - sinx-cos/sinx
sec x csc X
2 + sec x csc X
1 - sec x csc X
2 - sec x csc X

Math - Others
TrigonometryComplete the identity.
sin^2 x + tan^2x + cos^2x = ?
sec² x
tan² x
cot³x
sin x

Math - Others
TrigonometrySolve the equation on the interval [0, 2π).
cos^ 2 x + 2 cos x + 1 = 0
π /2 ,3π/7
π
π/4,7π/4
2π

Math - Others
TrigonometryFrom the professor's perspective, explain the pros and cons of using the method below in finding trigonometric values of special angles. Then present an example to illustrate the process.
(a) reference angle method
(b) unit circle method

Math - Others
TrigonometrySolve for the exact solutions in the interval [0, 2π) . Separate solutions with a comma. If the equation has no solutions, respond with DNE.
sin(4x) = 1/ 2
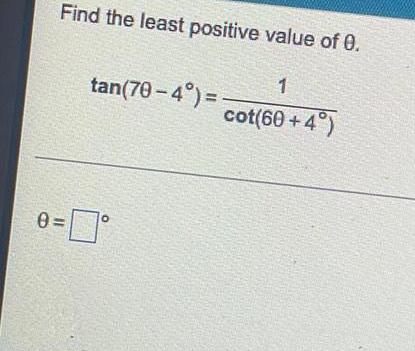
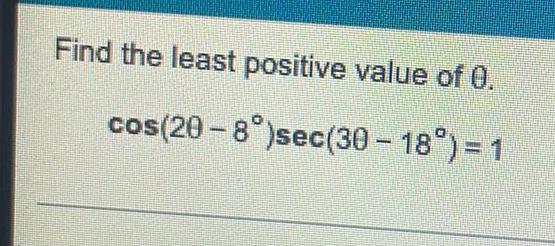
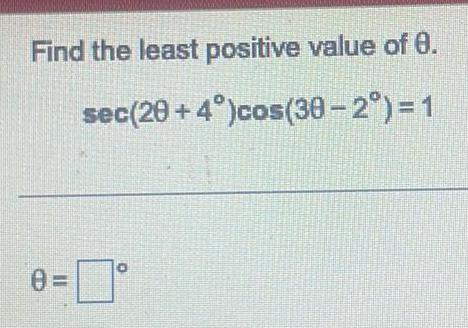
![Find a value of a in [0°, 90°] that satisfies the given statement.
csc a= 1.2763014](https://media.kunduz.com/media/sug-question/raw/84589234-1658517657.7403128.jpeg?w=256)
Math - Others
TrigonometryFind a value of a in [0°, 90°] that satisfies the given statement.
csc a= 1.2763014
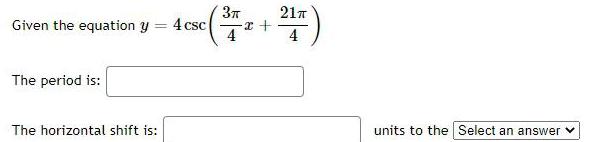
Math - Others
TrigonometryGiven the equation y=4 csc(3π/4 x + 21π/x)
The period is:
The horizontal shift is:__units to the Select an answer
Math - Others
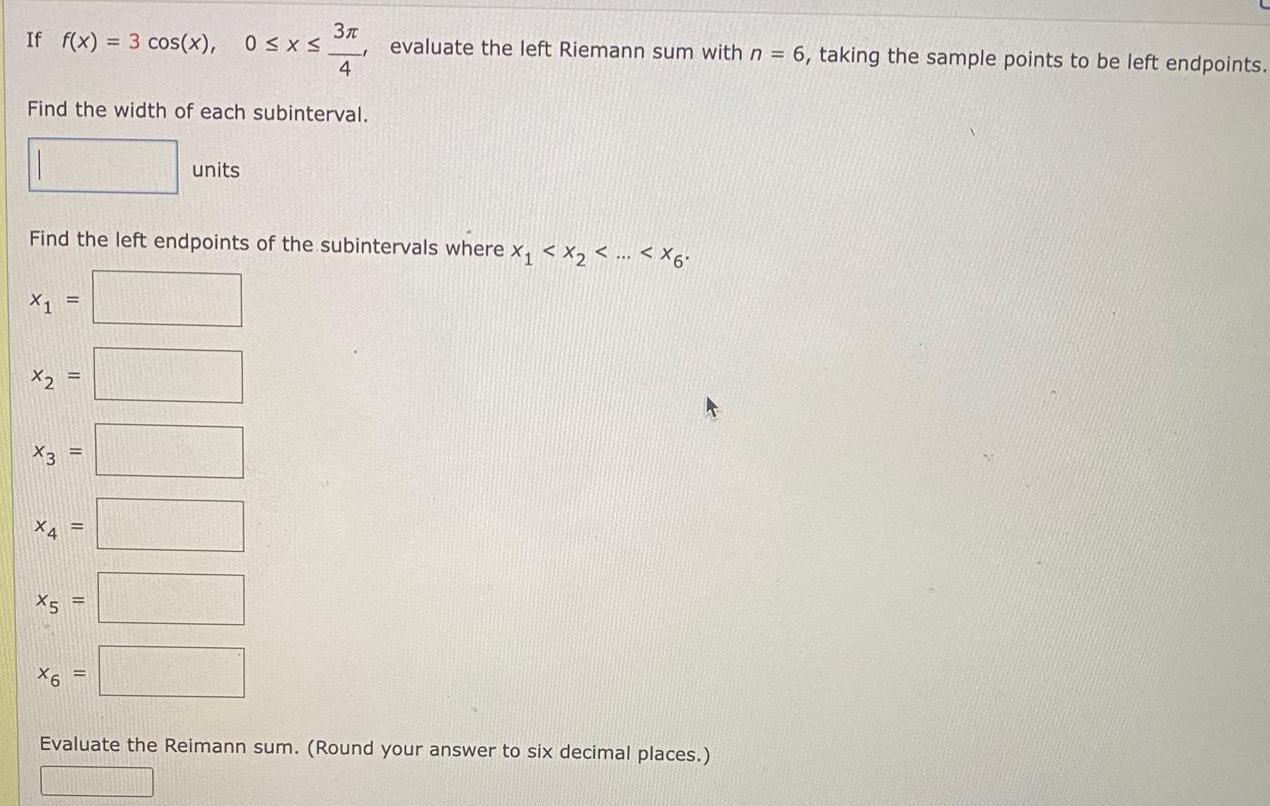
TrigonometryIf f(x) = 3 cos(x), 0≤x≤3π/4
Find the width of each subinterval.
Find the left endpoints of the subintervals where x₁ < x2 <......... < X6.
x1
x2
x3
X4
X5
X6
evaluate the left Riemann sum with n = 6, taking the sample points to be left endpoints.
Evaluate the Reimann sum. (Round your answer to six decimal places.)

Math - Others
TrigonometryEvaluate sin (cos-¹(x/8)).
√64-x²/8
8/√64-x^2
√x²-64/8
8/√x²-64
None of These

Math - Others
TrigonometryFind linear approximation of the given quantity:
sin 122° Round your answer to 4 d.p.

Math - Others
TrigonometryGraph on period of y = -tan(-1/4x+π/8) centered at the phase shift, including all roots and asymptotes -The standard form y = -tan(-1/4(x-(-π/2))

Math - Others
TrigonometryGiven that cos A =-4/5 with angle A in quadrant II and sin B = -24 /25 with angle B in quadrant III. Find cos(A + B)
none of these
3/5
4/5
-4/5
-3/5

Math - Others
TrigonometryChoose 1 of the 2 trigonometric equations below to solve for x. Express your answer(s) in the interval [0, 2x)
a. cos(2x)-cosx=0
b. 4tan^2 x + 4tanx=0
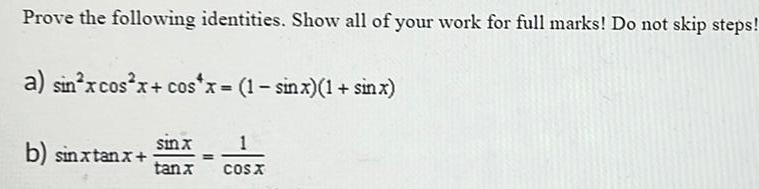
Math - Others
TrigonometryProve the following identities. Show all of your work for full marks! Do not skip steps!
a) sin²xcos²x+cos4x = (1-sinx)(1+ sin x)
b) sinxtanx+ sinx tanx = 1 cosx

Math - Others
TrigonometryThe distance from the Sun to Earth is approximately 149600000 km. Assuming Earth has a circular* orbit around the Sun, find the distance Earth travels in orbiting the Sun through an angle of 3.64 radians.
*Be it noted that the planets orbiting the Sun actually have elliptical orbits, not circular.
544650100 km
544664000 km
544688575 km
544544000 km
None of the above
Math - Others
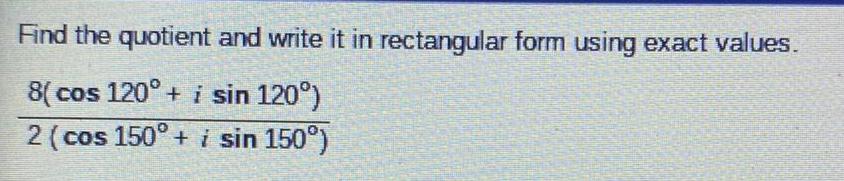
TrigonometryFind the quotient and write it in rectangular form using exact values.
8( cos 120° + i sin 120°)
2 (cos 150° + i sin 150°)

Math - Others
TrigonometryAirports A and B are 444 km apart, on an east-west line. Jim flies in a northeast direction from A to airport C. From C he flies 347 km on a bearing of 125°50' to B. How far is C from A?

Math - Others
TrigonometryA triangular swimming pool measures 46 ft on one side and 32.8 ft on another side. The two sides form an angle that measures 41.3°. How long is the third side?

Math - Others
TrigonometryWrite the complex number in rectangular form.
7 cis 315°
The complex number is

Math - Others
TrigonometryDetermine the number of triangles ABC possible with the given parts.
A 39.8° a 3.5 c= 8.4
How many possible solutions does this triangle have?

Math - Others
TrigonometryA triangular swimming pool measures 42 ft on one side and 32.8 ft on another side. The two sides form an angle that measures 40.6°. How long is the third side?


Math - Others
TrigonometrySimplify sin(π – u) to a single trig function using a sum or difference of angles identity.
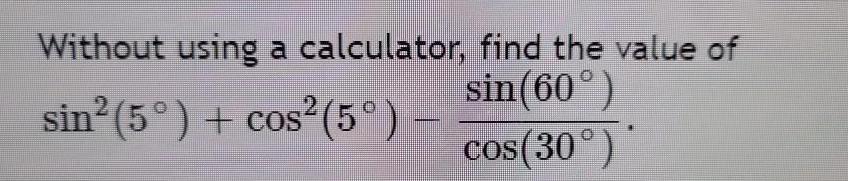
Math - Others
TrigonometryWithout using a calculator, find the value of
sin² (5°) + cos² (5°) - sin(60°)/cos(30°)
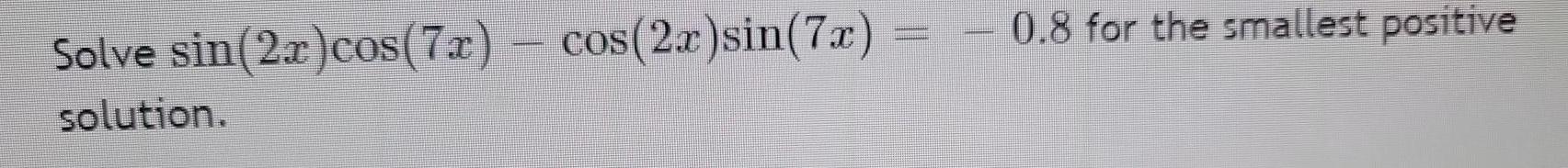
Math - Others
TrigonometrySolve sin(2x)cos(7x) – cos(2x)sin(7x)=-0.8 for the smallest positive solution.
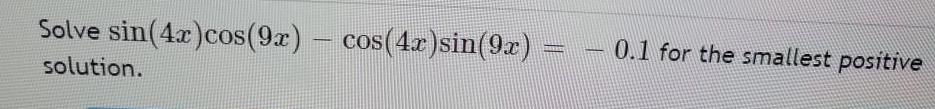
Math - Others
TrigonometrySolve sin(4x) cos(9x) - cos(4x) sin(9x) = - 0.1 for the smallest positive solution
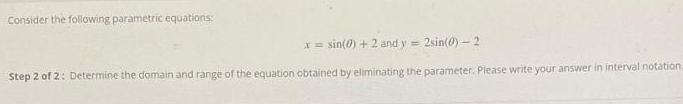
Math - Others
TrigonometryConsider the following parametric equations:
x = sin(θ) + 2 and y= 2sin(θ)-2
Step 2 of 2: Determine the domain and range of the equation obtained by eliminating the parameter. Please write your answer in interval notation.

Math - Others
TrigonometrySimplify sin(t)sec(t) to a single trig function or constant with no fractions.


Math - Others
TrigonometrySimplify sin² (t)/1-sin² (t) to an expression involving a single trig function with no
fractions.
If needed, enter squared trigonometric expressions using the following
notation.
Example: Enter sin² (t) as (sin(t))².
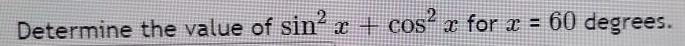
Math - Others
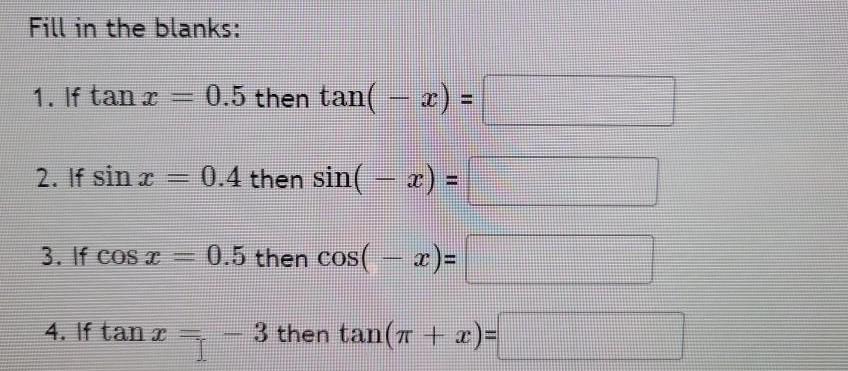
TrigonometryFill in the blanks:
1. If tan x = 0.5 then tan( − x) =
2. If sin x = 0.4 then sin( -x) c=
3. If cos x = 0.5 then cos( x ) =
4. If tan x = -3 then tan(π + x) =

Math - Others
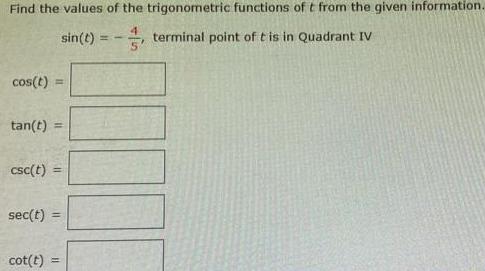
TrigonometryFind the values of the trigonometric functions of t from the given information. sin(t) = 4/5, terminal point of t is in Quadrant IV
cos(t) =
tan(t) =
csc(t) =
sec(t)
cot(t):


Math - Others
TrigonometryA student solved this question: Find the value(s) of x within 0 ≤ x ≤ 2π for the following
expression sin² (2x) + = = 2sin(x) cos(x).
Did they make any mistakes in their work below? If yes, show where the mistakes are by explaining what they did wrong. Then fix the problem to get the correct answer based on the question.

Math - Others
TrigonometryUse the sum or difference formula for tangent to find the exact value for tan(-75°)
tan(-75°)

Math - Others
TrigonometryThe point of concurrency of the perpendicular bisectors of a triangle is called the
centroid.
incenter.
orthocenter.
circumcenter.


Math - Others
TrigonometryDetermine the quadrant when the terminal side of the angle lies according to the following conditions: sin (t) > 0, tan (t) <0.
Quadrant I
Quadrant III
Quadrant IV
Quadrant II

Math - Others
TrigonometryFind the value of the trigonometric function sin (t) if sect=-4/3 and the terminal side of angle t lies in quadrant II.
sin (t) = 3/4
sin (t) =√5/4
sin (t) = 5/4
sin (t) = √7/4

Math - Others
TrigonometryFor 0 < θ<π/2, find the values of the trigonometric functions based on the given one (give your answers with THREE DECIMAL PLACES or as expressions, e.g. you can enter 3/5).
If cos(θ) = 5/11 then
sin(θ) =
sec(θ) =
csc (θ) =
tan(θ) =
cot(θ) =

Math - Others
TrigonometryFind a positive angle less than one revolution around the unit circle that is co-terminal with the given angle: 52π/5
8π/5
12π/5
5π/2
2π/5
Math - Others
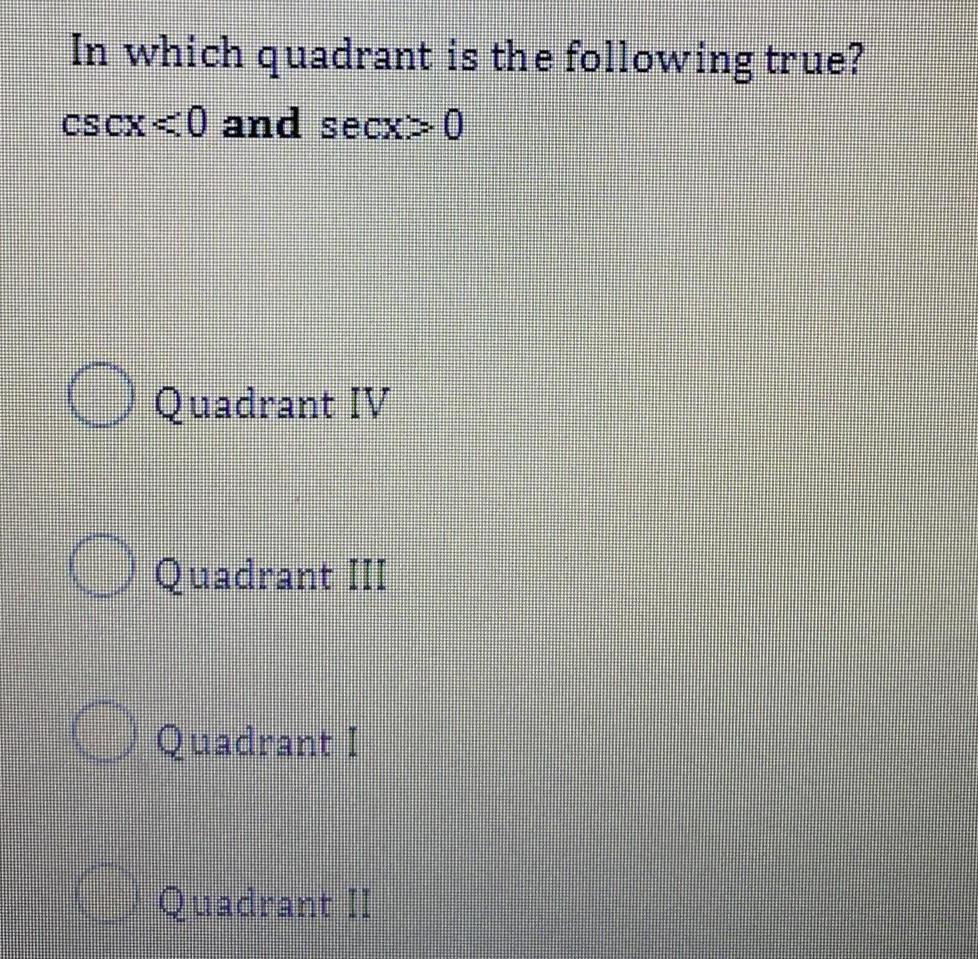
TrigonometryIn which quadrant is the following true?
cscx<0 and secx>0
Quadrant IV
Quadrant III
Quadrant I
Quadrant II

Math - Others
TrigonometryFor an angle A in standard position, if sinA=cosA then the terminal arm of the angle
lies in quadrants II or IV.
True
False