Fonksiyon Türleri Nelerdir?
- Bire Bir Fonksiyon
- Örten Fonksiyon
- Birebir Örten Fonksiyon
- İçine Fonksiyon
- Birim Fonksiyon
- Bileşke Fonksiyon
- Sabit Fonksiyon
- Sıfır Fonksiyon
- Doğrusal Fonksiyon
- Ters Fonksiyon
- Parçalı Fonksiyon
- Tek Fonksiyon
- Çift Fonksiyon
- Eşit Fonksiyonlar
- Periyodik Fonksiyon
Bire Bir Fonksiyon
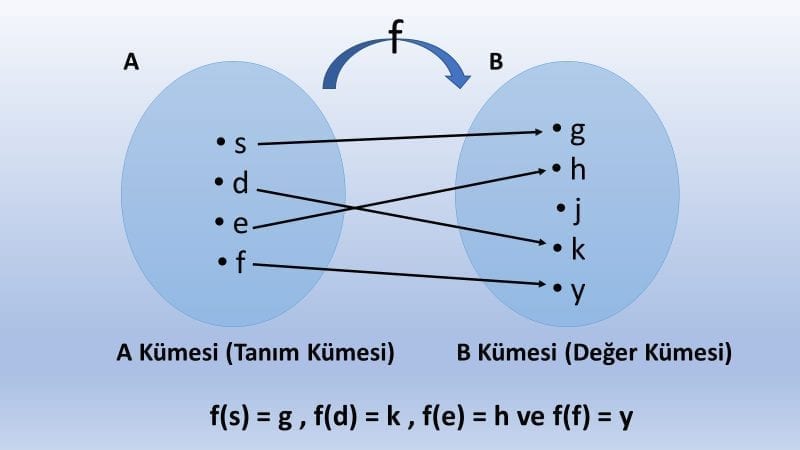
Bir fonksiyonun tanım kümesinden alınan her bir elemanın görüntüsü diğer elemanların görüntülerinden farklı ise o fonksiyona bire bir fonksiyon denir.
Kural olarak göstermemiz gerekirse: ∀ a,b ∈ A için, f(a) = f(b) iken, a = b oluyorsa f fonksiyonu bire birdir.
Verilen fonksiyon grafiğinden o fonksiyonun bire bir olup olmadığını anlamak için yatay doğru testi uygulanır. Analitik düzlemde x ekseninde paralel doğrular çizildiğinde bu doğrular fonksiyonun grafiğini tek noktada kesiyorsa fonksiyon bire birdir. Eğer bu doğrular grafiği birden fazla noktada kesiyorsa fonksiyon bire bir değildir.
Örten Fonksiyon
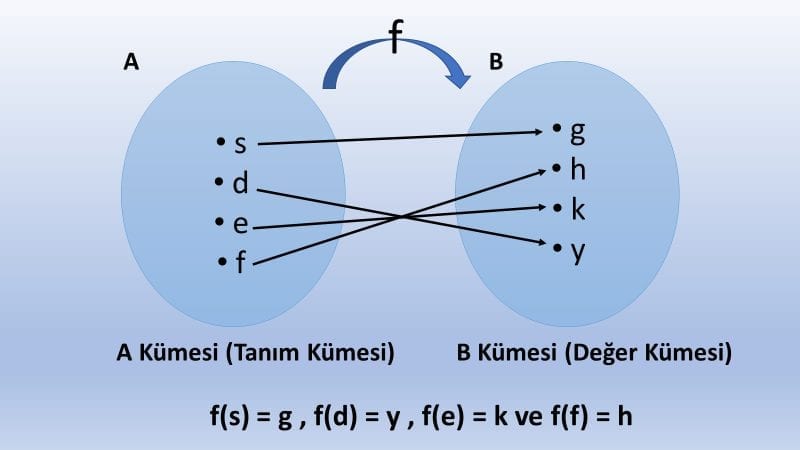
Bir fonksiyonun değer kümesindeki her eleman tanım kümesinden en az bir elemanla eşleşmiş ise bu fonksiyona örten fonksiyon denir.
Görüntü kümesiyle değer kümesinin aynı olduğu fonksiyonlara örten fonksiyon deniyor, yani B kümemizde eşi olmayan eleman olmaması gerekiyor. Hem A kümesindeki her elamanın B de özel bir eşi var, hem de B kümesindeki her eleman A kümesinde bir eşe sahip. Bu yüzden fonksiyonumuz hem bire bir hem de örtendir.
Verilen fonksiyon grafiğinden o fonksiyonun örten olup olmadığını anlamak için yatay doğru testi uygulanır. Analitik düzlemde x ekseninde paralel olarak çizilen tüm doğrular fonksiyonu en az bir noktada kesiyorsa fonksiyon örtendir.
İpucu: Örten değilse içine fonksiyon olduğunu söyleyebiliriz.
Bire Bir Örten Fonksiyon
Bire bir örten fonksiyon, matematikte hem bire bir hem örten fonksiyon özelliklerini aynı anda gösteren fonksiyonlardır. İki küme arasındaki fonksiyonda 1. kümeden her bir eleman ikinci kümedeki elemanla eşleşir ve her iki kümeden açıkta eleman kalmaz.
Örten fonksiyon görüntü kümesinde boşta eleman kalmayacak şekilde eşleşmenin gerçekleştiği, birebir fonksiyon ise her bir elemanın diğer kümenin bir elemanıyla eşleştiği fonksiyondur.
Bire bir örten fonksiyonlar ise bu iki fonksiyonun özelliklerine aynı anda sahip olan fonksiyonlardır. Bire bir örten fonksiyonlar terslenebilir özelliktedir ve bu tip fonksiyonlara permütasyon ismi verilir.
İçine Fonksiyon
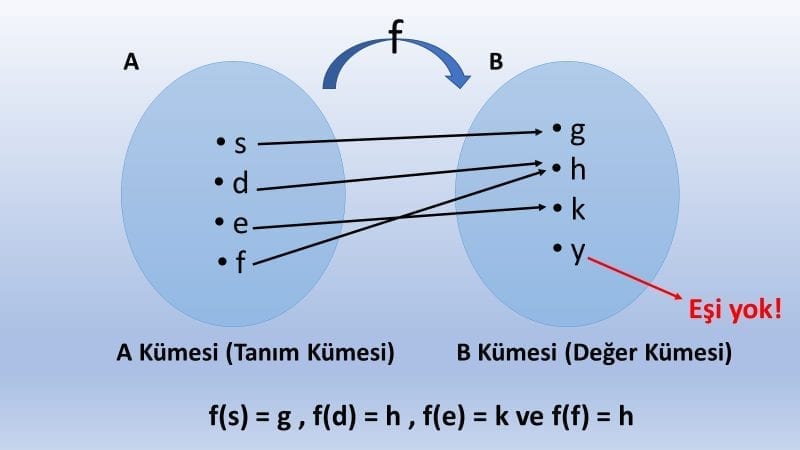
Bir fonksiyonun değer kümesinde tanım kümesindeki bir elemanla eşleşmemiş en az bir eleman bulunuyorsa bu fonksiyona içine fonksiyon denir.
Değer kümesinde, yani B kümesinde, eşi olmayan eleman varsa bu fonksiyona içine fonksiyon deriz.
Birim Fonksiyon
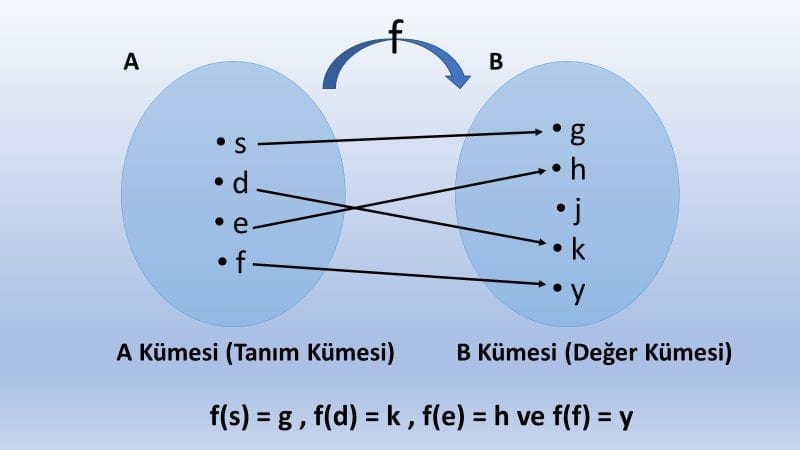
Tanım ve değer kümeleri aynı olan fonksiyonlarda her elemanı kendisine eşleyen fonksiyona birim fonksiyon denir.
A kümesi boş kümeden farklı olmak üzere, f: A → A fonksiyonunda her x ∈ A için f(x) = x ise bu f fonksiyonuna birim fonksiyon denir.
Birim fonksiyonu tanım ve değer kümelerinin şemasıyla gösterelim.
Bileşke Fonksiyon
A,B,C boş olmayan kümeler olmak üzere;
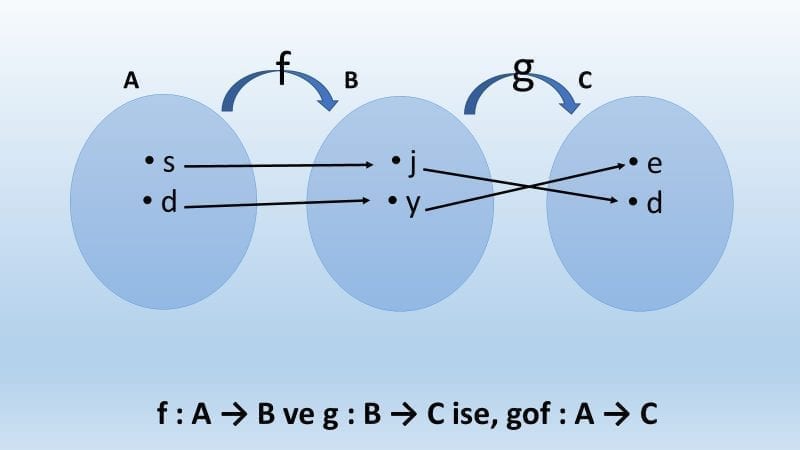
f : A → B ve g : B → C olmak üzere
A’dan C’ye tanımlanabilecek h : A → C fonksiyonunu f ile g fonksiyonlarının bileşkesidir.
A,B,C boş olamayan kümeler olmak üzere;
A’dan C’ye tanımlanan h : A → C fonksiyonuna “g bileşke f” fonksiyonu denir ve
h : gof(x) = g(f(x)) şeklinde gösterilir.
Örnek:
f : R → R ve f(x) = 2x + 5
g : R → R ve g(x) = 3x – 1 fonksiyonları verilmiştir. Bu durumda fog(x) fonksiyonu ne olur?
fog(x) = f(g(x)) = f(3x-1) = 2(3x-1) + 5 = (6x-2) + 5 = 6x + 3
fog(x) = 6x + 3 tür.
Sabit Fonksiyon
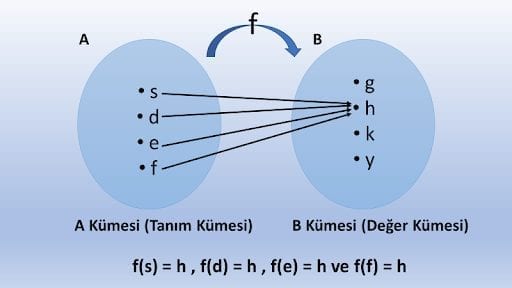
Tanım kümesindeki tüm elemanları değer kümesinde tek bir elemana eşleyen fonksiyona sabit fonksiyon denir.
∀x ∈ A ve c ∈ B için, f : A → B f(x) = c şeklinde tanımlanır. Buradaki “c” değeri sabit bir değeri ifade eder.
Sıfır Fonksiyon
f(x) = 0 fonksiyonuna sıfır fonksiyon denir.
∀x ∈ A ve 0 ∈ B için, f : A → B f(x) = 0 şeklinde tanımlanır.
Doğrusal Fonksiyon
a, b reel sayı olmak üzere, f : R → R, f(x) = ax + b şeklindeki fonksiyonlara doğrusal fonksiyon denir.
Ters Fonksiyon
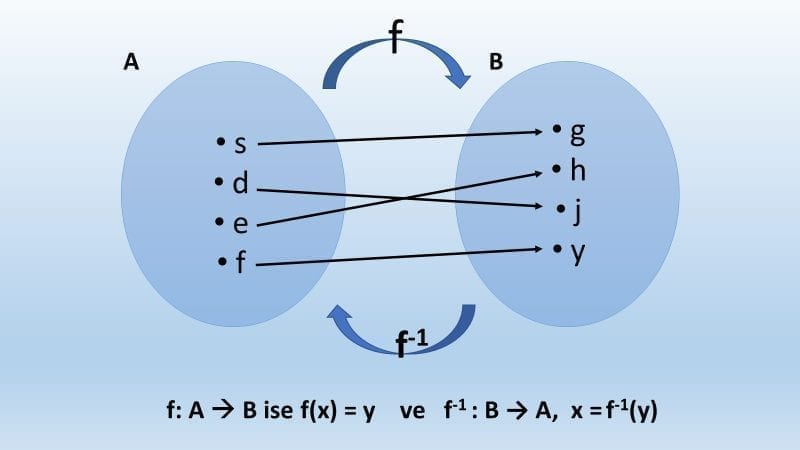
Ters fonksiyon, bir fonksiyonun görüntü kümesinden alınan herhangi bir elemanını tanım kümesinden asıl haline gönderen fonksiyona denir.
Bir fonksiyonun tersi bulunurken öncelikle fonksiyonda y = f(x) olarak yazılıp x yalnız bırakılır. Daha sonra y gördüğümüz yere x ve x gördüğümüz yere de f^{-1} (x) yazılır.
Ters fonksiyon ile ilgili daha fazla bilgi öğrenmek için buradan blog yazımızı inceleyebilirsin.
Parçalı Fonksiyon
Tanım kümesinin farklı aralıklarında farklı tanımlara sahip fonksiyonlara parçalı fonksiyon denir.
Tek Fonksiyon
f : A→B olmak üzere, her x ∈ A için;
f(-x) = -f(x) ise f fonksiyonu tek fonksiyondur.
Tek fonksiyonların grafikleri orijine göre simetriktir.
Örnek:
Örneğin; f(x)=2x³+x fonksiyonu için;
f(-2) = (-2)³ + (-2) = (-8) + (-2) = -10
f(2) = (2)³+2 = 8 + 2 = 10
f(-2) = -f(2)
f(x) fonksiyonu tek fonksiyondur.
Çift Fonksiyon
f : A→B olmak üzere, her x ∈ A için;
f(-x)=f(x) ise f fonksiyonu çift fonksiyondur.
Çift fonksiyonların grafikleri y eksenine göre simetriktir.
Örnek:
f(x)=x²+2x⁴+1 fonksiyonu için;
f(-2) = (-2)² + 2*(-2)⁴ +1 = 4 + 2*16 + 1 = 4 + 32 + 1 = 37
f(2) = (2)² + 2*(2)⁴ +1 = 4 + 2*16 + 1 = 4 + 32 + 1 = 37
f(-2) = f(2)
f(x) fonksiyonu çift fonksiyondur.
Eşit Fonksiyonlar
Tanım ve görüntü kümeleri birbiriyle aynı olan, tanım kümesindeki her bir elemanı için bu elemanların görüntüleri de aynı olan fonksiyonlara eşit fonksiyonlar denir.
Periyodik Fonksiyon
Aldığı değerler ve grafiği x ekseni boyunca düzenli aralıklarla kendini tekrarlayan fonksiyonlara periyodik fonksiyon denir.
Trigonometrik fonksiyonların tümü periyodiktir.
Örnek: Sinüs fonksiyonunun grafiği


